
D0:10.19721.cnki.1001-7372.2015.06.009 第28卷第6期 中国公路学报 Vol.28 No.6 2015年6月 China Journal of Highway and Transport June 2015 文章编号:100-7372(2015) 不同跨径桥梁车辆荷载分项系数及可靠度 杨晓艳,贡金盒1,冯云芬2 1.大连理工大学士木工程学院,辽宁大连116024:2.聊城大学建筑工程学院,山东聊城252059) 摘要:以可靠度理论和实测车辆荷载数据为基础,报学了考虑桥梁跨径对车辆荷载分项系数的影 响。根据近年中国车柄荷载实期数据,对不同跨径简支和连续桥梁的车辆荷载效应进行计算,建立 车柄益露被应的授率模型:控服相同超越概率的质则,得到不同路经桥粱车炳荷露放应玩准值的路 径影响系数,在此基础上确定了不同跨径桥梁结构的车辆荷载分项系数与跨径的关系,并采用一次 二阶矩可靠度方法计算了其可靠指标。结果表明:按相同超越概率原则确定的车辆荷载效应标准 值的跨径影响系数和车荷载分项系数随桥梁跨径的减小而增大:给出的考虑跨径影响的车柄荷 载分项系数计算公式更合理。 关键词:桥梁工程:荷我效应:概率模型:分项系数:可靠度 中图分类号:U441.2 文献标志码:A Partial Factors of Vehicle Loads and Reliability Analysis of Bridges with Different Spans YANG Xiao-yan',GONG Jin-xin',FENG Yumfen? Civil Engineering.Liaocheng University Liaocheng 52059. handong.China) Abstract:Based on reliability theory and recently measured vehicle load data.the influence of bridge span on partial factors of vehicle load was derived.According to recently vehicle load data measured in China,the vehicle load effects of multi-span simply supported and continuous two equ span bridges were as well as the probability models were founded.In acordance to the principle of the same exceeding probability,influence factors of span for characteristic values of vehicle load effects with various spans were obtained,based on which,the relationship between the partial factors of vehicle load effeets and the span of bridge was determined Reliability analysis for bridge design as per the determined vehicle load partial factor-span relationship was made with First-order Second-moment method (FOSM).The results show that the span influence factor and vehicle load partial factor for characteristic value of vehicle load effect,which were determined based on the equal exceeding probability,increase with the decrease of the span of bridge.The proposed span dependent partial factor calculation formula for vehicle load for bridge design is more reasonable. 日期.21402-12 21994-2019Ch al Electronic Publishing House.All rights reservec htp: www.cnki.ne
第28卷 第6期 2015年6月 中 国 公 路 学 报 ChinaJournalofHighwayandTransport Vol.28 No.6 June2015 文章编号:1001-7372(2015)06-0059-08 收稿日期:2014-07-17 基金项目:国家重点基础研究发展计划(“九七三”计划)项目(2015CB057703) 作者简介:杨晓艳(1985-),女,辽宁沈阳人,工学博士,E-mail:yangxiaoyan0024@126.com。 不同跨径桥梁车辆荷载分项系数及可靠度 杨晓艳1,贡金鑫1,冯云芬2 (1.大连理工大学 土木工程学院,辽宁 大连 116024;2.聊城大学 建筑工程学院,山东 聊城 252059) 摘要:以可靠度理论和实测车辆荷载数据为基础,推导了考虑桥梁跨径对车辆荷载分项系数的影 响。根据近年中国车辆荷载实测数据,对不同跨径简支和连续桥梁的车辆荷载效应进行计算,建立 车辆荷载效应的概率模型;按照相同超越概率的原则,得到不同跨径桥梁车辆荷载效应标准值的跨 径影响系数,在此基础上确定了不同跨径桥梁结构的车辆荷载分项系数与跨径的关系,并采用一次 二阶矩可靠度方法计算了其可靠指标。结果表明:按相同超越概率原则确定的车辆荷载效应标准 值的跨径影响系数和车辆荷载分项系数随桥梁跨径的减小而增大;给出的考虑跨径影响的车辆荷 载分项系数计算公式更合理。 关键词:桥梁工程;荷载效应;概率模型;分项系数;可靠度 中图分类号:U441.2 文献标志码:A PartialFactorsofVehicleLoadsandReliabilityAnalysisof BridgeswithDifferentSpans YANGXiao-yan1,GONGJin-xin1,FENGYun-fen2 (1.SchoolofCivilEngineering,DalianUniversityofTechnology,Dalian116024,Liaoning,China; 2.SchoolofArchitecture& CivilEngineering,LiaochengUniversity,Liaocheng252059,Shandong,China) Abstract:Basedonreliabilitytheoryandrecently measuredvehicleloaddata,theinfluenceof bridgespanonpartialfactorsofvehicleloadwasderived.Accordingtorecentlyvehicleloaddata measuredinChina,thevehicleloadeffectsofmulti-spansimplysupportedandcontinuoustwo- equalspanbridgeswerecalculated,aswellastheprobabilitymodelswerefounded.Inaccordance totheprincipleofthesameexceedingprobability,influencefactorsofspanforcharacteristic valuesofvehicleloadeffectswithvariousspanswereobtained,basedonwhich,therelationship betweenthepartialfactorsofvehicleloadeffectsandthespan ofbridge wasdetermined. Reliabilityanalysisforbridgedesign asperthedetermined vehicleload partialfactor-span relationshipwasmadewithFirst-orderSecond-momentmethod(FOSM).Theresultsshowthat thespaninfluencefactorandvehicleloadpartialfactorforcharacteristicvalueofvehicleload effect,which weredetermined based ontheequalexceeding probability,increase withthe decreaseofthespanofbridge.Theproposedspandependentpartialfactorcalculationformulafor vehicleloadforbridgedesignismorereasonable. DOI:10.19721/j.cnki.1001-7372.2015.06.009

60 中国公路学报 2015年 Key words:bridge engineering:load effect:probability model;partial factor;reliability 0引言 案模型、可靠度和分项系数进行了很多研究,但以桥 梁跨径为变量进行研究的不多,而桥梁跨径对桥梁 车辆荷载是公路桥梁设计的基本可变荷载 的可靠度影响较显著 般而言,中小跨径桥梁结构的恒荷载约占60%,车 本文中基于实测的车辆荷载数据,计算不同跨 辆荷载约占40%:大整径桥梁结构的恒荷载约占 径桥梁的车辆苟载效应,建立车辆荷载效应的截口 80%,车辆荷栽约占20%。中小骑径桥梁受车辆借 分布及设计基准期内最大值的概率分布,在相同保 证率的条件下,分析不同跨径桥梁车辆荷载效应 速发展,公路桥梁上的车辆荷载有增大的趋势 准值与规范车道荷载效应标准值的关系,提出不同 中小骑径桥梁被压垮的事件时有发生。高强材料的 跨径桥梁车辆荷载分项系数的计算公式,并给出了 使用致使桥梁结构日趋轻藏长细化,相比之下,车辆 建议值。最后,计算不同车辆荷载分项系数时桥梁 荷载占总荷载的比例逐渐增大,也会影响中小跨稻 桥梁的安全性。现行《公路桥涵设计通用规范 结构的可靠指标。 (JTG D60 2004)四中的车辆荷载分项系数是根 1 桥梁模型 不同跨径桥梁车辆荷载效应的综合概率模型,经过 本文以整体式简支和两跨连续钢筋混凝士T 可靠度分析确定的,不能反映桥梁跨径对可靠度的 形梁板桥为例进行分析,简支桥梁跨径为5 35 影响,实际上,大跨径桥梁和中小跨径桥粱对车辆花 两跨连续桥梁单跨跨径为2050m。桥梁单车道 载的敏感性不同。 因此,从可靠度水平 桥面板宽4,8m,主梁高度h一L/12,L为计算路 径。腹板厚度b=max{h/6,0.14}=max{L/72 合理。 0.14},主梁间距1.6m,横隔梁高度-3h/4-1 针对公路桥壑车辆荷载和可靠度间颗,中国众 16.翼缘悬出板厚0.08m,承托根部厚0.15m,横 多学者对其进行了大量研究。早在20世纪90年 隔梁宽0.12m:桥而铺装为0.05m厚沥青混凝士 代,中国曾在G207,G328.G305和G101四条国道 干线上各设置了 1个测点,对车辆荷载进行了调 面层(重度为21kN·m)和0.15m厚防水混凝 上垫层(重度为25kN·m),每侧栏杆及人行道 和实测),开展了桥梁可靠度研究,建立了桥梁车辆 重7kN·m1,截而计算简图如图1所示。 荷载效应的概率棹型,但该模型是不同跨径桥梁车 辆苟载效应的综合模型,不能反映不同跨径桥梁车 辆荷载效应的概率特征。最近,在西部交通科技项 日的支持下,通 新梦 习对中国23个省市69 路测站实测车辆荷载数据进行了收集和统计分析 发现车辆超载现象重。文献「7门、「81中根据公路 桥梁车镉荷载实测数据,分别建立了车辆荷载的截 图1湿凝士梁板桥计算截面 口概率分布和设计基准期内最大值的概率分布 Fig.I Caleulation Section of Concrete Beam-slab Bridge 献[9]中采用LRFD和AASHTO规定的荷载模 计算永久查我时,考虑跨内横路梁桥面铺装重 及LRFD抗力表达式,计算车辆荷载分项系数取不 量、人行道和栏杆的重量,等截面主梁的水久荷载为 同数值时桥梁结构的可靠指标,表明车辆荷载分项 均布荷载。假设桥梁施工过程中不发生结构体系转 系数取1.6或17时.不同跨径桥梁结构的可靠指 换,主梁自重作用于桥上时,结构已是最终体系。此 标基本趋于一致。文献[10]中基于动态称重荷载 时计算得到的随桥梁跨径变化的永久荷载标准值 测数据,分析了日平均交通量(ADTT)不同时的今 Rm(L)为 辆荷载分项系数。文献[11][13]中在实测车辆荷 0.5037/L+0.875L+C 载统计分析的基础上,分析了桥梁结构且有相同可 g(L)= Ls10 m (1) 靠度的情况下,车辆荷载分项系数的取值范围。综 -0.552/L-0.1224L+0.0863L2+ 合上述分析可以看出,尽管对公路桥梁车辆荷载 C 1>10m 1994-019 China Academic Joumal Electronic Publishing House.All rights reserved. http://www.cnki.ne
Keywords:bridgeengineering;loadeffect;probabilitymodel;partialfactor;reliability 0 引 言 车辆荷载是公路桥梁设计的基本可变荷载。一 般而言,中小 跨 径 桥 梁 结 构 的 恒 荷 载 约 占60%,车 辆荷载约 占 40%;大 跨 径 桥 梁 结 构 的 恒 荷 载 约 占 80%,车辆荷载约占20%。中小跨径桥梁受车辆荷 载的影响较大,调查表明,随着中国近年来经济的高 速发展,公路桥梁上的车辆荷载有增大的趋势[1-3], 中小跨径桥梁被压垮的事件时有发生。高强材料的 使用致使桥梁结构日趋轻薄长细化,相比之下,车辆 荷载占总荷载的比例逐渐增大,也会影响中小跨径 桥梁 的 安 全 性。现 行 《公 路 桥 涵 设 计 通 用 规 范》 (JTGD60—2004)[4]中的车辆荷载分项系数是根据 不同跨径桥梁车辆荷载效应的综合概率模型,经过 可靠度分析确定的,不能反映桥梁跨径对可靠度的 影响,实际上,大跨径桥梁和中小跨径桥梁对车辆荷 载的敏感性不同。因此,从可靠度水平一致的角度 考虑,采用考虑桥梁跨径的车辆荷载分项系数更为 合理。 针对公路桥梁车辆荷载和可靠度问题,中国众 多学 者 对 其 进 行 了 大 量 研 究。早 在20世 纪90年 代,中国曾在 G207,G328,G305和 G101四 条 国 道 干线上各设置了1个测点,对车辆荷载进行了调查 和实测[5],开展了桥梁可靠度研究,建立了桥梁车辆 荷载效应的概率模型,但该模型是不同跨径桥梁车 辆荷载效应的综合模型,不能反映不同跨径桥梁车 辆荷载效应的概率特征。最近,在西部交通科技项 目的支持下,逯一新等[6]对中国23个省市69个公 路测站实测车辆荷载数据进行了收集和统计分析, 发现车辆超载现象严重。文献[7]、[8]中根据公路 桥梁车辆荷载实测数据,分别建立了车辆荷载的截 口概率分布和设计基准期内最大值的概率分布。文 献[9]中采用 LRFD 和 AASHTO 规定的荷载模型 及 LRFD 抗力表达式,计算车辆荷载分项系数取不 同数值时桥梁结构的可靠指标,表明车辆荷载分项 系数取1.6或1.7时,不同跨径桥梁结构的可靠指 标基本趋于一致。文献[10]中基于动态称重荷载实 测数据,分析了日平均交通量(ADTT)不 同 时 的 车 辆荷载分项系数。文献[11]~[13]中在实测车辆荷 载统计分析的基础上,分析了桥梁结构具有相同可 靠度的情况下,车辆荷载分项系数的取值范围。综 合上述分析可以看出,尽管对公路桥梁车辆荷载概 率模型、可靠度和分项系数进行了很多研究,但以桥 梁跨径为变量进行研究的不多,而桥梁跨径对桥梁 的可靠度影响较显著。 本文中基于实测的车辆荷载数据,计算不同跨 径桥梁的车辆荷载效应,建立车辆荷载效应的截口 分布及设计基准期内最大值的概率分布,在相同保 证率的条件下,分析不同跨径桥梁车辆荷载效应标 准值与规范车道荷载效应标准值的关系,提出不同 跨径桥梁车辆荷载分项系数的计算公式,并给出了 建议值。最后,计算不同车辆荷载分项系数时桥梁 结构的可靠指标。 1 桥梁模型 本文以整 体 式 简 支 和 两 跨 连 续 钢 筋 混 凝 土 T 形梁板桥为例进行分析,简支桥梁跨径为5~35m, 两跨连续桥梁单跨跨径 为20~50m。桥 梁 单 车 道 桥面板宽 4.8 m,主 梁 高 度h=L/12,L 为 计 算 跨 径。腹 板 厚 度b=max{h/6,0.14}=max{L/72, 0.14},主梁间距1.6m,横隔梁高度h′ =3h/4 =L/ 16,翼缘悬出板厚0.08m,承 托 根 部 厚0.15m,横 隔梁宽0.12m;桥面铺装为0.05m 厚沥青混凝土 面层(重度为21kN·m-3)和0.15m 厚防水混凝 土垫层(重度 为25kN·m-3),每 侧 栏 杆 及 人 行 道 重7kN·m-1,截面计算简图如图1所示。 图1 混凝土梁板桥计算截面 Fig.1 CalculationSectionofConcreteBeam-slabBridge 计算永久荷载时,考虑跨内横隔梁、桥面铺装重 量、人行道和栏杆的重量,等截面主梁的永久荷载为 均布荷载。假设桥梁施工过程中不发生结构体系转 换,主梁自重作用于桥上时,结构已是最终体系。此 时计算得到的随桥梁跨径变化的永久荷载标准值 gDk(L)为 gDk(L)= -0.5037/L+0.875L+C1 L≤10m -0.552/L-0.1224L+0.0863L2+ C2 L> 烅 烄 烆 10m (1) 06 中 国 公 路 学 报 2015年
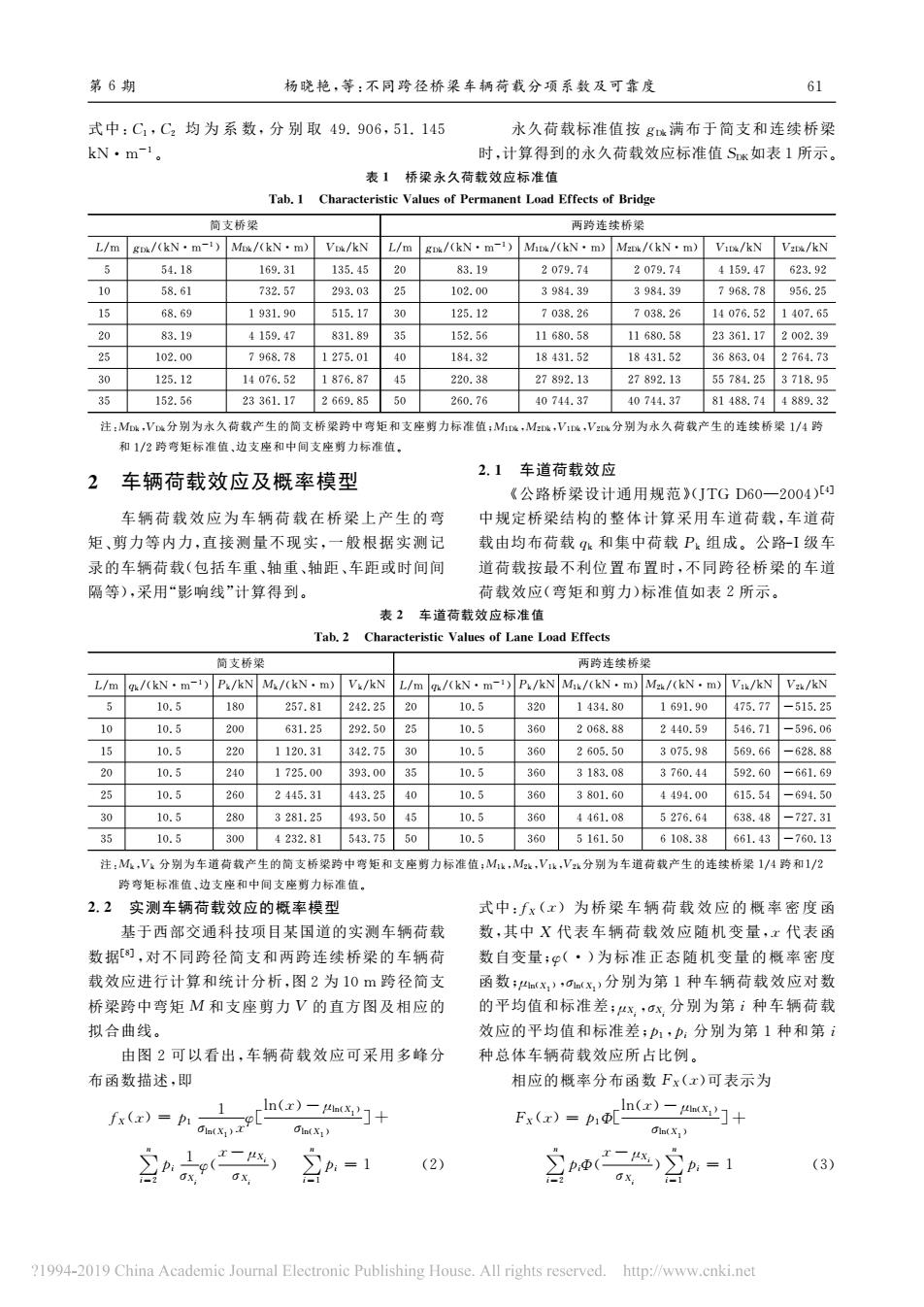
第6期 杨晓艳,等:不同跨径桥梁车柄荷载分项系数及可靠废 61 式中:C1,C均为系数,分别取49.906,51.145 永久荷载标准值按g满布于简支和连续桥梁 kN·m- 时,计算得到的水久荷载效应标准值Sx如表1所示。 表1桥梁永久荷载效应标准值 Tab.1 Characteristic Values of Permanent Load Effects of Bridge 简支桥染 调骑连续桥望 L/mEm/kN·m-')Mia/kN·mVm/kNL/mE/(kN·m-)Mm/(kN·mMa/kN·mVa/kNVa/kN 54.18 169.31 135.45 20 83.19 2079.74 2079.744150.47623.92 10 58.61 732.57 293.03 25 102.00 3984.39 3984.39 7968.78 956.25 15 68.69 1931.90 515.17 30 125.12 7038.26 7038.26 14076.52.1407.65 20 83.19 4159.47 831.89 35 152.56 11680.5811680.5823361.172002.39 25 102.00 7968.78 1275.01 40 184.32 18431.5218431.5236863.042764.73 30 125.12 14076.52 1876.87 45 220.38 27892.1327892.1355784.253718.95 35 152.56 23361.172669.8550 260.76 40744.3740744.3781488.744889.32 注,,V4分别为久荷产生的简支桥梁骑中矩和支座力标值:,,.分别为水久荷授产生的连使桥梁/A骑 和12验度标准边支和中支力标值 车辆荷载效应及概率模型 2.1车道荷载效应 《公路桥梁设计 通用规范(JTGD60 -2004) 车辆荷载效应为车辆荷栽在桥梁上产生的 中规定桥梁结构的整体计算采用车道荷载,车道荷 矩、剪力等内力,直接测量不现实,一般根据实测记 载由均布荷载和集中荷载P,组成。公路-I级车 录的车辆荷载(包括车重,轴重、轴距,车距或时间间 道荷载按最不利位置布置时,不同跨径桥梁的车道 隔等),采用“影响线”计算得到 荷载效应(弯矩和剪力)标准值如表2所示。 表2车道荷载效应标准值 Tah.2 Cha ristis Valuss of lane load Effests 商支桥 /mm/kN·m Pk/ Vi/k /mkN·m-/kNM/ 615.2 108 :M,分别为车道荷产生的简支桥梁骑中容矩和支座剪力标准值:M,M,V,Vk分别为车道荷载产生的连续桥梁1/4骑和1/2 、边座相 2.2 实测车辆荷载效应的概率模西 式中:fx(x)为桥梁车辆荷载效应的概率密度函 基于西部交通科技项目某国道的实测车辆荷载 数,其中X代表车辆荷载效应随机变量,x代表函 数据),对不同跨径简支和两跨连续桥梁的车辆荷 数自变量:心(·)为标准正态随机变量的概率密度 效应进行计算和统计分析,图2为10m踏径简支 分别为第1种车柄荷载效应对数 桥梁跨中弯矩M和支座剪力V的直方图及相应的 拟合曲线。 效应的平均值和标准差:力1,:分别为第1种和第 由图2可以看出,车辆荷载效应可采用多峰分种总体车辆荷载效应所占比例。 布函数描述,即 相应的概率分布函数Fx(x)可表示为 aAba]+ F,=h]+ (2) (3) . 1994-2019Chin Academic nal Electronic Publishing House.All rights http://www.cnki.ne
式中:C1,C2 均 为 系 数,分 别 取 49.906,51.145 kN·m-1。 永久荷载标准值按gDk满布于简支和连续桥梁 时,计算得到的永久荷载效应标准值SDK如表1所示。 表1 桥梁永久荷载效应标准值 Tab.1 CharacteristicValuesofPermanentLoadEffectsofBridge 简支桥梁 L/m gDk/(kN·m-1) MDk/(kN·m) VDk/kN 5 54.18 169.31 135.45 10 58.61 732.57 293.03 15 68.69 1931.90 515.17 20 83.19 4159.47 831.89 25 102.00 7968.78 1275.01 30 125.12 14076.52 1876.87 35 152.56 23361.17 2669.85 两跨连续桥梁 L/m gDk/(kN·m-1) M1Dk/(kN·m) M2Dk/(kN·m) V1Dk/kN V2Dk/kN 20 83.19 2079.74 2079.74 4159.47 623.92 25 102.00 3984.39 3984.39 7968.78 956.25 30 125.12 7038.26 7038.26 14076.52 1407.65 35 152.56 11680.58 11680.58 23361.17 2002.39 40 184.32 18431.52 18431.52 36863.04 2764.73 45 220.38 27892.13 27892.13 55784.25 3718.95 50 260.76 40744.37 40744.37 81488.74 4889.32 注:MDk,VDk分别为永久荷载产生的简支桥梁跨中弯矩和支座剪力标准值;M1Dk,M2Dk,V1Dk,V2Dk分别为永久荷载产生的连续桥梁1/4跨 和1/2跨弯矩标准值、边支座和中间支座剪力标准值。 2 车辆荷载效应及概率模型 车 辆 荷 载 效 应 为 车 辆 荷 载 在 桥 梁 上 产 生 的 弯 矩、剪力等内力,直接测量不现实,一般根据实测记 录的车辆荷载(包括车重、轴重、轴距、车距或时间间 隔等),采用“影响线”计算得到。 2.1 车道荷载效应 《公路桥梁设计通用规范》(JTGD60—2004)[4] 中规定桥梁结构的整体计算采用车道荷载,车道荷 载由均布荷载qk 和集中荷载Pk 组成。公路-I级车 道荷载按最不利位置布置时,不同跨径桥梁的车道 荷载效应(弯矩和剪力)标准值如表2所示。 表2 车道荷载效应标准值 Tab.2 CharacteristicValuesofLaneLoadEffects 简支桥梁 L/m qk/(kN·m-1)Pk/kN Mk/(kN·m) Vk/kN 5 10.5 180 257.81 242.25 10 10.5 200 631.25 292.50 15 10.5 220 1120.31 342.75 20 10.5 240 1725.00 393.00 25 10.5 260 2445.31 443.25 30 10.5 280 3281.25 493.50 35 10.5 300 4232.81 543.75 两跨连续桥梁 L/m qk/(kN·m-1)Pk/kN M1k/(kN·m)M2k/(kN·m)V1k/kN V2k/kN 20 10.5 320 1434.80 1691.90 475.77 -515.25 25 10.5 360 2068.88 2440.59 546.71 -596.06 30 10.5 360 2605.50 3075.98 569.66 -628.88 35 10.5 360 3183.08 3760.44 592.60 -661.69 40 10.5 360 3801.60 4494.00 615.54 -694.50 45 10.5 360 4461.08 5276.64 638.48 -727.31 50 10.5 360 5161.50 6108.38 661.43 -760.13 注:Mk,Vk 分别为车道荷载产生的简支桥梁跨中弯矩和支座剪力标准值;M1k,M2k,V1k,V2k分别为车道荷载产生的连续桥梁1/4跨和1/2 跨弯矩标准值、边支座和中间支座剪力标准值。 2.2 实测车辆荷载效应的概率模型 基于西部交通科技项目某国道的实测车辆荷载 数据[8],对不同跨径简支和两跨连续桥梁的车辆荷 载效应进行计算和统计分析,图2为10m 跨径简支 桥梁跨中弯矩 M 和支座剪力V 的直方图及相应的 拟合曲线。 由图2可以看出,车辆荷载效应可采用多峰分 布函数描述,即 fX(x)=p1 1 σln(X1)xφ[ ln(x)-μln(X1) σln(X1) ]+ ∑ n i=2 pi 1 σXi φ( x-μXi σXi ) ∑ n i=1 pi =1 (2) 式中:fX (x)为桥梁车辆荷载效应的概率密度函 数,其中 X 代 表 车 辆 荷 载 效 应 随 机 变 量,x 代 表 函 数自变量;φ(·)为标准正态随机变量的概率密度 函数;μln(X1),σln(X1)分别为第1种车辆荷载效应对数 的平均值和标准差;μXi,σXi分 别 为 第i 种 车 辆 荷 载 效应的平均值和标准差;p1,pi 分别为第1种和第i 种总体车辆荷载效应所占比例。 相应的概率分布函数FX(x)可表示为 FX(x)=p1Φ[ ln(x)-μln(X1) σln(X1) ]+ ∑ n i=2 piΦ( x-μXi σXi )∑ n i=1 pi =1 (3) 第6期 杨晓艳,等:不同跨径桥梁车辆荷载分项系数及可靠度 16
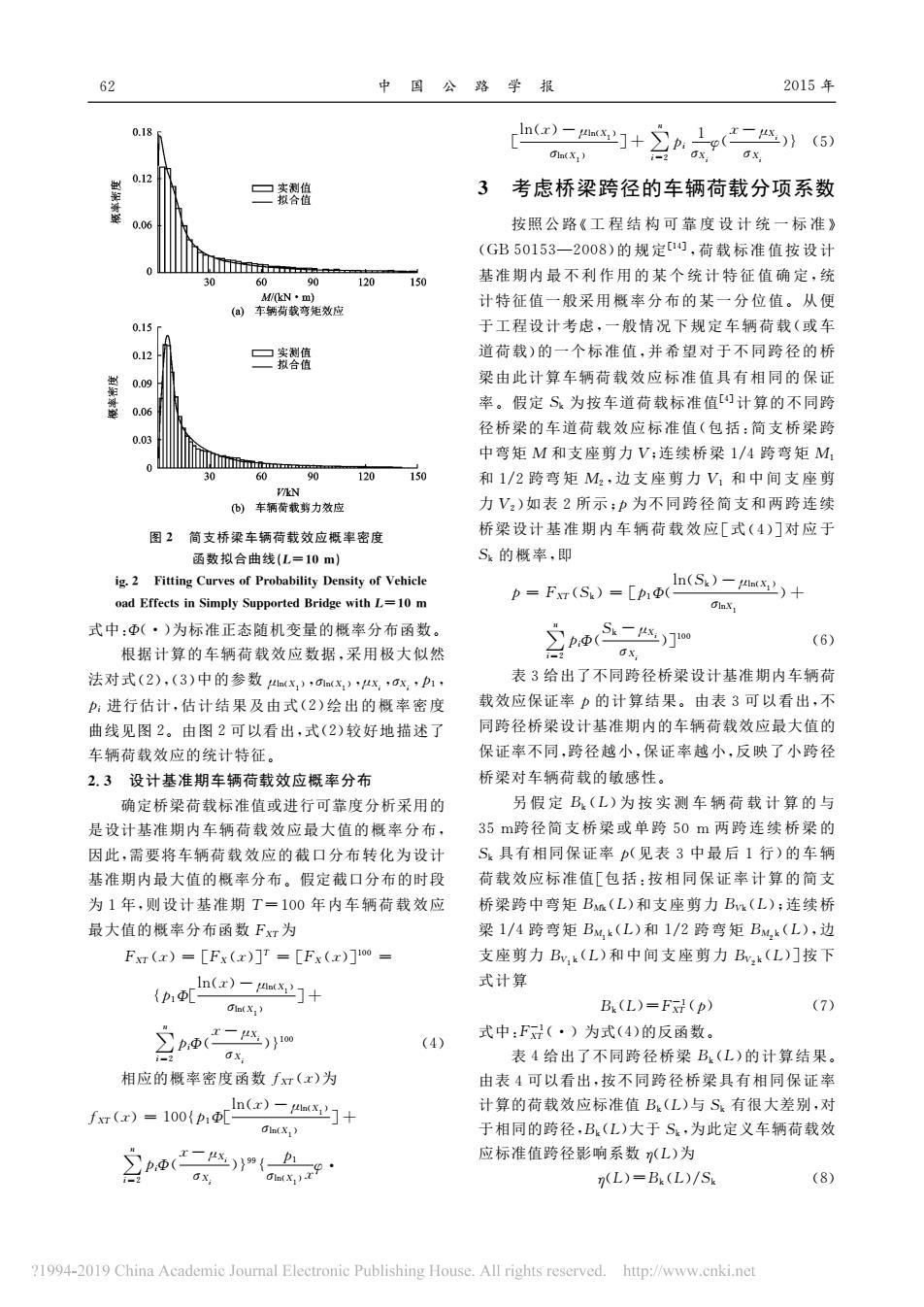
6品 中国公路学报 2015年 bo]+名女》 0.12 已责件 3考虑桥梁跨径的车辆荷载分项系数 按照公路《工程结构可靠度设计统一标准》 (GB50153一2008)的规定),荷载标准值按设计 120 150 基准期内最不利作用的某个统计特征值确定,统 计特征值一般采用概率分布的某一分位值。从便 .15 于工程设计考虑,一般情况下规定车辆荷载(或车 0.12 二教信 道荷载)的一 个标准值,并希望对于不同跨径的 梁由此计算车辆荷载效应标准值具有相同的保证 0.05 率。假定S为按车道荷找标准信[幻计算的不司黔 径桥梁的车道荷载效应标准值(包括:简支桥梁 0.03 中弯矩M和支座剪力V:连续桥梁1/4跨弯矩M 90120 150 和1/2跨弯矩M,边支座剪力V1和中间支座剪 力V:)如表2所示:p为不同跨径简支和两跨连续 困?简支桥梁车辆荷载效应概率密度 桥梁设计基准期内车辆荷载效应[式(4)门对应于 西数拟合曲线L一10m) S的概率,即 式中:(·)为标准正态随机变量的概率分布函数 根据计算的车辆荷载效应数据,采用极大似然 (6) GX. 法对式(2),(3)中的参数 表3给出了不同跨径桥梁设计基准期内车辆荷 载效应保证率力的计算结果。由表3可以看出,不 曲线见图2。由图2可以看出,式(2)较好地描述了 同跨径桥梁设计基准期内的车辆荷栽效应最大值的 车辆荷载效应的统计特征。 保证率不同,跨径越小,保证率越小,反映了小跨径 2.3设计基准期车辆荷载效应概率分布 桥梁对车辆荷载的敏感性。 确定桥梁荷载标准值或进行可靠度分析采用的 另假定B(L)为按实测车辆荷载计算的与 是设计基准期内车辆荷载效应最大值的概率分布 35m跨径简支桥架或单跨50m两跨连续桥梁的 因此,需要将车辆荷载效应的截口分布转化为设计 S.其有相同保证率D(见表3中最后1行)的车辆 基准期内最大值的概率分布、假定哉口分布的时段 荷载效应标准值「包括,按相同保证率计算的简支 为1年,则设计基准期T 100年内车辆荷载效应 桥梁跨中弯矩Ba(L)和支座剪力B(L):连续桥 最大值的概率分布函数Fx,为 梁1/4跨弯矩B,k(L)和1/2跨弯矩B(L),边 F(x)=「Fx(x)1t=「Fx(x)Tom= 支座剪力B,(L)和中间支座剪力B,(L)]按下 ,)二]十 式计算 B(L)=F(p》 (7) (4) 式中:F(·)为式(4)的反函数。 表4给出了不同跨径桥梁B(L)的计算结果 相应的概率密度函数f知(x)为 由表4可以看出,按不同跨径桥梁具有相同保证率 fr=1]+ 计算的荷载效应标准值队L)与有很大差别, dhx) 于相同的跨径,B,(L)大于S,为此定义车辆荷载效 应标准值跨径影响系数L)为 7(L)=B(L)/S (8) 1994-2019 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.enki.ne
图2 简支桥梁车辆荷载效应概率密度 函数拟合曲线(L=10m) F ig.2 FittingCurvesofProbabilityDensityofVehicle L oadEffectsinSimplySupportedBridgewithL=10m 式中:Φ(·)为标准正态随机变量的概率分布函数。 根据计算的车辆荷载效应数据,采用极大似然 法对式(2),(3)中的参数μln(X1),σln(X1),μXi,σXi,p1, pi 进行估计,估 计 结 果 及 由 式(2)绘出的概率密度 曲线见图2。由图2可以看出,式(2)较好地描述了 车辆荷载效应的统计特征。 2.3 设计基准期车辆荷载效应概率分布 确定桥梁荷载标准值或进行可靠度分析采用的 是设计基准期内车辆荷载效应最大值的概率分布, 因此,需要将车辆荷载效应的截口分布转化为设计 基准期内最大值的概率分布。假定截口分布的时段 为1年,则设计基准期 T=100年 内 车 辆 荷 载 效 应 最大值的概率分布函数FXT为 FXT (x)= [FX(x)]T = [FX(x)]100 = {p1Φ[ ln(x)-μln(X1) σln(X1) ]+ ∑ n i=2 piΦ( x-μXi σXi )}100 (4) 相应的概率密度函数fXT (x)为 fXT (x)=100{p1Φ[ ln(x)-μln(X1) σln(X1) ]+ ∑ n i=2 piΦ( x-μXi σXi )}99{ p1 σln(X1)xφ· [ ln(x)-μln(X1) σln(X1) ]+ ∑ n i=2 pi 1 σXi φ( x-μXi σXi )} (5) 3 考虑桥梁跨径的车辆荷载分项系数 按照公 路 《工程结构可靠度设计统一标准》 (GB50153—2008)的 规 定[14],荷 载 标 准 值 按 设 计 基准期内最不利作用的某个统计特 征值确定,统 计特征值一般采用概率分布的某一分位值。从 便 于工程设计考虑,一般情况下规定车辆荷载(或 车 道荷载)的一个标 准 值,并希望对于不同跨径的桥 梁由此计算车辆荷 载 效 应 标 准 值 具 有 相 同 的 保 证 率。假定Sk 为按车道荷载标准值[4]计算的不同跨 径桥梁的车道荷载效应标准值(包 括:简 支 桥 梁 跨 中弯矩 M 和支座剪力V;连续 桥 梁1/4跨 弯 矩 M1 和1/2跨弯 矩 M2,边 支 座 剪 力V1 和 中 间 支 座 剪 力V2)如表2所示;p为不同跨径简支和两跨连续 桥梁设计基准期内车辆荷载效应[式(4)]对 应 于 Sk 的概率,即 p =FXT (Sk)= [p1Φ( ln(Sk)-μln(X1) σlnX1 )+ ∑ n i=2 piΦ( Sk -μXi σXi )]100 (6) 表3给出了不同跨径桥梁设计基准期内车辆荷 载效应保证率p 的计算结果。由表3可以看出,不 同跨径桥梁设计基准期内的车辆荷载效应最大值的 保证率不同,跨径越小,保证率越小,反映了小跨径 桥梁对车辆荷载的敏感性。 另 假 定 Bk(L)为 按 实 测 车 辆 荷 载 计 算 的 与 35m跨径简 支 桥 梁 或 单 跨50 m 两 跨 连 续 桥 梁 的 Sk 具有相同保证率p(见 表3中 最 后1行)的 车 辆 荷载效应标准值[包 括:按相同保证率计算的简支 桥梁跨中弯矩BMk(L)和支座 剪 力 BVk(L);连 续 桥 梁1/4跨弯矩 BM1k(L)和1/2跨 弯 矩 BM2k(L),边 支座剪力 BV1k(L)和 中 间 支 座 剪 力 BV2k(L)]按 下 式计算 Bk(L)=F-1 XT (p) (7) 式中:F-1 XT (·)为式(4)的反函数。 表4给出了不同跨径桥梁 Bk(L)的计算结果。 由表4可以看出,按不同跨径桥梁具有相同保证率 计算的荷载效应标准值Bk(L)与Sk 有很大差别,对 于相同的跨径,Bk(L)大于Sk,为此定义车辆荷载效 应标准值跨径影响系数η(L)为 η(L)=Bk(L)/Sk (8) 26 中 国 公 路 学 报 2015年
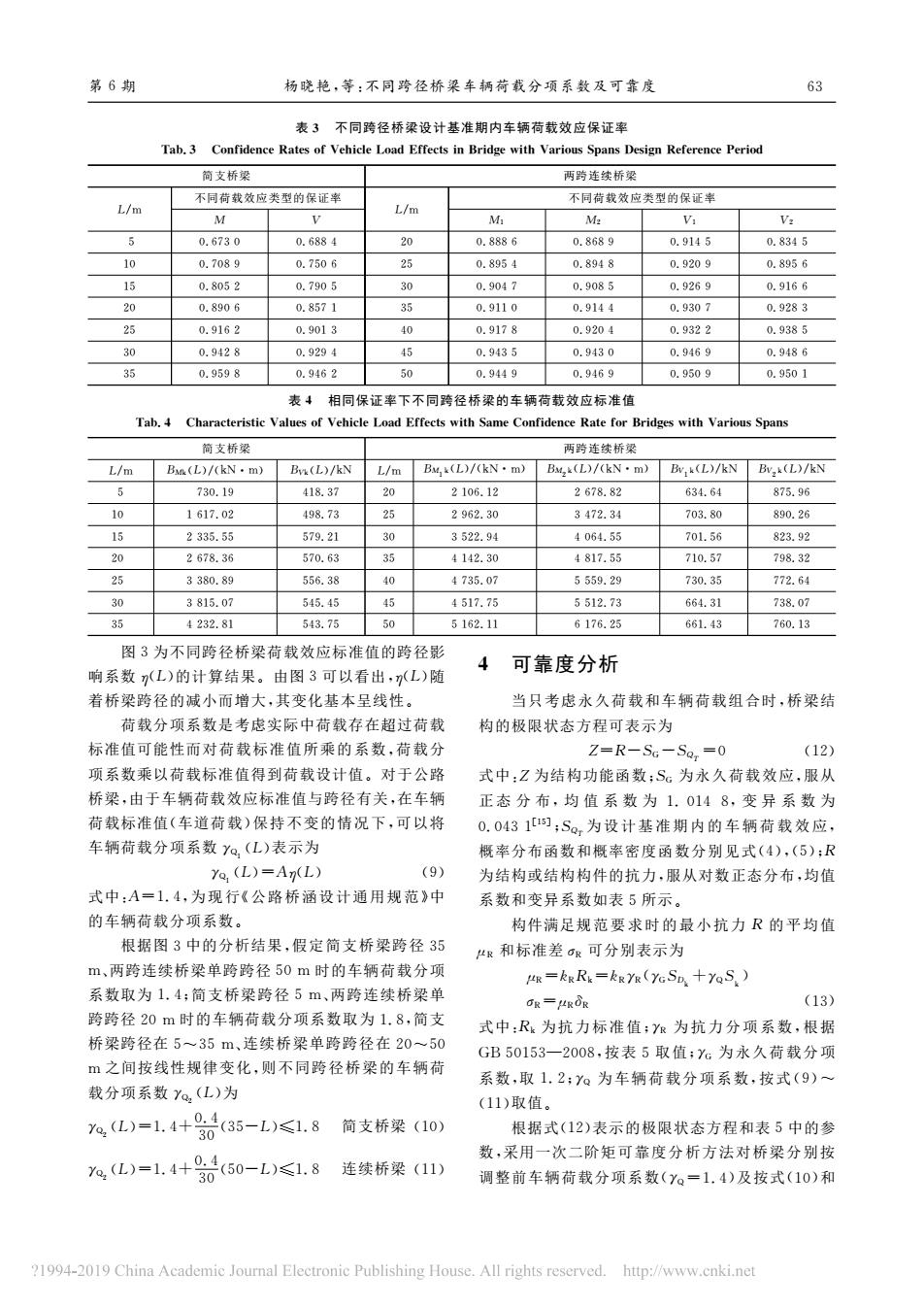
第6期 杨晓艳,等:不同跨径桥梁车柄荷载分项系数及可靠 63 表3不同跨径桥梁设计基准棚内车辆荷载效应保证 Tab.3 Confidence Rat 简支桥 两骑连线桥架 不问荷载效应类型的保证率 不问荷载效应类型的保证等 L/m L/m 0.6884 20 0.888 0.8689 0.914 0.834号 0,708 0.7509 2 0.895 0.8948 09209 0.895 0805 0.904 0.908 0926 0.6 0.85 0.91 928 0.916 0.901 0.91 0.943 0.943 0946 0.9149 0.9469 0.9509 表4相同保证率下不同跨径桥梁的车辆荷载效应标准值 Tab,4 Characteristic Values of Vehicle Load Effects with Same Confidence Rate for Bridges with Various Spans 简支桥 两跨连线桥 B()kN mB(kN mBy MLCkN.m)B K(L/CN m)BMLMkN By ML)/kN 730.19 11及37 2106.12 267882 64 875.06 161709 5 9g6230 347934 800.26 93555 57021 352994 1a6A55 0156 82302 267836 5TD.63 35 4142.30 4817.55 710.57 798.32 3380.89 55638 0 4735.07 5559.29 730.35 男7264 30 3R15.07 545.45 45 451795 551273 664.31 93807 35 4232.81 543.75 50 5182.11 6176.25 66L.43 760.13 图3为不同跨径桥梁荷载效应标准值的跨径影 4 可靠度分析 响系数(L)的计算结果。由图3可以看出,L)随 着桥梁跨径的减小而增大,其变化基本呈线性】 当只考虑水久荷载和车辆荷载组合时,桥梁结 荷载分项系数是老虑实际中荷载存在超过荷载 构的极限状态方程可表示为 标准值可能性而对荷我标准值所乘的系数,荷载 =R-S-S,=0 (12 项系数乘以荷载标准值得到荷载设计值。对于公路 式中:Z为结构功能函数:S,为永久荷载效应,服从 桥梁,由于车辆荷载效应标准值与跨径有关,在车钙 正态分布,均值系数为1.0148,变异系数为 荷载标准值(车道荷载)保持不变的情况下,可以将 0.0431S,为设计基准期内的车辆荷载效应, 车辆荷载分项系数,(L)表示为 概率分布函数和概率密度函数分别见式(4),(5): yo (L)-Ax(L 9 为结构或结构构件的抗力,服从对数正态分布,均值 式中:A=1.4,为现行《公路桥通设计通用规范》中 系数和变异系数如表5所示。 的车辆荷载分项系数。 物件满足规范要求时的最小抗力R的平均俏 根据图3中的分析结果,假定简支桥梁跨径35 和标准差R可分别表示为 m,两跨连续桥梁单跨跨径50m时的车辆荷载分项 g=kgR=kgyn(cSn+yoS】 系数取为1.4:简支桥梁跨径5,两跨连续桥梁 (13 跨跨径20m时的车辆荷载分项系数取为1.8,简支 式中:R为抗力标准值:为抗力分项系数,根据 桥梁跨径在5一35m,连续桥梁单跨跨径在20-~50 GB50153一2008,按表5取值:Y:为永久荷载分项 m之间按线性规律变化,则不同跨径桥梁的车辆荷 系数,取1.2:y。为车辆荷载分项系数,按式(9)一 载分项系数Y,(L)为 (11)取值 y%(L)=1.4+04(35-L)≤1.8简支桥梁(10) 根据式(12)表示的极限状态方程和表5中的参 数,采用一次二阶矩可靠度分析方法对桥梁分别按 %(L)=1.4+00(50-L)≤1.8连续桥梁(11) 调整前车辆荷载分项系数(Y。=1.4)及按式(10)和 1994-2019Chin Academic Jou mal Electronic Publishing House.All rights reserved http://www.cnki.ne
表3 不同跨径桥梁设计基准期内车辆荷载效应保证率 Tab.3 ConfidenceRatesofVehicleLoadEffectsinBridgewithVariousSpansDesignReferencePeriod 简支桥梁 L/m 5 10 15 20 25 30 35 不同荷载效应类型的保证率 M V 0.6730 0.6884 0.7089 0.7506 0.8052 0.7905 0.8906 0.8571 0.9162 0.9013 0.9428 0.9294 0.9598 0.9462 两跨连续桥梁 L/m 20 25 30 35 40 45 50 不同荷载效应类型的保证率 M1 M2 V1 V2 0.8886 0.8689 0.9145 0.8345 0.8954 0.8948 0.9209 0.8956 0.9047 0.9085 0.9269 0.9166 0.9110 0.9144 0.9307 0.9283 0.9178 0.9204 0.9322 0.9385 0.9435 0.9430 0.9469 0.9486 0.9449 0.9469 0.9509 0.9501 表4 相同保证率下不同跨径桥梁的车辆荷载效应标准值 Tab.4 CharacteristicValuesofVehicleLoadEffectswithSameConfidenceRateforBridgeswithVariousSpans 简支桥梁 L/m BMk(L)/(kN·m) BVk(L)/kN 5 730.19 418.37 10 1617.02 498.73 15 2335.55 579.21 20 2678.36 570.63 25 3380.89 556.38 30 3815.07 545.45 35 4232.81 543.75 两跨连续桥梁 L/m BM1k(L)/(kN·m) BM2k(L)/(kN·m) BV1k(L)/kN BV2k(L)/kN 20 2106.12 2678.82 634.64 875.96 25 2962.30 3472.34 703.80 890.26 30 3522.94 4064.55 701.56 823.92 35 4142.30 4817.55 710.57 798.32 40 4735.07 5559.29 730.35 772.64 45 4517.75 5512.73 664.31 738.07 50 5162.11 6176.25 661.43 760.13 图3为不同跨径桥梁荷载效应标准值的跨径影 响系数η(L)的计算结果。由图3可以看出,η(L)随 着桥梁跨径的减小而增大,其变化基本呈线性。 荷载分项系数是考虑实际中荷载存在超过荷载 标准值可能性而对荷载标准值所乘的系数,荷载分 项系数乘以荷载标准值得到荷载设计值。对于公路 桥梁,由于车辆荷载效应标准值与跨径有关,在车辆 荷载标准值(车道荷载)保持不变的情况下,可以将 车辆荷载分项系数γQ1 (L)表示为 γQ1 (L)=Aη(L) (9) 式中:A=1.4,为 现 行《公 路 桥 涵 设 计 通 用 规 范》中 的车辆荷载分项系数。 根据图3中的分析结果,假定简支桥梁跨径35 m、两跨连续桥梁单跨跨径50m 时的车辆荷载分项 系数取为1.4;简支桥梁跨径5m、两跨连续桥梁单 跨跨径20m 时的车辆荷载分项系数取为1.8,简支 桥梁跨径在5~35m、连续桥梁单跨跨径在20~50 m 之间按线性规律变化,则不同跨径桥梁的车辆荷 载分项系数γQ2 (L)为 γQ2 (L)=1.4+0.4 30(35-L)≤1.8 简支桥梁 (10) γQ2 (L)=1.4+0.4 30(50-L)≤1.8 连续桥梁 (11) 4 可靠度分析 当只考虑永久荷载和车辆荷载组合时,桥梁结 构的极限状态方程可表示为 Z=R-SG-SQT =0 (12) 式中:Z 为结构功能函数;SG 为永久荷载效应,服从 正 态 分 布,均 值 系 数 为 1.014 8,变 异 系 数 为 0.0431[15];SQT为 设 计 基 准 期 内 的 车 辆 荷 载 效 应, 概率分布函数和概率密度函数分别见式(4),(5);R 为结构或结构构件的抗力,服从对数正态分布,均值 系数和变异系数如表5所示。 构件满足规 范 要 求 时 的 最 小 抗 力 R 的 平 均 值 μR 和标准差σR 可分别表示为 μR=kRRk=kRγR(γGSDk +γQSk ) σR=μRδR (13) 式中:Rk 为抗 力 标 准 值;γR 为 抗 力 分 项 系 数,根 据 GB50153—2008,按表5取值;γG 为永久 荷 载 分 项 系数,取1.2;γQ 为 车 辆 荷 载 分 项 系 数,按 式(9)~ (11)取值。 根据式(12)表示的极限状态方程和表5中的参 数,采用一次二阶矩可靠度分析方法对桥梁分别按 调整前车辆荷载分项系数(γQ =1.4)及按式(10)和 第6期 杨晓艳,等:不同跨径桥梁车辆荷载分项系数及可靠度 36

中国公路学报 2015年 表5统一标准中的抗力分项系 2 已 Tab.5 ee in o. 构件受力 统计黎冠 均值系数变系数抗力分项 分布类 L6月 状态 系数钢 2 受 1.22620.14141.1254 对数正态 曼写(T形)2.17980.22301.2521 分 08 10 15 25 30 35 算结果平均值分别如表6,7所示。 由表6,7可以看出,当简支桥梁按式(10)、连续 日 桥梁按式(11)确定车辆荷载分项系数时,可靠指标 虽有提高,但仍不能达到简支桥梁跨径35m、连续 桥梁单跨跨径50m时的可靠指标。这是因为虽然 日 分项系数表达式(10)和(11)是按相同保证率确启 的,但保证不是很高(约0.95):而如图4所示,设 计基准期内车辆荷载效应的变异系数L)随跨径 2530 40 45 的变化很大,按式(10)和(11)调整的车辆分项系数 心两跨连续桥果弯炮 不能弥补因变异系数随跨径减小而增大所降低的可 靠指标。如果简支桥梁踏径35m、两跨连续桥梁单 16 日辛变 跨跨径50m时的车辆荷载分项系数取为1.4,简支 桥梁跨径5m、两跨连续桥梁单跨跨径20m时的车 12 辆荷载分项系数分别取为2.0,2.5,3.0,简支桥梁 骑径在5一35m.连续桥梁单骑骑径在20一50m之 间按线性想律变化,计算的可常指标也列于表6 2530 35 40 45 50 由表6可以看出 当简支桥梁跨径5m,两跨连续桥 梁单跨跨径20时的车辆荷载分项系数取为3 困3车辆荷载效应标准值跨径影响系数随跨径的变化 时,不同跨径桥梁的可靠指标才基本上达到简支桥 Fig. 垫路径35m、车续桥经单跨跨径50m时的可靠指 标,但工程设计中取这样的分项系数不现实,仍球议 (1)示的分项系数进行可度分析,可靠指标 按式(10)和(11)取用 举 不同径筒支桥梁结构的可靠指标 Tab.6 Reliability Indices for Various s of Simply Supported Bridge 受弯状态 受明状态 不同跨径L(m)下的可靠标值 不同跨径上(m)下的可靠指标值 极 51015 20 25 3035 5101520253035 L.12.7562.8772.953.1153.1633.3893.630.9073723.85339714.0904.08326340.912 8调网。7 3.6630.60939634.0144.0754.1534.194.3464.6340.671 4.1704.3714.6340.567 2.53.453.4533563.4573.4373.4963.6630218.292306.3144.32 4.2281.394.6310.342 3.03.6623.6333.6013.5693.5453.5343.6630.0014.479.4564.4294.4164.278.4234.630.155 注:为为简支桥梁跨径5m时的车辆荷载分项系数:极差指该组数豁中最大值与最小值的差值,下问, 5结语 分布,报率密度函数可用】个对数正奏密度函数和 1一3个正态密度函数的加权和表示 (1)采用中国近年来实测的车辆荷载数据,对实 (2)基于实测车辆荷载确定的相同分位值的车 测车辆荷载在桥梁结构上所产生的车辆荷载效应进 辆荷载效应标准值随桥梁跨径的减小而增大。 行概率分析,得到车辆荷效应的截口分布呈多蜂 (3)采用提出的根据桥梁跨径按线性规律调整 1994-2019 China Academic Joumal Electronic Publishing House.All rights reserved. http://www.cnki.ne
图3 车辆荷载效应标准值跨径影响系数随跨径的变化 Fig.3 InfluenceFactorsofSpanforCharacteristic ValueofVehicleLoadvs.SpanofBridge (11)表示的分项系数进行可靠度分析,可靠指标计 表5 统一标准中的抗力分项系数 Tab.5 PartialFactorsofResistanceinUnifiedStandard 构件受力 状态 受弯 受剪(T形) 统计参数 均值系数 kR 变异系数 δR 抗力分项 系数γR 1.2262 0.1414 1.1254 2.1798 0.2230 1.2521 分布类型 对数正态 分布 算结果平均值分别如表6,7所示。 由表6,7可以看出,当简支桥梁按式(10)、连续 桥梁按式(11)确定车辆荷载分项系数时,可靠指标 虽有提高,但仍不能达到简支桥梁跨径35m、连 续 桥梁单跨跨径50m 时的可靠指标。这是因为虽然 分项系数表 达 式(10)和(11)是按相同保证率确定 的,但保证率不是很高(约0.95);而如图4所示,设 计基准期内车辆荷载效应的变异系数δ(L)随 跨 径 的变化很大,按式(10)和(11)调整的车辆分项系数 不能弥补因变异系数随跨径减小而增大所降低的可 靠指标。如果简支桥梁跨径35m、两跨连续桥梁单 跨跨径50m 时的车辆荷载分项系数取为1.4,简支 桥梁跨径5m、两跨连续桥梁单跨跨径20m 时的车 辆荷载分项系数分别取为2.0,2.5,3.0,简支桥 梁 跨径在5~35m、连续桥梁单跨跨径在20~50m 之 间按 线 性 规 律 变 化,计 算 的 可 靠 指 标 也 列 于 表 6。 由表6可以看出:当简支桥梁跨径5m、两跨连续桥 梁单跨跨径20m 时的车辆荷载分项系数取为3.0 时,不同跨径桥梁的可靠指标才基本上达到简支桥 梁跨径35m、连续桥梁单跨跨径50m 时的可靠指 标,但工程设计中取这样的分项系数不现实,仍建议 按式(10)和(11)取用。 表6 不同跨径简支桥梁结构的可靠指标 Tab.6 ReliabilityIndicesforVariousSpansofSimplySupportedBridges γ1 受弯状态 不同跨径L(m)下的可靠指标值 5 10 15 20 25 30 35 极差 受剪状态 不同跨径L(m)下的可靠指标值 5 10 15 20 25 30 35 极差 1.4 2.756 2.877 2.995 3.115 3.163 3.389 3.663 0.907 3.722 3.853 3.971 4.090 4.088 4.332 4.634 0.912 1.8 3.054 3.124 3.189 3.256 3.315 3.430 3.663 0.609 3.963 4.014 4.075 4.153 4.119 4.346 4.634 0.671 2.0 3.179 3.230 3.276 3.321 3.383 3.451 3.663 0.484 4.067 4.126 4.176 4.233 4.170 4.371 4.634 0.567 2.5 3.445 3.453 3.456 3.457 3.437 3.496 3.663 0.218 4.292 4.306 4.314 4.332 4.228 4.399 4.634 0.342 3.0 3.662 3.633 3.601 3.569 3.545 3.534 3.663 0.001 4.479 4.456 4.429 4.416 4.278 4.423 4.634 0.155 注:γ1 为简支桥梁跨径5m 时的车辆荷载分项系数;极差指该组数据中最大值与最小值的差值,下同。 5 结 语 (1)采用中国近年来实测的车辆荷载数据,对实 测车辆荷载在桥梁结构上所产生的车辆荷载效应进 行概率分析,得到车辆荷载效应的截口分布呈多峰 分布,概率密度函数可用1个对数正态密度函数和 1~3个正态密度函数的加权和表示。 (2)基于实测车辆荷载确定的相同分位值的车 辆荷载效应标准值随桥梁跨径的减小而增大。 (3)采用提出的根据桥梁跨径按线性规律调整 46 中 国 公 路 学 报 2015年

第6期 杨晓艳,等:不同跨径桥梁车柄荷载分项系数及可靠 65 表】不同径连键桥梁结构的可克指标 Tab.7 Reliability Indices for Var Spans of Contingous Twe-eaual span Bridge 受弯状老 受期状态 不问跨径上(m)下的可靠指标 极差 极差 20 20 30 4550 1.42.70 3.2 88.1404.2910.773 1.82,89 D,478 4.081.1594.2910,624 2,98 3.6503,7623,92 0514.1 3.03.3143.20 3.2413.3183.3493.3623.37 0.0614.004 3.8673.9354.0514.1364.2114.2910.28 注:作为连续桥量单奇骑径20m时的车辆荷载分项系数: 值进行了研究,并未考虑永久荷载效应和抗力统计 0.85 参数的发展变化。建议在全国范围内开展永久荷载 和抗力统计参数的调研,研究各效应分项系数的取 058 值,这对现行规范的修订将更具有参考意义。 日装出等别 参考文献: References 031 15 25 30 w级装 [1门贡金,李文杰,赵有黎,等.公路桥梁车辆荷概率 型研究《一) 一非治超地区[U门.公路交通科技 085 2010.27(6),4045.57 0.78 令膀客图 GONG Jin-xin,LI Wer-jie,ZHAO Jun-li.et al.Re 064 hicle oads (1)-Nor ea[J] ion R 057 search and Develop 010,276):40-45.5 2530354045 [2] 公路桥梁车辆荷载概率 侧有时绿标专相 摸型研究 收费地区和强制治超地网 00 小.公路交通科技 2010.27(7):56-60 0.77 文变塑由, GONG Jin-xi in.LI Wen-jie,ZHAO Jun-li.et al.Re rch n Probabilist Model of Highway Bridge Ve hicle Loads()-Toll-by-weight Area and Overload 051 Controlling Area[]].Journal of Highway and Trans 038 portation Research and Development.2010.27(7):56 60 2530 50 3 LIU Xiao-gang.FAN Jian-sheng.NIE Jian-guo.et al Behavior of Composite Rigid Frame Bridge Under Bi directional Seismic Excitations[].Journal of Traffic 图·设计基准期内车柄荷载效应变异系数 and Transportation Engineering:English Edition 随跨径的变化(T=10年) 2014.1(1):62-71. icient of Vehicle Load Effect in Desion Reference period ys Span of Bridee [4]JTGD60一2004,公路桥涵设计通用规范[S]. 的车辆背费分项系数计算的桥设结构可常指标,出 JTG D60-2004.General Code for Design of Highway Bridges and Culverts[S]. 按现行规范中规定的车辆荷载分项系数取1.4计算 [5]贡金鑫,杨晓艳,贺拴海,等.荷载组合方法与系数的 的桥梁结构可靠指标更合理。 研究[R].北京:中交公路规划设计院有限公司 (4)本文是在固定水久荷载效应分项系数的前 2011. 提下,对中、小跨径桥梁结构车辆荷载分项系数的取 GONG Jirxin.YANG Xiao-yan.HE Shuarr-hai.et al. 1994-019 China Academic Joumal Electronic Publishing House rights erved. http://www.cnki.net
表7 不同跨径连续桥梁结构的可靠指标 Tab.7 ReliabilityIndicesforVariousSpansofContinuousTwo-equalSpanBridges γ2 受弯状态 不同跨径L(m)下的可靠指标值 20 25 30 35 40 45 50 极差 受剪状态 不同跨径L(m)下的可靠指标值 20 25 30 35 40 45 50 极差 1.4 2.701 2.696 2.815 2.987 3.120 3.244 3.375 0.673 3.517 3.477 3.625 3.823 3.988 4.140 4.291 0.773 1.8 2.897 2.859 2.949 3.089 3.188 3.278 3.375 0.478 3.667 3.596 3.718 3.890 4.031 4.159 4.291 0.624 2.0 2.981 2.930 3.009 3.136 3.220 3.294 3.375 0.394 3.733 3.650 3.762 3.922 4.051 4.169 4.291 0.558 2.5 3.163 3.081 3.137 3.235 3.290 3.331 3.375 0.212 3.879 3.768 3.856 3.992 4.097 4.192 4.291 0.412 3.0 3.314 3.205 3.241 3.318 3.349 3.362 3.375 0.061 4.004 3.867 3.935 4.051 4.136 4.211 4.291 0.287 注:γ2 为连续桥梁单跨跨径20m 时的车辆荷载分项系数。 图4 设计基准期内车辆荷载效应变异系数 随跨径的变化(T=100年) Fig.4 VariationCoefficientofVehicleLoadEffectin DesignReferencePeriodvs.SpanofBridge 的车辆荷载分项系数计算的桥梁结构可靠指标,比 按现行规范中规定的车辆荷载分项系数取1.4计算 的桥梁结构可靠指标更合理。 (4)本文是在固定永久荷载效应分项系数的前 提下,对中、小跨径桥梁结构车辆荷载分项系数的取 值进行了研究,并未考虑永久荷载效应和抗力统计 参数的发展变化。建议在全国范围内开展永久荷载 和抗力统计参数的调研,研究各效应分项系数的取 值,这对现行规范的修订将更具有参考意义。 参考文献: References: [1] 贡金鑫,李文杰,赵 君 黎,等.公路桥梁车辆荷载概率 模型研究(一)———非 治 超 地 区 [J].公 路 交 通 科 技, 2010,27(6):40-45,57. GONGJin-xin,LI Wen-jie,ZHAOJun-li,etal.Re- searchonProbabilisticModelofHighwayBridgeVe- hicleLoads(1)-Non-controllingArea[J].Journalof HighwayandTransportationResearchandDevelop- ment,2010,27(6):40-45,57. [2] 贡金鑫,李文杰,赵 君 黎,等.公路桥梁车辆荷载概率 模型 研 究 (二)———计重收费地区和强制治 超地区 [J].公路交通科技,2010,27(7):56-60. GONGJin-xin,LI Wen-jie,ZHAOJun-li,etal.Re- searchonProbabilisticModelofHighwayBridgeVe- hicleLoads(2)-Toll-by-weightAreaand Overload ControllingArea[J].JournalofHighwayandTrans- portationResearchandDevelopment,2010,27(7):56- 60. [3] LIU Xiao-gang,FANJian-sheng,NIEJian-guo,etal. BehaviorofCompositeRigidFrameBridgeUnderBi- directionalSeismicExcitations[J].JournalofTraffic and Transportation Engineering:English Edition, 2014,1(1):62-71. [4] JTGD60—2004,公路桥涵设计通用规范[S]. JTGD60—2004,GeneralCodeforDesignofHighway BridgesandCulverts[S]. [5] 贡金鑫,杨晓艳,贺 拴 海,等.荷载组合方法与系数的 研究 [R].北 京:中交公路规划设计院有限公司, 2011. GONGJin-xin,YANGXiao-yan,HEShuan-hai,etal. 第6期 杨晓艳,等:不同跨径桥梁车辆荷载分项系数及可靠度 56

65 中国公路学报 2015年 way [ [6】运一新,赵黎,张启伟,等桥梁设计荷我与安全器 荷载的研究[R], 北 ,中交公路规划设计院有限 Theory[J]Chin 11 LU Yi-xin.ZHAO Jum-li.ZHANG Qi-wei.et al.Re [12 WANG Ta.HAN Wa G Fei.et al.Wind Load for Bridae Highway Consu Random Traffic Flow o Traf- .1d201 fie and Tr Engi eering:E Enalish Edi [7]将刚,素权,林道锦.公路桥梁车钙荷我的双峰 2014.14 布率模型0].清华大学学报:自然科学版,203.43 [3]孙蜻.中小跨径梁桥荷载基本组合分项系数研究 10),139+1396.1404 bilistis Model of Highw d Bridgs Vehicle Loads an Bridges[D].Xi'an:Chang'an Univ [14 B5015 2008,公路工程结构可靠度设计统一标准 s] m WIM Datar 1.Engi 1.2002.2 GB501-2008.Unified Standard for Reliability D 81.1071-1084 [ [9】NOWAK A S.Calibration of LRFD ridge断eig [15] 装.工程结构可性设计理[M们.北 Code[M].Washin DC:National Acade my Press 1900 .WEl Wei-wei.Reliability Design The [10]JORDAN P.CHRISTOPHER H.Calibration of LR FD Live Factors Using 。0 on DC:Ore (上接第58页) 103,90 ZHOU Dong-hua.WANG Qiong-fen.FAN Jiang. WU Ming-jun,CHEN Sha et al.A New Method for the Calculation of Reinforee tion of Cireula ment of Concrete:General Dimensionless Designing on Fl ers of Reinfo ete[J] Diagram[J].Engineering Mechanics,2010,27 (1 ) e2010,40 10):102103,9 165-172 [10] [8】陈旭周东华,章胜平,等.压弯截面的弹塑性弯矩 曲率相关关系的解析法[J门.工程力学,2014,31(11): WOM IMELSDORFF O.Reinforced Concrete 175-182,197. sign and Constructor -Part 2:Column l Are CHEN Xu.ZHOU Dong-hua.ZHANG Sheng-ping. Construetion[M].Koln:Fed et al.Analytical Method to Determine the Elasto-plas tie Moment-curvature Relationship of Bending Section [12] JTG D6 4,公路锅筋混凝土及预应力混凝土桥 []Engineering Mechanies.2014.31 (11):175-182 潘设计规范[ 197 JTG D62-2004.Cod e for Design of Highway Reir [9】吴明军,陈少云.解筋混凝士圆形截面受弯构件配金 ncrete and Prestressed Conerete Bridges and 简化计算方法研究[J].建筑结构,2010,40(10):102 Culverts[S]. 1994-2019 China Academie Joumal Electronic Publishing House.All rights reserved.htp://www.enkine
Researchon Load Combination Methodand Coeffi- cient[R].Beijing:CCCC HighwayConsultantsCo., Ltd.,2011. [6] 逯一新,赵君黎,张 启 伟,等.桥梁设计荷载与安全鉴 定荷载的研究[R].北 京:中交公路规划设计院有限 公司,2012. LU Yi-xin,ZHAOJun-li,ZHANG Qi-wei,etal.Re- searchonDesignLoadforBridgeandLoadSecurityI- dentification[R].Beijing:CCCC HighwayConsultants Co.,Ltd.,2012. [7] 梅 刚,秦 权,林道锦.公路桥梁车辆荷载的双峰分 布概率模型[J].清华大学学报:自然科学版,2003,43 (10):1394-1396,1404. MEIGang,QIN Quan,LIN Dao-jin.Bi-modalProba- bilisticModelofHighwayandBridgeVehicleLoads [J].Journalof Tsinghua University:Science and Technology,2003,43(10):1394-1396,1404. [8] MIAOTJ,CHAN T H T.BridgeLiveLoad Models from WIM Data[J].EngineeringStructures,2002,24 (8):1071-1084. [9] NOWAK A S.CalibrationofLRFD Bridge Design Code[M].WashingtonDC:NationalAcademyPress, 1999. [10] JORDAN P,CHRISTOPHER H.CalibrationofLR- FD LiveFactors Using Weigh-in-motion Data[R]. WashingtonDC:Oregon DepartmentofTransporta- tionResearchUnit,2006. [11] 张建仁.基于概率理论的荷载分项系数分析研究[J]. 中国公路学报,1993,6(1):55-60,72. ZHANG Jian-ren.AnalysisofPartialLoad Factors Basedon Probability Theory[J].ChinaJournalof HighwayandTransport,1993,6(1):55-60,72. [12] WANGTao,HAN Wan-shui,YANGFei,etal.Wind- vehicle-bridgeCoupled Vibration AnalysisBasedon RandomTrafficFlowSimulation[J].JournalofTraf- ficandTransportationEngineering:EnglishEdition, 2014,1(4):293-308. [13] 孙 婧.中小跨径梁桥荷载基本组合分项系数研究 [D].西安:长安大学,2011. SUNJing.AnalysisonPartialSafetyFactorofthe LoadsBasicCombinationofSmalland MediumSpan Bridges[D].Xian:ChanganUniveristy,2011. [14] GB50153—2008,公路工程结构可靠度设计统一标准 [S]. GB50153—2008,UnifiedStandardforReliabilityDe- signofHighwayEngineeringStructures[S]. [15] 贡金鑫,魏 巍 巍.工程结构可靠性设计原理 [M].北 京:机械工业出版社,2007. GONGJin-xin,WEIWei-wei.ReliabilityDesignThe- oryfor Engineering Structures[M].Beijing:China MachinePress, 2007. (上接第58页) ZHOU Dong-hua,WANG Qiong-fen,FAN Jiang, etal.ANew MethodfortheCalculationofReinforce- mentofConcrete:GeneralDimensionless Designing Diagram[J].Engineering Mechanics,2010,27(1): 165-172. [8] 陈 旭,周东华,章胜平,等.压弯截面的弹塑性弯矩- 曲率相关关系的解析法[J].工程力学,2014,31(11): 175-182,197. CHEN Xu,ZHOU Dong-hua,ZHANG Sheng-ping, etal.AnalyticalMethodtoDeterminetheElasto-plas- ticMoment-curvatureRelationshipofBendingSection [J].Engineering Mechanics,2014,31(11):175-182, 197. [9] 吴明军,陈少云.钢筋混凝土圆形截面受弯构件配筋 简化计算方法研究[J].建 筑 结 构,2010,40(10):102- 103,90. WU Ming-jun,CHENShao-yun.StudyonSimplified MethodofReinforcementCalculationofCircularSec- tionFlexural MembersofReinforced Concrete[J]. BuildingStructure,2010,40(10):102-103,90. [10] BSEN 1992-1-1,Eurocode2,DesignofConcrete Structures[S]. [11] WOMMELSDORFF O.ReinforcedConcrete- De- signandConstruction-Part2:Column:SpecialAreas ofReinforcedConcreteConstruction[M].Kln:Fed- eralPressLtd.,2011. [12] JTGD62—2004,公路钢筋混凝土及预应力混凝土桥 涵设计规范[S]. JTGD62—2004,CodeforDesignofHighwayRein- forcedConcreteandPrestressedConcreteBridgesand Culverts[S]. 66 中 国 公 路 学 报 2015年