
第月 中国海洋大学学报 PERioDICAL OF OCEAN UNIVERSITY OF CHINA 462g 不同设计使用年限下实用设计表达式系数的求解 蒋济同,吴颖欣,杜德润 (中国海洋大学士木工程系,山东背岛26100) 摘要:基于可靠度分析理论以及荷载标准值等数据的调整,分别运用JCSS法与Monte Carlo法计算出运用于结枸领域 的新的目标可靠指标并依据不同可变荷载的穩常统计模型计算出对应于不同设计使用年限的词整系数及数理统计参数 以最小二乘法为准则,借助Matlab里的数学算子,分别采用穷举优化搜索法和极值理论求解法计算出实用设计表达式中 荷载分项系数及结构重要性系数,并计算出标准值等数帮调整前后的单构件的相对误差增量。从工程实际应用出发,在荷 载,抗力分项系数均按现行规范采用的情况下,计算出能同时体现不同安全等级与设计使用年限的结构重要性系数,并分 析了现行规范中采用的结构重要性系数取值对应的包络范围,对今后结构设计提供参考借整。 关触词:可靠度,安全等级,设计使用年限:分项系数:结构重要性系数 中图法分举号,T1318 文献标志码:A 文章编号:1672-5174(2016)03-121-05 D0l:10.16441/h.cmki.hdxh.2014o192 引用格式:蒋济同,吴颗欣,杜德润。不同设计使用年限下实用设计表达式系数的求解[J门。中国海洋大学学报(自然科 学版),2016.46(3),121-125. JIANG Ji-Tong.WU Ying-Xin.DU De-Run.Solution on the coefficients of design formulation for the pragmatie usage un der different design working lives[]].Periodical of Ocean University of China.2016.46(3):121-125. 《建筑结构设计统 一标准经调查、实测并经数 员习惯于采用基本变量的标准值和分项系数进行结构 理统计处理后,得到了全国范围内水久荷截、可变荷载 设计,使设计表达式所设计出的结构所具有的可靠指 的概率分布函数和统计参数,是中国目前可靠度分析 标尺可能地接所稀定的目标可可堂指标。目前均果用】 的基础。现行的《工程结构可靠性设计统一标准)采 最小二乘法为准则,讲行实用表达式中的分项系数求 用“校准法”确定了今后设计时采用的可靠指标 在校 解,使用分项系数设计 结构时无需进行概率方面的运 准可靠指标B时,考虑了具有代表性的14种构件、不同 算,并已积紫了大量的工程实践经验 的荷载效应比。以及三种简单荷载组合,根据编制标沿 《工程结构可靠性设计原理》)和《土木工程结构 时各随机变量的标准值计算其统计参数,新版《建筑 可靠度理论与设计》)等文献中给出了确定分项系数 结构荷载规范回对中国的结构构件安全度做了调整 的原则和方法。但众多文献推荐的步骤中,是在假定 整体设置水平有所提高,因此可靠指标也应随之改 结构重要性系数 ,已知的前 下运用穷举法进行求 变,提高后的可靠指标与荷兰、丹麦等国家的标准相接 解。这一前提只体现安全等级,无法与《民用建筑 近。 则》幻中321条规定以及《建筑结构可靠性设计较 从简单到复杂或精确程序的不同,国内外先后采 标准)第7.0.3条规 用了一次二阶矩法 阶矩法、蒙特卡洛(Mont 定对应,《结构的设计使用年限与结构重要性系 Caro)等方法进行可靠指标求解。日前行业内广泛牙 数)四,《通用设计表达式中荷载与抗力分项系数的研 用一次二阶矩法中的验算点法和蒙特卡洛法中的重要 究》)等文献中也提到了关于此方面的问题与看法 抽样法进行可靠指标求解。验算点法将非线性功能函 以荷载和抗力的数理模型为基础,系袋求解不同 数作一次叁勒级数展开,并使用当量正态化后的随机 设计使用年限所对应的数理统计参数与实用设计表达 变量平均值和方差进行求解,蒙特卡洛法运用计算 式中相应系数,弥补了目前可靠度研究文献中的不足】 构的失效概率来求解可靠度,对于结构可靠度不高即 针对目前众多文献中采用的穷举求解法的不足,运用 失效概奉较大的情况,有较高的效奉。 Matlab中fminsearch函数,在不改变抗力分项系数y 对于一般的结构构件,若根据规定的B值直接进行 和不提前设定。具体值的前提下,求解出与设计使用 裁面设计或截面复核,计算工作量大且不实用,设计人 年限相匹配的荷载分项系数,a以及结构重要性系 .con 1994-2018 China Academic Joural Electronic Publishing House.All rights reserved http://www.cnki.ne
第46卷 第3期 2016年3月 中 国 海 洋 大 学 学 报 PERIODICALOFOCEAN UNIVERSITYOFCHINA 46(3):121~125 Mar.,2016 不同设计使用年限下实用设计表达式系数的求解 蒋济同,吴颖欣,杜德润 (中国海洋大学土木工程系,山东 青岛 266100) 摘 要: 基于可靠度分析理论以及荷载标准值等数据的调整,分别运用JCSS法与 MonteCarlo法计算出运用于结构领域 的新的目标可靠指标并依据不同可变荷载的概率统计模型计算出对应于不同设计使用年限的调整系数及数理统计参数。 以最小二乘法为准则,借助 Matlab里的数学算子,分别采用穷举优化搜索法和极值理论求解法计算出实用设计表达式中 荷载分项系数及结构重要性系数,并计算出标准值等数据调整前后的单构件的相对误差增量。从工程实际应用出发,在荷 载、抗力分项系数均按现行规范采用的情况下,计算出能同时体现不同安全等级与设计使用年限的结构重要性系数,并 分 析了现行规范中采用的结构重要性系数取值对应的包络范围,对今后结构设计提供参考借鉴。 关键词: 可靠度;安全等级;设计使用年限;分项系数;结构重要性系数 中图法分类号: TU318 文献标志码: A 文章编号: 1672-5174(2016)03-121-05 DOI: 10.16441/j.cnki.hdxb.20140192 引用格式: 蒋济同,吴颖欣,杜德润.不同设计使用年限下实用设计表达式系数的求解[J].中国海洋大学学报(自然科 学版),2016,46(3):121-125. JIANGJi-Tong,WU Ying-Xin,DUDe-Run.Solutiononthecoefficientsofdesignformulationforthepragmaticusageun- derdifferentdesignworkinglives[J].PeriodicalofOceanUniversityofChina,2016,46(3):121-125. 收稿日期:2014-06-10;修订日期:2015-01-12 作者简介:蒋济同(1966-),男,教授。E-mail:baomiaoxinzi@163.com 《建筑结 构 设 计 统 一 标 准》[1]经 调 查、实 测 并 经 数 理统计处理后,得到了全国范围内永久荷载、可变荷载 的概率分布函 数 和 统 计 参 数,是 中 国 目 前 可 靠 度 分 析 的基础。现行的《工程结构可靠性设计统一标准》[2]采 用“校准法”确定了今后设计时采用的可靠指标。在校 准可靠指标β时,考虑了具有代表性的14种构件、不同 的荷载效应比ρ以及三种简单荷载组合,根据编制标准 时各随机变 量 的 标 准 值 计 算 其 统 计 参 数。新 版《建 筑 结构荷载规范》[3]对中国的结构构件安全度做了调整, 整体设置水平 有 所 提 高,因 此 可 靠 指 标β也 应 随 之 改 变,提高后的可靠指标与荷兰、丹麦等国家的标准相接 近。 从简单到复 杂 或 精 确 程 序 的 不 同,国 内 外 先 后 采 用了一次二 阶 矩 法、二 次 二 阶 矩 法、蒙 特 卡 洛(Monte- Carlo)等方法进行可靠指标求解。目前行 业 内 广 泛 采 用一次二阶矩法中的验算点法和蒙特卡洛法中的重要 抽样法进行可靠指标求解。验算点法将非线性功能函 数作一次泰勒 级 数 展 开,并使用当量正态化后的随 机 变量平均值和 方 差 进 行 求 解,蒙 特 卡 洛 法 运 用 计 算 结 构的失效概率 来 求 解 可 靠 度,对 于 结 构 可 靠 度 不 高 即 失效概率较大的情况,有较高的效率。 对于一般的结构构件,若根据规定的β值直接进行 截面设计或截面复核,计算工作量大且不实用,设计人 员习惯于采用基本变量的标准值和分项系数进行结构 设计,使设计表 达 式 所 设 计 出 的 结 构 所 具 有 的 可 靠 指 标尽可能地接近预定的目标可靠指标。目前均采用以 最小二乘法为 准 则,进 行 实 用 表 达 式 中 的 分 项 系 数 求 解,使用分项系 数 设 计 结 构 时 无 需 进 行 概 率 方 面 的 运 算,并已积累了大量的工程实践经验。 《工程结 构 可 靠 性 设 计 原 理》[4]和《土 木 工 程 结 构 可靠度理论与 设 计》[5]等 文 献 中 给 出 了 确 定 分 项 系 数 的原则和方 法。但众多文献推荐的步骤中,是 在 假 定 结构 重 要 性 系 数γ0 已知的前提下运用穷举法进行求 解。这一前 提 只 体 现 安 全 等 级,无 法 与 《民 用 建 筑 通 则》[6]中3.2.1条规定以及《建筑结构可靠性设计统一 标准》[7]第7.0.3条规 定对应,《结构的设计使用年限与结构重要性系 数》[8]、《通用设 计 表 达 式 中 荷 载 与 抗 力 分 项 系 数 的 研 究》[9]等文献中也提到了关于此方面的问题与看法。 以荷载和抗 力 的 数 理 模 型 为 基 础,系 统 求 解 不 同 设计使用年限所对应的数理统计参数与实用设计表达 式中相应系数,弥补了目前可靠度研究文献中的不足。 针对目前众多 文 献 中 采 用 的 穷 举 求 解 法 的 不 足,运 用 Matlab中fminsearch函数,在不改变抗力分项系数γR 和不提前设定γ0 具体值的前提下,求解出与设计使用 年限相匹配的荷载分项系数γG、γQ 以及结构重要性系
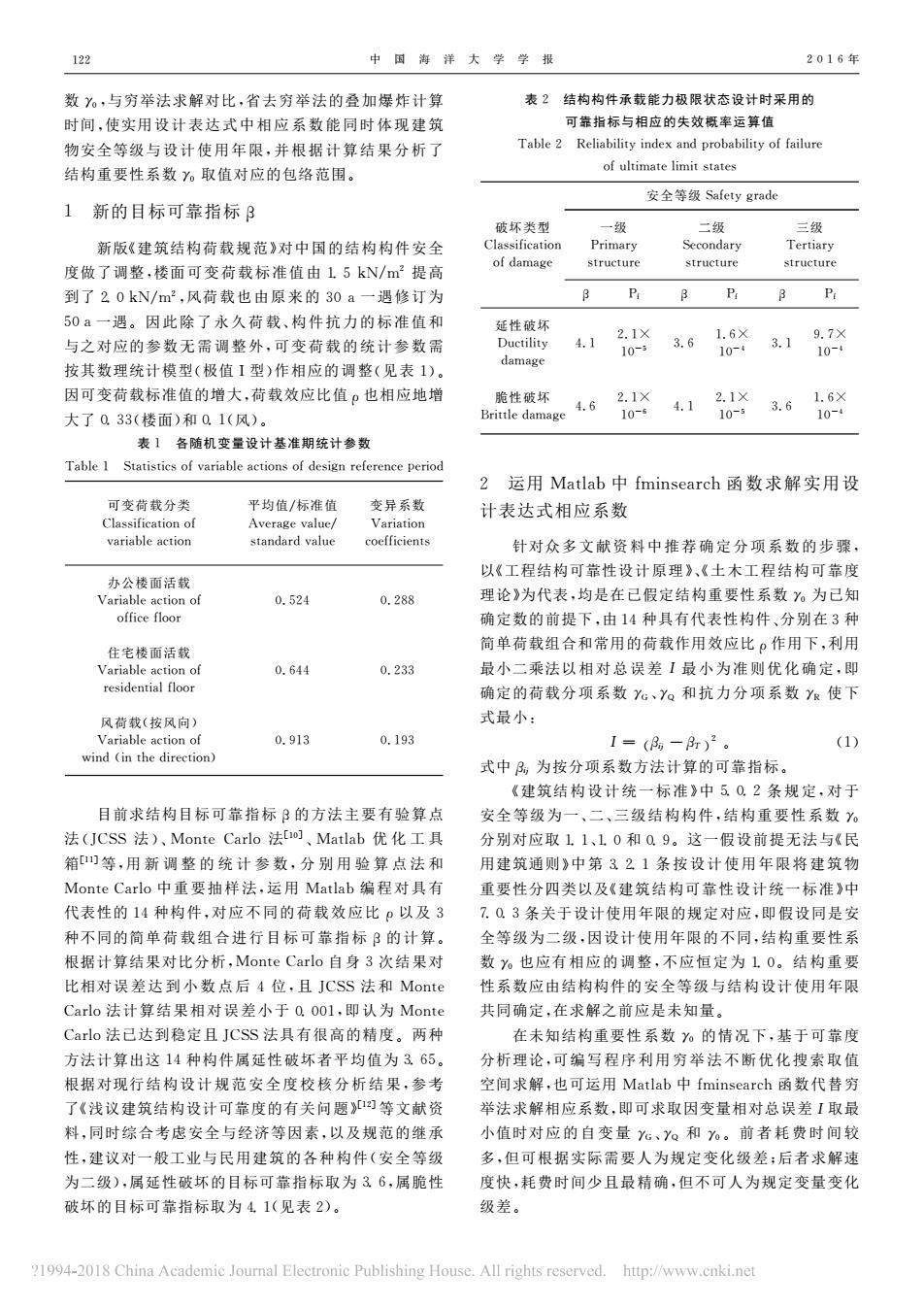
12 中海洋大学学报 2016年 数y。,与穷举法求解对比,省去穷举法的叠加爆推计算 表2结构构件承载能力极限状态设计时采用的 时间,使实用设计表达式中相应系数能同时体现建筑 可靠指标与相应的失效概率运算值 物安全等级与设计使用年限,并根据计算结果分析 Table 2 Reliability index and probability of failure 结构重要性系数%取值对应的包络范围。 of ultimate limit states 安全等级Safety grade 1新的目标可靠指标3 破坏类型 新版。建笛结构荷截却节》对中国的结均构件安全 Secondary 度 了调整,楼面可变荷载标准值由15kN/m提 structure strueture 了20kN/m2,风荷载也由原米的30a 一遇修订为 RP. B P 50a一调。因此除了永久荷裁、构件抗力的标准箱和 与之对应的参数无需调整外,可变荷载的统计参数需 按其新理转计模利(极值】利)作相应的调整见表 因可变荷载标准值的增大,荷载效应比值也相应地站 B脆性酸坏 amage 4.6 41203.65☒ 大了Q33(楼面)和Q1(风) 表】各随机变量设计基准期统计参数 Table 1 Statisties of variable actions of design refer e period 2 运用Matlab中fminsearch函数求解实用设 计表达式相应系数 variable action tandard value coefficient 针对众名文献资料中推荐确定分项系数的步骤 以《工程结构可靠性设计原理》,《土木工程结构可靠度 of 0.524 0.288 理论》为代表,均是在已假定结构重要性系数为已为 office floo 确定数的前提下,由14种具有代表性构件、分别在3种 简单荷载组合和常用的荷载作用效应比。作用下,利用 V住老楼面活 residential floor 0.64 0.233 最小一乘法以相对总误差】最小为准测优化确定,即 确定的荷载分项系数。,Y和抗力分项系数Y使下 风荷规(按风向 式最小 wimd n the i 0.913 0.193 1=(8.-3r12 (1) a) 式中居为按分项系数方法计算的可靠指标 《球结构设计统一标准》中50.2规定,对于 目前求结构目标可靠指标 安全等级为 三级结构构件,结构重要性系数 分别对应取11、10和Q9。这一假设前提无法与《民 箱)等,用新调整的统计参数,分别用验算点法和 用建筑通则》中第321条按设计使用年限将建筑物 Monte carlo中重要抽样法,云用Matlab锦程对且有 重要性分四类以及《建筑结构可常性设计统一标准》中 代表性的14种构件,对应不同的昔载效应比。以及3 7Q3条关于设计使用年限的规定对应,即假设同是安 种不同的简单荷载组合进行目标可靠指标B的计算 全等级为二级 ,因设计使用年限的 同,结构重要性 根据计算结果对比分析,Monte Carlo自身3次结果对 数%也应有相应的调整,不应恒定为10。结构重 比相对误差达到小数点后4位,且JCSs法和Monte 性系数应由结构构件的安全等级与结构设计使用年限 al。法计算结里相计湿差小干0001,即认为M0mt 共同确定,在求解之前应是未知量。 C。法已达到稳定日JCSS法具有很高的精度两种 在未知结构重要性系数%的情况下,基于可靠度 方法计算出这14种构件属延性破坏者平均值为 分析理论,可编写程序利用穷举法不断优化搜索取 根据对现行结构设计规范安全度校核分析结果,参考 空间求解,也可运用Matlab中fminsearch函数代替 了《浅议建筑结构设计可靠度的有关间题》四等文献资 举法求解相应系数,即可求取因变量相对总误差1取最 料,同时综合考虑安全与经济等因素,以及规范的继承 小值时对应的自变量,y。和。。前者耗费时间较 性,建议对一般工业与民用建筑的各种构件(安全等级 多,但可根据实际需要人为规定变化级差:后者求解速 为二级),属延性破坏的目标可靠指标取为36,属脆性 度快,耗费时间少且最精确,但不可人为规定变量变 破坏的目标可靠指标取为41(见表2)。 级左。 1994-2018 China Academic Joumal Electronic Publishing House.All rights reserved.http:/www.enki.ne
中 国 海 洋 大 学 学 报 2016 年 数γ0,与穷举法求解对比,省去穷举法的叠加爆炸计算 时间,使实用设计表达式中相应系数能同时体现建筑 物安全等级与 设 计 使 用 年 限,并 根 据 计 算 结 果 分 析 了 结构重要性系数γ0 取值对应的包络范围。 1 新的目标可靠指标β 新版《建筑结构荷载规范》对中国的结构构件安全 度做了调整,楼面可 变 荷 载 标 准 值 由1.5kN/m2 提 高 到了2.0kN/m2,风荷 载 也 由 原 来 的30a一 遇 修 订 为 50a一遇。因 此 除 了 永 久 荷 载、构 件 抗 力 的 标 准 值 和 与之对应的参 数 无 需 调 整 外,可 变 荷 载 的 统 计 参 数 需 按其数理统计模型(极值I型)作相应的调整(见表1)。 因可变荷载标准值的增大,荷载效应比值ρ也相应地增 大了0.33(楼面)和0.1(风)。 表1 各随机变量设计基准期统计参数 Table1 Statisticsofvariableactionsofdesignreferenceperiod 可变荷载分类 Classificationof variableaction 平均值/标准值 Averagevalue/ standardvalue 变异系数 Variation coefficients 办公楼面活载 Variableactionof officefloor 0.524 0.288 住宅楼面活载 Variableactionof residentialfloor 0.644 0.233 风荷载(按风向) Variableactionof wind(inthedirection) 0.913 0.193 目前求结构目标可靠指标β的方法主要有验算点 法(JCSS 法)、MonteCarlo 法[10]、Matlab 优 化 工 具 箱[11]等,用新调整的统计参数,分别用验算点法和 MonteCarlo中 重 要 抽 样 法,运 用 Matlab编 程 对 具 有 代表性的14种构件,对应 不 同 的 荷 载 效 应 比ρ以 及3 种不同的简单 荷 载 组 合 进 行 目 标 可 靠 指 标 β的 计 算。 根据计算结果对比分析,MonteCarlo自身3次结果对 比相对误 差 达 到 小 数 点 后 4 位,且 JCSS 法 和 Monte Carlo法计算结果相对误差小于0.001,即认为 Monte Carlo法已达到稳定且JCSS法具有很高的精度。两种 方法计算出这14种构件属延性破坏者平均值为3.65。 根据对现行结 构 设 计 规 范 安 全 度 校 核 分 析 结 果,参 考 了《浅议建筑结构设计可靠度的有关问题》[12]等文献资 料,同时综合考虑安全与经济等因素,以及规范的继承 性,建议对一般工业与民用建筑的各种构件(安全等级 为二级),属延性破坏的目标可靠指标取为3.6,属脆性 破坏的目标可靠指标取为4.1(见表2)。 表2 结构构件承载能力极限状态设计时采用的 可靠指标与相应的失效概率运算值 Table2 Reliabilityindexandprobabilityoffailure ofultimatelimitstates 破坏类型 Classification ofdamage 安全等级Safetygrade 一级 Primary structure 二级 Secondary structure 三级 Tertiary structure β Pf β Pf β Pf 延性破坏 Ductility damage 4.1 2.1× 10-5 3.6 1.6× 10-4 3.1 9.7× 10-4 脆性破坏 Brittledamage 4.6 2.1× 10-6 4.1 2.1× 10-5 3.6 1.6× 10-4 2 运用 Matlab中fminsearch函数求解实用设 计表达式相应系数 针对众多文献资料中推荐确定分项系数的步骤, 以《工程结构可靠性设计原理》、《土木工程结构可靠度 理论》为代表,均是在已假定结构重要性系数γ0 为已知 确定数的前提下,由14种具有代表性构件、分别在3种 简单荷载组合和常用的荷载作用效应比ρ作用下,利用 最小二乘法以 相 对 总 误 差I 最 小 为 准 则 优 化 确 定,即 确定的荷载分 项 系 数γG、γQ 和抗力分项系数γR 使 下 式最小: I= ( ) βij -βT 2 。 (1) 式中βij 为按分项系数方法计算的可靠指标。 《建筑结构 设 计 统 一 标 准》中5.0.2条 规 定,对 于 安全等级为一、二、三级结构构件,结构重要性系数γ0 分别对应取1.1、1.0和0.9。这一假设前提无法与《民 用建筑通则》中 第3.2.1条 按 设 计 使 用 年 限 将 建 筑 物 重要性分四类以及《建筑结构可靠性设计统一标准》中 7.0.3条关于设计使用年限的规定对应,即假设同是安 全等级为二级,因设计使用年限的不同,结构重要性系 数γ0 也应有 相 应 的 调 整,不 应 恒 定 为1.0。结 构 重 要 性系数应由结构构件的安全等级与结构设计使用年限 共同确定,在求解之前应是未知量。 在未知结构重要性系数γ0 的情况下,基于可靠度 分析理论,可编 写 程 序 利 用 穷 举 法 不 断 优 化 搜 索 取 值 空间求解,也可运用 Matlab中fminsearch函数代替穷 举法求解相应系数,即可求取因变量相对总误差I取最 小值时对应 的 自 变 量γG、γQ 和γ0。前者耗费时间较 多,但可根据实际需要人为规定变化级差;后者求解速 度快,耗费时间少且最精确,但不可人为规定变量变化 级差。 221
3期 蒋济网,等:不同设计使用年限下实用设计表达式系数的求解 123 在相同前提条件下,将新版《建筑结构荷载规范 0.0s 标准值及重现期调整前后的二级结构构件在设计基准 期为50a的数理统计参数带入程序计算(见图1,2) 0.06 0.04 Q.o2 11 图3调整前后,单构件在不同简单背载组合 图1调整前T-50,1与7,%的关系 作用下相对误差增量 Fig.1 Relationship of I.ye and ya before adjustment Fig.3 Inerease of relative error under different simple load combinations of single member before 3.5 and after adjustment =15 71.4 面可变荷载考虑设计使用年限的调整系数y,使得可 2. 靠度与后续使用年限建立联系。确定楼面可变荷载考 -1.3 虑设计使用年限的调整系数时,可通过可变荷载标 准值校准或通过概率分布函数的校准两种方法确定 本文按照通过概率分布函数的校准确定调整系数九 1.1 1.7 则有 图2调整后T-50.1与ye,y。的关系 Fig.2 Relationship ofIand oafter adjustment n-1+器1n(停)1+a797dln(停) (2 由图可,对干设计使用年限为50a安全等级头 式中:。为可变荷载Q设计基准期最大值的平均值气 二级的结构构件,标准值及重现期调整之前, 标准值的比值:。为可变荷载Q的变异系数。 12、Y。为14,%为1000;经过新版《建筑结构荷载规 根据大量的统计分析,一般假定以上3种可变荷 范》标准值及重现期调整后,即取新的目标可靠指标 载均服从极值1型分布,且设计基准期T内最大荷载 在抗力分项系数y:不变前提下,c为1.3、y。为1.4 分布函数为 %为Q959 Fo.T()-[Fo.(r)]" (3) 由两图中1值可计算出单个构件在每种简单荷载 式中:F。,r(x)为设计基准期可变荷载最大值概率分 组合及荷载效应比值作用情况下的相对误差值,调整 布函数:F,,x)为任意时点的概率分布函数, 前后单构件在不同荷载组合下相对误差分别约为 楼面活荷载可分为楼而持久性荷载和楼而临时性 563%,95%,对出调整前后单构件的相对提差的关 荷载两类,在办公楼楼面活荷载、住宅楼面活荷载保证 值(见图3),可以看出不同构件(依次为枫轴压、偏压 分别为990%和9 4% 设置水平(与现行规范相同 薄钢轴压、偏压,钢筋混凝士轴拉、轴压,大偏压、受弯 下,计算出不同设计使用年限下的楼面荷载取值标准。 受剪、砖石轴压、偏压、受剪、木结构轴压、受弯)在不同 荷载标准值与设计基准期T内的保证率可简化为: 的简单荷载组合下相对误差的增量不同,且调整后的 LkT=4r一0451x lnln(1/p2。(4) 相对误差总体呈现增长趋势,应考虑采用加权求解剑 1.2826 用设计表达式中分项系数和结构重要性系数,以使相 故楼面活荷载的均值和方差可按下列式求解: 对误差控制在允许误差界限内 (5) 不同设计使用年限实用设计表达式中结构 GLT dL (6) 重要性系数优化求解 (7) 《工程结构可靠性设计统一标准》增加了楼面和屋 1994-018 China Academic Joumal Electronic Publishing House.All rights http://www.cnki.net
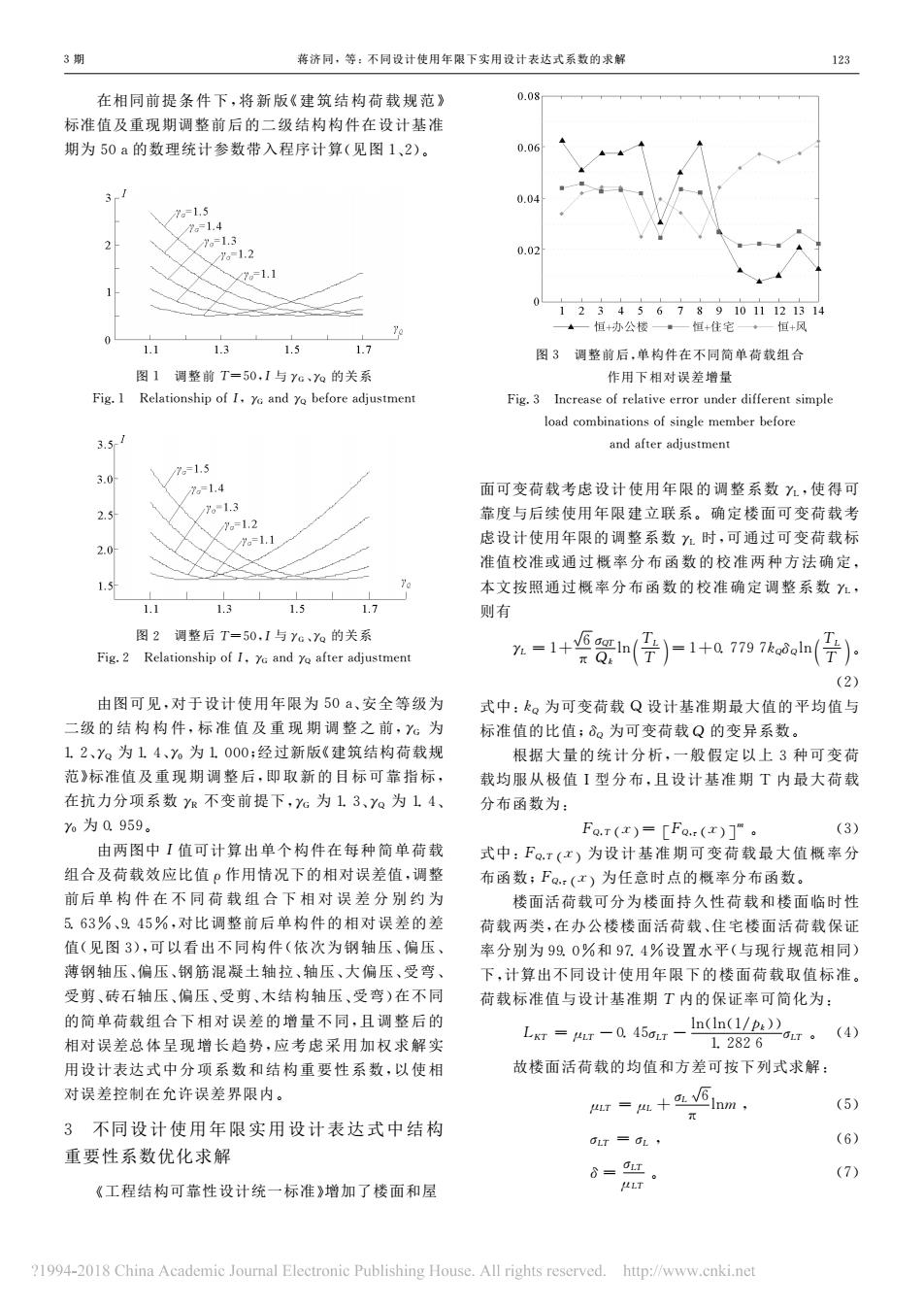
3期 蒋济同,等:不同设计使用年限下实用设计表达式系数的求解 在相同前提 条 件 下,将 新 版《建 筑 结 构 荷 载 规 范》 标准值及重现期调整前后的二级结构构件在设计基准 期为50a的数理统计参数带入程序计算(见图1、2)。 图1 调整前 T=50,I与γG 、γQ 的关系 Fig.1 RelationshipofI,γG andγQ beforeadjustment 图2 调整后 T=50,I与γG 、γQ 的关系 Fig.2 RelationshipofI,γG andγQ afteradjustment 由图可见,对于设计使用年限为50a、安全等级为 二级 的 结 构 构 件,标 准 值 及 重 现 期 调 整 之 前,γG 为 1.2、γQ 为1.4、γ0 为1.000;经过新版《建筑结构荷载规 范》标准值及 重 现 期 调 整 后,即取新的目标可靠指标, 在抗力分项系数γR 不变前提下,γG 为1.3、γQ 为1.4、 γ0 为0.959。 由两图中I值可计算出单个构件在每种简单荷载 组合及荷载效应比值ρ作用情况下的相对误差值,调整 前后单 构 件 在 不 同 荷 载 组 合 下相对误差分别约为 5.63%、9.45%,对比调整前后单构件的相对误差的差 值(见图3),可以看出不同构件(依次为钢 轴 压、偏 压、 薄钢轴压、偏压、钢筋混凝土轴拉、轴压、大偏压、受弯、 受剪、砖石轴压、偏压、受剪、木结构轴压、受弯)在不同 的简单荷载组 合 下 相 对 误 差 的 增 量 不 同,且 调 整 后 的 相对误差总体 呈 现 增 长 趋 势,应 考 虑 采 用 加 权 求 解 实 用设计表达式 中 分 项 系 数 和 结 构 重 要 性 系 数,以 使 相 对误差控制在允许误差界限内。 3 不同设计使用年限实用设计表达式中结构 重要性系数优化求解 《工程结构可靠性设计统一标准》增加了楼面和屋 图3 调整前后,单构件在不同简单荷载组合 作用下相对误差增量 Fig.3 Increaseofrelativeerrorunderdifferentsimple loadcombinationsofsinglememberbefore andafteradjustment 面可变荷载考虑设计使用年 限 的 调 整 系 数γL,使 得 可 靠度与后续使用年限建立联系。确定楼面可变荷载考 虑设计使用年限的调整系数γL 时,可通过可变荷载标 准值校准或通过概率分布函数的校准两种方法确定, 本文按照通过概率分布函数 的 校 准 确 定 调 整 系 数γL, 则有 γL =1+槡6 π σQT Qk ln TL ( ) T =1+0.7797kQδQln TL ( ) T 。 (2) 式中:kQ 为可变荷载 Q 设计基准期最大值的平均值与 标准值的比值;δQ 为可变荷载Q 的变异系数。 根据大 量 的 统 计 分 析,一 般 假 定 以 上3种 可 变 荷 载均服从极值I型分布,且设计基准期 T 内 最 大 荷 载 分布函数为: FQ,T ( )x = FQ,τ ( )[ ] x m 。 (3) 式中:FQ,T ( )x 为设 计 基 准 期 可 变 荷 载 最 大 值 概 率 分 布函数;FQ,τ ( )x 为任意时点的概率分布函数。 楼面活荷载可分为楼面持久性荷载和楼面临时性 荷载两类,在办公楼楼面活荷载、住宅楼面活荷载保证 率分别为99.0%和97.4%设置水平(与现行规范相同) 下,计算出不同设计使用年限下的楼面荷载取值标准。 荷载标准值与设计基准期T 内的保证率可简化为: LKT =μLT -0.45σLT -ln(ln(1/pk)) 1.2826 σLT 。 (4) 故楼面活荷载的均值和方差可按下列式求解: μLT =μL +σL 槡6 π lnm , (5) σLT =σL , (6) δ=σLT μLT 。 (7) 321

124 中海洋大学学报 2016年 式中:r、:分别为设计基准期T内的均值和标准 学模型以及设计基准期内发生超越荷载设计值的概率 一致的原则进行求解,即 (8) 风荷载统计参数求解的基本思想可参照《既有建 式中Q,一和Q工,分别为T1、T:设计基准期下风荷载 筑结构构件的安全性分析[可、《60年设计准期下 最大值概率分布函数 变荷载标准研究】等文献中建议取建筑物的目标使 不问设计使用年限的调整系数九以及数理统计忽 用期作为确定基本风压的重现期,根据极值1型分布数 数(平均值/标准值K,变异系数)的计算结果(见表3)。 表3不同设计使用年限的调整系数及统计参数 Table 3 Adiu and statistics of different design working live 结构设计使用年限Design working life of structure/a action and statistics 10 25 100 0.729 0.811 0.892 0.918 0.940 1.000 1.021 1.055 1.082 办公楼 0.390 037 0.478 0.490l 0.499 0.524 0.531 0543 0.5 0.495 0.407 0.346 0.330 0.318 0.288 0.279 0.266 0.256 老 0.731 0.812 0.893 0.919 0.940 1.00 1.210 1.055 1.08 0.538 0.575 0.607 0.616 0.624 0644 064g 0.658 0.665 0.361 Q310 0.273 0.262 0254 0.233 0.228 0.219 0.212 0.603 0.727 0.846 0.884 0.914 1.000 1.030 1.078 1.115 0.990 0.952 0.93 0.926 922 0.913 0.91 0.907 0.90 (in the direction) 0.296 0.255 0.224 0.216 0.209 0.193 0.188 0.180 0.174 因现行规范仍然采用查载分项系数为12、 由表4可知,在荷载分项系数y。,y。及相应的14 为1.4,及相应14种构件抗力分项系数y。,所以在实用 种构件的抗力分项系数Y均采用现行规范值的情况 设计表达式中的分项系数均不变情况下,采用提高后的 下,对于安全等级为 ,三级结构构件,对于不同 可靠指标(36、41)对不同安全等级以及设计使用年阳 计使用年限,结构重要性系数Y%并非为定值(11,1.0 的结构重要性系数%进行求解,计算结果(见表4)。 Q9),即《维筑结构设计统一标准》中502条规定并 不能包络所有情况,结构重要性系数y。是与结构安全 表4不同安全等级及设计使用年限 等级以及结构设计使用年限成正相关关系。同一安全 等级,设计使用年限为100a的结构构件与设计使用年 and design working lives 限为50a的结构构件相比、设计使用年限为50a的结 设计使用年限 安全等级Safety grad 构构件与设计使用年限为20a的结构构件相比,均相 级 二级 三级 Design working 当于结构安全等级提高一级。 Primary Secondary Tertiary lives/a 现以对结构安 等级为二级的结构构件分析为 structure structure structure 例,若按《建筑结构设计统一标准》中要求对不同设 5 0766 0.687 0617 使用年限均取1.0,对于设计使用年限20a以下结构松 0.790 0.709 件的设计不经济,对于20一50a结构构件偏保守,对于 0.998 0,89 0.80 一60a结构构件较适用,对于60a以上结构构件不 1.018 0.910 0.815 安全。其他不同安全等级对应不同设计使用年限的结 2 106 0.84g 构重要性系数y。也可从 1.127 老4中祖到现行规节中采用的系数的话用带围 1.150 1.02 0.919 目前实际鉴定丁程中经常出现结构抗零能力满 1.198 1.070 0.957 和承载能力不满足的情况,因为《建筑抗震鉴定标 1.241 0.997 准》可中将建筑分为A、B、C类(分为按后续使用30a 1994-2018 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.enki.ne
中 国 海 洋 大 学 学 报 2016 年 式中:μLT 、σLT 分别为设计基准期T 内的均值和标准 差;μL 、σL 分别为任意时点的均值和标准差;m 为设计 基准期T 内荷载平均变动次数。 风荷载统计 参 数 求 解 的 基 本 思 想 可 参 照《既 有 建 筑结构构件的安全性分析》[13]、《60年设计基准期下可 变荷载标准研究》[14]等文献中建议取建筑物的目标使 用期作为确定基本风压的重现期,根据极值I型分布数 学模型以及设计基准期内发生超越荷载设计值的概率 一致的原则进行求解,即 FQ,T1 (QT1,k)=FQ,T2 (QT2,k)。 (8) 式中QT1,k和QT2,k分别为T1 、T2 设计基准期下风荷载 最大值概率分布函数。 不同设计使用年限的调整系数γL 以及数理统计参 数(平均值/标准值 K,变异系数δ)的计算结果(见表3)。 表3 不同设计使用年限的调整系数及统计参数 Table3 Adjustmentfactorsandstatisticsofdifferentdesignworkinglives 活荷载类型及参数 Classificationofvariable actionandstatistics 结构设计使用年限 Designworkinglifeofstructure/a 5 10 20 25 30 50 60 80 100 办公楼 Office γL 0.729 0.811 0.892 0.918 0.940 1.000 1.021 1.055 1.082 K 0.390 0.437 0.478 0.490 0.499 0.524 0.531 0.543 0.553 δ 0.495 0.407 0.346 0.330 0.318 0.288 0.279 0.266 0.256 住宅 Residence γL 0.731 0.812 0.893 0.919 0.940 1.000 1.210 1.055 1.081 K 0.538 0.575 0.607 0.616 0.624 0.644 0.649 0.658 0.665 δ 0.361 0.310 0.273 0.262 0.254 0.233 0.228 0.219 0.212 风 (按风向) Wind (inthedirection) γL 0.603 0.727 0.846 0.884 0.914 1.000 1.030 1.078 1.115 K 0.990 0.952 0.931 0.926 0.922 0.913 0.911 0.907 0.904 δ 0.296 0.255 0.224 0.216 0.209 0.193 0.188 0.180 0.174 因现行规范仍然采用荷载分项系数γG 为1.2、γQ 为1.4,及相应14种构件抗力分项系数γR,所以在实用 设计表达式中的分项系数均不变情况下,采用提高后的 可靠指标(3.6、4.1)对不同安全等级以及设计使用年限 的结构重要性系数γ0 进行求解,计算结果(见表4)。 表4 不同安全等级及设计使用年限γ0 Table4 Coefficientsofimportanceofdifferentsafetygrades anddesignworkinglives 设计使用年限 Designworking lives/a 安全等级Safetygrade 一级 Primary structure 二级 Secondary structure 三级 Tertiary structure 5 0.766 0.687 0.617 10 0.883 0.790 0.709 20 0.998 0.893 0.800 25 1.018 0.910 0.815 30 1.061 0.949 0.849 50 1.127 1.007 0.901 60 1.150 1.027 0.919 80 1.198 1.070 0.957 100 1.241 1.115 0.997 由表4可知,在荷载分项系数γG、γQ 及相应的14 种构件的抗力 分 项 系 数γR 均 采 用 现 行 规 范 值 的 情 况 下,对于安全等级为一、二、三级结构构件,对于不同设 计使用年限,结构重要性系数γ0 并非为定值(1.1、1.0、 0.9),即《建筑 结 构 设 计 统 一 标 准》中5.0.2条 规 定 并 不能包络所有情况,结构重要性系数γ0 是与结构安全 等级以及结构设计使用年限成正相关关系。同一安全 等级,设计使用年限为100a的结构构件与设计使用年 限为50a的结构构件相比、设计使用年限为50a的结 构构件与设计使用年限为20a的 结 构 构 件 相 比,均 相 当于结构安全等级提高一级。 现以对结构安全等级为二级的结构构件分析为 例,若按《建筑 结 构 设 计 统 一 标 准》中要求对不同设计 使用年限均取1.0,对于设计使用年限20a以下结构构 件的设计不经济,对于20~50a结构构件偏保守,对于 50~60a结构构件较适用,对 于60a以上结构构件不 安全。其他不同安全等级对应不同设计使用年限的结 构重要性系数γ0 也可从 表4中得到现行规范中采用的系数的适用范围。 目前实际鉴定工程中经常出现结构抗震能力满足 和承载 能 力 不 满 足 的 情 况,因 为 《建 筑 抗 震 鉴 定 标 准》[15]中将建筑分为 A、B、C类(分为按后续使用30a、 421

3期 蒋济同,等:不同设计使用年限下实用设计表达式系数的求解 125 40a、50a进行抗震鉴定),而承载力方面均按50a的荷 [)杨伟军,赵作智 土木工程结构可靠度理论与设计[门.北京:人 载考虑。 表4中的内容很好地使鉴定工作中的抗震和承费 力相对应,例如 一栋A类建筑,在抗震考虑后续使用年 Press.1999. 限30a的基础上,承载力方面也可按30a的荷载系数 [6们国家标准委员会.G50352-2005民用建筑设计酒则[5】.就京, 加载,使鉴定工作更加合理, 建筑工业出版社,2005 4结论 le for design o (I)根据现行规范数据的调整,运用JCSS法与Mont。 [们国家标准委员会.G肠006g201建筑结构可率性设计统一标准 Calo法求解的结构目标可靠指标3均应在现行规范 [S].北京:由筑工业出版社,200L. (32,37)的基础上提高Q4,相当于失效概率降低 National Standard of Chima.GB506-001(001). 个数量级: ard for reliability design of building structures[S].Beijing:Chin (2)将计算出的不同设计使用年限的调整系数以及数 理统计参数运用带入Maab程序中计算,比较得出 [8 重要性系数[、建筑科学 fminsearch函数编程较穷举优化搜素法速度更快且精 Shi Z H.On Structural Design Working Life and the Importane 确: of Structure 1.Building Science.2000.16(6):32-33. (3)日前规范在可靠指标B采用(32、37)前提下,规定 [9]粪玄平.通用设计表达式中荷载与抗力分项系数的研究D].西 实用设计表达式中 和%分别为12、14和 安:西安建料技大字,200 用设计表达式中:,Y%和%分别为L3、14和 :2006. Q959。根据相对总误差I值可计算出调整前后的单构 [10]董拖秋.田敏博.堂特卡洛法结构可常性分析,黑龙江工程学 件的相对误差分别为563%、945%,且目标可靠指标 院学报.2010(1):27-29. 调整后的相对误差总体呈增长趋势 DONG Yan qiu.TIAN Jing bo.Struetural reliability analysis o (④)在。。和%均采用现行规范值的情况下,求解 Monte Carlo method L JJ.Journal of Heilongjiang Institute o 出结构重要性系数。,计算结果表明不同安全等级及 ]张高峰,质助,张大.应用Mtb优化工具箱求解可靠度同 设计使用年限%应采用不同的数值,并对应总结出规 范中结构重要性系数较适用于50一60a结构构件设 Zhang Gaofeng.Jia Jianxun.Zhang Dawei.Solve reliability prob 计。 emwith matlaboptimization ooEnginering Geology ter Application.2004(1):5-7 参考文献: [12 [】中国建筑科学所究院,建筑结构设计统一标准[S].北京:中国建 ehlkcnodcretihiyofbuidine 筑工业出版社: ,GB6-81 structure design Building Structure.2011():11-15. [13】顾样林,许明,张伟平.既有建筑结构构件的安全性分析[J几。建 essl.Bei Press.1984 筑结构学报,2005,25(6),117122 Safety analysis of structura [2匀】国客标准委员会.G50153-2008工程结构可靠性设计统一标准 ures [S].北京:中国建筑工业出版社,1984. 2005.256,117-122 dard of China.GB Unified stadard fo 14】王凯.吕令段,周建章,等.60年设计基准期下可变荷载标准研 ring structures[S].Beijing:China Ar 究CU门.工程建设与设计,2009(10):19-22. Wang K.LV Ling yi.ZHOU Jian zhang,et al.Studyon the vari [3】国家标准委员会.G50092012定筑构荷我规范[S.北京:中 able load in 60-year design reference period[].Construction 回建疯工业出板社,1984. National Standard of China.GB50009-2012.Load code for the de ,.200910:1r 建筑抗震整定标准[S】。家 sign of building sur]Beiing:China Architecture 速筑工业出板社,2005 g Pres: 201 National Standsrd of China GB50023-2009.Standard for seismi 程结构可靠性设计原理[.北京:机工业 of buildingL5]Beijing:Chin Architecture Blding Press.2009. n.Wei Weiwei.Principle of engine (下转第133页 bility designt M.Beiiing:Machinery Industry Press.2007. 1994-2018 China Aeademic Joumal Electronic Publishing House.All rights reserved. http://www.cnki.net
3期 蒋济同,等:不同设计使用年限下实用设计表达式系数的求解 40a、50a进行抗震鉴定),而承载力方面均按50a的荷 载考虑。 表4中的内容很好地使鉴定工作中的抗震和承载 力相对应,例如一栋 A 类建筑,在抗震考虑后续使用年 限30a的基础上,承载力方面也可按30a的荷载系数 加载,使鉴定工作更加合理。 4 结论 (1)根据现行规范数据的调整,运用JCSS法与 Monte Carlo法求解的结构目标可靠指标β均应在现行规范 (3.2、3.7)的基础上提高0.4,相当于失效概率降低一 个数量级; (2)将计算出的不同设计使用年限的调整系数以及数 理统 计 参 数 运 用 带 入 Matlab 程 序 中 计 算,比 较 得 出 fminsearch函数编程较穷举优化搜索法速度更快且 精 确; (3)目前规范在可靠指标β采用(3.2、3.7)前提下,规定 实用 设 计 表 达 式 中 γG、γQ 和 γ0 分 别 为 1.2、1.4 和 1.0。按照新的目标可靠指标β(即3.6、4.1)求解出实 用设 计 表 达 式 中 γG、γQ 和 γ0 分 别 为 1.3、1.4 和 0.959。根据相对总误差I值可计算出调整前后的单构 件的相对误差分别为5.63%、9.45%,且目标可靠指标 调整后的相对误差总体呈增长趋势; (4)在γG、γQ 和γR 均 采 用 现 行 规 范 值 的 情 况 下,求 解 出结构重要性系 数γ0,计算结果表明不同安全等级及 设计使用年限γ0 应采用不同的数值,并对应总结出规 范中结构重要 性 系 数 较 适 用 于 50~60a结 构 构 件 设 计。 参考文献: [1] 中国建筑科学研究院.建筑结构设计统一标准[S].北 京:中 国 建 筑工业出版社,1984.GBJ68-84. NationalStandardofChina.GBJ68-84,Unifiedstandardsforthe designofstructures[S].Beijing:China Architecture & Building Press,1984. [2] 国家标准 委 员 会.GB50153-2008工程结构可靠性设计统一标准 [S].北京:中国建筑工业出版社,1984. NationalStandardofChina,GB50153-2008,Unifiedstandardfor reliabilitydesignofengineeringstructures[S].Beijing:ChinaAr- chitecture& BuildingPress,2008. [3] 国家标准委员会.GB50009-2012建筑结构荷载规范[S].北京:中 国建筑工业出版社,1984. NationalStandardofChina.GB50009-2012,Loadcodeforthede- signofbuildingstructures[S].Beijing:China Architecture & BuildingPress,2012. [4] 贡金鑫,魏巍巍.工程结构可靠性设计原理[M].北京:机械工业 出版社,2007. GongJinxin,WeiWeiwei.Principleofengineeringstructurerelia- bilitydesign[M].Beijing:MachineryIndustryPress,2007. [5] 杨伟军,赵传智.土木工程结构可靠度理论与设计[M].北京:人 民交通出版社,1999. YangWeijun,ZhaoChuanzhi.ReliabilityTheoryanddesignofciv- ilengineering structures[M ].Beijing:China Communication Press,1999. [6] 国家标准委员会.GB50352—2005民用建筑设计通则[S].北 京: 建筑工业出版社,2005. NationalStandardofChina.GB50352-2005,Codefordesignof civilbuildings[S].Beijing:ChinaArchitecture& BuildingPress, 2005. [7] 国家标准 委 员 会.GB50068-2001建 筑 结 构 可 靠 性 设 计 统 一 标 准 [S].北京:建筑工业出版社,2001. NationalStandardofChina.GB50068-2001(2001),Unifiedstand- ardforreliabilitydesignofbuildingstructures[S].Beijing:China Architecture& BuildingPress,2001. [8] 史志华.结构的设计使用年限与结构重要性系数[J].建 筑 科 学, 2000,16(6):32-33. ShiZH.OnStructuralDesign WorkingLifeandtheImportance FactorofStructure[J].BuildingScience,2000,16(6):32-33. [9] 龚云平.通用设计表达式中荷载与抗力分项系数的研究[D].西 安:西安建筑科技大学,2006. GongYunping.AnalysisonLoadandResistanceFactorsinGener- alDesignExpression[D].Xi′an:XianUniversityofArchitecture andTechnology,2006. [10] 董艳秋,田敬博.蒙特卡洛法结构可靠性分析[J].黑龙江工程学 院学报,2010(1):27-29. DONGYanqiu,TIANJingbo.Structuralreliabilityanalysisof MonteCarlo method[J].Journalof HeilongjiangInstituteof Technology,2010(1):27-29. [11] 张高峰,贾建勋,张大巍.应用 Matlab优化工具箱求解可靠度问 题[J].工程地质计算机应用,2004(1):5-7. ZhangGaofeng,JiaJianxun,ZhangDawei.Solvereliabilityprob- lem with matlaboptimizationtoolbox[J].Engineering Geology ComputerApplication,2004(1):5-7. [12] 张周.浅议建筑结构设计可靠度的有关问题 [J].建 筑 结 构, 2011(2):11-15. ZhangZ.Argumentonrelevantproblemofcredibilityofbuidling structuredesign[J].BuildingStructure,2011(2):11-15. [13] 顾祥林,许勇,张伟平.既有建筑结构构件的安全性分析[J].建 筑结构学报,2005,25(6):117-122. XianglinGU,YongXU,Zhang W.Safetyanalysisofstructural membersofexistingbuildings[J].JournalofBuildingStructures, 2005,25(6):117-122. [14] 王凯,吕令毅,周建章,等.60 年设计基准期下可变荷载标准研 究[J].工程建设与设计,2009(10):19-22. WangK,LVLingyi,ZHOUJianzhang,etal.Studyonthevari- ableloadin60-yeardesignreferenceperiod[J].Construction & DesignforProject,2009(10):19-22. [15] 国家标准委 员 会.GB50023-2009 建筑抗震鉴定标准[S].北 京: 建筑工业出版社,2005. NationalStandardofChina.GB50023-2009,Standardforseismic appraiserofbuilding[S].Beijing:ChinaArchitecture& Building Press,2009. (下转第133页) 521

于,等:结合是著性与GabCt的无角毛类浮植物是微图像分制 ance for the microscopic images with different species and scene complexity,and have strong robustness to resist noise interference.Especially for the phytoplankton image s with the cingulum or sulcus,the seg mentation mon methods on microscopic image segmentation of non-setae phytoplankton species.and can realize real time and irsitu automatic processing of massive sample images, Key words:phytoplankton:microscopic image segmentation:saliency map:GrabCut 责任编辑陈呈超 (上接第125页) Solution on the Coefficients of Design Formulation for the Pragmatic Usage Under Different Design Working Lives JIANG Ji-Tong.WU Ying-Xin.DU De-Run (Department of Civil Engineering.Ocean University of China.Qingdao 266100.China Abstract:Based on the reliability analysis theory and the adjusted characteristic values of an action,the new target reliability index.which is applied in structure area.is calculated using the icss method and Monte Carlo method.Moreover,the adjustment factors and mathematical statistics paramet ers corre sponding to different design working lives are computed according to different probability distribution models of variable actions.Especially.in theoretical analysis.based on the least square method,the par- tial factors of safety for load and the coefficients for importance of structures were developed by using the method of enumeration in association with optimization search and the method of extremum theory respec tively with the function of Matlab.The relative erro increments of the single component are then so before and after the adjustment of the data (e.g.characteristic values).As for practical applications,the different coefficients for importance of structures corresponding to different levels of safety and design working lives under various situations are obtained when the partial safety factor for load and the partial safety factor for resistance meet the requirements of the current standard.Finally,the application envelops Key words:degree of reliability:safety class;design working life;partial safety factor;coefficient for importance of a structure 责任编辑陈里超 1994-2018 China Academic Joural Electronic Publishing House.All rights reserved.http://www.enki.net
3期 于 堃,等:结合显著性与 GrabCut的无角毛类浮游植物显微图像分割 anceforthemicroscopicimageswithdifferentspeciesandscenecomplexity,andhavestrongrobustnessto resistnoiseinterference.Especiallyforthephytoplanktonimageswiththecingulumorsulcus,theseg- mentationaccuracyisveryhigh.Overall,non-interactiveGrabCutobviouslyoutperformstheothercom- monmethodsonmicroscopicimagesegmentationofnon-setaephytoplanktonspecies,andcanrealizereal- timeandin-situautomaticprocessingofmassivesampleimages. Keywords: phytoplankton;microscopicimagesegmentation;saliencymap;GrabCut 责任编辑 陈呈超 (上接第125页) SolutionontheCoefficientsofDesignFormulationforthePragmaticUsage UnderDifferentDesignWorkingLives JIANGJi-Tong,WU Ying-Xin,DU De-Run (DepartmentofCivilEngineering,OceanUniversityofChina,Qingdao266100,China) Abstract: Basedonthereliabilityanalysistheoryandtheadjustedcharacteristicvaluesofanaction,the newtargetreliabilityindex,whichisappliedinstructurearea,iscalculatedusingtheJCSSmethodand MonteCarlo method.Moreover,theadjustmentfactorsand mathematicalstatisticsparameterscorre- spondingtodifferentdesign workinglivesarecomputedaccordingtodifferentprobabilitydistribution modelsofvariableactions.Especially,intheoreticalanalysis,basedontheleastsquaremethod,thepar- tialfactorsofsafetyforloadandthecoefficientsforimportanceofstructuresweredevelopedbyusingthe methodofenumerationinassociationwithoptimizationsearchandthemethodofextremumtheoryrespec- tivelywiththefunctionofMatlab.Therelativeerrorincrementsofthesinglecomponentarethensolved beforeandaftertheadjustmentofthedata(e.g.characteristicvalues).Asforpracticalapplications,the differentcoefficientsforimportanceofstructurescorrespondingtodifferentlevelsofsafetyanddesign workinglivesundervarioussituationsareobtainedwhenthepartialsafetyfactorforloadandthepartial safetyfactorforresistancemeettherequirementsofthecurrentstandard.Finally,theapplicationenvelops ofdifferentcoefficientsforimportanceofstructuresareanalyzedforthefuturestructuredesign. Keywords: degreeofreliability;safetyclass;designworkinglife;partialsafetyfactor;coefficientfor importanceofastructure 责任编辑 陈呈超 331