
第14卷第6期 大学化学 1999年12月 师生笔谈 芳香过渡态理论及其在协同反应中的应用 王红明 (九江师范专科学校化学系江西33200) 在通常的有机化学书中,协同反应都是应用前沿轨道理论或能级相关理论来进行解释,而 很少涉及芳香过渡态理论。其实芳香过波态理论还是有许多可行之处的,特别是对分子轨道 没有任何对称性的协同反应,应用能级相关理论无法解释时,采用该理论能得到满意的解释。 芳香过渡态理论建立在Dewar理论和方nmerman理论基础上,它把所有环状π电子系分 为两大体系山I:HUckel体系和Mobius体系。如一个大环π电子体系经过零次或偶数次的扭 转,即出现零次或偶数次的符号改变,称之为Hckl体系;若环状π电子系出现的是奇数次的 扭转.则称之为Mobius体系。 按照分子轨道理论2l:如在HOckel体系中,含有4g+2个r电子时,表现出极强的稳定 性,则称为芳香性的Hck如l体系,若含有4g个”电子时,则很不稳定,被称为反芳香性的 HUckel体系。在M6bius体系中与此相反,若含有4g个π电子时,则表现极强的稳定性,当含 有4q+2个电子时,稳定性却很差,它们分别被称为芳香性的66ius体系和反芳香性的 M6bius体系,如图1。 0&9 9R 86 (e) 图1 Dckel和M6bis体系示例 (a)符号改变次数为0,电子数4g+2=6,芳香性的Hk如体系 (b)符号改变次数为0,电子数4g=4,反芳香性的Hck体系 (⊙)符号改变次数为1,电子数4g+2=6,反芳香性的M6us体系 (@符号改变次数为1,电子数4g=4,芳香性的6s体系 芳香过渡态理论认为:一个协同反应能形成具有芳香性的过渡态,则可在加热的条件下进 行,若能形成反芳香性的过渡态,则此反应须在光照的条件下才能进行。这就是DewarZim merman规则)。 为什么芳香性的过渡态能在加热的条件下发生,而反芳香性的过渡态则须在光照的条件 下进行呢?下面以丁二烯的顺旋和对旋为例,用定量的计算来对其进行说明。 无论在丁二烯的顺旋还是对旋过程中,只有C和C的2轨道发生扭转,设转角为中,且 令CC2CCC2C间严轨道的作用能为B。在扭转过程中CCCC间轨道的 45 94-2008 China Academie Joumal Electronie Publishing House.All rights reserved.http://www.cnki.net
第 14 卷 第 6 期 大学化学 1999 年 12 月 师生笔谈 芳香过渡态理论及其在协同反应中的应用 王 红 明 (九江师范专科学校化学系 江西 332000) 在通常的有机化学书中 ,协同反应都是应用前沿轨道理论或能级相关理论来进行解释 ,而 很少涉及芳香过渡态理论。其实芳香过渡态理论还是有许多可行之处的 ,特别是对分子轨道 没有任何对称性的协同反应 ,应用能级相关理论无法解释时 ,采用该理论能得到满意的解释。 芳香过渡态理论建立在 Dewar 理论和 Zimmerman 理论基础上 ,它把所有环状π电子系分 为两大体系[1 ] : Hückel 体系和 MÊbius 体系。如一个大环 π电子体系经过零次或偶数次的扭 转 ,即出现零次或偶数次的符号改变 ,称之为 Hückel 体系 ;若环状π电子系出现的是奇数次的 扭转 ,则称之为 MÊbius 体系。 按照分子轨道理论[2 ] :如在 Hückel 体系中 ,含有 4 q + 2 个 π电子时 ,表现出极强的稳定 性 ,则称为芳香性的 Hückel 体系 ,若含有 4 q 个π电子时 ,则很不稳定 ,被称为反芳香性的 Hückel 体系。在 MÊbius 体系中与此相反 ,若含有 4 q 个π电子时 ,则表现极强的稳定性 ,当含 有 4 q + 2 个 π电子时 ,稳定性却很差 ,它们分别被称为芳香性的 MÊbius 体系和反芳香性的 MÊbius 体系 ,如图 1。 图 1 Hückel 和 MÊbius 体系示例 (a) 符号改变次数为 0 ,电子数 4q + 2 = 6 ,芳香性的 Hückel 体系 (b) 符号改变次数为 0 ,电子数 4q = 4 ,反芳香性的 Hückel 体系 (c) 符号改变次数为 1 ,电子数 4q + 2 = 6 ,反芳香性的 MÊbius 体系 (d) 符号改变次数为 1 ,电子数 4q = 4 ,芳香性的 MÊbius 体系 芳香过渡态理论认为 :一个协同反应能形成具有芳香性的过渡态 ,则可在加热的条件下进 行 ,若能形成反芳香性的过渡态 ,则此反应须在光照的条件下才能进行。这就是 Dewar2Zim2 merman 规则[3 ] 。 为什么芳香性的过渡态能在加热的条件下发生 ,而反芳香性的过渡态则须在光照的条件 下进行呢 ? 下面以丁二烯的顺旋和对旋为例 ,用定量的计算来对其进行说明。 无论在丁二烯的顺旋还是对旋过程中 ,只有 C1 和 C4 的 pz 轨道发生扭转 ,设转角为 < ,且 令 C1 —C2、C3 —C4、C2 —C3 间 pz 轨道的作用能为β。在扭转过程中 C1 —C2、C3 —C4 间 pz 轨道的 54
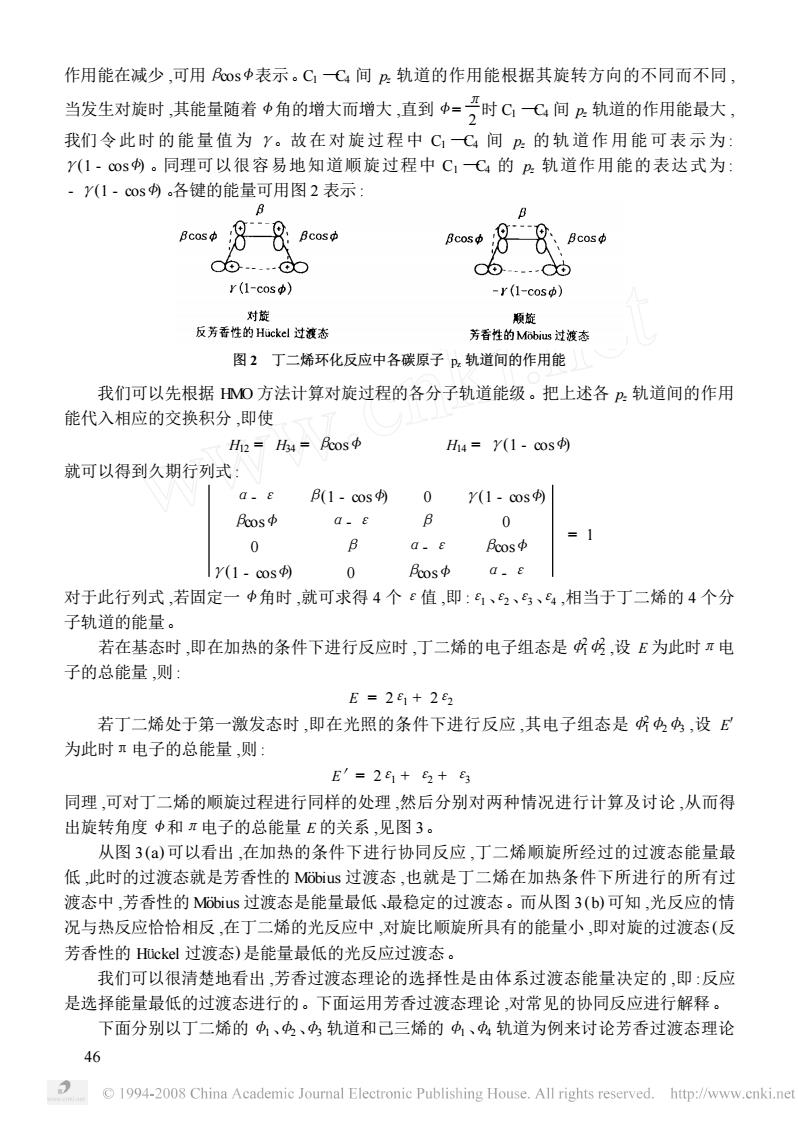
作用能在减少,可用民0s中表示。CC4间2轨道的作用能根据其旋转方向的不同而不同 当发生对旋时,其能量随着中角的增大而增大,直到中=时C(间户轨道的作用能最大, 我们令此时的能量值为y。故在对旋过程中C,C间B的轨道作用能可表示为: Y(1·c®s内。同理可以很容易地知道顺旋过程中C,C的?轨道作用能的表达式为: ·Y(1·cos。各键的能量可用图2表示: 、Bcos中 c6.…d0 06 r(1-cos) -r(l-cos) 反芳香性的Hckl过液态 图2丁二烯环化反应中各碳原子,轨道间的作用能 我们可以先根据MO方法计算对旋过程的各分子轨道能级。把上述各P轨道间的作用 能代入相应的交换积分,即使 =h4=民os中 H4=Y(1-cos) 就可以得到久期行列式: 0.E B(1-cos 0 Y(1-cos Fos中 G-E B 0 =1 0 B a.E 民os中 y(1-cos) 0 os中a.e 对于此行列式,若固定一中角时,就可求得4个ε值,即:6、2、马、,相当于丁二烯的4个分 子轨道的能量 若在基态时,即在加热的条件下进行反应时,丁二烯的电子组态是所号,设E为此时π电 子的总能量,则 E=2e1+282 若丁二烯处于第一激发态时,即在光照的条件下进行反应,其电子组态是4中,设E 为此时电子的总能量,则」 E′=2+5+ 同理,可对丁二烯的顺旋过程进行同样的处理,然后分别对两种情况进行计算及讨论,从而得 出旋转角度中和π电子的总能量E的关系,见图3。 从图3(a)可以看出,在加热的条件下进行协同反应,丁二烯顺旋所经过的过渡态能量最 低,此时的过渡态就是芳香性的Mus过渡态,也就是丁二烯在加热条件下所进行的所有过 渡态中,芳香性的Mus过渡态是能量最低、最稳定的过渡态。而从图3(b)可知,光反应的情 况与热反应恰恰相反,在丁二烯的光反应中,对旋比顺旋所具有的能量小,即对旋的过渡态(反 芳香性的Huckel过渡态)是能量最低的光反应过渡态。 我们可以很清楚地看出,芳香过渡态理论的选择性是由体系过渡态能量决定的,即:反应 是选择能量最低的过渡态进行的。下面运用芳香过渡态理论,对常见的协同反应进行解释。 下面分别以丁二烯的中、中、中轨道和己三烯的中、中轨道为例来讨论芳香过渡态理论 1994-2008 China Academic Joural Electronic Publishing House.All rights reserved.http:/www.enki.ne
作用能在减少 ,可用βcos <表示。C1 —C4 间 pz 轨道的作用能根据其旋转方向的不同而不同 , 当发生对旋时 ,其能量随着 <角的增大而增大 ,直到 < = π 2 时 C1 —C4 间 pz 轨道的作用能最大 , 我们令此时的能量值为 γ。故在对旋过程中 C1 —C4 间 pz 的轨道作用能可表示为 : γ(1 - cos <) 。同理可以很容易地知道顺旋过程中 C1 —C4 的 pz 轨道作用能的表达式为 : - γ(1 - cos <) 。各键的能量可用图 2 表示 : 图 2 丁二烯环化反应中各碳原子 pz 轨道间的作用能 我们可以先根据 HMO 方法计算对旋过程的各分子轨道能级。把上述各 pz 轨道间的作用 能代入相应的交换积分 ,即使 H12 = H34 = βcos < H14 = γ(1 - cos <) 就可以得到久期行列式 : α- ε β(1 - cos <) 0 γ(1 - cos <) βcos < α- ε β 0 0 β α- ε βcos < γ(1 - cos <) 0 βcos < α- ε = 1 对于此行列式 ,若固定一 <角时 ,就可求得 4 个ε值 ,即 :ε1、ε2、ε3、ε4 ,相当于丁二烯的 4 个分 子轨道的能量。 若在基态时 ,即在加热的条件下进行反应时 ,丁二烯的电子组态是φ2 1φ2 2 ,设 E 为此时π电 子的总能量 ,则 : E = 2ε1 + 2ε2 若丁二烯处于第一激发态时 ,即在光照的条件下进行反应 ,其电子组态是φ2 1φ2φ3 ,设 E′ 为此时π电子的总能量 ,则 : E′= 2ε1 + ε2 + ε3 同理 ,可对丁二烯的顺旋过程进行同样的处理 ,然后分别对两种情况进行计算及讨论 ,从而得 出旋转角度 <和π电子的总能量 E 的关系 ,见图 3。 从图 3 (a) 可以看出 ,在加热的条件下进行协同反应 ,丁二烯顺旋所经过的过渡态能量最 低 ,此时的过渡态就是芳香性的 MÊbius 过渡态 ,也就是丁二烯在加热条件下所进行的所有过 渡态中 ,芳香性的 MÊbius 过渡态是能量最低、最稳定的过渡态。而从图 3 (b) 可知 ,光反应的情 况与热反应恰恰相反 ,在丁二烯的光反应中 ,对旋比顺旋所具有的能量小 ,即对旋的过渡态(反 芳香性的 Hückel 过渡态) 是能量最低的光反应过渡态。 我们可以很清楚地看出 ,芳香过渡态理论的选择性是由体系过渡态能量决定的 ,即 :反应 是选择能量最低的过渡态进行的。下面运用芳香过渡态理论 ,对常见的协同反应进行解释。 下面分别以丁二烯的φ1、φ2、φ3 轨道和己三烯的φ1、φ4 轨道为例来讨论芳香过渡态理论 64
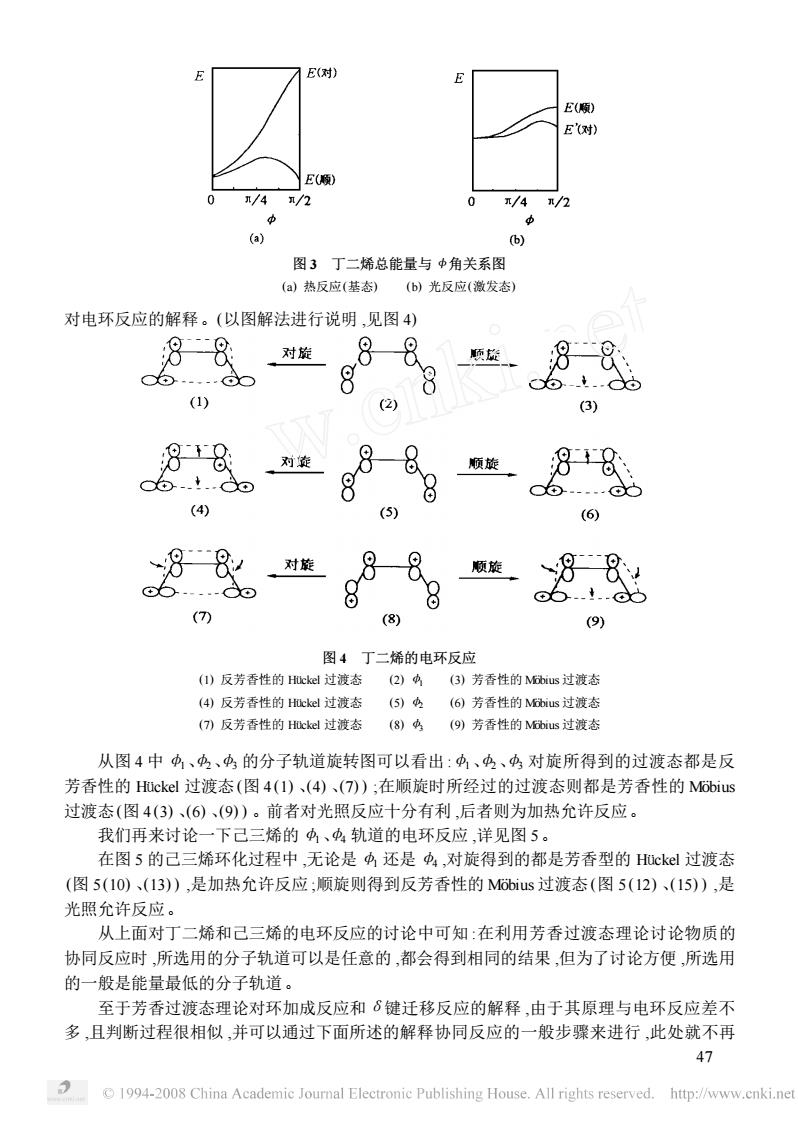
n/4/2 0 /4/2 a 6) 图3丁二烯总能量与中角关系图 (a)热反应(基态)(b)光反应(激发态) 对电环反应的解释。(以图解法进行说明,见图4) 88对881颗 8 8 6t.. (1) 2) 88对 8-8。顺旋 88 8 .... (4) (5) (6) 8-8 顺旋。 88 8 o..!..d (9) 图4丁二烯的电环反应 ()反芳香性的Hckd过渡态(2)A(B)芳香性的Mus过渡态 (4)反芳香性的Hckd过渡态 (6)芳香性的s过湾态 ()反芳香性的cd过渡态 ()今(9)芳香性的Mus过渡态 从图4中、、的分子轨道旋转图可以看出:、、对旋所得到的过渡态都是反 芳香性的HOckel过渡态(图4(1)、(4)、(7)):在顺旋时所经过的过渡态则都是芳香性的Mobius 过渡态(图4(3)、(6)、(9)。前者对光照反应十分有利,后者则为加热允许反应。 我门再来过论一下已三稀的功、功轨销的申环反应详见图5。 在图5的己三烯环化过程中,无论是4还是中,对旋得到的都是芳香型的Huckel过渡态 (图5(10)、(13),是加热允许反应;顺旋则得到反芳香性的M66ius过渡态(图5(12)、(15),是 光照允许反应。 从上面对丁二烯和己三烯的电环反应的讨论中可知:在利用芳香过渡态理论讨论物质的 协同反应时,所选用的分子轨道可以是任意的,都会得到相同的结果,但为了讨论方便,所选用 的一般是能量最低的分子轨道。 至于若香时度态理论对环加成反应和6建千移反应的解释由干其原理与申环反应差不 多,且判断过程很相似,并可以通过下面所述的解释协同反应的一般步骤来进行,此处就不再 47 194-2008 China Academie Joumal Electronie Publishing House.All rights reserved.http://www.enki.net
图 3 丁二烯总能量与 <角关系图 (a) 热反应(基态) (b) 光反应(激发态) 对电环反应的解释。(以图解法进行说明 ,见图 4) 图 4 丁二烯的电环反应 (1) 反芳香性的 Hückel 过渡态 (2) φ1 (3) 芳香性的 MÊbius 过渡态 (4) 反芳香性的 Hückel 过渡态 (5) φ2 (6) 芳香性的 MÊbius 过渡态 (7) 反芳香性的 Hückel 过渡态 (8) φ3 (9) 芳香性的 MÊbius 过渡态 从图 4 中φ1、φ2、φ3 的分子轨道旋转图可以看出 :φ1、φ2、φ3 对旋所得到的过渡态都是反 芳香性的 Hückel 过渡态(图 4 (1) 、(4) 、(7) ) ;在顺旋时所经过的过渡态则都是芳香性的 MÊbius 过渡态(图 4 (3) 、(6) 、(9) ) 。前者对光照反应十分有利 ,后者则为加热允许反应。 我们再来讨论一下己三烯的φ1、φ4 轨道的电环反应 ,详见图 5。 在图 5 的己三烯环化过程中 ,无论是φ1 还是φ4 ,对旋得到的都是芳香型的 Hückel 过渡态 (图 5 (10) 、(13) ) ,是加热允许反应 ;顺旋则得到反芳香性的 MÊbius 过渡态(图 5 (12) 、(15) ) ,是 光照允许反应。 从上面对丁二烯和己三烯的电环反应的讨论中可知 :在利用芳香过渡态理论讨论物质的 协同反应时 ,所选用的分子轨道可以是任意的 ,都会得到相同的结果 ,但为了讨论方便 ,所选用 的一般是能量最低的分子轨道。 至于芳香过渡态理论对环加成反应和δ键迁移反应的解释 ,由于其原理与电环反应差不 多 ,且判断过程很相似 ,并可以通过下面所述的解释协同反应的一般步骤来进行 ,此处就不再 74

88 对旋 顺旋 8 oo6 (10) (11) (12) Q 对酸 顺旋 88 3 (14) (15) 图5己三烯的电环反应 (I0)芳香性的Hkel过液态 (I)4(2)反芳香性的Ms过渡态 (13)芳香性的Hk如过渡态(14)A(15)反芳香性的Mus过渡态 过多地叙述。通过上面对电环反应的讨论我们可以得出解释协同反应的一般步骤如下 ①画出重叠的一和P轨道的系列的过渡态,放入“+”和“。”,并使参与轨道中的符号改 变减至最少。②计算在环排列中的符号改变数目和所包含的电子数目。③以符号的改变数 决定过渡态的Hucke!型或Mbis型,并以它的电子数目来决定它是否具有芳香性。④应用 Dewar-方nmerman规则对其进行判断,即可得出结论。 从上面的讨论中可以看出:芳香过渡态理论用于说明协同反应是简捷方便的,并且在使用 此理论的过程中并不涉及分子轨道的对称性,因此适用范围比能级相关理论要广。笔者认为 芳香过渡态理论是一种易被初学者接受的理论,它的重要性不应当在有机化学中受到忽视。 参考文献 TL,S0TRC.有机反应与轨道对称性.张水敏译上海:上海科学技术出版社,198 王玉珠有机化学现代电子理论辽宁:辽宁教育出版社,198 刘宗明.分子轨道对称守恒原理及其在有机化学中的应用.北京:高等教育出版社,1983 小资料· 1999年原子量新标准 PAC原子量与同位素丰度委员会在1999年8月8~10日柏林会议上,决定采用下列原子量的新标准 (括号内的数指末位数的不确定度)。表中储和饵的新标准值系北京大学张青莲教授等的测定结果。 元素符号新标准值 旧值 元素符号新标准值 旧值 N 14.0067(2) 14.00674(7) Xe 131.293(6) 131.29(2) 32.06551 32.066(6) 167.259(3) 167.26(3) 35.453(2) 35.4527(9 11 238.02891(3) 238.0289(1) 2.64 2.612) [童卫粟] 48 1994-2008 China Academic Joumal Electronic Publishing House.All rights reserved. http://www.cnki.ne
图 5 己三烯的电环反应 (10) 芳香性的 Hückel 过渡态 (11) φ1 (12) 反芳香性的 MÊbius 过渡态 (13) 芳香性的 Hückel 过渡态 (14) φ4 (15) 反芳香性的 MÊbius 过渡态 过多地叙述。通过上面对电环反应的讨论 ,我们可以得出解释协同反应的一般步骤如下 : ①画出重叠的 s2和 p2轨道的系列的过渡态 ,放入“+ ”和“- ”,并使参与轨道中的符号改 变减至最少。②计算在环排列中的符号改变数目和所包含的电子数目。③以符号的改变数 决定过渡态的 Hückel 型或 MÊbius 型 ,并以它的电子数目来决定它是否具有芳香性。④应用 Dewar2Zimmerman 规则对其进行判断 ,即可得出结论。 从上面的讨论中可以看出 :芳香过渡态理论用于说明协同反应是简捷方便的 ,并且在使用 此理论的过程中并不涉及分子轨道的对称性 ,因此适用范围比能级相关理论要广。笔者认为 芳香过渡态理论是一种易被初学者接受的理论 ,它的重要性不应当在有机化学中受到忽视。 参 考 文 献 1 Gilchrist T L , Storr R C. 有机反应与轨道对称性. 张永敏译. 上海 :上海科学技术出版社 , 1981 2 王玉珠. 有机化学现代电子理论. 辽宁 :辽宁教育出版社 , 1986 3 刘宗明. 分子轨道对称守恒原理及其在有机化学中的应用. 北京 :高等教育出版社 , 1983 ·小资料· 1999 年原子量新标准 IUPAC原子量与同位素丰度委员会在 1999 年 8 月 8~10 日柏林会议上 ,决定采用下列原子量的新标准 (括号内的数指末位数的不确定度) 。表中锗和铒的新标准值系北京大学张青莲教授等的测定结果。 元素 符号 新标准值 旧 值 元素 符号 新标准值 旧 值 氮 N 14. 0067(2) 14. 00674(7) 氙 Xe 131. 293(6) 131. 29(2) 硫 S 32. 065(5) 32. 066(6) 铒 Er 167. 259(3) 167. 26(3) 氯 Cl 35. 453(2) 35. 4527(9) 铀 U 238. 02891(3) 238. 0289(1) 锗 Ge 72. 64(1) 72. 61(2) [童卫粟] 84