
仪器分析(含实验) 《仪器分析》课程 第十章 原子吸收光增法 Chapter Ten Atomic Absorption Spectrum For Short:AAS
《仪器分析》课程 仪器分析(含实验) 第十章 Chapter Ten Atomic Absorption Spectrum For Short:AAS 原子吸收光谱法

§10.1概述 1.原子吸收光谱 米溶液中的金属离子化合物在高温下能够解离成原子蒸气, 两种形态间存在定量关系。 米当光源发射出的特征波长光辐射通过原子蒸气时,原子中 的外层电子吸收能量,特征谱线的光强度减弱。 米光强度的变化符合朗伯比耳定律,进行定量分析。 它是基于物质所产生的原子蒸气对特征谱线的吸收 作用来进行定量分析的一种方法。 冬原子与分子一样,吸收特定能量后,产生基态→激发态跃迁 ;产生原子吸收光谱,即共振吸收。 冬原子由基态→第一激发态的跃迁,最易发生。 冬每种原子的核外电子能级分布不同,当产生由基态→第一 激发态的跃迁时,吸收特定频率的辐射能量。 冬原子吸收光谱是线状光谱
§ 10.1 概述 它是基于物质所产生的原子蒸气对特征谱线的吸收 作用来进行定量分析的一种方法。 1. 原子吸收光谱 溶液中的金属离子化合物在高温下能够解离成原子蒸气, 两种形态间存在定量关系。 当光源发射出的特征波长光辐射通过原子蒸气时,原子中 的外层电子吸收能量,特征谱线的光强度减弱。 光强度的变化符合朗伯-比耳定律,进行定量分析。 ❖原子与分子一样,吸收特定能量后,产生基态→激发态跃迁 ;产生原子吸收光谱,即共振吸收。 ❖原子由基态→第一激发态的跃迁,最易发生。 ❖每种原子的核外电子能级分布不同,当产生由基态→第一 激发态的跃迁时,吸收特定频率的辐射能量。 ❖原子吸收光谱是线状光谱
原子吸收现象早在上世纪已被人们所知,但一直未能应用于 元素的实际分析。 1955年,澳大利亚物理学家沃尔森(Wash)采用特殊装置,成 功地建立了原子吸收分析方法,发表了经典论文:“原子吸收分 光光度法在分析化学中的应用”。 2.原子吸收光谱与原子发射光谱的关系 子 共振线与吸收线原子发射光谱称共振发射线 共 电,热能 基态 第一激发态 →基态 荧 h h 基态 第一激发态 原子吸收光谱称为 共振吸收线 3.基态原子数N,与各激发态原子数N的关系 在高温下,处于热力学平衡状态时,单位体积的基态原子数 N与激发态原子数N之间遵守Boltzmann分布定律: N=No g:/go e-EVKT
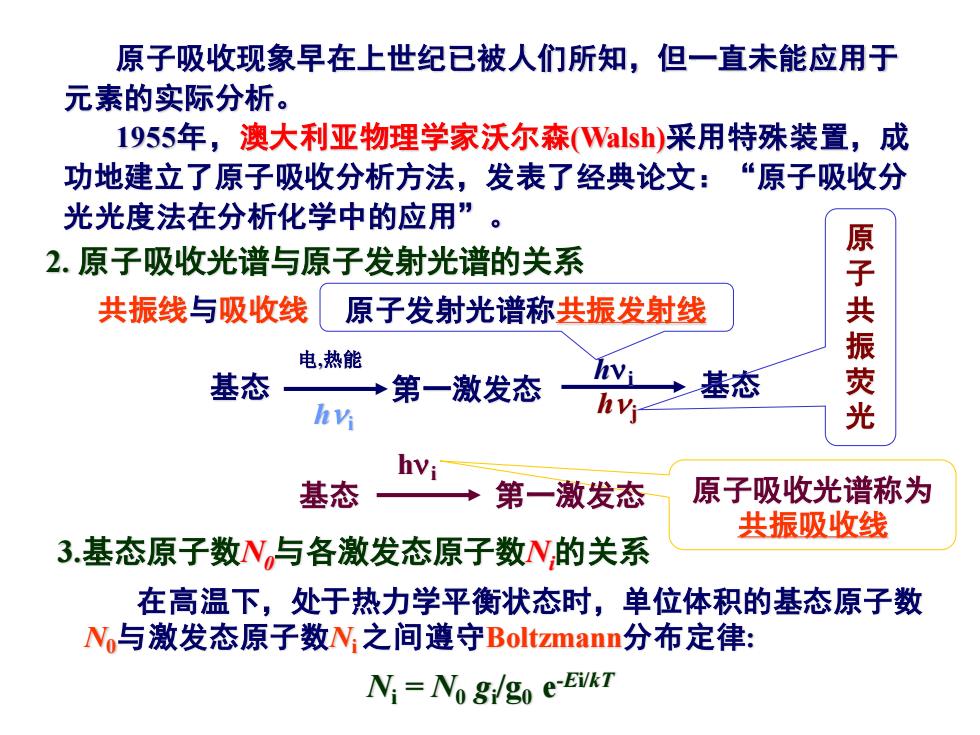
2. 原子吸收光谱与原子发射光谱的关系 共振线与吸收线 基态 第一激发态 基态 电,热能 hi h i h j 原子发射光谱称共振发射线 原 子 共 振 荧 光 原子吸收光谱称为 共振吸收线 基态 第一激发态 hi 3.基态原子数N0与各激发态原子数Ni的关系 Ni = N0 gi /g0 e -Ei/kT 在高温下,处于热力学平衡状态时,单位体积的基态原子数 N0与激发态原子数Ni之间遵守Boltzmann分布定律: 原子吸收现象早在上世纪已被人们所知,但一直未能应用于 元素的实际分析。 1955年,澳大利亚物理学家沃尔森(Walsh)采用特殊装置,成 功地建立了原子吸收分析方法,发表了经典论文:“原子吸收分 光光度法在分析化学中的应用
§10.2原子光谱线的轮廓 Kv 原子吸收光谱线轮廓图 一.原子光谱线(吸收线)的宽度 Ko 2最大吸收系数 3.谱线半宽度(102A) K/2 1.谱线中心频率 : 二 原子光谱线变宽的因素 E 器 收 射 hy h 1.吸收线能量与波长关系 Eo Eo hc/AE 不产生能级变宽 产生能级变宽
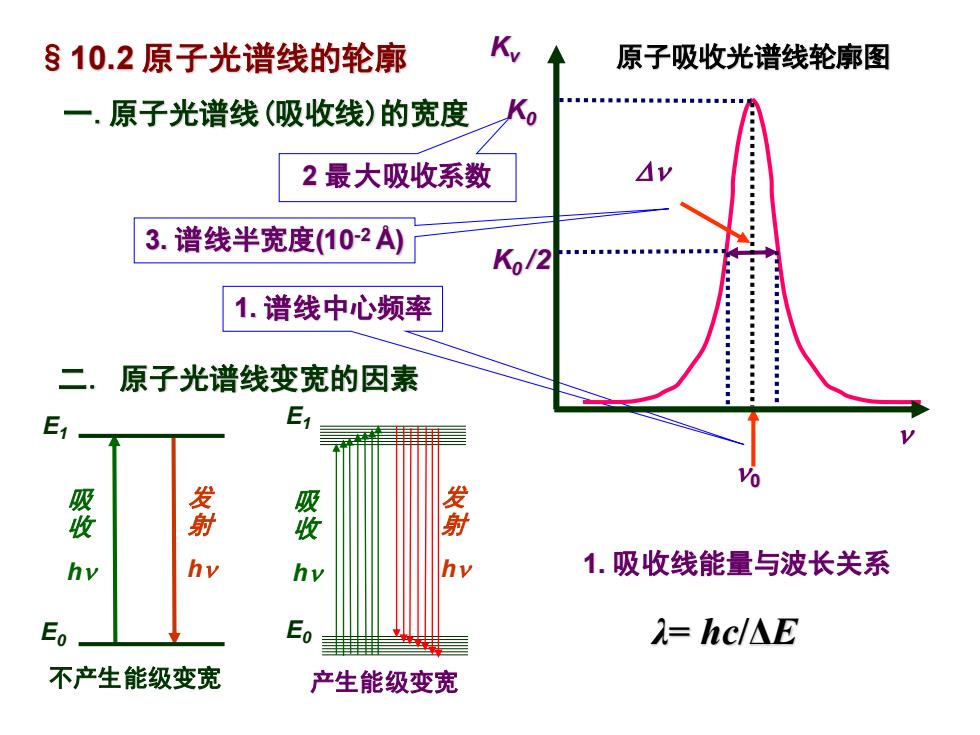
§10.2 原子光谱线的轮廓 一.原子光谱线(吸收线)的宽度 原子吸收光谱线轮廓图 3. 谱线半宽度(10-2 Å) 1. 谱线中心频率 2 最大吸收系数 0 Kv K0 K0 /2 二. 原子光谱线变宽的因素 1. 吸收线能量与波长关系 λ= hc/ΔE 吸 收 h 发 射 h E0 E1 E0 E1 吸 收 h 发 射 h 不产生能级变宽 产生能级变宽

2.自然宽度△ 与原子外层电子发生能级间跃迁时激发态原子的寿命有关,是 客观存在。一般情况下约相当于10A,通常可以忽略。 3.多普勤宽度AVo(Doppler Broadening) 这是由原子在空间作无规热运动所引致的。故又称热变宽。 T 式中:M-原子量; △m=7.16×107vo, T-绝对温度; M Vo-谱线中心频率 即使在较低的温度,也比自然宽度△人来得严重,是谱线变 宽的主要因素.一般情况:△VD=102A. 4.压力变宽(碰撞变宽) 原子与等离子体中的其他粒子(原子、离子、电子)相互碰撞 而使谱线变宽,等离子体蒸气压力愈大,谱线愈宽。 同种粒子碰撞称赫尔兹马克(Holtzmank)变宽. 冬异种粒子碰撞称罗论兹(Lorent忆)变宽。 压力变宽(碰撞变宽)为102A,也是谱线变宽的主要因素
M T νD ν 0 7 = 7.16×10- 式中:M - 原子量; T - 绝对温度; 0 - 谱线中心频率 即使在较低的温度,也比自然宽度Δ N来得严重,是谱线变 宽的主要因素.一般情况: ΔD=10-2Å . 4. 压力变宽(碰撞变宽) 原子与等离子体中的其他粒子(原子、离子、电子)相互碰撞 而使谱线变宽,等离子体蒸气压力愈大,谱线愈宽。 ❖ 同种粒子碰撞——称赫尔兹马克(Holtzmank)变宽. ❖ 异种粒子碰撞——称罗论兹(Lorentz)变宽。 压力变宽(碰撞变宽)为10-2Å,也是谱线变宽的主要因素. 3. 多普勤宽度Δ D (Doppler Broadening) 这是由原子在空间作无规热运动所引致的。故又称热变宽。 2. 自然宽度ΔN 与原子外层电子发生能级间跃迁时激发态原子的寿命有关,是 客观存在。一般情况下约相当于10-4Å,通常可以忽略
5.自吸变宽 当基态、气态原子密度较大时产生。 图2一3增线的自吸 6.场致变宽 1一无自吸;2一自吸:3一自蚀 斯塔克变宽(Stark Broadening):由于外部的电场或等离子体中 离子、电子所形成的电场引起。 齐曼变宽(Zeeman Broadening):由于外部的磁场影响,导致谱线 的分裂,在单色器分辨率无法 分辨时,也产生谱线变宽。 在1000~3000K、0.101MPa状态,多普勤宽度△yo和压力变 宽(碰撞变宽)是谱线变宽的主要因素
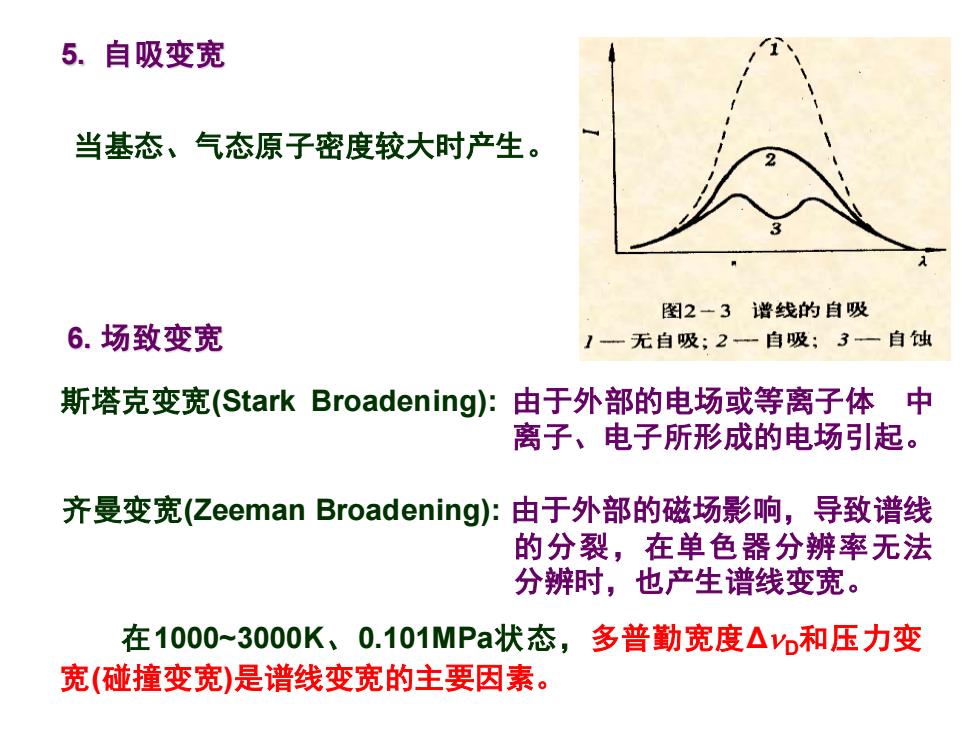
6. 场致变宽 斯塔克变宽(Stark Broadening): 由于外部的电场或等离子体 中 离子、电子所形成的电场引起。 在1000~3000K、0.101MPa状态,多普勤宽度Δ D和压力变 宽(碰撞变宽)是谱线变宽的主要因素。 齐曼变宽(Zeeman Broadening): 由于外部的磁场影响,导致谱线 的分裂,在单色器分辨率无法 分辨时,也产生谱线变宽。 5. 自吸变宽 当基态、气态原子密度较大时产生
§10.3原子吸收光谱的测量 一.积分吸收 Ko 积 πe2 ∫K,dw=πefN 分 mc K/2 公 f-振子强度 式 为电子电荷 N-单位积内的自由原子数 m-电子的质量 二.积分吸收的限制 式中: Vo 1.平面衍射光栅分辨率R 入是相邻两谱线的平均波长; 41是相邻两谱线的波长差; 元 R= =kN k是光谱的级次; △2 N是光栅的刻线数。 在5000A的波长,要积分半宽度为0.01A的谱线,至少要取10点,每点 为0.001A。根据分辨率公式,可以计算光栅所需的分辨率R和光栅常数d。 R= 5000 ×106 =1×105(条/mm) 目前,光栅常数d 0.001 =5×106d= 50mm 无法达到此要求
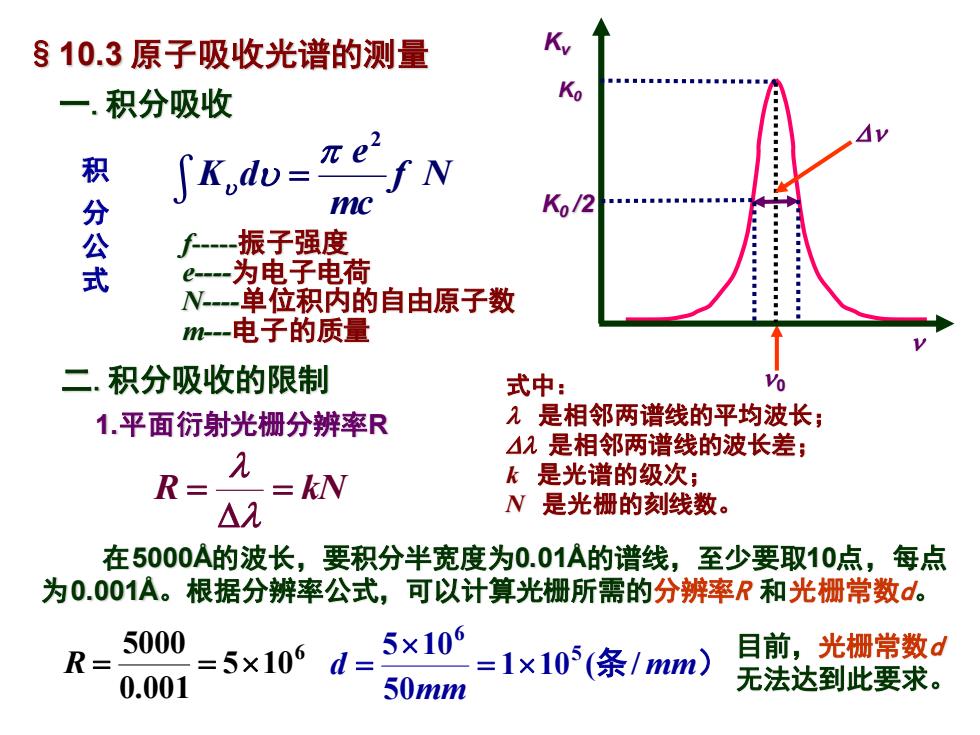
一.积分吸收 f N mc e ∫K d 2 = f-振子强度 e-为电子电荷 N-单位积内的自由原子数 m-电子的质量 §10.3 原子吸收光谱的测量 积 分 公 式 0 Kv K0 K0 /2 1.平面衍射光栅分辨率R R = kN = 式中: 是相邻两谱线的平均波长; 是相邻两谱线的波长差; k 是光谱的级次; N 是光栅的刻线数。 二.积分吸收的限制 6 5 10 0.001 5000 R = = 在5000Å的波长,要积分半宽度为0.01Å的谱线,至少要取10点,每点 为0.001Å。根据分辨率公式,可以计算光栅所需的分辨率R 和光栅常数d。 条 mm) mm d 1 10 ( / 50 5 10 5 6 = = 目前,光栅常数d 无法达到此要求

2.单色器的光谱通带 光谱通带W:WDxS 式中:S-缝宽度(mm) D-倒线色散率(nm/mm) 当光谱通带:1 =0.001A.S=0.007(mm) 倒线色散率:D=S/仁0.001×10-6nm/0.007(mm) =1.4×10-7nm/mm) 目前,倒线色散率D也无法达到此要求。 3.检测器的灵敏度 即使光栅常数d、光谱通带W,倒线色散率D都达到此要求,还要 考虑到检测器的灵敏度;在以上条件下检测器的灵敏度也无法达到要求。 综合以上讨论: 如果我们测量KdU,就可求出原子浓度N,但是谱线宽度为102A左 右。需要用高分辨率的分光仪器,高灵敏度的检测器这是目前难以达到的。 这就是早在100多年前就已发现原子吸收的现象,但一直难以使用于分析 科学的原因
2.单色器的光谱通带 光谱通带W : W=DS 当光谱通带: W=0.001Å ,S=0.007(mm) 式中: S- 缝宽度(mm) D-倒线色散率(nm/mm) 倒线色散率: D = S / W= 0.001 10-6nm / 0.007(mm) = 1.4 10-7 (nm/mm) 目前,倒线色散率D也无法达到此要求。 3.检测器的灵敏度 即使光栅常数d 、光谱通带W、倒线色散率D都达到此要求,还要 考虑到检测器的灵敏度;在以上条件下检测器的灵敏度也无法达到要求。 综合以上讨论: 如果我们测量∫Kvdυ , 就可求出原子浓度N,但是谱线宽度为10-2Å左 右。需要用高分辨率的分光仪器,高灵敏度的检测器这是目前难以达到的。 这就是早在100多年前就已发现原子吸收的现象,但一直难以使用于分析 科学的原因

三.峰值吸收 1.积分吸收与峰值吸收的关系:1955年澳大利亚学者沃尔森Wlsh) 提出,在温度不太高的稳定火焰条件下,峰值吸收系数与火焰 中被测元素的原子浓度也正比。 积分吸收与火焰中基态 SKvdv=πe2 N●f 原子数的关系为: (1) mc 尚级者费晒子的热运动时,K,=K0×exp-2业-四m2} 吸收系数的关系为: (2) △b 把式(2)积分后,得到: 1πK△VD Kvdw=2V1n2 (3) 0 合并式(1)与(3) r e2 1 整理后,得到: N●f= -KoAVD me In 2 ze2 2 整理后,得到: K= ●N●f (4 △Vp a mc 由式(4)可以得出峰值吸收系数K,与自由原子数W成正比
ln 2] } (2) 2( ) ×exp{ [ 2 0 0 D K K − = − (3) 2 ln 2 1 0 0 K d K D = 三.峰值吸收 (1) 2 N f mc e K d = • 积分吸收与火焰中基态 ∫ 原子数的关系为: 当仅考虑原子的热运动时, 吸收系数的关系为: 把式(2)积分后,得到: 1. 积分吸收与峰值吸收的关系: 1955年澳大利亚学者沃尔森(Walsh) 提出,在温度不太高的稳定火焰条件下,峰值吸收系数与火焰 中被测元素的原子浓度也正比。 K D N f mc e • = 0 2 2 ln 2 合并式(1)与(3) 1 整理后,得到: (4) 2 ln 2 2 0 N f mc e K D • • • = 整理后,得到: 由式(4)可以得出峰值吸收系数K0与自由原子数N成正比
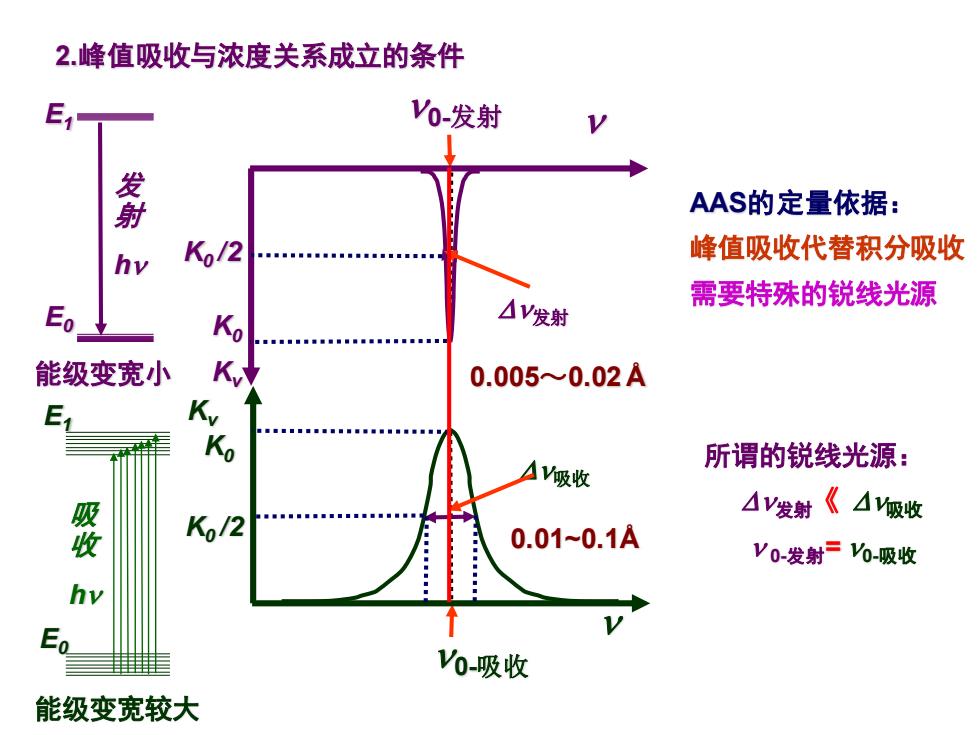
2峰值吸收与浓度关系成立的条件 E1 Vo-发射 射 AAS的定量依据: hy Ko/2 峰值吸收代替积分吸收 需要特殊的锐线光源 Eo Ko △V发射 能级变宽小 K 0.0050.02A Kv ■■■■ Ko 所谓的锐线光源: AV吸收 △V发射《△吸收 收 Ko/2 0.010.1A V0-发射=V6-吸收 Vo-吸收 能级变宽较大
2.峰值吸收与浓度关系成立的条件 发 射 h E0 E1 吸 收 h 能级变宽小 能级变宽较大 E0 E1 0-吸收 Kv K0 K0 /2 吸收 发射 0-发射 Kv K0 K0 /2 AAS的定量依据: 峰值吸收代替积分吸收 需要特殊的锐线光源 所谓的锐线光源: 发射《 吸收 0-发射= 0-吸收 0.01~0.1Å 0.005~0.02 Å