
仪器分析(含实验) 《仪器分析》课程 第十三章 红外吸收光谱法 Chapter Thirteen Infrared Absorption Spectrum For Short:IR
《仪器分析》课程 仪器分析(含实验) 第十三章 Chapter Thirteen Infrared Absorption Spectrum For Short: IR 红外吸收光谱法
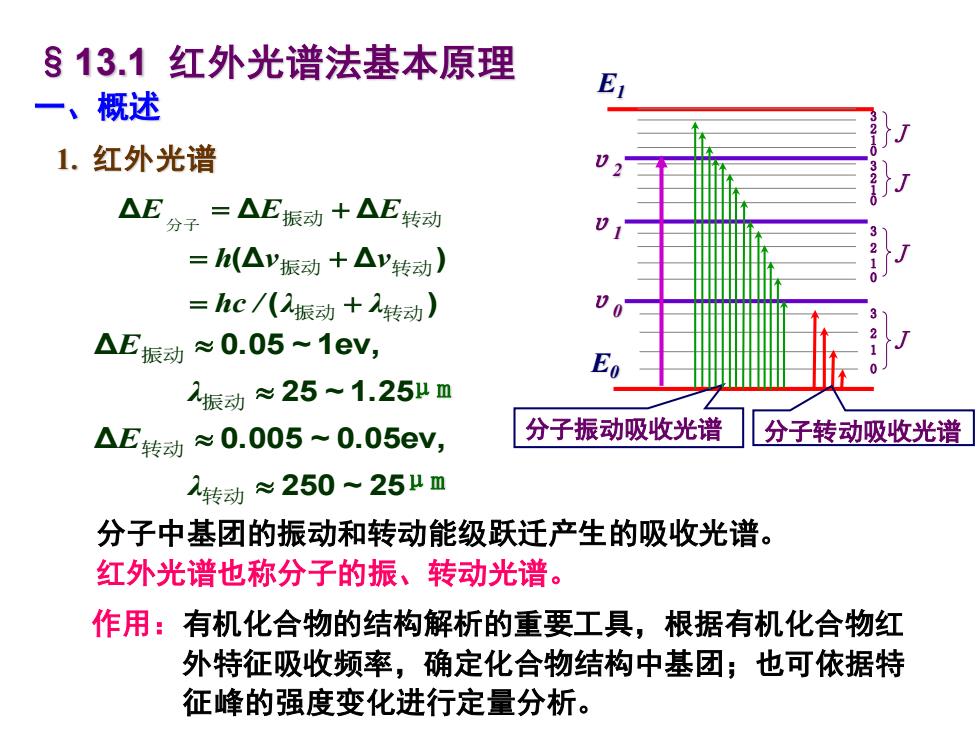
§13.1红外光谱法基本原理 一、概述 1.红外光谱 AE分子=AE振动+AE转动 =h(△V振动+△V转动) =hc/八2振动+转动) △E振动≈0.05~1eV, 振动≈25~1.25μm △E转动≈0.005~0.05eV, 分子振动吸收光谱 分子转动吸收光谱 转动≈250~25μm 分子中基团的振动和转动能级跃迁产生的吸收光谱。 红外光谱也称分子的振、转动光谱。 作用:有机化合物的结构解析的重要工具,根据有机化合物红 外特征吸收频率,确定化合物结构中基团;也可依据特 征峰的强度变化进行定量分析
一、概述 分子中基团的振动和转动能级跃迁产生的吸收光谱。 红外光谱也称分子的振、转动光谱。 1. 红外光谱 §13.1 红外光谱法基本原理 E1 E0 υ0 υ1 υ2 1 J 0 2 3 J 0 2 3 1 J 0 2 3 1 J 0 2 3 1 分子振动吸收光谱 分子转动吸收光谱 ( ) (Δ Δ ) Δ Δ Δ 振动 转动 振动 转动 分子 振动 转动 hc / λ λ h ν ν E E E = + = + = + 250 ~ 25 Δ 0.005 ~ 0.05ev, 25 ~ 1.25 Δ 0.05 ~ 1ev, 转动 转动 振动 振动 λ E λ E μm μm 作用:有机化合物的结构解析的重要工具,根据有机化合物红 外特征吸收频率,确定化合物结构中基团;也可依据特 征峰的强度变化进行定量分析
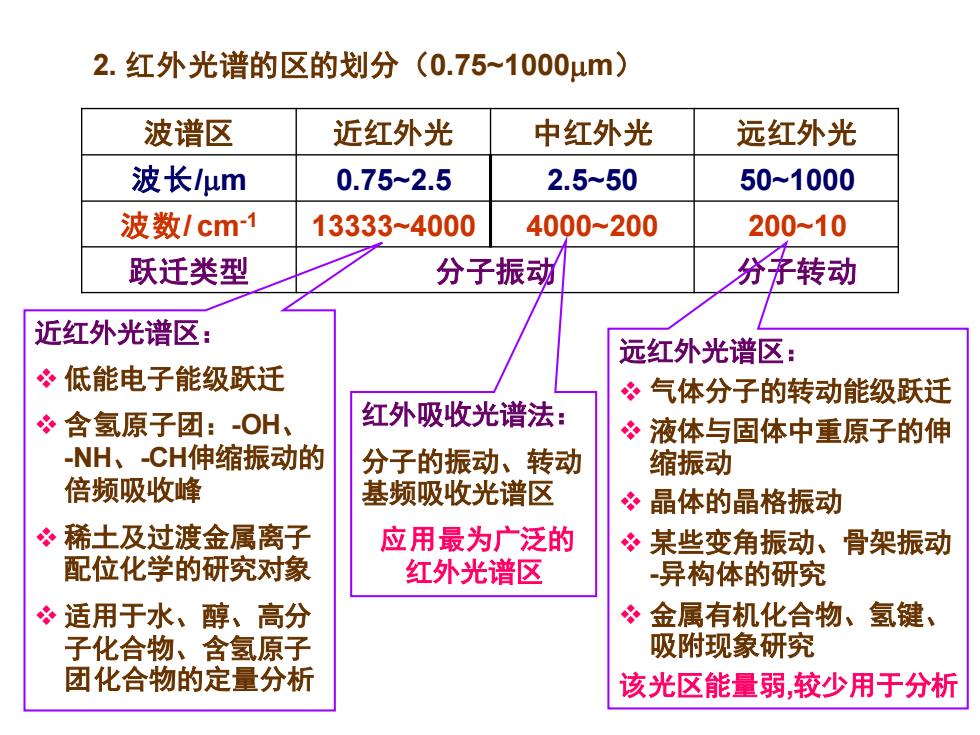
2.红外光谱的区的划分(0.75~1000μm) 波谱区 近红外光 中红外光 远红外光 波长μm 0.75-2.5 2.5-50 50~1000 波数/cm1 13333-4000 4000-200 200~10 跃迁类型 分子振动 分子转动 近红外光谱区: 远红外光谱区: 低能电子能级跃迁 冬气体分子的转动能级跃迁 含氢原子团:-OH、 红外吸收光谱法: 冬液体与固体中重原子的伸 NH、-CH伸缩振动的 分子的振动、转动 缩振动 倍频吸收峰 基频吸收光谱区 ?晶体的晶格振动 冬稀土及过渡金属离子 应用最为广泛的 冬某些变角振动、骨架振动 配位化学的研究对像 红外光谱区 -异构体的研究 ?适用于水、醇、高分 冬金属有机化合物、氢键、 子化合物、含氢原子 吸附现象研究 团化合物的定量分析 该光区能量弱,较少用于分析
波谱区 近红外光 中红外光 远红外光 波长/m 0.75~2.5 2.5~50 50~1000 波数/ cm-1 13333~4000 4000~200 200~10 跃迁类型 分子振动 分子转动 近红外光谱区: ❖ 低能电子能级跃迁 ❖ 含氢原子团:-OH、 -NH、-CH伸缩振动的 倍频吸收峰 ❖ 稀土及过渡金属离子 配位化学的研究对象 ❖ 适用于水、醇、高分 子化合物、含氢原子 团化合物的定量分析 红外吸收光谱法: 分子的振动、转动 基频吸收光谱区 应用最为广泛的 红外光谱区 远红外光谱区: ❖ 气体分子的转动能级跃迁 ❖ 液体与固体中重原子的伸 缩振动 ❖ 晶体的晶格振动 ❖ 某些变角振动、骨架振动 -异构体的研究 ❖ 金属有机化合物、氢键、 吸附现象研究 该光区能量弱,较少用于分析 2. 红外光谱的区的划分(0.75~1000m)
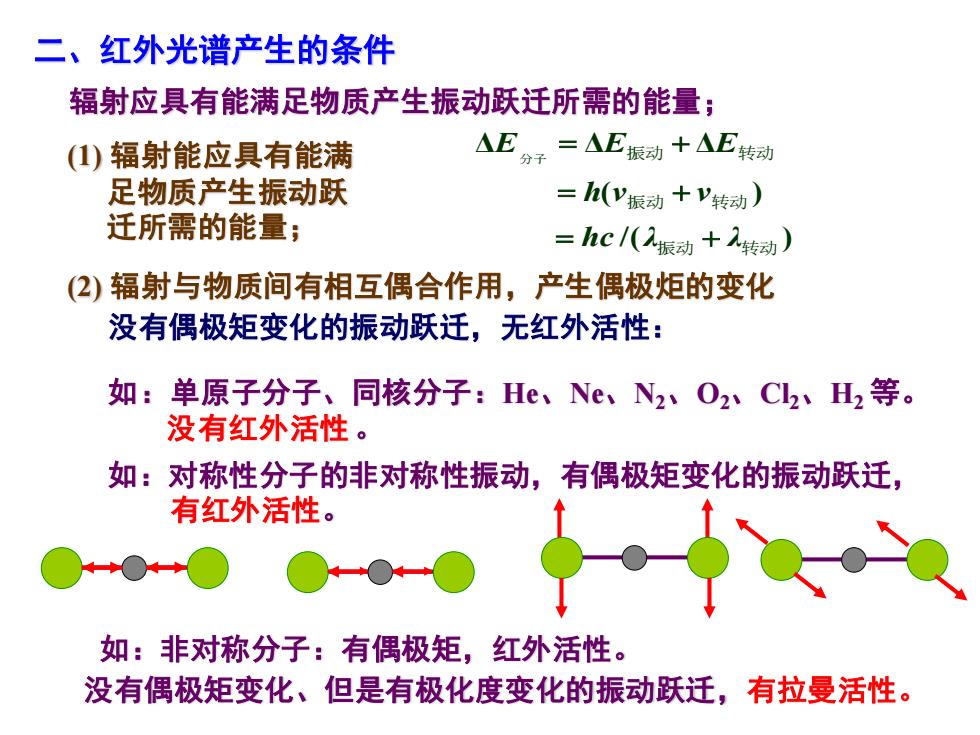
二、红外光谱产生的条件 辐射应具有能满足物质产生振动跃迁所需的能量; ()辐射能应具有能满 △E分子=△E振动十AE转动 足物质产生振动跃 =h(y振动+V转动) 迁所需的能量; =hc/(2振动+人转动) (2)辐射与物质间有相互偶合作用,产生偶极炬的变化 没有偶极矩变化的振动跃迁,无红外活性: 如:单原子分子、同核分子:He、Ne、N2、O2C2、H2等。 没有红外活性。 如:对称性分子的非对称性振动,有偶极矩变化的振动跃迁, 有红外活性。 如:非对称分子:有偶极矩,红外活性。 没有偶极矩变化、但是有极化度变化的振动跃迁,有拉曼活性
二、红外光谱产生的条件 (2) 辐射与物质间有相互偶合作用,产生偶极炬的变化 (1) 辐射能应具有能满 足物质产生振动跃 迁所需的能量; /( ) ( ) Δ Δ Δ 振动 转动 振动 转动 分子 振动 转动 hc λ λ h ν ν E E E = + = + = + 辐射应具有能满足物质产生振动跃迁所需的能量; 没有偶极矩变化的振动跃迁,无红外活性: 如:单原子分子、同核分子:He、Ne、N2、O2、Cl2、H2 等。 没有红外活性 。 如:对称性分子的非对称性振动,有偶极矩变化的振动跃迁, 有红外活性。 如:非对称分子:有偶极矩,红外活性。 没有偶极矩变化、但是有极化度变化的振动跃迁,有拉曼活性

三、双原子分子振动方程式 1.双原子分子的简谐振动及其频率 分子的振动能级(量子化): E振动=(41/2)hy v:化学键的振动频率; V振动量子数(=0、1、2.),当=0时,E0,称为零点能。 根据经典力学的虎克定律: h K △E振动= 2πV4 v(cm)= k-化学键的力常数(达因),与键能和键长有关; -双原子的折合质量: u=mm2/(m1+m2) (cm')=1=1k λ2πCV4 =1307 k-化学键的力常数(NWcm),与键能和键长有关; 4-双原子的折合原子量:4=M,M,(M+M2)
三、双原子分子振动方程式 1.双原子分子的简谐振动及其频率 分子的振动能级(量子化): E振动=(V+1/2)hν ν:化学键的振动频率; V: 振动量子数(V=0、1、2.),当V=0时,E≠0,称为零点能。 根据经典力学的虎克定律: κ 2 h E振 动 = k C v 2 1 (cm ) -1 ~ = k-化学键的力常数(达因) ,与键能和键长有关; μ-双原子的折合质量: μ =m1m2 /(m1+m2 ) k-化学键的力常数(N/cm) ,与键能和键长有关; μ-双原子的折合原子量: μ =M1M2 /(M1+M2 )。 π k k C v 1307 2 1 1 (cm ) -1 = = = − λ μ μ
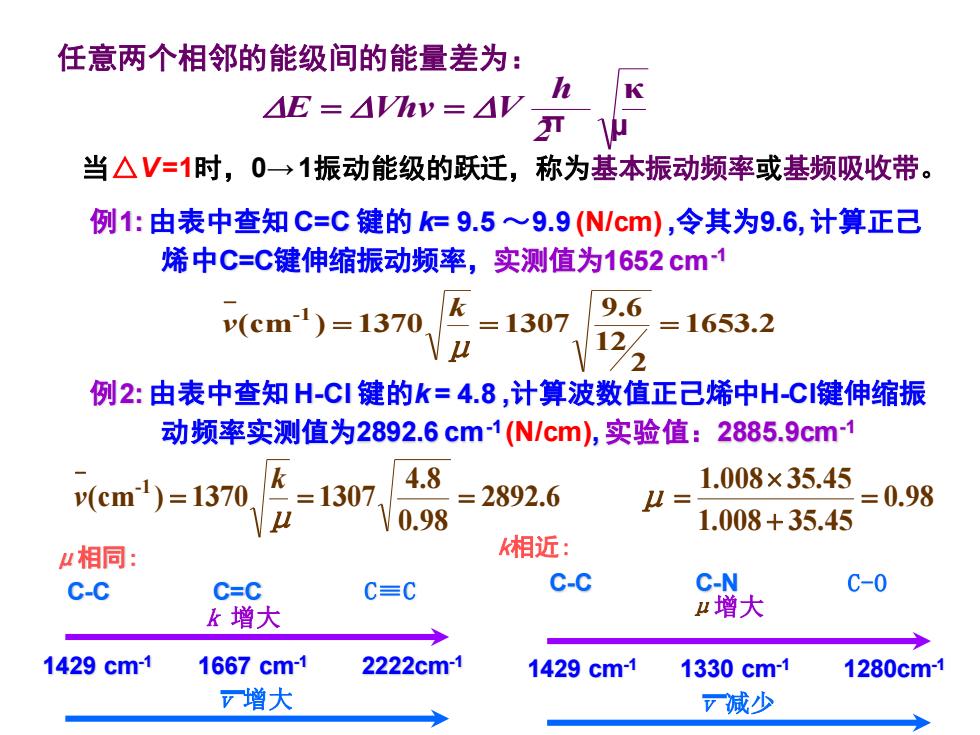
任意两个相邻的能级间的能量差为: h AE=AVhv=AV- 当△V=1时,0→1振动能级的跃迁,称为基本振动频率或基频吸收带。 例1:由表中查知C=C键的k=9.5~9.9(N/cm),令其为9.6,计算正己 烯中C=C键伸缩振动频率,实测值为1652cm-1 v(cml)=1370 /k=1307 9.6 12 =1653.2 例2:由表中查知H-C1键的k=4.8,计算波数值正己烯中H-C键伸缩振 动频率实测值为2892.6cm-1(N/cm),实验值:2885.9cm-1 4.8 1.008×35.45 v(cm)=1370 =1307 =2892.6 =0.98 0.98 1.008+35.45 4相同: 相近: C-C C=C C=C C-C C-N C-0 k增大 增大 1429cm-1 1667cm-1 2222cm-1 1429cm-1 1330cm-1 1280cm-1 增大 减少
μ增大 v 减少 k 增大 v 增大 例1: 由表中查知 C=C 键的 k= 9.5 ~9.9 (N/cm) ,令其为9.6, 计算正己 烯中C=C键伸缩振动频率,实测值为1652 cm-1 1653.2 2 12 9.6 (cm ) 1370 1307 -1 = = = − k v μ 例2: 由表中查知 H-Cl 键的k = 4.8 ,计算波数值正己烯中H-Cl键伸缩振 动频率实测值为2892.6 cm-1 (N/cm), 实验值:2885.9cm-1 0.98 1.008 35.45 1.008 35.45 2892.6 0.98 4.8 (cm ) 1370 1307 -1 = + = = = = − k v μ μ C-C C=C C≡C μ相同: 1429 cm-1 1667 cm-1 2222cm-1 C-C C-N C-O 1429 cm-1 1330 cm-1 1280cm-1 k相近: 任意两个相邻的能级间的能量差为: κ 2 h E = Vhv = V π μ 当△V=1时,0→ 1振动能级的跃迁,称为基本振动频率或基频吸收带
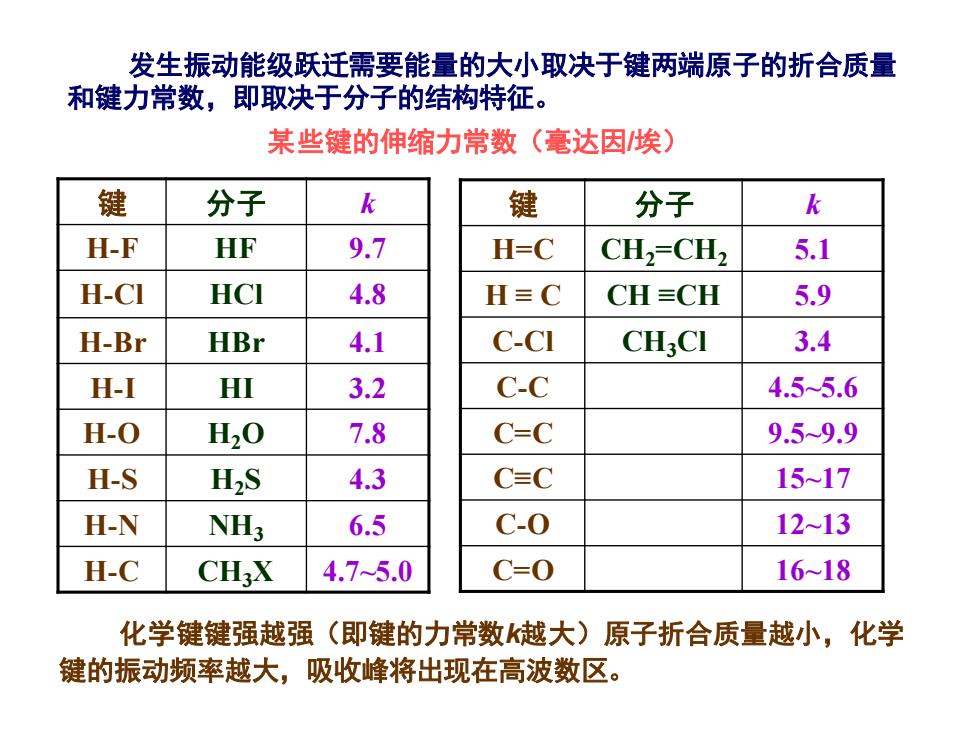
发生振动能级跃迁需要能量的大小取决于键两端原子的折合质量 和键力常数,即取决于分子的结构特征。 某些键的伸缩力常数(毫达因埃) 键 分子 键 分子 k H-F HF 9.7 H=C CH,=CH2 5.1 H-CI HCI 4.8 H≡C CH≡CH 5.9 H-Br HBr 4.1 C-CI CH;CI 3.4 H-I HI 3.2 C-C 4.5-5.6 H-O H20 7.8 C=C 9.59.9 H-S H>S 4.3 C≡C 15~17 H-N NH3 6.5 12~13 H-C CH:X 4.75.0 Y=0 16~18 化学键键强越强(即键的力常数k越大)原子折合质量越小,化学 键的振动频率越大,吸收峰将出现在高波数区
发生振动能级跃迁需要能量的大小取决于键两端原子的折合质量 和键力常数,即取决于分子的结构特征。 某些键的伸缩力常数(毫达因/埃) 键 分子 k H-F HF 9.7 H-Cl HCl 4.8 H-Br HBr 4.1 H-I HI 3.2 H-O H2O 7.8 H-S H2S 4.3 H-N NH3 6.5 H-C CH3X 4.7~5.0 化学键键强越强(即键的力常数k越大)原子折合质量越小,化学 键的振动频率越大,吸收峰将出现在高波数区。 键 分子 k H=C CH2=CH2 5.1 H ≡ C CH ≡CH 5.9 C-Cl CH3Cl 3.4 C-C 4.5~5.6 C=C 9.5~9.9 C≡C 15~17 C-O 12~13 C=O 16~18
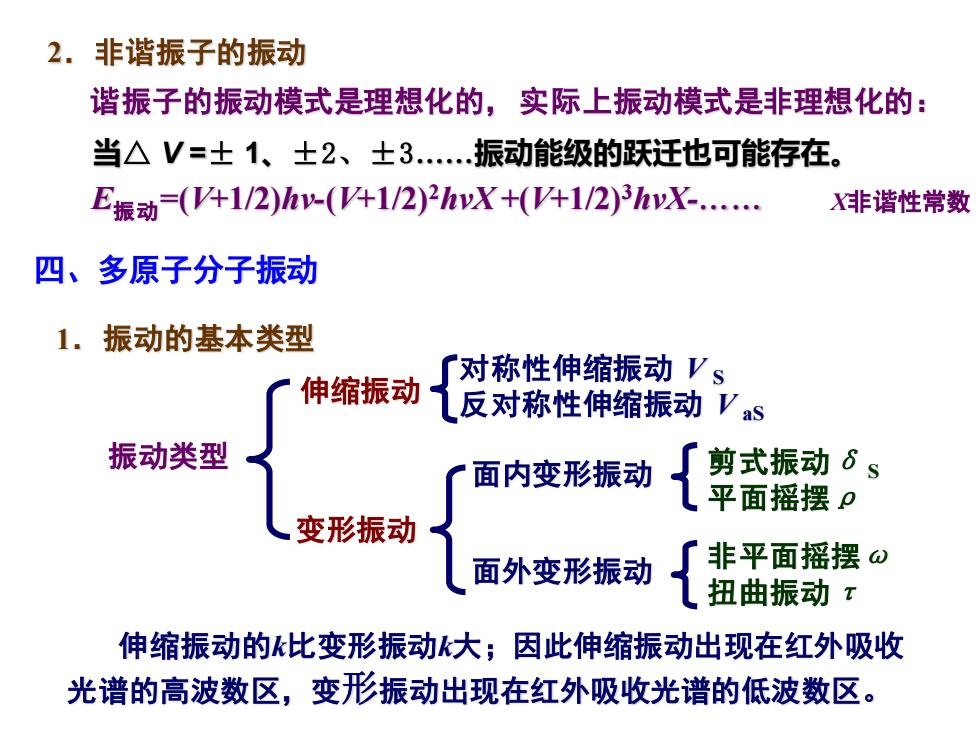
2.非谐振子的振动 谐振子的振动模式是理想化的,实际上振动模式是非理想化的: 当△V=士1、土2、士3.振动能级的跃迁也可能存在。 E振动=(41/2)h(41/2)2hX+(41/2)3hK. X非谐性常数 四、多原子分子振动 1.振动的基本类型 『对称性伸缩振动Vs 伸缩振动 反对称性伸缩振动Vs 振动类型 面内变形振动 剪式振动6s 平面摇摆p 变形振动 面外变形振动 非平面摇摆⊙ 扭曲振动T 伸缩振动的k比变形振动k大;因此伸缩振动出现在红外吸收 光谱的高波数区,变形振动出现在红外吸收光谱的低波数区
2.非谐振子的振动 谐振子的振动模式是理想化的, 实际上振动模式是非理想化的: E振动=(V+1/2)hν-(V+1/2)2hνX +(V+1/2)3hνX-. 当△ V =± 1、±2、±3.振动能级的跃迁也可能存在。 X非谐性常数 四、多原子分子振动 1.振动的基本类型 对称性伸缩振动 V S 反对称性伸缩振动 V aS 面内变形振动 面外变形振动 变形振动 振动类型 非平面摇摆ω 扭曲振动τ 剪式振动δ S 平面摇摆ρ 伸缩振动 伸缩振动的k比变形振动k大;因此伸缩振动出现在红外吸收 光谱的高波数区,变形振动出现在红外吸收光谱的低波数区
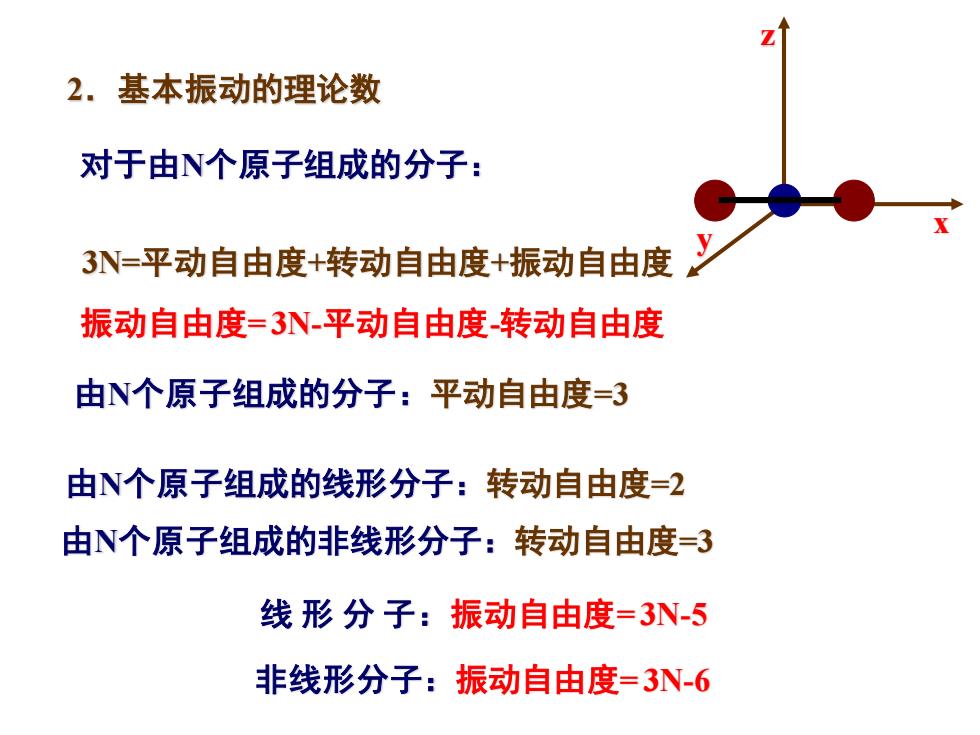
2.基本振动的理论数 对于由N个原子组成的分子: 3N=平动自由度+转动自由度+振动自由度 振动自由度=3N-平动自由度转动自由度 由N个原子组成的分子:平动自由度=3 由N个原子组成的线形分子:转动自由度=2 由N个原子组成的非线形分子:转动自由度=3 线形分子:振动自由度=3N5 非线形分子:振动自由度=3N-6
2.基本振动的理论数 对于由N个原子组成的分子: 3N=平动自由度+转动自由度+振动自由度 x y z 由N个原子组成的分子:平动自由度=3 振动自由度= 3N-平动自由度-转动自由度 由N个原子组成的线形分子:转动自由度=2 由N个原子组成的非线形分子:转动自由度=3 线 形 分 子:振动自由度= 3N-5 非线形分子:振动自由度= 3N-6
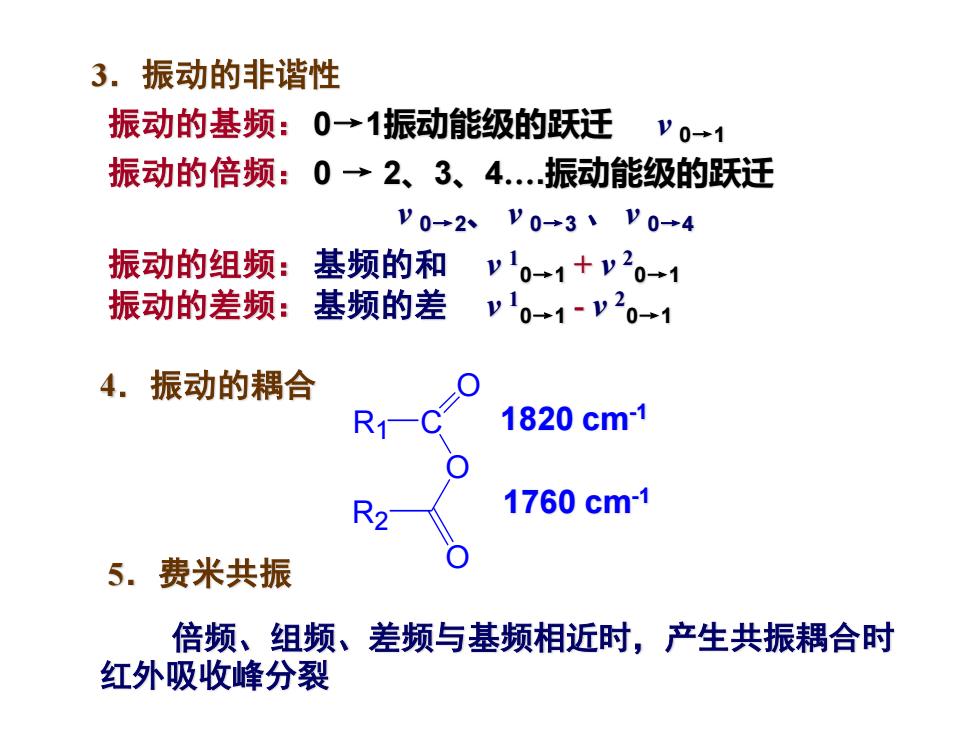
3.振动的非谐性 振动的基频:0→1振动能级的跃迁v0+1 振动的倍频:0→2、3、4.振动能级的跃迁 V0+2V0+3八V0→4 振动的组频:基频的和v'0→1+v20+1 振动的差频: 基频的差v10→1~v20+1 4.振动的耦合 R1—( 1820cm-1 R2 1760cm-1 5.费米共振 倍频、组频、差频与基频相近时,产生共振耦合时 红外吸收峰分裂
3.振动的非谐性 振动的基频:0→1振动能级的跃迁 v 0→1 振动的倍频:0 → 2、3、4.振动能级的跃迁 v 0→2、 v 0→3 、 v 0→4 振动的组频:基频的和 v 1 0→1 + v 2 0→1 振动的差频:基频的差 v 1 0→1 - v 2 0→1 4.振动的耦合 R1 C O O R2 O 1760 cm-1 1820 cm-1 5.费米共振 倍频、组频、差频与基频相近时,产生共振耦合时 红外吸收峰分裂