
第十一章 紫外-可见吸收光谱法 §11.1 分子光谱概述 §11.2光吸收定律 §11.3 紫外-可见分光光度计 §11.4化合物的电子光谱 §11.5紫外-可见分光光度法的应用
§11.1 分子光谱概述 §11.2 光吸收定律 §11.3 紫外-可见分光光度计 §11.4 化合物的电子光谱 §11.5 紫外-可见分光光度法的应用 第十一章
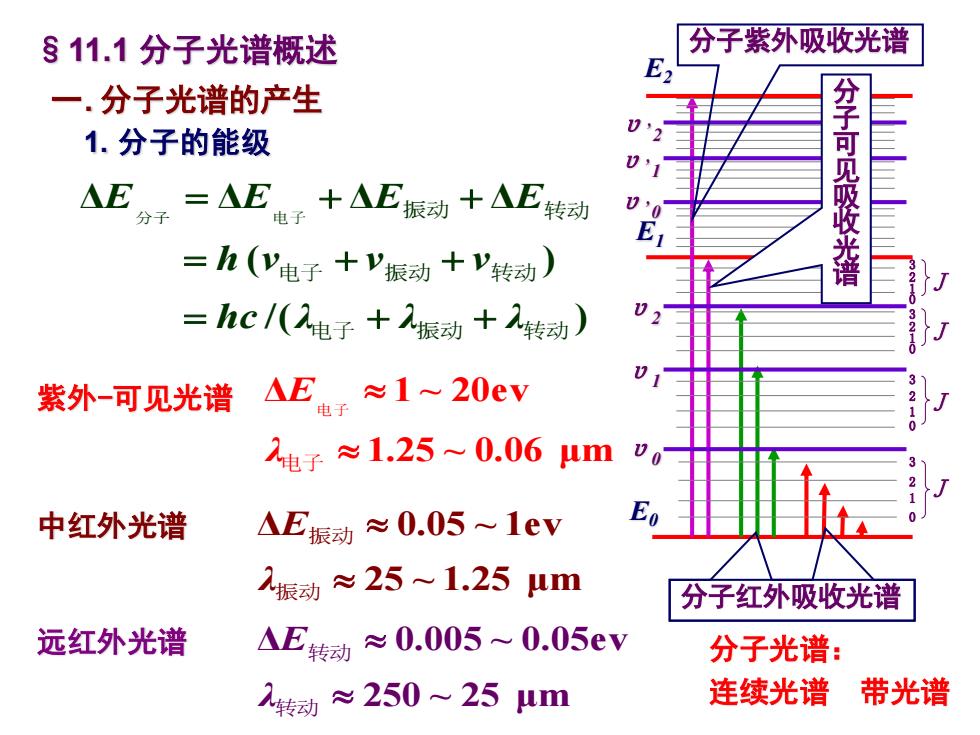
§11.1分子光谱概述 分子紫外吸收光谱 E 一.分子光谱的产生 1.分子的能级 △E分,=AE:十AE振动十AE转动 分子可见吸收光谱 =h(V电子+V振动+V转动) =hc/(2电子+振动+转动) AEr≈1~20ev 01 紫外-可见光谱 2电子≈1.25~0.06um 中红外光谱 △E振动≈0.05~1ev E 振动≈25~1.25m 分子红外吸收光谱 远红外光谱 △E转动≈0.005~0.05eV 分子光谱: 1转动≈250~25um 连续光谱 带光谱
一. 分子光谱的产生 1. 分子的能级 §11.1 分子光谱概述 E2 E1 E0 υ0 υ1 υ2 υ,0 υ,1 υ,2 1 J 023 J 0231 J 0231 J 0231 / ( ) ( ) Δ Δ Δ Δ 电 子 振 动 转动 电 子 振 动 转动 分 子 电 子 振 动 转动 hc λ λ λ h ν ν ν E E E E = + + = + + = + + 分子紫外吸收光谱 分子可见吸收光谱 分子红外吸收光谱 分子光谱: 连续光谱 带光谱 1.25 ~ 0.06 μm Δ 1 ~ 20ev 电 子电 子 λ E 25 ~ 1.25 μm Δ 0.05 ~ 1ev 振 动振 动 λ E 250 ~ 25 μm Δ 0.005 ~ 0.05ev 转动 转动 λ 远红外光谱 E 中红外光谱 紫外 -可见光谱
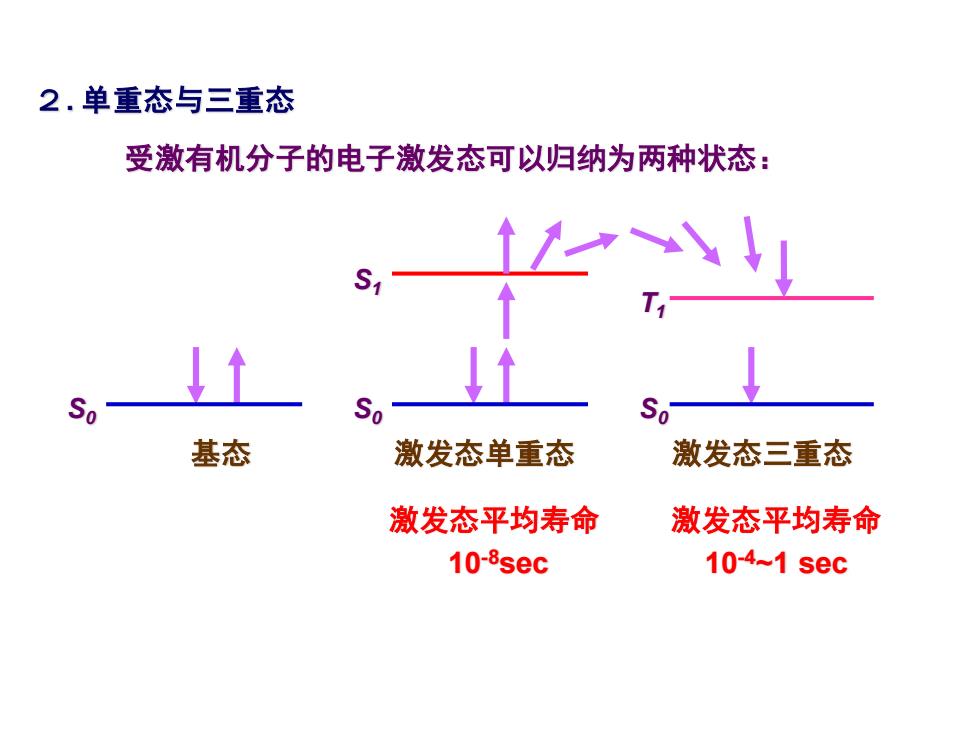
2.单重态与三重态 受激有机分子的电子激发态可以归纳为两种状态: S1 So So So 基态 激发态单重态 激发态三重态 激发态平均寿命 激发态平均寿命 10-sec 10-4~1 sec
2. 单重态与三重态 受激有机分子的电子激发态可以归纳为两种状态: 基态 激发态单重态 激发态三重态 激发态平均寿命 10-8sec 激发态平均寿命 10-4~1 sec S0 S0 S0 S1 T1
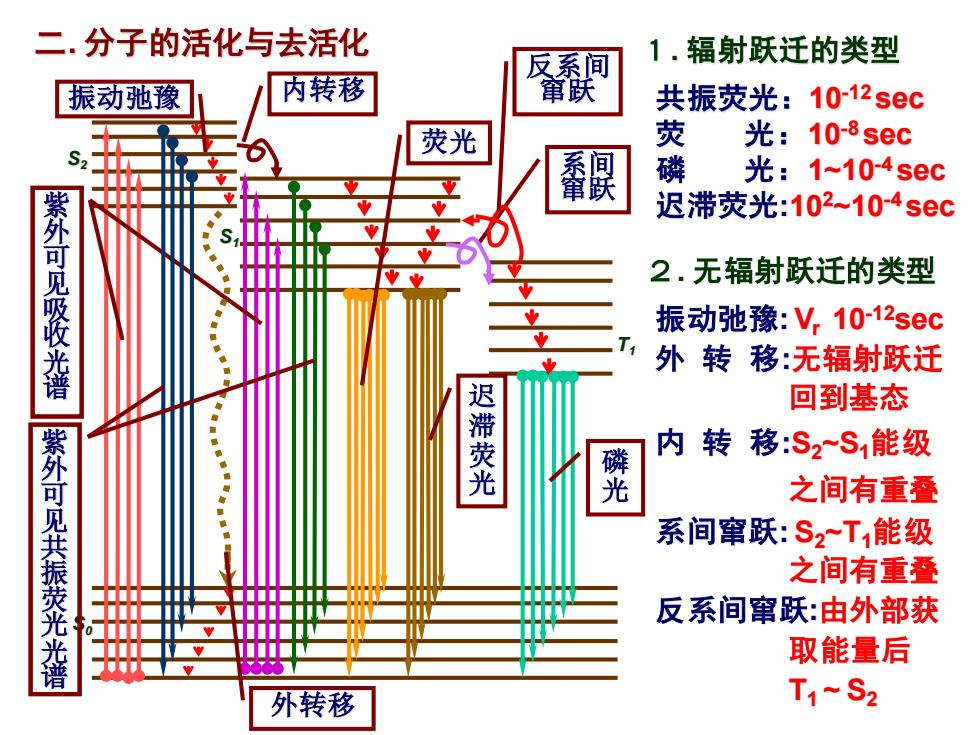
二.分子的活化与去活化 反系间 1.辐射跃迁的类型 振动弛豫 内转移 窜跃 共振荧光:1012sec 荧光 荧 光:10-8sec 系间 磷 光:1~104sec 迟滞荧光:102~104sec 紫外可见吸收光谱 2.无辐射跃迁的类型 振动弛豫:V,1012sec 外转移:无辐射跃迁 迟 回到基态 内转移:S2~S1能级 紫外可见共振荧光光谱 荧光 凳 之间有重叠 系间窜跃:S2T1能级 之间有重叠 反系间窜跃:由外部获 取能量后 外转移 T1~S2
二. 分子的活化与去活化 S0 S1 T1 S2 紫 外 可 见 吸 收 光 谱 外转移 紫 外 可 见 共 振 荧 光 光 谱 内转移 荧光 系间 窜跃 磷 光 反系间 窜跃 迟 滞 荧 光 振动弛豫 2. 无辐射跃迁的类型 振动弛豫: Vr 10-12sec 外 转 移:无辐射跃迁 回到基态 内 转 移:S2~S1能级 之间有重叠 系间窜跃: S2~T1能级 之间有重叠 反系间窜跃:由外部获 取能量后 T1 ~ S2 1. 辐射跃迁的类型 共振荧光:10-12 sec 荧 光:10-8 sec 磷 光:1~10-4 sec 迟滞荧光:102~10-4 sec

§11.2光吸收定律 一.Lambert-Beer定律 1光吸收定律的表达式及其含义 布格(Bouguer)和朗伯(Lambert)先后于1729年和1760 年阐明了光的吸收程度和吸收层厚度的关系: A∝b (动画) 1852年比耳(Beer)又提出了光的吸收程度和吸收物浓 度之间也具有类似的关系: A∝C (动画) 二者的结合称为朗伯比耳定律,其数学表达式为: A=-IgT=-Ig (I/1)=8bc 式中:A:吸光度;T透射率; b:液层厚度(光程长度),通常以cm为单位; c:溶液的摩尔浓度,单位moL; e:摩尔吸光系数,单位Lmo1cm-1;
§11.2 光吸收定律 一. Lambert – Beer 定律 布格(Bouguer)和朗伯(Lambert)先后于1729年和1760 年阐明了光的吸收程度和吸收层厚度的关系: 1852年比耳(Beer)又提出了光的吸收程度和吸收物浓 度之间也具有类似的关系: A ∝ b A ∝ c 二者的结合称为朗伯-比耳定律,其数学表达式为: 式中:A:吸光度;T:透射率; b:液层厚度(光程长度),通常以cm为单位; c:溶液的摩尔浓度,单位mol·L-1; ε:摩尔吸光系数,单位L·mol-1·cm-1; A=- lgT = - lg( It / I0 )= ε b c (动画) (动画) 1.光吸收定律的表达式及其含义
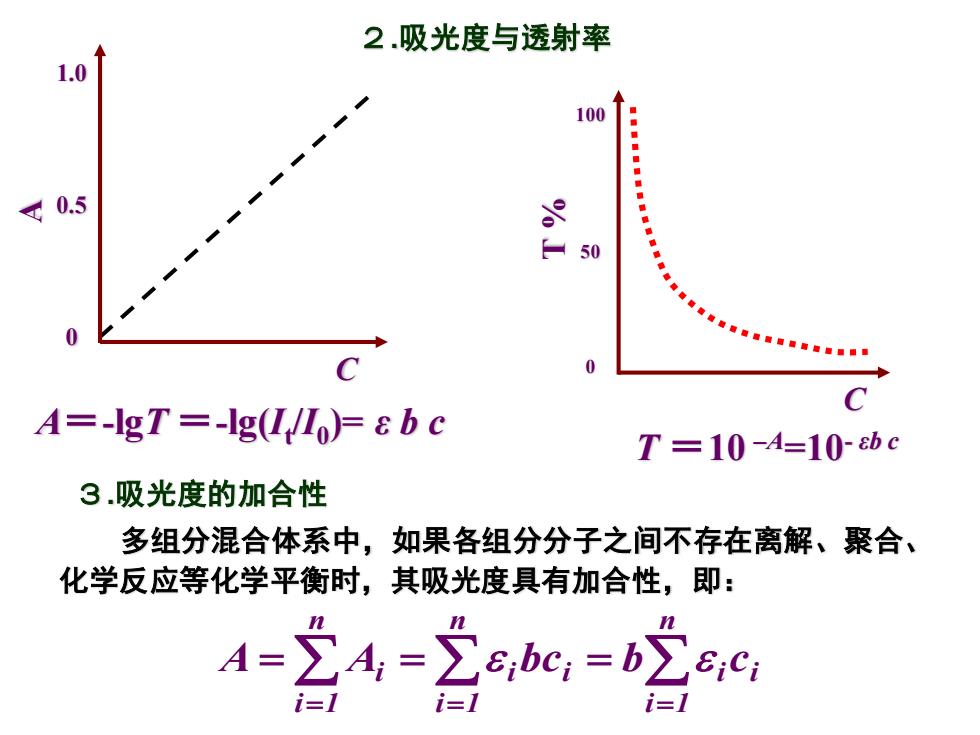
2.吸光度与透射率 1.0 100 ◆ 0.5 9 50 C C A=-IgT =-lg(I/I)=8 b c T=10-A=10bc 3.吸光度的加合性 多组分混合体系中,如果各组分分子之间不存在离解、聚合、 化学反应等化学平衡时,其吸光度具有加合性,即: A=24=2ebc,=bc9 i1
2.吸光度与透射率 A=-lgT =-lg(It /I0 )= ε b c T =10 –A=10- εb c C 1.0 0.5 0 A C 100 50 0 T % 多组分混合体系中,如果各组分分子之间不存在离解、聚合、 化学反应等化学平衡时,其吸光度具有加合性,即: = = = = = = n i 1 i i n i 1 i i n i 1 i A A bc b c 3.吸光度的加合性

3.摩尔吸光系数£ Uy-yis吸收曲线 A=-lgT=8b c 吸光物质的特征常数2);在最大吸收波长)mm处,常以emmx表示 在温度和介质条件一定时,ε仅与吸光物质的结构与性质有关, 可作为定性鉴定的参数; 不随浓度c和光程长度b的改变而改变:=bC/A。 吸光能力与测定灵敏度的度量;emmx越大表明该物质的吸光能力 越强,测定的灵敏度越高。 >105: 超高灵敏;C=A/eb=0.01/105-107mo/L 8=(6~10)×104:高灵敏;C=A/eb-=0.01/5×104=2×10-7mo/L 8×104: 不灵敏。C-A/eb=0.01/104=10-6mol/L &在数值上等于浓度为1mol/L、液层厚度为1cm时该溶液在某一波 长下的吸光度
3. 摩尔吸光系数ε ❖ 吸光物质的特征常数ε(λ);在最大吸收波长λmax处,常以εmax表示 。 ❖ 在温度和介质条件一定时,ε仅与吸光物质的结构与性质有关, 可作为定性鉴定的参数; ❖ 不随浓度c 和光程长度b 的改变而改变:ε= b c / A。 ❖ 吸光能力与测定灵敏度的度量; εmax越大表明该物质的吸光能力 越强,测定的灵敏度越高。 ε>105: 超高灵敏;C= A/ε b =0.01/105=10-7mol/L ε=(6~10)×104 :高灵敏; C= A/ε b =0.01/5 ×104= 2×10-7 mol/L ε<104 : 不灵敏。C= A/ε b =0.01/104= 10-6 mol/L ε 在数值上等于浓度为1 mol/L、液层厚度为1cm时该溶液在某一波 长下的吸光度。 Uv-vis 吸收曲线 A=-lgT =ε b c

4.吸光系数的几种表示方法 A=8bC A=abC 、A=E1mbC C-mol /L C-g/L C-g/100 mL £-摩尔吸光系数 a-吸光系数 EI%1cm-比吸光系数 L·mol-1·cml L'g-1·cm1 100mL·g1·cm-1 &、a、EI%1cm之间的相互换算: Elm=0.1a=0.1 M 二.Beer定律的的局限性 1.仪器偏离 单色光 1.0 正偏离 Lambert-Beer定律的前提条 件之一是入射光为单色光。 负偏离 但实际上难以获得真正意义上 ∠05 的纯单色光。分光光度计只能获得近 乎单色的狭窄光普通带。复合光可导 致对朗伯-比耳定律的正或负偏离
4. 吸光系数的几种表示方法 A = bC C -mol / L ε-摩尔吸光系数 L · mol –1 · cm -1 C-g / L a-吸光系数 L · g –1 · cm -1 A = abC C-g / 100 mL E1% 1cm-比吸光系数 100mL · g–1 · cm -1 A E bC 1% = 1cmM E a 0.1 0.1 1% 、 a、 E1% 1cm之间的相互换算: 1cm = = 二. Beer 定律的的局限性 1.仪器偏离 单色光 Lambert – Beer定律的前提条 件之一是入射光为单色光。 但实际上难以获得真正意义上 的纯单色光。分光光度计只能获得近 乎单色的狭窄光普通带。复合光可导 致对朗伯-比耳定律的正或负偏离。 1.0 0.5 0 A C 正偏离 负偏离

2.浓度的限制 稀溶液 Beer定律的假定:所有的吸光质点之间不发生相互作用; 假定只有在稀溶液(C102mol/L时,吸光质点间可能发生缔合等相互作用,直接 影响了对光的吸收。 溶液中存在着离解、聚合、互变异构、配合物的形成等化学 平衡时。使吸光质点的浓度发生变化,影响吸光度。 3.化学偏离 恒定的化学环境 g.铬酸盐或重铬酸盐溶液中存在下列平衡: CrO2+2H+=Cr20,2+H20 CrO2、Cr2O,2的吸光性质不同,即()不同。此时 溶液pH对测定有重要影响。 4.非均相体系偏离 真溶液 ©g.光吸收定律的假定:溶液必须使均相体系。胶体、乳胶、 悬浮物、沉淀等非均相体系产生的光散射会引起对朗伯- 比耳定律的偏离
2.浓度的限制 稀溶液 Beer定律的假定:所有的吸光质点之间不发生相互作用; 假定只有在稀溶液(C 10-2mol/L 时,吸光质点间可能发生缔合等相互作用,直接 影响了对光的吸收。 溶液中存在着离解、聚合、互变异构、配合物的形成等化学 平衡时。使吸光质点的浓度发生变化,影响吸光度。 e.g. 铬酸盐或重铬酸盐溶液中存在下列平衡: CrO4 2-+2H+ = Cr2O7 2-+H2O CrO4 2-、 Cr2O7 2-的吸光性质不同,即ε(λ)不同。此时 溶液pH对测定有重要影响。 3.化学偏离 恒定的化学环境 e.g. 光吸收定律的假定:溶液必须使均相体系。胶体、乳胶、 悬浮物、沉淀等非均相体系产生的光散射会引起对朗伯- 比耳定律的偏离。 4.非均相体系偏离 真溶液

4.最佳的吸光度测量范围 -In T=8bC 0.4343 dT/T=-8b d C dInT]=-8b dC dC/C=0.4343 d T/(TIgT) a[]-8s,07]-。 0.43434TgT+0.4343=0 (TET) A=-gT=0.4343 T=0.368 当△T=±0.01,即透射率的测量误差为1%时: △C1C×100=0.4343△T/(T1gT×100 =0.4343×(±0.01)/10.368×(-0.4343)1×100 =±2.7% 最佳的吸光度范围:A=0.2~0.8
4.最佳的吸光度测量范围 -ln T =εbC d[lnT] =-εb d C 0.4343 d T/T =-εb d C d C/C= 0.4343 d T/(T lgT) 0 lg Δ 0.4343 C Δ = = T T T T C T ( ) ( ) 0 lg 0.4343Δ lg 0.4343 = + 2 T T T T A=-lgT =0.4343 T =0.368 △ C/C ×100 = 0.4343△ T/(T lgT) ×100 = 0.4343×(±0.01)/[0.368×(-0.4343)] ×100 =± 2.7% 最佳的吸光度范围:A=0.2~0.8 当 △ T= ± 0.01 ,即透射率的测量误差为1%时: