
第六章相平衡 §6-1 相律 §6-2 单组分系统相图 §6-3 二组分理想液态混合物气一液平衡相图 §6-4 二组分真实液态混合物气一液平衡相图 §6-5精镏原理 §6-6 二组分液态部分互溶及完全不互溶系统气一液平衡相图 §6-7二组分液态完全互溶、固态完全不互溶凝聚系统相图 §6-8 二组分液态完全互溶、固态完全互溶或部分互溶凝聚系统 相图 §6-9二组分凝聚系统复杂相图举例 §6-10三组分系统相图简介
第六章相平衡 §6-1 相律 §6-2 单组分系统相图 §6-3 二组分理想液态混合物气—液平衡相图 §6-4 二组分真实液态混合物气—液平衡相图 §6-5 精镏原理 §6-6 二组分液态部分互溶及完全不互溶系统气—液平衡相图 §6-7 二组分液态完全互溶、固态完全不互溶凝聚系统相图 §6-8 二组分液态完全互溶、固态完全互溶或部分互溶凝聚系统 相图 §6-9 二组分凝聚系统复杂相图举例 §6-10 三组分系统相图简介

引言 化工生产中对产物进行分离、提纯,相平衡 可提供理论原理。 用图形来描绘平衡系统的压力、温度及组 成之间的关系,称平衡相图。 本章研究内容: 1、相律: 2、单组分、二组分及三组分相图
引言引言 化工生产中对产物进行分离、提纯,相平衡 可提供理论原理。 用图形来描绘平衡系统的压力、温度及组 成之间的关系,称平衡相图。 本章研究内容: 1、相律; 2、单组分、二组分及三组分相图

§6-1相律 一、 基本概念和术语 1.自由度数: 自由度是用来确定相平衡系统中独立变化的变量。 用F表示。 2.物种数: 化合物的种类数,用$表示。 3.独立化学反应数: 系统中独立化学反应平衡的数目,用R表示
§6-1 相律 一、基本概念和术语 1.自由度数: 自由度是用来确定相平衡系统中独立变化的变量。 用F表示。 2.物种数: 化合物的种类数,用S表示。 3.独立化学反应数: 系统中独立化学反应平衡的数目,用R表示

4.组分数: 用C表示。定义:C=S-R-R',R'是同一相中的浓 度等限定条件。 5.相数: 相是指系统中性质完全相同的均匀部分,化学性 质与物理性质都完全相同,均匀到分子级。相数是系 统中相的数目,用P表示
相是指系统中性质完全相同的均匀部分,化学性 质与物理性质都完全相同,均匀到分子级。相数是系 统中相的数目,用 P表示。 5.相数: 4.组分数: 用 C表示。定义:C=S-R-R′ , R′是同一相中的浓 度等限定条件

相律推导 自由度数=总变量数-总独立方程的个数 假设 S种物质存在于P相的每一相中。 变量: T、p及每一相中有S-1个组成。所以 P个相:总变量数=P(S-1)+2 方程: 每一种物质在各个相中的化学势相等, 即μHB(I)=HB(2)=H(3)片---=HBP), 共SP-1)个;R个独立的化学反应;R'个 独立的浓度限定条件。 总独立方程个数=SP-1)+R+R
二、相律 推导 自由度数=总变量数-总独立方程的个数 假设 S种物质存在于P相的每一相中。 变量: T、p 及每一相中有S-1个组成。所以 P个相: 总变量数=P(S-1)+2 方程: 每一种物质在各个相中的化学势相等, 即μB(1)=μB(2)=μB(3)= ┄ ┄ = μB(P), 共S(P-1)个;R个独立的化学反应;R′个 独立的浓度限定条件。 总独立方程个数=S(P-1)+R+R′

F=[P(S-1)+2]-[S(P-1)+R+R]=S-R-R'-P+2 自由度数 F=C-P+2 F=C-P+n 讨论 1.相律只适用于相平衡系统: 2.推导过程假设$种物质存在于P相的每一相中,若 实际情况不符和仍可适用。 3.F=C-P+n,n=2中的2”通常表示温度、压力; 4对只有液、固相的凝聚系统,忽略压力影响。 F=C-P+1。(C=S-R-R') 5.相律的意义:利用相律来确定描述相平衡系统所 需要的独立变量个数
F=[P(S-1)+2]-[S(P-1)+R+R′]=S-R-R′-P+2 自由度数 F=C-P+2 讨论 5.相律 的意义:利用相律 来确定描述相平衡系统所 需要的独立变量个数。 1.相律 只适用于相平衡系统; 2.推导过程假设 S种物质存在于 P相的每一相中,若 实际情况不符和仍可适用。 3.F=C-P+n, n=2中的“2” 通常表示温度、压力; 4.对只有液、固相的凝聚系统,忽略压力影响。 F=C-P+1 。( C=S-R-R′) F=C-P+n

§6-2 单组分系统相图 相律分析 F=C-P+2 单组分系统:C=1,F=1-P+2=3-P P最小为1,自由度最大为2:自由度最小为0,P最大为3。 1、单组分单相系统:F=2,有两个独立的变量, T、P。可以用面表示系统状态。 2、单组分两相系统:F=1,有一个独立的变量, T、P有数量关系。可以用线表示系统状态。 3、单组三相系统:F=0,无独立的变量, T、P有确定值。可以用点表示系统状态
§6-2 单组分系统相图 相律 分析 F=C-P+2 单组分系统:C=1,F=1-P+2=3-P 1、单组分单相系统:F=2,有两个独立的变量, T、P。可以用面表示系统状态。 2、单组分两相系统:F=1,有一个独立的变量, T、P有数量关系。可以用线表示系统状态。 3、单组三相系统:F=0,无独立的变量, T、P有确定值。可以用点表示系统状态。 P最小为1,自由度最大为2;自由度最小为0,P最大为3

结论 1、单组分系统自由度最小F=0,不能存在四相平衡: 2、单组分系统自由度最大F=2,可以用平面坐标描述。 单组分系统平衡相图 平衡相态: 双变量系统(单相) 单变量系统(两相)无变量系统(三相) 冰 冰·一→水 水 冰·一→水蒸气 冰一→水一→水蒸气 水蒸气 水水蒸气
结论 1、单组分系统自由度最小F=0,不能存在四相平衡; 2、单组分系统自由度最大F=2,可以用平面坐标描述。 单组分系统平衡相图 单组分系统平衡相图 平衡相态: 双变量系统(单相) 单变量系统(两相)无变量系统(三相) 冰 水 水蒸气 冰 水 冰 水蒸气 水 水蒸气 冰 水 水蒸气
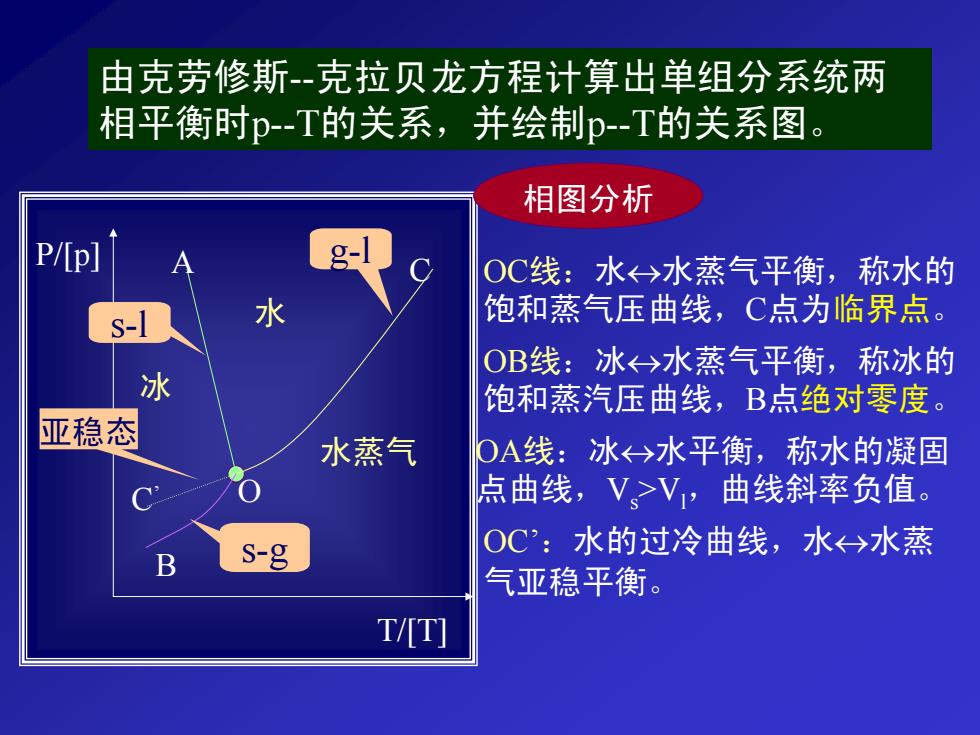
由克劳修斯-克拉贝龙方程计算出单组分系统两 相平衡时p-T的关系,并绘制p-T的关系图。 相图分析 P/p] g- OC线:水←>水蒸气平衡,称水的 水 饱和蒸气压曲线,C点为临界点。 OB线:冰←>水蒸气平衡,称冰的 冰 饱和蒸汽压曲线,B点绝对零度。 亚稳态 水蒸气 OA线:冰←→水平衡,称水的凝固 点曲线,V>V,曲线斜率负值。 S-g OC:水的过冷曲线,水今水蒸 B 气亚稳平衡。 TT]
由克劳修斯--克拉贝龙方程计算出单组分系统两 相平衡时p--T的关系,并绘制p--T的关系图。 P/[p] T/[T] A C B C’ O 水 冰 水蒸气 相图分析 OC线:水↔水蒸气平衡,称水的 饱和蒸气压曲线,C点为临界点。 OB线:冰↔水蒸气平衡,称冰的 饱和蒸汽压曲线,B点绝对零度。 OA线:冰↔水平衡,称水的凝固 点曲线,Vs>Vl,曲线斜率负值。 OC’:水的过冷曲线,水↔水蒸 气亚稳平衡。 g-l s-l s-g 亚稳态

O点:三相点,无变量,水<→冰←→水蒸气三相平衡斯, p=0.610kPa,T=0.01℃。 讨论 静分析: 1、 图中分三块区域,分别代表三个不同的单相 区,即液、固、汽,每个区域为双变量区。 2、图中三条线代表着三个两相平衡单变量系统。 3、三相点与冰的区别: 三相点p=0.610kPa,T=0.01℃,纯物质三相平衡: 冰点p-101.325kPa,T=0℃,饱和了空气的 水←→冰平衡。 动分析:
O点:三相点,无变量,水↔冰↔水蒸气三相平衡, p=0.610kPa,T=0.01℃。 讨论 静分析: 1、图中分三块区域,分别代表三个不同的单相 区,即液、固、汽,每个区域为双变量区。 2、图中三条线代表着三个两相平衡单变量系统。 3、三相点与冰的区别: 三相点p=0.610kPa,T=0.01℃,纯物质三相平衡; 冰点p=101.325kPa,T=0℃,饱和了空气的 水↔ 冰平衡。 动分析: