
目录 4-1多组分系统概述 4-2稀溶液的两个经验定律 4-3偏摩尔量 4=4化学势 4-5气体的化学势 4-6真实气体的逸度 4-7理想液态混合物 4-8理想稀溶液 4-9稀溶液的依数性 4-10真实液态系统与活度 理论与科研结合应用实例 科学家史话 参考书
目 录 4-1 多组分系统概述 4-2 稀溶液的两个经验定律 4-3 偏摩尔量 4-4 化学势 4-5 气体的化学势 4-6 真实气体的逸度 4-7 理想液态混合物 4-8 理想稀溶液 4-9 稀溶液的依数性 4-10 真实液态系统与活度 理论与科研结合应用实例 科学家史话 参考书

Contents 。§4-1 Introduction 。·§4-2 Experimental law of dilute solutions ·§4-3 Partial molar quantities ·§4-4 Chemical potential ·§4-5 Chemical potential of gases ·§4-6 Chemical potential of nonideal gases ·§4-7 Ideal liquid mixtures ·§4-8 Ideal dilute solutions .S4-9 Colligative properties of dilute solution 。·§4-l0 Nonideal liquid system and activity
Contents • §4-1 Introduction • §4-2 Experimental law of dilute solutions • §4-3 Partial molar quantities • §4-4 Chemical potential • §4-5 Chemical potential of gases • §4-6 Chemical potential of nonideal gases • §4-7 Ideal liquid mixtures • §4-8 Ideal dilute solutions • §4-9 Colligative properties of dilute solution • §4-10 Nonideal liquid system and activity

本章基本要求 ·了解混合物与溶液的区别,会各种组成表示之间的换算。 •理解拉乌尔定律、享利定律,掌握其有关计算。 ·了解稀溶液的依数性,并理解其应用。 •理解偏摩尔量及化学势的概念,了解化学势判别式的使用。 •理解理想液态混合物的定义,理解混合性质。 ·了解理想气体、真实气体、理想液态混合物、理想稀溶液 中各组分化学势的表达式。 •理解逸度的定义,了解逸度的计算。 •理解活度及活度系数的概念。了解真实理想液态混合物 真实溶液中各组分化学势的表达式
本章基本要求 •了解混合物与溶液的区别,会各种组成表示之间的换算。 •理解拉乌尔定律、享利定律,掌握其有关计算。 •了解稀溶液的依数性,并理解其应用。 •理解偏摩尔量及化学势的概念,了解化学势判别式的使用。 •理解理想液态混合物的定义,理解混合性质。 •了解理想气体、真实气体、理想液态混合物、理想稀溶液 中各组分化学势的表达式。 •理解逸度的定义,了解逸度的计算。 •理解活度及活度系数的概念。了解真实理想液态混合物、 真实溶液中各组分化学势的表达式

§4-1多组分系统概述 Introduction 多组分系统是由两种或两种以上的物质所组成,多组分系统可以 是单相的或是多相的。 一、 混合物和溶液 Mixtures and solutions 1.混合物:对均匀系统中的各组分B,C,D,)均用同样的标准 态和同样的方法加以研究的多组分系统。 2,溶液:区分均匀系统中的组分为溶剂(A)和溶质B),对溶剂、溶 质用不同的标准态和不同的方法加以研究的多组分均相系统
§4-1多组分系统概述 Introduction 一、混合物和溶液 Mixtures and solutions 多组分系统是由两种或两种以上的物质所组成,多组分系统可以 是单相的或是多相的。 1.混合物:对均匀系统中的各组分(B,C,D,···)均用同样的标准 态和同样的方法加以研究的多组分系统。 2.溶液:区分均匀系统中的组分为溶剂(A)和溶质(B),对溶剂、溶 质用不同的标准态和不同的方法加以研究的多组分均相系统
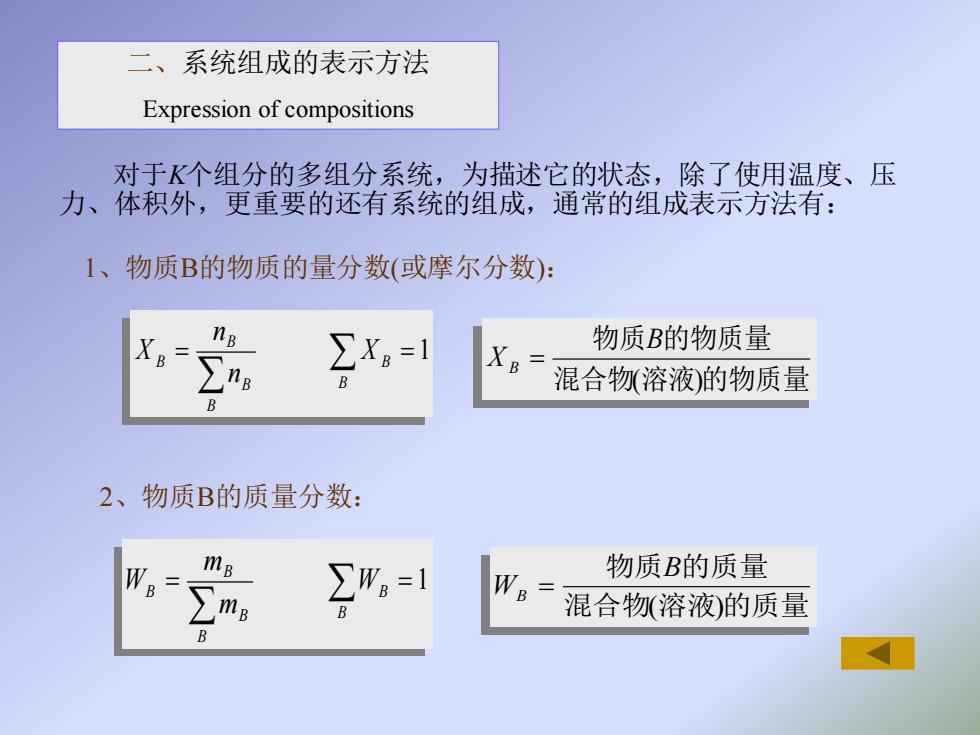
二、系统组成的表示方法 Expression of compositions 对于K个组分的多组分系统,为描述它的状态,除了使用温度、压 力、体积外,更重要的还有系统的组成,通常的组成表示方法有: 1、物质B的物质的量分数(或摩尔分数): ∑X。=1 物质B的物质量 ∑n。 混合物(溶液)的物质量 2、物质B的质量分数: W mB 2- WB 物质B的质量 混合物溶液)的质量
二、系统组成的表示方法 Expression of compositions = = 1 B B B B B B X n n X = = 1 B B B B B B W m m W 混合物 溶液 的物质量 物质 的物质量 ( ) B X B = 混合物 溶液 的质量 物质 的质量 ( ) B WB = 1、物质B的物质的量分数(或摩尔分数): 2、物质B的质量分数: 对于K个组分的多组分系统,为描述它的状态,除了使用温度、压 力、体积外,更重要的还有系统的组成,通常的组成表示方法有:
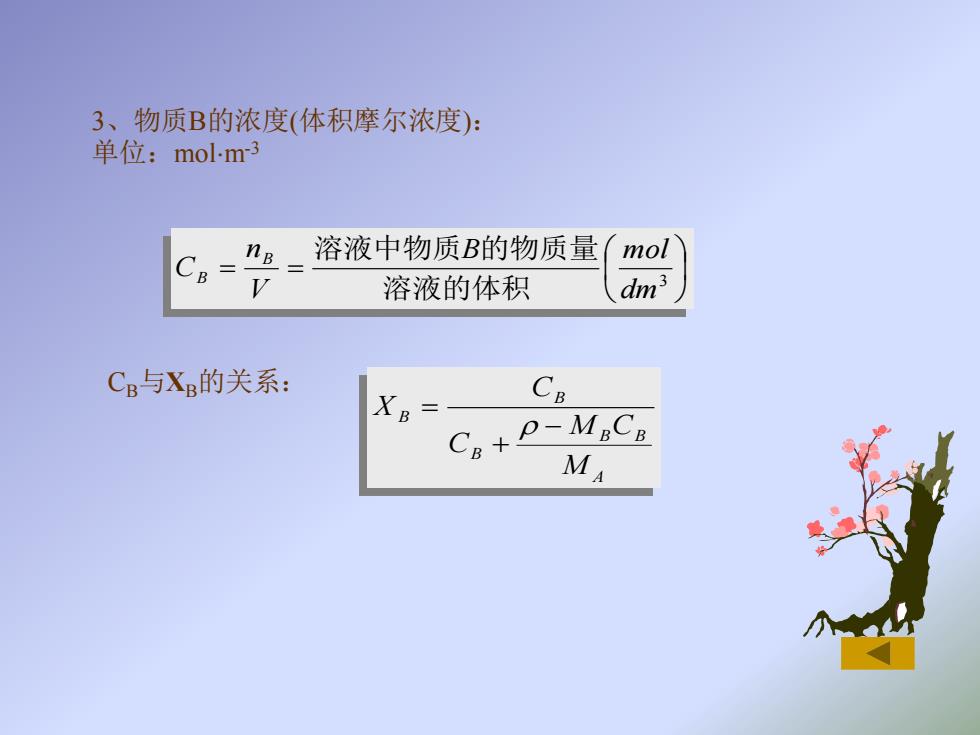
3、物质B的浓度(体积摩尔浓度): 单位:molm3 CB- ng_溶液中物质B的物质量 mol V 溶液的体积 dm3 CB与XB的关系: XB CR Cn+P-MaCa MA
3、物质B的浓度(体积摩尔浓度): 单位:molm-3 CB与XB的关系: A B B B B B M M C C C X − + = = = 3 dm B mol V n C B B 溶液的体积 溶液中物质 的物质量

4、物质B的质量摩尔浓度:b单位:mol.kg1 溶液中物质B的物质量 mol 溶剂的质量 kg bB与XB的关系: bB XB-1+bB MA
4、物质B的质量摩尔浓度:bB 单位:molkg-1 bB与ΧB的关系: B A B B b M b X + = 1 = k g B mol bB 溶剂的质量 溶液中物质 的物质量

§4-2稀溶液的两个经验定律 Expression law of dilute solution 实验证明:非电解质的稀溶液某温度下处于液一气平衡时,液相组 成与气相分压存在着一定的规律,这就是:溶剂服从Raoult?定律,溶质 服从Henry定律。 1886年拉乌尔(Raoult)根据实验得出蒸汽压与组成的关系 拉乌尔定律 Raoult's law 某温度下,溶剂的蒸气分压即⅓等于同温度下纯溶剂的饱 和蒸气压pA与溶液中溶剂的摩尔分数xA之乘积。 PA=PAXA (xA→1)》
§4-2 稀溶液的两个经验定律 Expression law of dilute solution 某温度下,溶剂的蒸气分压pA等于同温度下纯溶剂的饱 和蒸气压pA与溶液中溶剂的摩尔分数xA之乘积。 一、拉乌尔定律 Raoult’s law A A A p p x * = 1886年拉乌尔(Raoult)根据实验得出蒸汽压与组成的关系 实验证明:非电解质的稀溶液某温度下处于液—气平衡时,液相组 成与气相分压存在着一定的规律,这就是:溶剂服从Raoult定律,溶质 服从Henry 定律。 ( xA→1)

1、Raoult定律还可表示为:某温度下溶剂的蒸气压下降△pA (△PA=PA*一PA) 等于同温度下纯溶剂的饱和蒸气压*与溶液中的溶质的 摩尔分数x之乘积。 即:△pA=(PA*一PA)=pA*xB (xB→0) 2、Raoult定律适用于稀溶液,与溶质是否挥发无关
1、Raoult定律还可表示为:某温度下溶剂的蒸气压下降Δ pA (Δ pA= pA* - pA) 等于同温度下纯溶剂的饱和蒸气压pA* 与溶液中的溶质的 摩尔分数xB之乘积。 即:Δ pA = (pA* - pA)= pA* xB ( xB→0) 2、Raoult 定律适用于稀溶液,与溶质是否挥发无关

亨利定律 Henry's law 1803年亨利根据实验得出溶质的蒸汽压与组成的关系: 在一定温度和平衡态下稀溶液中挥发性溶质(B)在气 相中的分压(P)与其在溶液中摩尔分数(X)成正比,称为 亨利定律。 PB-kx.BXB (xB→0) kB单位:Pa 式中k,B一亨利常数,其值与温度、溶剂、溶质有关
在一定温度和平衡态下稀溶液中挥发性溶质(B)在气 相中的分压(PB)与其在溶液中摩尔分数(ΧB)成正比,称为 亨利定律。 二、亨利定律 Henry’s law 1803年亨利根据实验得出溶质的蒸汽压与组成的关系: pB=kx,BΧB kx,B单位:Pa ( →0) B x 式中kx,B—亨利常数,其值与温度、溶剂、溶质有关