
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 第,、章统计热力学初步司题及参考答素 1按照经典的能量均分原理,每摩尔气体分子在各平动自由度上的平动能为)RT。 现有1molC0气体于0℃、latm条件下置于立方容器中,试求: (1)每个C0分子的平均动能E: (2)与E相当的C0分子平动量子数平方和(x2+y2+2). 解:(1)平动自由度数为3,所以,每个C0分子的平均平动能: E=3xRr×2-[侵x13806x10×27315=5657x10y 2)=,k2+y+) 8mv3 C0分子的质量: m=Meo×10-2_2801x10-3) (602205×10西kg=46513x100kg r.R-8314x2735hm-22413x10m p(1.01325×103 k2+yr2+:)-×8m b- _5657x102×8×46513x10x22413x10 =3.811×1020 (6.6218×107 2.某平动能级的x2+y2+:2=45,试求该能级的简并度。 解:因平动量子数x、y、:只能是1、2、3…等正整数,所以,当x2+y2+:2=45 时,三个量子数的取值只能是一个2、一个4及一个5。三个平动量子数的取值各异,所以 该能级的简并度: 8=31=6 即该能级有下列六种平动量子状态 (3、4、5)(42、5)(5、2、4) (2、5、4)(4、5、2)(5、4、2) 3.气体C0分子的转动惯量1=14.5×10”gcm2,试求转动量子数J为4与3两能 级的能量差值△s转及T=30OK时的△s/KT值。 解:E=JJ+8 h TEL:010-64434903
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 1 第八章 统计热力学初步习题及参考答案 1.按照经典的能量均分原理,每摩尔气体分子在各平动自由度上的平动能为 RT 2 1 。 现有 1mol CO 气体于 0℃、1atm 条件下置于立方容器中,试求: (1)每个 CO 分子的平均动能e ; (2)与e 相当的 CO 分子平动量子数平方和( ) 2 2 2 x + y + z 。 解:(1)平动自由度数为 3,所以,每个 CO 分子的平均平动能: 1.38066 10 273.15 J 5.657 10 J 2 1 3 2 1 3 -23 -21 ÷ = ´ ø ö ç è æ = ´ ´ = ´ ´ ´ L e RT (2) ( ) 2 2 2 3 2 2 8 x y z mV h e = + + CO 分子的质量: kg 4.6513 10 kg 6.02205 10 10 28.01 10 10 23 2 3 C = ´ ÷ ÷ ø ö ç ç è æ ´ ´ = ´ = - - L M m O 3 -3 3 5 m 2.2413 10 m 1.01325 10 8.314 273.15 ÷ = ´ ø ö ç è æ ´ ´ = = p RT V ( ) 2 3 2 2 2 2 8 h mV x y z ´ + + = e 20 34 2 3 2 21 20 2 3.811 10 (6.6218 10 ) 5.657 10 8 4.6513 10 (2.2413 10 ) = ´ ´ ´ ´ ´ ´ ´ ´ = - - - 2.某平动能级的 45 2 2 2 x + y + z = ,试求该能级的简并度。 解:因平动量子数 x 、 y 、z 只能是 1、2、3……等正整数,所以,当 45 2 2 2 x + y + z = 时,三个量子数的取值只能是一个 2、一个 4 及一个 5。三个平动量子数的取值各异,所以 该能级的简并度: g = 31 = 6 即该能级有下列六种平动量子状态: (3、4、5)(4、2、5)(5、2、4) (2、5、4)(4、5、2)(5、4、2) 3.气体 CO 分子的转动惯量 40 2 I = 14.5´10 g × cm ,试求转动量子数 J 为 4 与 3 两能 级的能量差值De 转 及T = 300K 时的 De / KT 值。 解: I h J J 2 2 8 ( 1) p e = + 转
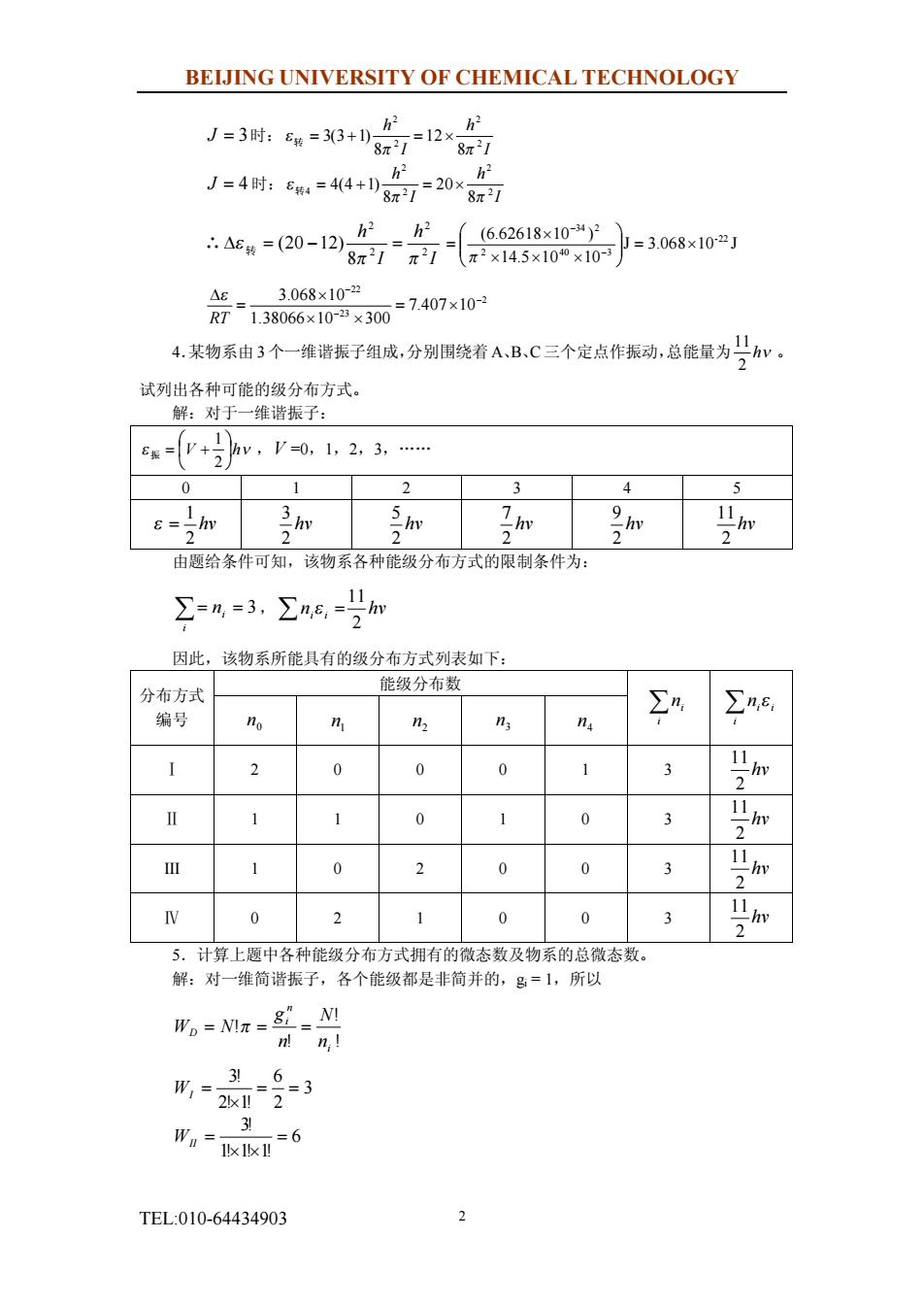
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY J=3时:6#=33+1 、h2 812 8m27 53 ((6.62618×10=3068×102J 4s=20-2子力Fx4w09。 3.068×102 4.某物系由3个一维谐振子组成,分别围绕若A、B、C三个定点作振动,总能量为v。 试列出各种可能的级分布方式。 解:对于一维谐振子: s=(+hv,=0,1,23 … 0 1 2 3 4 5 hy 由题给条件可知,该物系各种能级分布方式的限制条件为: ∑=%=3,∑6号如 因此,该物系所能具有的级分布方式列表如下: 分布方式 能级分布数 ∑n ∑ne 绵号 0 1 3 0 0 0 0 3 2 5.计算上题中各种能级分布方式拥有的微态数及物系的总微态数。 解:对一维简谐振子,各个能级都是非简并的,g=1,所以 =NMx=8=N TEL010-64434903
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 2 J = 3时: I h I h 2 2 2 2 8 12 8 3(3 1) p p e转 = + = ´ J = 4 时: I h I h 2 2 2 2 4 8 20 8 4(4 1) p p e转 = + = ´ ∴ I h I h 2 2 2 2 8 (20 12) p p De 转 = - = J 3.068 10 J 14.5 10 10 (6.62618 10 ) -22 2 40 3 34 2 = ´ ÷ ÷ ø ö ç ç è æ ´ ´ ´ ´ = - - p 2 23 22 7.407 10 1.38066 10 300 3.068 10 - - - = ´ ´ ´ ´ = D RT e 4.某物系由 3 个一维谐振子组成,分别围绕着 A、B、C 三个定点作振动,总能量为 hn 2 11 。 试列出各种可能的级分布方式。 解:对于一维谐振子: e V ÷hn ø ö ç è æ = + 2 1 振 ,V =0,1,2,3,…… 0 1 2 3 4 5 hv 2 1 e = hv 2 3 hv 2 5 hv 2 7 hv 2 9 hv 2 11 由题给条件可知,该物系各种能级分布方式的限制条件为: å= = i i n 3, n hv i i 2 11 å e = 因此,该物系所能具有的级分布方式列表如下: 能级分布数 分布方式 编号 0 n 1 n 2 n 3 n 4 n å i i n å i i i n e Ⅰ 2 0 0 0 1 3 hv 2 11 Ⅱ 1 1 0 1 0 3 hv 2 11 III 1 0 2 0 0 3 hv 2 11 Ⅳ 0 2 1 0 0 3 hv 2 11 5.计算上题中各种能级分布方式拥有的微态数及物系的总微态数。 解:对一维简谐振子,各个能级都是非简并的,gi = 1,所以 ! ! ! ! i n i D n N n g W = N p = = 3 2 6 2! 1! 3! = = ´ WI = 6 1! 1! 1! 3! = ´ ´ WII =

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 3引 形m=2=3 “23 物系总的微观状态数为: 2=W,+Wm+Wm+W-3+6+3+3-15 6在体积为V的立方体客器中有大目的三平动子,其=0KT,计室选 物系在平衡情况下,x2+y2+:2=14的平动能级上粒子的分布数n与基态能级上分布数 之比。 解:平衡态粒子的分布符合玻尔兹曼分布,故 ”即后 因三维平动子基态能级的x=y=:=1,所以 8。=1,(x2+y2+z2)=1+1+1=3 平动子基态能级的能值为 h 6-8mP示+y+:)=3×gmm=03KT 当x2+y2+:2=14时,能级的能值为 B8n示+y产+:)=l4x0IKT=14KT 由于量子化条件的限制,x2+y2+:2=14的能级对应的三个分量数只能是1、2及3 三个数,故 g=3=6 7.若将双原子分子看作一维谐振子,则气体HC1分子与2分子的振动能级间隔分别为 5.94×10丁与0.426×10J。试分别计算25℃时上述两种分子在相邻两振动能级上分布数 之比 解:一维谐振子的多=1 (1)HCI分子 =ee×10 3/-12w5=e=5409x10r0 n. &,e TEL:010-64434903 3
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 3 3 1! 2! 3! = ´ WIII = 3 2! 1! 3! = ´ WIV = 物系总的微观状态数为: W = + + + = 3 + 6 + 3 + 3 = 15 WI WII WIII WIV 6.在体积为 V 的立方体容器中有极大数目的三维平动子,其 0.1KT 8 2 / 3 2 = mV h ,计算该 物系在平衡情况下, 14 2 2 2 x + y + z = 的平动能级上粒子的分布数 n 与基态能级上分布数 n0 之比。 解:平衡态粒子的分布符合玻尔兹曼分布,故 KT KT g e ge n n e e - - = 0 0 因三维平动子基态能级的 x = y = z = 1,所以 1 g0 = ,( ) 1 1 1 3 2 2 2 x + y + z = + + = 平动子基态能级的能值为 0.3KT 8 ( ) 3 8 2 / 3 2 2 2 2 2 / 3 2 0 = + + = ´ = mV h x y z mV h e 当 14 2 2 2 x + y + z = 时,能级的能值为 ( ) 14 0.1KT 1.4KT 8 2 2 2 2 / 3 2 = x + y + z = ´ = mV h e 由于量子化条件的限制, 14 2 2 2 x + y + z = 的能级对应的三个分量数只能是 1、2 及 3 三个数,故 g=3!=6 6 1.997 1 6 1.1 0.3 1.4 0 0 = = = ´ = - - - - - e e e g e ge n n KT KT e e 7.若将双原子分子看作一维谐振子,则气体 HCl 分子与 I2分子的振动能级间隔分别为 5.94×10-10J 与 0.426×10-20J。试分别计算 25℃时上述两种分子在相邻两振动能级上分布数 之比。 解:一维谐振子的 gi = 1 (1)HCl 分子: 10 5.409 10 0 1 1 5.94 20 /1.38066 10 298.15 14.43 7 23 = = = ´ = = ´ » - - ´ ´ - - D - - - + + - e e e g e g e n n KT KT v KT v v v e e e

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY (2)分子: 月u=e音=e0 26-116i0-2915=e-00=3553 8.2molN2置于一容器中,T-400K,P=50kPa,试求容器中N2分子的平动配分函数。 解:m=Mx10 L V=IRT -2)”r-23t2a00” 2×8314×400 (6.62618×104)Y2 50×10° =2.9656×10 9.已知气体l分子相邻振动能级的能值差△=0.426×10-J,试求300K时2分子的 振动特征温度、g及∫ 解:对于相邻的(上、下)两级能级的能值差为:△ε=m 9sem-em。m-em“1672-059800.9309 9%=9s×e9ar=0.9309x1.6277=1.557 因一维简谐振子的自由度数为1,故 f0=9=1.557 10.试求298.15K时氩气的标准摩尔熵S。 解:氩气是单原子气体,不存在振动及转动,故S=S平,对于1ml气体: s=Rn巴am7'.+号K-RhCa'g+R 1h3 1h3 =02“ 8.314T sr-侵nM+h7-np-169 T=298.15K,M=39.948,p=101.325kPa Sme=8312n39948+n29815-11649-mo.K =8314×18.61=154.7J·mo.K TEL010-64434903 4
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 4 (2)I2分子: 3.553 1 0.426 10 /1.38066 10 298.15 1.0349 20 23 = = = = - ´ ´ ´ - D - + - - e e e n n KT v v e 8.2mol N2置于一容器中,T=400K,P=50kPa,试求容器中 N2分子的平动配分函数。 解: L M m 3 10- ´ = P nRT V = 3 3/ 2 34 2 3 23 3/ 2 2 50 10 2 8.314 400 (6.62618 10 ) 2 2 3.14 28 10 1.38006 10 400 ´ ´ ´ ú ´ û ù ê ë é ´ ´ ´ ´ ´ ´ ´ ÷ = ø ö ç è æ = - - - V h mkT qi p =2.9656×1031 9.已知气体 I2分子相邻振动能级的能值差 0.426 10 J -20 De = ´ ,试求 300K 时 I2分子的 振动特征温度、 0 q振 及 0 f振 解:对于相邻的(上、下)两级能级的能值差为: De = hv 振动特征温度: K 308.5K 1.38066 10 0.426 10 23 20 = ÷ ÷ ø ö ç ç è æ ´ ´ = D Q = = - - K K hv e 振 0.9309 1.6722 0.5980 1 1 1 308.5/ 600 308.5/600 / 2 / 2 = - = - = - = Q -Q - e e e e q振 振 T 振 T 0.9309 1.6277 1.557 0 / 2 = ´ = ´ = Q T q q e 振 振 振 因一维简谐振子的自由度数为 1,故 1.557 0 0 f振 = q振 = 10.试求 298.15K 时氩气的标准摩尔熵 + Sm,298 。 解:氩气是单原子气体,不存在振动及转动,故 Sm = S平 + ,298 ,对于 1mol 气体: V R Lh mkT NK R T U V Lh mkT S R m m 2 (2 ) 5 ln (2 ) ln 3 3/ 2 3 3 / 2 = + + = + p p P T Vm 101325 8.314 = , L M m 3 10- ´ = ÷ ø ö ç è æ = + ln - ln -1.1649 2 5 ln 2 3 S平 R M T p T = 298.15K , 39.948 M Ar = , p = 101.325kPa 1 1 ,298, ln 298.15 1.1649 J mol K 2 5 ln 39.948 2 3 8.314 + - - ÷ × × ø ö ç è æ Sm 平 = + - =8.314×18.61=154.7J·mol-1·K -1

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 11.C0的转动惯量1=1.45×106kgm2,振动特征温度⊙泰=3084K,试求298.15时C0 的标准摩尔熵S 解:Mo=28.0104,T=298.15K,P=101325Pa s¥=A2nM+nT-11649=R3h280104+3n29815-11649 =18.078R=150.34J·mo.K T -+R 对称数。=1 h2 08×145x1013806×10=2.77 Sk RIn(l-ewT)+ R⊙E T() 3084-R h+ey+29815 =(0.322×10+3.33×10)R=3.036×10·mo.K S很小与S铁或S相比较可忽略不计 S0%=Sg,S0=150.34+47.19=197,5Jmol.K- 12.含有N个粒子的离域子物系达平衡时,试证: 0A=-K灯h需 证:(1)对于离域子物系 S=NKh是+号+NK=Kag-NnN+N号 根据Strilig公式,当N>1时:-NInN+N=-ln S=kag-h号=Kh名+号 四=KThg' 4-U-=0-k灯h-U=-kTh TEL:010-64434903
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 5 11.CO 的转动惯量 I = 1.45×10-46kg×m 2,振动特征温度Θ振=3084K,试求 298.15 时 CO 的标准摩尔熵 0 Sm,298 。 解: 28.0104 M CO = ,T = 298.15 K, P =101.325kPa ÷ ø ö ç è æ ÷ = + - ø ö ç è æ = + - ln 298.15 1.1649 2 5 ln 28.0104 2 3 ln 1.1649 2 5 ln 2 0 3 S平 R M T R =18.078R=150.34J·mol-1·K -1 R T S R + ×Q = 转 转 s ln 0 对称数s = 1 2.7777K 8 1.45 10 1.38066 10 2 46 23 2 = ´ ´ ´ ´ Q = - - p h 转 0 -1 -1 1 5.676 47.19J mol K 1 2.7777 298.15 ln ÷ = = × × ø ö ç è æ + ´ S转 = R R ( 1) ln(1 ) 0 / 1 - ×Q = - + Q -Q - T T T e R S R e 振 振 振 振 = R e e ú û ù ê ë é - + + - - 298.15( 1) 3084 ln(1 ) 3084/ 298.15 3084/ 298.15 1 = (0.322 10 3.33 10 )R -4 -4 ´ + ´ =3.036×10-3J·mol-1·K -1 0 S振 很小与 0 S转 或 0 S转 相比较可忽略不计 0 0 1 1 298 0 150.34 47.19 197.5J mol K - - + = 平 转 = + = × × , Sm S S 12.含有 N 个粒子的离域子物系达平衡时,试证: (1) ! ln N q A KT N = - (2) T N V q NKTV N q G KT ÷ ø ö ç è æ ¶ ¶ = - + ln ! ln 证:(1)对于离域子物系 ( ) T U NK K q N N N T U N q S NK N = ln + + = ln - ln + + 根据 Strilig 公式,当 N>>1 时: - N ln N + N = -ln N! ∵ ( ) T U N q K T U S K q N N N = - + = + ! ln ln ! ln U N q TS KT N = + ! ln ! ln ! ln N q U KT N q A U TS U KT N N = - = - - = -

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 2)G=4+m:-kTn%+Pr 4--KTIng N! =-NKT Ing+KTIn N! ÷,=-w02) :m==Nmf2) a =-P导出理想气体服从PV=NKT 证:因理想气体为离域子物系 ·A=-kTng =-NKTIng+KTIn N! )., 根据q的析因子性质 lng=ng平+lng转+ln9 对于理想气体 -” hg=h2am7+hr+ha+ng。 上式在T不变的条件下对V求导,得 将(2)式代入(1)式,可得: TEL:010-64434903 6
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 6 (2) PV N q G A PV KT N + ! = + = - ln 由热力学关系式可知: V V A PV T ÷ ø ö ç è æ ¶ ¶ = - ln ln ! ! ln NKT q KT N N q A KT N = - = - + ∴ T V T q NKT V A ÷ ø ö ç è æ ¶ ¶ ÷ = - ø ö ç è æ ¶ ¶ ln T V T q NKTV V A PV V ÷ ø ö ç è æ ¶ ¶ ÷ = ø ö ç è æ ¶ ¶ \ = - ln T N V q NKTV N q G KT ÷ ø ö ç è æ ¶ ¶ \ = - + ln ! ln 13.试由 P V A T ÷ = - ø ö ç è æ ¶ ¶ 导出理想气体服从 PV = NKT 。 证:因理想气体为离域子物系 ∴ ln ln ! ! ln NKT q KT N N q A KT N = - = - + T V T q NKT V A ÷ ø ö ç è æ ¶ ¶ ÷ = - ø ö ç è æ ¶ ¶ ln (1) 根据q 的析因子性质 ln q = ln q平 + ln q转 + ln q振 对于理想气体 V h mKT q ÷ ´ ø ö ç è æ = 3 / 2 2 2p 平 ∴ V q转 q振 h mKT q ln ln ln 2 ln 2 3 ln 2 = + + + p 上式在 T 不变的条件下对 V 求导,得 V V V V q T T ln ln 1 ÷ = ø ö ç è æ ¶ ¶ ÷ = ø ö ç è æ ¶ ¶ (2) 将(2)式代入(1)式,可得: p V NKT V A T ÷ = - = - ø ö ç è æ ¶ ¶

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY :PV NKT 14.用标准摩尔吉布斯自由能函数及标准摩尔焓函数,计算下列合成氨反应在1000K 时的平衡常数。 N2(g)+3H(g) 2NH:(g) 已知数据如下: 物质 (Gr-Uom (H2w-Ua.J·mor /100 N2g】 198.054 8669 H(g) 137.093 8.468 NHj(g) 203.577 9.916 △,H2NH,298.15K)=-46.11k·mo 解:100OK时题给反应 T =2×(-203.577)-(198.054-3×(-137.093)}J·mo =202.179J·mol △Hsk=2AHe(NH,)=-92.22J·molr OK时题给反应 AUn=△Hk-A(Hs-Uan) ={-92.22-(2×9.916-8.669-3×8.468)}k1·mo=.77.979kJ·mor AG1o0AG-Uom+o=124.2J.mol R100-149379 K9=3.255×107 TEL:010-64434903
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434903 7 ∴ PV = NKT 14.用标准摩尔吉布斯自由能函数及标准摩尔焓函数,计算下列合成氨反应在 1000K 时的平衡常数。 N2(g) + 3H2(g) 2NH3(g) 已知数据如下: 物质 K m T m T G U 1000 0, θ , ÷ ÷ ø ö ç ç è æ - - /J·mol-1·K -1 ( Hm U0,m θ ,298 - )/kJ·mol-1 N2(g) 198.054 8.669 H2(g) 137.093 8.468 NH3(g) 203.577 9.916 θ D f Hm (NH3,298.15K)=-46.11 kJ·mol-1 解:1000K 时题给反应 å ÷ ÷ ø ö ç ç è æ - = ÷ ÷ ø ö ç ç è æ - D B B m T m B m T m T C U T C U 0, θ 0, , θ , n ={2×(-203.577)-(-198.054)-3×(-137.093)} J·mol-1 =202.179 J·mol-1 D = 2D ( 3 ) = θ θ H298K f Hm NH -92.22kJ·mol-1 OK 时题给反应 ( ) 0, θ ,298 θ DU0,m = DH298K - D Hm -U m ={-92.22-(2×9.916-8.669-3×8.468)} kJ·mol-1 =-77.979kJ·mol-1 T U T G Gm T U0,m 0,m θ , θ 1000 1000 D + ÷ ÷ ø ö ç ç è æ D - = D D =124.2 J·mol-1 ∴ 14.9379 1000 ln θ 1000 = - D = - R G K q q K =3.255×10-7