
第六章相平衡司题与参考答案 1、在推导相律时,C个组分是否在每一相中都必须存在? 答:在推导相律时,随然假设C个组分在每一相中都存在,但实际某一相 中的组分数即使小于C,限制条件同样随之减少,相律不受影响。 2、指出下列各系统的独立组分数和自由度数: (1) NH4CI(s)部分分解为NH(g)和HCI(g),并达到分解平衡; (2) CaCO3(s)达到分解平衡: (3) C(s)和C0(g)、C02(g)、02(g)在700℃时达到平衡。 [(1)、2,2。(2)、2,1。(3)、2,1.1 3、试用相相律分析,用碳还原金属氧化物M0的反应体系中能否用控制 温度来控制Me的蒸气压? 解:系统中反应: C(s)+MeO(s)=CO(g)+Me(g) 2C0(g)=C02(g)+C(s) 压力平衡: Pueds)=Pcole)+2Pco,(s) 系统中C=5-2-1=2 P=3 F=C-P+2 =3-3-2=1 由于自由度为1,平衡时T、p及各物质浓度等条件中只有一个是独立 变化的,所以指定温度时,压力随之而改变,可以用控制温度来控制M© 的蒸汽压。 4、如何用相律说明两组分气液平衡相图中恒沸点混合物是混合物而不是化 合物 答:二组分气液平衡相图系统恒沸混合物特点是,气相与其平衡的液 相组成如何相同,R=1。 由相律可知: F=C+P+2 =(2-0-2)-2+2 =1 压力确定时,该平衡系统中温度、气、液相组成也恒定,若压力改变 时,平衡系统中温度、气、液相组成也相应改变。所以恒沸点组成随压力
第六章 相平衡习题与参考答案 1、 在推导相律时, C 个组分是否在每一相中都必须存在? 答 :在推导 相 律 时 ,随 然假设 C 个 组 分 在 每 一相中都 存 在 ,但 实 际 某 一 相 中的组分数即使小于 C,限制条件同样随之减少,相律不受影响。 2、 指出下列各系统的独立组分数和自由度数: ( 1) NH4Cl(s)部分分解为 NH3(g)和 HCl(g),并达到分解平衡 ; ( 2) CaCO3(s)达到分解平衡; ( 3) C(s)和 CO(g)、 CO2(g)、 O2(g)在 700℃时达到平衡。 [(1)、 2, 2。 (2)、 2, 1。 (3)、 2, 1。 ] 3、试用相相 律 分 析 , 用 碳 还 原金属 氧 化 物 MeO 的反应体 系 中 能 否 用控制 温度来控制 Me 的蒸气 压 ? 解:系统中反应: C(s)+MeO(s)=CO(g)+Me(g) 2CO(g)=CO2(g)+C(s) 压 力 平衡: pMe(g ) pCO(g ) pCO (g ) 2 = + 2 系统中 C=5-2-1=2 P=3 F=C-P+2 =3-3-2=1 由于自由度为 1, 平衡时 T、 p 及 各 物 质 浓 度 等 条件中 只 有 一 个 是 独 立 变 化的, 所 以 指 定 温度时, 压 力 随 之 而 改 变 , 可 以 用 控 制 温 度 来 控 制 Me 的 蒸 汽 压 。 4、如 何 用 相 律 说 明 两 组 分 气 液 平 衡 相 图 中 恒 沸点混合 物 是 混 合 物 而 不 是 化 合 物 。 答 : 二 组分气 液 平衡相 图 系 统 恒 沸混合 物 特 点 是,气相 与 其 平衡的 液 相 组 成如何 相同, R ‘ =1。 由相律 可 知 : F=C+P+2 =(2-0-2)-2+2 =1 压力确定 时 , 该 平衡系统中温 度 、气、 液 相 组 成也恒定 , 若压力改变 时,平 衡 系统中 温 度 、 气 、 液 相 组 成 也 相 应 改 变 。 所 以恒沸点 组 成 随 压 力

改变而改变。因此,恒沸混合物是混合物而不是化合物。 5、在100kPa下,A、B二组分系统的沸点-组成图 如右图: (1)图中E点对应的温度TE称为什麽温度,此 点对应的气相和液相的组成有何关系? (2)曲线1和曲线4各称为什麽线? (3)总组成在0~XB,E范围内,B组分在气相中的含量与在平衡液相中的 含量有和何关系? 答:()图中E点对应的温度Te称最低恒沸点,此 点对应的气相和液相的组成相等。 (1)曲线1和曲线4各称气相线和液相线。 (2)总组成在0~xB.E范围内,B组分在气相中的含量大于平衡液相中的 含量。 6、某A、B二组分系统在压力p°下的气-液平衡相图 T 如右图。讨论组成为a、b、c、d各点的物系加热 时状态的变化。 答:a点处于A、B部分互溶的两液相层11、12,当加热到最低 共沸点时TE时出现三相平衡即1、2和气相g,继续加热 进入气液两相区,最后进入一相气相区。 Xg b点处于A、B部分互溶的两液相层11、12,当加热到最低 共沸点时TE时出现三相平衡即1、2和气相g,继续加热到T1进入液 相区。 c点同a点相似。 d点处于A、B部分互溶的两液相层11、12,当加热到最低 共沸点时TE时1,消失,同时气相出现,进入气液两相区。继续加热到 T2进入液相区。 7、某二元凝聚物系相图如右图所示。 (1)请指出相图中各区域的相数和相态: (2)指出三相线: (3) 分别从a、b、c、d、e、f点绘制步冷曲线: (4) 指出系统沿每条步冷曲线的相态变化。 (略)
改变而改变 。 因 此 , 恒沸混合 物 是 混 合 物 而 不是化 合 物 。 5、 在 100 kPa 下 , A、 B 二 组分系统的 沸 点 -组 成 图 如右图 : (1) 图 中 E 点 对 应的温度 TE 称 为 什 麽 温度, 此 点 对 应的气相和 液 相的组 成有何关 系 ? (2) 曲 线 1 和 曲 线 4 各 称 为 什麽线 ? (3) 总 组 成 在 0~ x B, E 范围内 ,B 组分在 气 相中的 含量与 在 平 衡 液 相 中 的 含量有 和 何 关 系 ? 答 : (1)图 中 E 点 对 应的温度 TE 称最低恒沸点 , 此 点 对 应的气相和 液 相的组 成 相 等 。 (1) 曲 线 1 和 曲 线 4 各 称 气 相 线 和 液 相 线 。 (2) 总 组 成 在 0~ x B, E 范围内 ,B 组 分 在 气 相 中 的 含量大 于 平 衡 液 相 中 的 含 量 。 6、 某 A、 B 二 组分系统在 压 力 p Æ下的气 -液 平衡相 图 如右图 。 讨 论 组 成 为 a、 b、 c、 d 各 点 的物系 加 热 时 状 态 的 变 化 。 答 : a 点 处 于 A、 B 部 分 互 溶 的 两 液 相 层 l 1、 l 2, 当加热 到 最 低 共沸点 时 TE 时 出 现 三 相平衡即 l 1、 l 2 和气相 g, 继续加热 进 入 气 液 两 相 区 , 最后进入 一相气相 区 。 b 点 处 于 A、 B 部 分 互 溶 的 两 液 相 层 l 1、 l 2, 当加热 到 最 低 共沸点 时 TE 时 出 现 三 相 平衡即 l 1、 l 2 和 气 相 g, 继 续 加 热 到 T1 进入液 相 区 。 c 点 同 a 点 相 似 。 d 点 处 于 A、 B 部 分 互 溶 的 两 液 相 层 l 1、 l 2, 当加热 到 最 低 共沸点 时 TE 时 l 1 消 失 , 同 时 气相出 现 , 进 入 气 液 两 相 区 。 继 续 加 热 到 T2 进入液 相 区 。 7、 某 二元凝聚 物系相 图如右图所示 。 ( 1) 请 指出相 图 中 各 区 域 的相数和相 态 ; ( 2) 指 出 三 相 线 ; ( 3) 分 别 从 a、 b、 c、 d、 e、 f 点 绘 制 步 冷 曲 线 ; ( 4) 指出系统 沿 每 条 步 冷 曲 线 的 相 态 变 化 。 (略 ) T xB A a b c d A x B B T C f e d c b a

8、A-B合金相图如右图。图中PE、QE可分别称做 A与B凝固点下降曲线,该曲线能否用凝固点下 降公式计算求得?为什麽? 答:该曲线不能用凝固点下降公式计算求得。 不是稀溶液。 A X 9、已知铋的熔点为544.5K,镉的熔点为594K,铋与镉的低共熔温度为 T=408K,铋的摩尔溶化热为10.88 kJ-mol,镉的摩尔溶化热为6.07 kJ.mol,设溶液是理解的。试计算低共熔混合物的组成。 解:由凝固点降低公式: dlnx-△化H dr RT2 将如上公式应用于铋,设共熔混合物中铋的含量以摩尔分数表示为x: 假设△紫化Hm与温度无关。当X=1时为纯铋。 由积分公式得: x=0.44 10、苯和萘的熔点分别为5.5℃和79.9℃,摩尔溶化热分别为9.837 kJ.mol和19.08k小mol,苯和萘可形成低共熔混合物的固相完全互溶系 统,求出该体系的低共熔点的组成和温度。并绘出草图相图。 解:设苯和萘的组成分别为x1和2,苯和萘的溶化热与温度无关。由凝固 点下降公式: : -(1) 9837(11 8.314279T -(2) -19080(11 8.314353T
8、 A-B 合 金 相 图如右图 。 图 中 PE、 QE 可 分 别 称 做 A 与 B 凝 固 点 下 降 曲 线 , 该曲线 能否用 凝 固 点 下 降公式计算求得 ? 为 什 麽 ? 答 : 该曲线 不能用 凝 固 点 下 降公式计算求得 。 不 是 稀 溶 液 。 9、 已 知 铋 的 熔 点 为 544。 5K, 镉 的 熔 点 为 594K, 铋 与 镉 的 低 共 熔 温 度 为 Tf=408K, 铋 的 摩 尔 溶 化 热 为 10。 88kJ·mol- 1 , 镉 的 摩 尔 溶 化 热 为 6。 07 kJ·mol-1 ,设 溶 液 是 理 解的。试 计 算 低 共 熔 混 合 物的组 成 。 解:由 凝 固 点 降 低 公 式 : 2 ln RT H dT d x D溶化 m = 将 如 上 公 式 应 用 于 铋 ,设 共 熔 混 合 物 中 铋 的 含量以 摩 尔 分 数 表 示 为 x。 假 设 Δ 溶 化 Hm 与 温 度 无 关 。 当 x=1 时 为 纯 铋 。 由 积 分 公式得 : x=0.44 10、 苯 和 萘 的 熔 点 分 别 为 5。 5℃ 和 79。 9℃ , 摩 尔 溶 化 热 分 别 为 9。 837 kJ·mol- 1 和 19。 08 kJ·mol- 1 ,苯 和 萘 可 形 成 低 共 熔 混 合 物 的 固 相 完 全 互 溶 系 统 , 求 出 该 体系的 低 共 熔 点 的 组 成 和温度。并 绘 出 草 图 相 图 。 解:设 苯 和 萘 的 组 成 分 别 为 x1 和 x2 ,苯 和 萘 的 溶 化 热 与 温 度 无 关 。 由 凝 固 点 下 降公式 : 苯 : ÷ ø ö ç è æ = - ÷ ÷ ø ö ç ç è æ - D = T R T T H x f f m 1 279 1 8.314 9837 1 1 ln 1 * 苯 溶化 苯 --------------------------(1) 萘 : ÷ ø ö ç è æ = - ÷ ÷ ø ö ç ç è æ - D = T R T T H x f f m 1 353 1 8.314 19080 1 1 ln 2 * 萘 溶化 萘 ------------------------(2) A B xB T E P Q

由(1)(2)联立得解低共熔点组成和温度: x=0.865 T=.3C 11、A液体的正常沸点为338K,其气化热为34.727kJ·mol1.A液体和B 液体可形成理想液态混合物。今将1mol的A与9mol的B混合形成理想液 态混合物,其沸点为320K。试计算: (1)将组成xA=0.4的这种混合形成理想液态混合物置于带活塞的汽缸内, 开始时活塞与汽缸接触,若在320K下渐渐降低活塞的压力,当液体内 出现第一个气泡时,气相组成y=?气相总压pa=? (2)若将活塞上的压力继续减压,溶液在恒温320K下继续气化,当最后只 剩下一滴液体时,这一滴液体组成气相组成yA=?气相总压P悬=? 解:(1) 设气化热为一常数。 由克劳修斯一克拉贝龙方程计算320K时A的饱和蒸汽压: hP=-△eH1-1) P R(T2T h101.325-3472z11 8.314320338 h101325 PA 101325=2.004 P P=50.56kPa 320K时,pe=101.325kPa p4=px4=50.56×0.lkPa=5.056kPa Pa=Pa-P4=(101.325-5.056)kPa=96.269kPa pi=坠=96269tra=10696Pa X 0.9 当xB=0.4时: p4=pAx4=50.56×0.4kPa=20.22kPa PB=PB·xB=106.96×0.6kPa=64.18kPa Pe=P4+P=(20.22+64.18)kPa=84.396kPa y=2=202=02396 P总84.396
由 (1)(2)联 立 得 解 低 共 熔 点 组 成 和温度: x=0.865 T=-3℃ 11、A 液 体 的 正 常 沸 点 为 338K,其 气 化 热 为 34。727kJ·mol- 1 .A 液 体 和 B 液 体 可 形 成 理 想 液 态混合 物 。今 将 1mol 的 A 与 9mol 的 B 混 合 形 成 理 想 液 态混合 物 , 其沸点 为 320K。 试 计 算 : (1) 将 组 成 x A=0.4 的 这 种 混 合 形 成 理 想 液 态混合 物 置 于 带 活 塞 的 汽 缸 内 , 开 始 时 活 塞 与 汽 缸 接 触 , 若 在 320K 下 渐 渐 降 低 活 塞 的 压 力 , 当 液 体 内 出 现 第 一个气 泡 时,气相组 成 yA=?气相 总 压 p 总 =? (2) 若 将活塞上 的 压 力 继 续 减 压 , 溶 液 在 恒 温 3 20K 下 继 续 气化, 当 最后只 剩 下 一 滴 液 体时, 这 一 滴 液 体 组 成 气相组 成 yA=?气相 总 压 p 总 =? 解 : (1) 设气化 热 为 一 常 数 。 由 克劳修斯 —克拉贝龙方程计算 320K 时 A 的 饱 和 蒸 汽 压 : p kPa p p p R T T H P p A A A A m A A 50.56 2.004 101.325 101.325 ln 338 1 320 1 8.314 101.325 34727 ln 1 1 ln * ,1 * ,1 * ,1 * ,1 2 2 * ,1 * ,2 = = = ÷ ø ö ç è æ = - - ÷ ÷ ø ö ç ç è æ - D = - 气化 320K 时 , p 总 =101.325kPa ( ) kPa kPa x p p p p p kPa kPa p p x kPa kPa B B B B A A A A 106.96 0.9 96.269 101.325 5.056 96.269 50.56 0.1 5.056 * * = = = = - = - = = × = ´ = 总 当 xB=0.4 时 : 0.2396 84.396 20.22 (20.22 64.18) 84.396 106.96 0.6 64.18 50.56 0.4 20.22 * * = = = = + = + = = × = ´ = = × = ´ = 总 总 p p y p p P kPa kPa p p x kPa kPa p p x kPa kPa A A A B B B B A A A
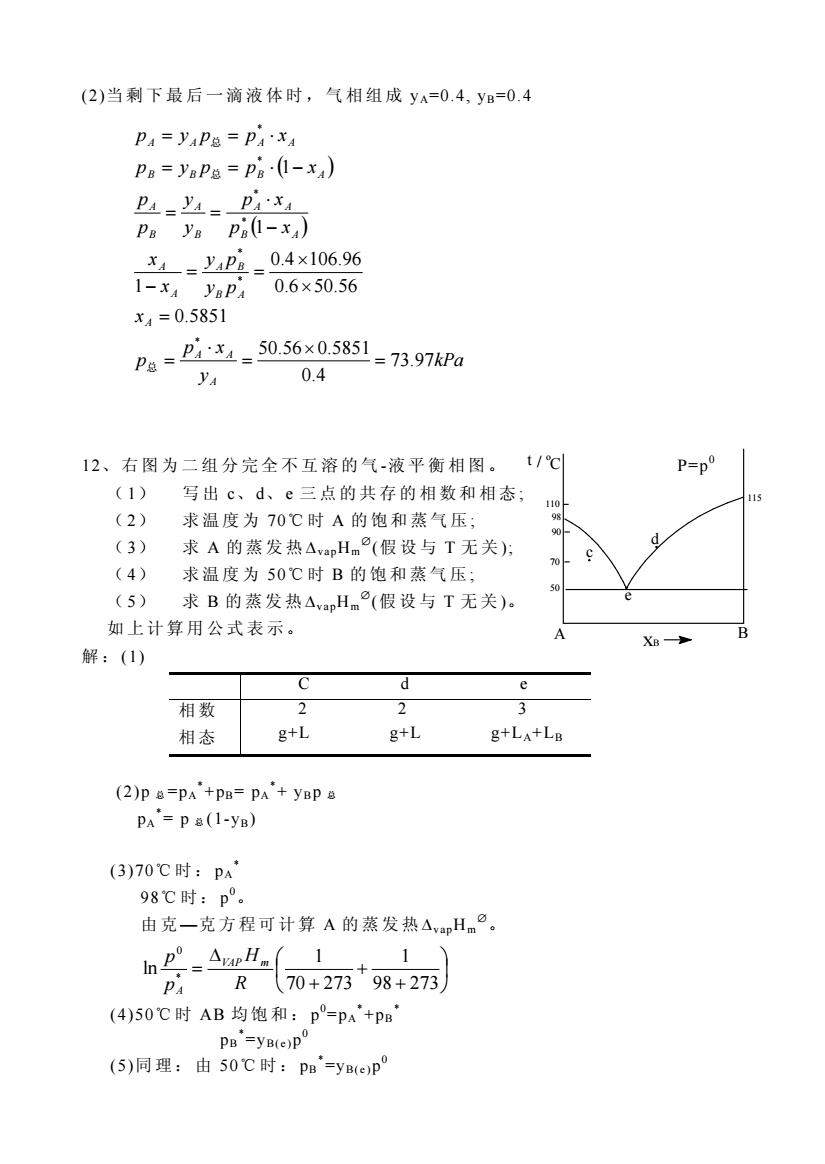
(2)当剩下最后一滴液体时,气相组成yA=0.4,yB=0.4 P4=y4P总=PAxA P8=YaP8=Pa(1-x) PA'xA Pa ya pa(1-x) x1=yP立_04×106.96 1-x4 yaPa 0.6×50.56 x4=0.5851 Pe=D:=5056x05851-73.97a ya 0.4 12、右图为二组分完全不互溶的气-液平衡相图。t/℃ (1) 写出c、d、e三点的共存的相数和相态; (2) 求温度为70℃时A的饱和蒸气压; (3) 求A的蒸发热△vapHm(假设与T无关): (4) 求温度为50℃时B的饱和蒸气压; (5) 求B的蒸发热△vapHm(假设与T无关)。 如上计算用公式表示。 XB- 解:(1) C d e 相数 2 2 相态 g+L g+L g+LA+LB (2)p &=PA'+PB=PA'+yBP a PA'=pa(1-yB) (3)70C时:pA 98℃时:p°。 由克一克方程可计算A的蒸发热△vapHm°。 h.41 R70+27398+273 (4)50C时AB均饱和:p°=pA'+pB PB =yB(e)p (5)同理:由50℃时:PB=yBeP
(2)当 剩 下 最 后 一 滴 液 体时,气相组 成 yA=0.4, yB=0.4 ( ) ( ) kPa y p x p x y p y p x x p x p x y y p p p y p p x p y p p x A A A A B A A B A A B A A A B A B A B B B A A A A A 73.97 0.4 50.56 0.5851 0.5851 0.6 50.56 0.4 106.96 1 1 1 * * * * * * * = ´ = × = = ´ ´ = = - - × = = = = × - = = × 总 总 总 12、 右 图 为 二 组 分 完 全 不 互 溶 的 气 -液 平衡相 图 。 P=p 0 ( 1) 写 出 c、 d、 e 三 点 的 共 存的相数和相 态 ; ( 2) 求 温度为 70℃ 时 A 的 饱 和蒸气 压 ; ( 3) 求 A 的 蒸 发 热 DvapHm Æ (假 设 与 T 无 关 ); ( 4) 求 温度为 50℃ 时 B 的 饱 和蒸气 压 ; ( 5) 求 B 的 蒸 发 热 DvapHm Æ (假 设 与 T 无 关 )。 如 上计算 用 公式表 示 。 解 : (1) C d e 相 数 相 态 2 2 3 g+L g+L g+LA+LB (2)p 总 =pA * +pB= pA * + yBp 总 pA * = p 总 (1-yB) (3)70℃时: pA * 98℃时: p 0。 由 克 —克方程 可 计 算 A 的 蒸 发 热 DvapHm Æ。 ÷ ø ö ç è æ + + + D = 98 273 1 70 273 1 ln * 0 R H p p VAP m A (4)50℃ 时 AB 均 饱 和 : p 0 =pA * +pB * pB * =yB( e )p 0 (5)同 理 : 由 50℃时: pB * =yB( e )p 0 A B xB t 50 70 90 110 / o C 98 115 c d e

115℃时:p° 由由克一克方程可计算B的蒸发热△vapHm. 1 R(50+273+115+273 13.水和乙酸乙酯可部分互溶,在37.55℃互相平衡的两液相中,水层 相酯的浓度X。=0.0146,另一相酯的浓度为X。'=0.8390。已知该温度下 纯水与酯的蒸汽压分别为P◆*=6.40kPa,P需=15.47kPa,设拉乌尔定律对每 相溶剂均适用,并且对水层相酯(X=0.0146)中的酯服从亨利定律,蒸汽 可视为理想气体。 ()计算与两液相平衡的汽相组成。 (2)今有水于乙酸乙酯的气液混合物共200mol,其中水与酯各100mol,在 37.55℃时达到平衡,已知气相量为40mol,试计算每个液相的物质的 量(mol)。 (3)上述第2题所述系统保持37.55℃时,继续蒸发,(不取走蒸汽),哪 一液相先消失,此气相量与液相量各为多少? (4)求水层相酯(仪需=0.0146)的亨利常数。 解:(1)P题=P120x20+P霸x届'=6.40(1-0.0146)+15.46×0.8390 =19.286kPa 汽相组成 a21546x08390=0630 19.286 (2)对酯进行物料恒算 100mol=40×0.673+n*相×0.0146+(160-n*相)×0.8390 得n本相=74.187mol n属m=160-74.187=85.812mol (3)酯相先消失 由杠杆规则,n本m'(0.5-0.0146)=(200-n本m)(0.673-0.5) 得n本相'=52.55mol nm=200-52.55=147.45m0l (4)P霸=kx,己知P酯=15.47×0.839=0.0146k .k=889 KPa 14.已知下列反应: FeO(s)+CO(g)=Fe(s)+CO2(g)
115℃时: p 0 . 由 由 克 —克方程 可 计 算 B 的 蒸 发 热 DvapHm Æ。 ÷ ø ö ç è æ + + + D = 115 273 1 50 273 1 ln * 0 R H p p VAP m B 13. 水 和 乙 酸 乙 酯 可 部 分 互 溶 , 在 37.55 ℃ 互 相 平 衡 的 两 液 相中, 水 层 相 酯 的 浓 度 X 酯 =0.0146, 另 一 相 酯 的 浓 度 为 X 酯 ’=0.8390。 已 知 该 温度下 纯 水 与 酯 的 蒸 汽 压 分 别 为 P* 水 =6.40kPa , P* 酯 =15.47kPa,设 拉乌尔 定 律 对 每 相 溶 剂 均 适 用,并 且 对 水 层 相 酯 (X 酯 =0.0146)中 的 酯 服 从 亨 利 定 律 , 蒸 汽 可 视 为 理 想 气体。 (1) 计 算 与两液 相平衡的 汽 相 组 成 。 (2) 今 有 水 于 乙 酸乙酯 的 气 液 混 合 物 共 200mol, 其 中 水 与 酯 各 100mol ,在 37.55 ℃ 时 达 到 平 衡 , 已 知 气 相 量 为 40mol, 试 计 算 每 个 液 相 的 物 质 的 量 ( mol)。 (3) 上述第 2 题 所 述 系 统 保 持 37.55 ℃时, 继 续 蒸 发 ,( 不 取 走 蒸 汽 ), 哪 一 液 相 先 消 失 , 此 气 相 量与液 相 量 各 为 多 少 ? (4) 求 水 层 相 酯 (X 酯 =0.0146)的 亨利常 数 。 解 : (1) P 总 =PH2O * xH2O+P 指 * x 酯 ’=6.40(1-0.0146)+15.46×0.8390 =19.286 kPa 汽 相 组 成 (2) 对 酯 进 行 物 料 恒 算 100mol=40×0.673+n 水 相 ×0.0146+(160-n 水 相 )×0.8390 得 n 水 相 =74.187 mol n 酯 相 =160-74.187=85.812 mol (3) 酯 相 先 消 失 由 杠 杆规则 , n 水 相 ’(0.5-0.0146)=(200- n 水 相 ’)(0.673-0.5) 得 n 水 相 ’=52.55 mol n 气 相 =200-52.55=147.45 mol (4) P 指 =kx 酯 , 已 知 P 酯 =15.47×0.839=0.0146 k ∴ k=889 KPa 14. 已 知 下列反应: FeO(s)+CO(g)= Fe(s)+ CO2(g) ① 0.6730 19.286 15.46 0.8390= 总 酯 酯 ´ = = P P y

Fe304(s)+CO(g)=3Fe0(s)+C02(g) ② 的标准平衡常数分别为K、K),它们与温度的关系如下 T/K K9 K9 873 0.871 1.15 973 0.678 1.77 设反应的△Cpn均为零。试求: (1)反应①和反应②的标准摩尔反应焓△,H及△,H2: (2)在什么温度下,Fe(s)、Fc0(s)、Fe304(s)、CO(g)、C0(g)全可共存于 平衡系 统中: (3)上述两反应达平衡后,若温度再上升时,系统中哪些物质可能消失? 解:(1)由题意△,Cm=0,可知:均与温度无关,可视为常数。 对同一反应,不同温度下的平衡常数可计算出标准摩尔反应焓: A,H0(11 In K= R(873973 对板应0:会器(品扇 解得:△,H=17.69kJmo1 R(873973 对版”会器扇 解得:△,H2=-30.45/mol (2)设两反应平衡共存时温度为T,且温度为T时K=K,。 由lnK=lnK得:
Fe3O4(s)+CO(g)= 3FeO(s)+ CO2(g) ② 的 标 准 平 衡 常 数 分 别 为 0 2 0 K1、K , 它 们 与 温度的 关 系 如 下 : T/K 0 K1 0 K2 873 0.871 1.15 973 0.678 1.77 设反应的 DrCp,m 均 为 零 。 试 求 : (1) 反 应 ① 和反应 ② 的 标 准 摩 尔 反 应 焓 Dr Hm 0 ,1及Dr Hm 0 ,2; (2) 在 什 么 温 度 下 , Fe(s)、 FeO(s)、 Fe 3O4 (s)、 CO2(g) 、 CO(g)全 可 共 存 于 平衡系 统中; (3) 上 述 两 反应达平衡 后 , 若 温 度 再 上 升 时,系统中 哪 些 物 质 可 能 消 失 ? 解 : (1)由 题 意 DrCp,m =0,可 知 : 均 与 温 度 无 关 , 可 视 为 常 数 。 对 同一反应,不同温度下的平衡 常 数 可 计 算 出 标 准 摩 尔 反 应 焓 : 对 反 应 ① : 1 ,1 0 ,1 0 ,1 0 973 0 873 17.69 973 1 873 1 0.678 8.314 0.871 ln 973 1 873 1 ln - D = × ÷ ø ö ç è æ - D = - ÷ ø ö ç è æ - D = - H kJ mol H R H K K o r m r m r m 解得: 对 反 应 ② : 1 ,2 0 2 0 2 0 973 0 873 30.45 973 1 873 1 1.77 8.314 1.15 ln 973 1 873 1 ln - D = - × ÷ ø ö ç è æ - D = - ÷ ø ö ç è æ - D = - H kJ mol H R H K K o r m r m r m 解得: (2)设 两 反应平衡 共 存时温度为 T, 且 温度为 T 时 0 2 0 K1 = K 。 由 0 2 0 1 ln K = ln K 得 ;

h0871-1769x10'(g-)=h115-3045x10'g-) 8.314T873 8.314T873 解得:T=754K (4)反应①为吸热反应,反应②为放热反应。上述两反应达平衡后,若温 度再上升时,系统中FcO(s)可能消失
T K T T 754 873 1 1 8.314 30.45 10 ln1.15 873 1 1 8.314 17.69 10 ln 0.871 3 3 = ÷ ø ö ç è æ - - ´ ÷ = - ø ö ç è æ - ´ - 解得: (4) 反 应 ① 为 吸 热 反应,反应 ② 为 放 热 反应。 上 述 两 反应达平衡 后 , 若 温 度 再 上 升 时,系统中 FeO(s)可 能 消 失