
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 第二章热力学第一定梓司题及参考答素 1.5mol理想气体于始态1,=-25℃、P,=101.325kPa、恒温膨胀至末态,已知末态体 积了,=2业,分别计算气体膨胀时反抗恒定外压p(环)=0.5p,及进行可逆膨胀时系统所作 的功,并在PV图上给出两种不同途径的功所对应的面积。 解: 理想气体5mol 理想气体5mol 41=25℃ p,=101.325kPa V2=2g ().反抗恒定外压p环)=0.5p,膨胀: 5-nR-3x8314x29815hm=1223m p101.325 W=-p环%3-V)=(-0.5x101.325x122.32)=6.197kJ (2).可逆膨胀: 期=-n-气5x83429815n}=-839则 2.1mol理想气体由202.66kPa、10dm3恒温升温,使压力升到2026.5kPa,再恒压缩至 体积为1dm3。求整个过程的W、Q、△U及△H。 解:n=1mol,理想气体 〔p=2026.5kPa 1=10dm3 要 y3=10dm3 V=ldm' W,=0 R2=-p4V=-P2(化-'2)=-2026.50-10 J(kPa-dm3) =[-2026.5×(-9 J(kPa-dm)=1824kJ W=形+形2=1824k灯 TEL:010-64434093
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 1 第二章 热力学第一定律习题及参考答案 1.5mol 理想气体于始态 1 t =25℃、 1 p =101.325kPa、V1 恒温膨胀至末态,已知末态体 积 2 1 V = 2V ,分别计算气体膨胀时反抗恒定外压 5 1 p(环) = 0. p 及进行可逆膨胀时系统所作 的功,并在 p-V 图上给出两种不同途径的功所对应的面积。 解: (1).反抗恒定外压 5 1 p(环) = 0. p 膨胀: 3 3 1 1 1 dm 122.3dm 101.325 5 8.314 298.15 ÷ = ø ö ç è æ ´ ´ = = p nRT V ( )( ) ( 0.5 101.325 122.32) 6.197kJ W1 = - p 环 V2 -V1 = - ´ ´ = - (2).可逆膨胀: J 8.59 J 2 ln 5 8.314 298.15ln 1 1 1 2 2 k V V V V W nRT = - ÷ ÷ ø ö ç ç è æ = - = - ´ ´ 2.1mol 理想气体由 202.66kPa、10dm3恒温升温,使压力升到 2026.5kPa,再恒压缩至 体积为 1dm3。求整个过程的W 、Q 、 DU 及 DH 。 解: n =1mol,理想气体 ï î ï í ì = = 1 3 1 1 10dm 202.65kPa T V p ï î ï í ì = = 2 3 2 2 10dm 2026.5kPa T V p ï î ï í ì = = 3 3 3 3 1dm 2026.5kPa T V p 0 W1 = ( ) [ 2026.5(1 10)](kPa dm ) 3 2 2 3 2 W = - pDV = - p V -V = - - × [ 2026.5 ( 9)](kPa dm ) 18.24kJ 3 = - ´ - × = 18.24kJ W = W1 +W2 = 理想气体 5mol 1 t =25℃ 1 p =101.325kPa V1 理想气体 5mol 2 t 2 p 2 1 V = 2V 恒容 W1 恒压 W2

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY rP乃=p,I=T 故△U=0,△H=0 0=-P=-182W 3.已知100℃、101.325kPa的恒温恒压下1mol水转变为水汽吸热40.64kJ。试求1mol 水由始态100℃、101.325kPa转变为同样温度、压力为40.53kPa的水汽末态时的△U及△H。 设水蒸气可视为理想气体,液体水的体积相对同样物质的量的水蒸气而言予忽略。 解:n=lmol H,00 (H,O(g) 40.53kPe 100C,K 100C,'3 100C △H,=Qp=40.64kJ △U=2+W=2。-p,(%2-)=Qp-p'2 =(40.64-1×8.314×373.15×10k=37.54k △H2=0,AU2=0 △U=△U1+AU2=37.54kJ 4.1mol理想气体于27℃、101.325kPa状态下受某恒定外压恒温压缩到平衡,再由该 状态下恒容升温至97℃,则压力升到1013.25kPa。求整个过程的W、Q、△U及△H。己 知该气体的C,恒定为20.92 J-.mol.K-. 解:n=lmol理想气体 [4=27TC 6=27C [3=97C (1) 10132P V=V, P库=A=A×号 W=-pgAV=-P:(V:-V)=-(p:V:-p:V) {-n会别 会别 千sm--m TEL:010-64434093 2
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 2 Q p3V3 = p1V1 ,T3 = T1 故 DU = 0 , DH = 0 Q = -W = -18.2kJ 3.已知 100℃、101.325kPa 的恒温恒压下 1mol 水转变为水汽吸热 40.64kJ。试求 1mol 水由始态 100℃、101.325kPa 转变为同样温度、压力为 40.53kPa 的水汽末态时的DU 及 DH 。 设水蒸气可视为理想气体,液体水的体积相对同样物质的量的水蒸气而言予忽略。 解: n = 1mol ï î ï í ì 1 2 100 C, 101.325kPa H O(l) V o ï î ï í ì 2 2 100 C , 101.325kPa H O(g) V o ï î ï í ì 100 C 40.53kPa H O(g) 2 o 40.64kJ DH1 = QP = 1 1 1 1 2 1 1 2 DU = Q +W = Qp - p (V -V ) = Qp - p V =(40.64-1×8.314×373.15×10-3)kJ=37.54kJ 0 DH2 = , 0 DU2 = 37.54kJ DU = DU1 + DU2 = 4.1mol 理想气体于 27℃、101.325kPa 状态下受某恒定外压恒温压缩到平衡,再由该 状态下恒容升温至 97℃,则压力升到 1013.25kPa。求整个过程的W 、Q 、DU 及 DH 。已 知该气体的Cv,m 恒定为 20.92 J×mol×K -1。 解: n = 1mol 理想气体 ï î ï í ì = = 1 1 1 101.325kPa 27 C V p t o ï î ï í ì = = 2 2 2 27 C V p p t 环 o ï î ï í ì = = = 3 2 3 3 1013.25kPa 97 C V V p t o 3 1 2 3 T T p环 = p = p ´ ( ) ( ) W1 = - p环DV = - p2 V2 -V1 = - p2V2 - p2V1 ú ú û ù ê ê ë é ÷ ÷ ø ö ç ç è æ = - - ´ ÷ ÷ ø ö ç ç è æ = - - 2 1 1 2 2 1 1 2 2 1 T T p p nRT p nRT nRT p ú ú û ù ê ê ë é ÷ ÷ ø ö ç ç è æ = - - ´ 3 1 1 3 2 1 T T p p nRT J 17740J 370.15 300.15 1 10 1 8.314 300.15 1 = ú û ù ê ë é ÷ ø ö ç è æ = - ´ ´ - ´ 恒容、恒压 (1) 恒温 (2) 恒容、恒外压 (1) 恒容 (2)

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY W2=0 W=W+W3=17740) △U=nC,2-1)=1×20.92(97-27J=1464J △H-nC.(43-41)=C,+R)13-41)-1×(8.314+20.92)×(97-27)-2046J Q=△U-W=(1464-17740)J=-16276J 5.已知78℃时乙醇的摩尔蒸发焓为39.47k1·mor,平衡压力为101.325kPa,平衡蒸 气体积为27.93dm3·mo'。若将20g78℃、101.325kPa的液体乙醇注入一真空容器中,蒸 发成蒸气后使容器中仍达到78℃及101.325kPa。求过程△H、△U、Q及W。 解:20g:CH,0H0 101.325kPa 101.325kPa 78℃ 78℃ 恒温、恒压② 向真空蒸发,W=0 △U=Q △U,△H状态函数,根据②过程计算: =A.=(需394u=1716 △U=O2+W3=△H-P%(W-)≈△H-P外 -7160-101352027937]p =(17160-1230J=15930J=15.9kJ Q=△U=15930J=15.9kJ 6.100℃,50.663kPa的水蒸气100dm等温可逆压缩至101.325kPa,并在101.325kPa 下继续压缩至10dmr为止。 ()试计算此过程的Q、W、△U、△H。已知100℃,101.325kPa,水的蒸发热4.06 ×10的·mo. (2)若使终态物系恒温100℃,反抗50.663kP外压,使其恢复到始态,求此过程中的Q、 W、△U、△H (3)若使终态物系恒温100℃向真空蒸发,并使其恢复至始态,求Q、W、△U、△H。 TEL:010-64434093
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 3 0 W2 = 17740J W = W1 +W2 = ( ) [1 20.92(97 27)]J 1464J DU = nCv t 2 - t 1 = ´ - = ( ) ( )( ) 1 (8.314 20.92) (97 27) 2046J DH = nCp t 3 - t 1 = n Cv + R t 3 - t 1 = ´ + ´ - = Q = DU -W = (1464 -17740)J = -16276J 5.已知 78℃时乙醇的摩尔蒸发焓为 39.47kJ·mol-1,平衡压力为 101.325kPa,平衡蒸 气体积为 27.93dm3·mol-1。若将 20g 78℃、101.325kPa 的液体乙醇注入一真空容器中,蒸 发成蒸气后使容器中仍达到 78℃及 101.325kPa。求过程 DH 、 DU 、Q 及W 。 解:20g:C2H5OH(l) C2H5OH(g) 101.325kPa 101.325kPa 78℃ 78℃ 向真空蒸发,W = 0 DU = Q DU , DH 状态函数,根据②过程计算: 39.47 (kJ) 17.16kJ 46 20 ÷ = ø ö ç è æ DH = nDvapHm = ´ 2 2 2 1 1 DU = Q +W = DH - p外 (V -V ) » DH - p外V 27.937 (J) 46 20 17160 101.325 ÷ ø ö ç è æ = - ´ ´ =(17160-1230)(J)=15930J=15.9kJ Q = DU = 15930J = 15.9kJ 6.100℃,50.663kPa 的水蒸气 100dm3 等温可逆压缩至 101.325kPa,并在 101.325kPa 下继续压缩至 10dm3为止。 (1) 试计算此过程的Q 、W 、DU 、DH 。已知 100℃,101.325kPa,水的蒸发热 4.06 ×104 J·mol-1。 (2) 若使终态物系恒温 100℃,反抗 50.663kPa 外压,使其恢复到始态,求此过程中的Q 、 W 、 DU 、 DH 。 (3) 若使终态物系恒温 100℃向真空蒸发,并使其恢复至始态,求Q 、W 、DU 、DH 。 真空蒸发 恒温① 恒温、恒压②

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 解: 100°C 等温可逆压缩 ,100℃ 可逆相变, 100C 101.325kPa△U 101.325kPa 10dm3 n(g) n(g) n(g) (1)△U1=0,△H,=0 g=-形=或ar=nrh片=nrh会=ph P. -[063x100 50.663=-3511J 101.325J 第一步下,n不变,对理想气体:P',=P h-o092h-0n 第二步是相变过程,冷凝成水的物质的量为: n=4-%=0-0-06m250=130m RT 8.314×373.15 △H2=-1.306×4.06×10J=-5.302×104J Q2=△H2=-5.302×10J W2=-p2△V=-[101.325×(10-50J=[40×101.325J=4052J △U2=02+W2=(-53020+4052)J=-48968J 所以得: △U=△U1+△U2=-48968J AH=△H.+AH、=-53020J Q=Q+02=(-3511-530201=-5653 W=(3511+4052J=75631 (2)此过程的始态与终态正好是(1)问中的始态与终态的颠倒,所以: △U=(U,-U,)=-(U3-U,)=48968J △H=(H1-H3)=-(H3-H,)=53020J W=-P4△V=-50.663100-10)J=-4559J TEL:010-64434093
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 4 解: ï ï î ï ï í ì ( ) 100dm 50.663kPa 100 C 1 3 n g o ï ï î ï ï í ì ( ) 101.325kPa 100 C 1 2 n g V o ï ï î ï ï í ì ( ) 10dm 101.325kPa 100 C 1 3 n g o (1) 0 DU1 = , 0 DH1 = 2 1 1 1 2 1 1 2 1 1 d ln ln ln 2 1 p p p V p p nRT V V Q W p V nRT V V = - = = = = ò J 3511J 101.325 50.663 50.663 100ln = - ú û ù ê ë é = ´ 第一步 T,n 不变,对理想气体: 2 2 1V1 p V = p 3 3 1 dm 50dm 101.325 100 50.663 = ú û ù ê ë é ´ V = 第二步是相变过程,冷凝成水的物质的量为: mol 1.306mol 8.314 373.15 1 1 2 2 50.66 100 101.325 10 1 2 = ´ ´ - ´ = - = - = RT p V RT p V n n n 1.306 4.06 10 J 5.302 10 J 4 4 DH2 = - ´ ´ = - ´ 5.302 10 J 4 Q2 = DH2 = - ´ [101.325 (10 50)]J [40 101.325]J 4052J W2 = - p2DV = - ´ - = ´ = ( 53020 4052)J -48968J DU2 = Q2 +W2 = - + = 所以得: 48968J DU = DU1 + DU2 = - 53020J DH = DH1 + DH2 = - ( 3511 53020)J 56531J Q = Q1 + Q2 = - - = - W = (3511+ 4052)J = 7563J (2) 此过程的始态与终态正好是(1) 问中的始态与终态的颠倒,所以: ( ) ( ) 48968J DU = U1 -U3 = - U3 -U1 = ( ) ( ) 53020J DH = H1 - H3 = - H3 - H1 = W = - p外DV = -50.663(100 -10)J = -4559J 等温可逆压缩 ΔU1 ΔH1 可逆相变 ΔU

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY Q=AU-W=(48968+45591=53527J (3)此过程的始态、终态与(2)问相同 ALJ=48968J △H=53020J W=-P%△V=0J Q=△U=48968J 7.64g02在101.325kPa,25℃时,绝热膨胀至50.663Pa,计算Q、W、△U,△H 已知:双原子分子Cm=3.5R,Cpm=2.5R. (1)若此过程可逆地进行: (2)若此过程是反抗恒定的50.663kPa外压的绝热膨胀。 解: 64g,02 64g,03 101.325kPa 绝热, 50.66kPa 25C 25R14 3.5R ()绝热可逆进行:Q=0,y= 护 ×298.15K=244.59K △U=nC(T2-T)= W-△U=-2226J △WH=AU+△(pr=△U+nRAT =[-2226+2×8.314×(244.59-298.15)]J=3117J (2)绝热不可逆膨胀; 0-0 △U=W nCr(G-7)=-P8(-V)=-Pa P:-P:) nRT:nRT TEL:010-64434093 5
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 5 Q = DU -W = (48968+ 4559)J = 53527J (3) 此过程的始态、终态与(2)问相同 DU = 48968J DH = 53020J W = - p外DV = 0J Q = DU = 48968J 7.64g O2在 101.325kPa,25℃时,绝热膨胀至 50.663kPa,计算Q 、W 、DU ,DH 。 已知:双原子分子Cp,m = 3.5R ,CV ,m = 2.5R 。 (1) 若此过程可逆地进行; (2) 若此过程是反抗恒定的 50.663kPa 外压的绝热膨胀。 解: ï î ï í ì 25 C 101.325kPa 64 ,O2 o g ï î ï í ì 2 2 50.66kPa 64 ,O T g (1) 绝热可逆进行:Q = 0 , 1.4 2.5 3.5 = = R R g g g 1 1 2 1 2 - ÷ ÷ ø ö ç ç è æ =÷ ÷ ø ö ç ç è æ r p p T T 298.15K 244.59K 101.325 50.663 1.4 1.4 1 2 ÷ ´ = ø ö ç è æ = - T 8.314 (244.59 298.15) J -2226J 2 5 32 64 ( ) 2 1 = ú û ù ê ë é DU = nCV T - T = ´ ´ ´ - W = DU = -2226J DH = DU + D( pV) = DU + nRDT =[-2226 + 2´8.314´ (244.59 - 298.15)]J = -3117J (2) 绝热不可逆膨胀: Q = 0 DU = W ÷ ÷ ø ö ç ç è æ - = - - = - - 1 1 2 2 2 1 2 1 ( ) ( ) p nRT p nRT nCV T T p外 V V p外 绝热
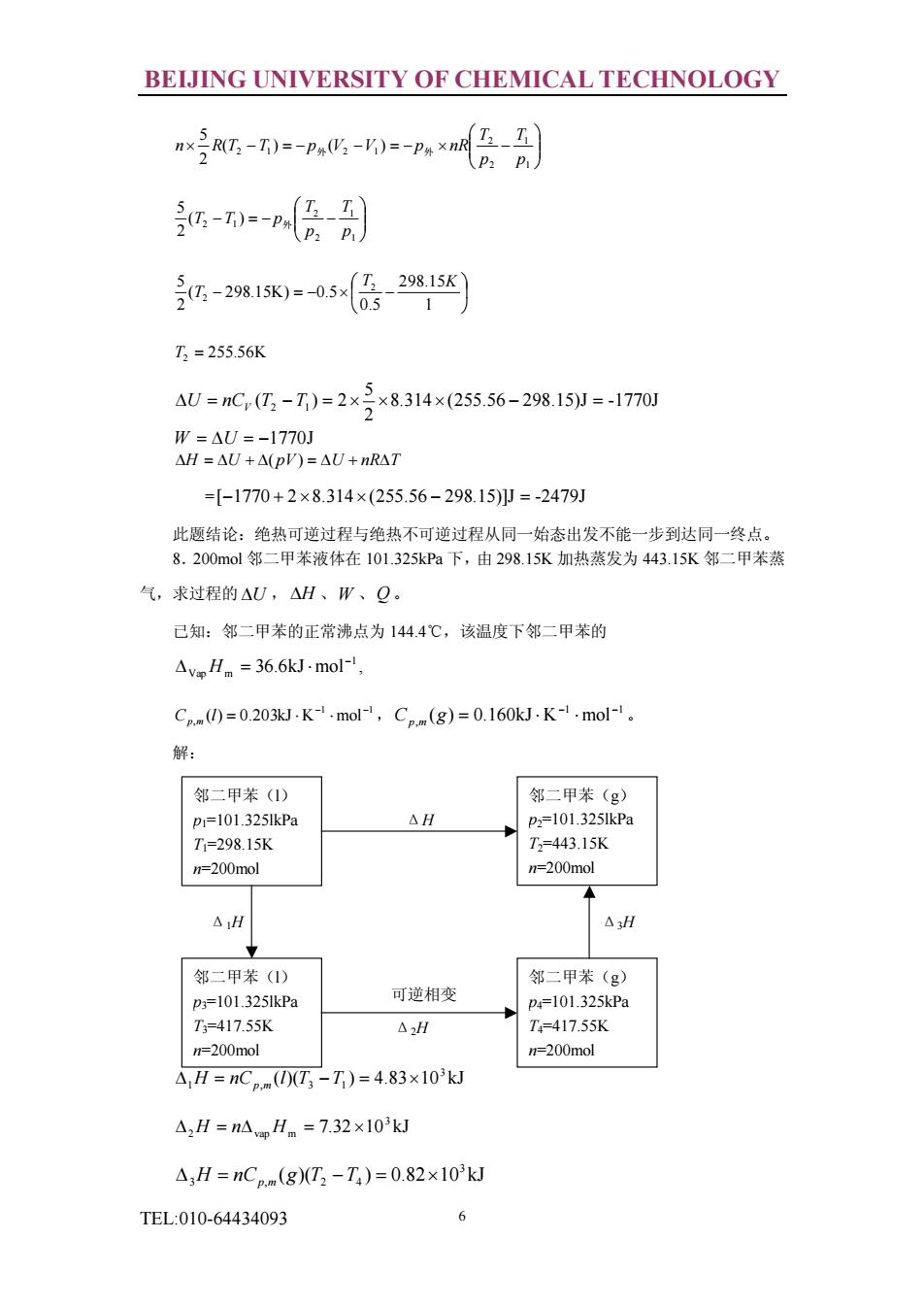
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY -,-0,很别 -层别 -281x=-05怎2%1 T=255.56K AW=mC,(G,-7)=2x3x8314x(25556-29815J=-170 =[-1770+2×8.314×(255.56-298.15p=-2479J 此题结论:绝热可逆过程与绝热不可逆过程从同一始态出发不能一步到达同一终点。 8.200mol邻二甲苯液体在101.325kPa下,由298.15K加热蒸发为443.15K邻二甲苯 气,求过程的△U,△H、W、Q 已知:邻二甲苯的正常沸点为144.4℃,该温度下邻二甲苯的 △vpHn=36.6 kJ-mol- C0=0.203k.K1,mol,Cpm(g)=0.160kJK-1.mol. 解: 邻二甲苯() 邻二甲苯(g) p1=101325IkPa △H D=101.325lkPa T=298.15K T=443.15K n=200mol △H △H 邻二甲苯() 邻二甲苯(g) g=101.325kP9 可逆相变 4=101.325kP T=417.55K △H T=417.55 =200mol =200m0l △H=nCp0T-T)=4.83×10kJ △,H=nApH。=7.32×103kJ △,H=nCpm(g)(T2-T)=0.82×103kJ TEL:010-64434093 6
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 6 ÷ ÷ ø ö ç ç è æ ´ - = - - = - ´ - 1 1 2 2 2 1 2 1 ( ) ( ) 2 5 p T p T n R T T p外 V V p外 nR ÷ ÷ ø ö ç ç è æ - = - - 1 1 2 2 2 1 ( ) 2 5 p T p T T T p外 ÷ ø ö ç è æ - = - ´ - 1 298.15 0.5 ( 298.15K) 0.5 2 5 2 2 T K T T2 = 255.56K 8.314 (255.56 298.15)J -1770J 2 5 ( ) 2 DU = nCV T2 - T1 = ´ ´ ´ - = W = DU = -1770J DH = DU + D( pV) = DU + nRDT =[-1770 + 2 ´8.314´ (255.56 - 298.15)]J = -2479J 此题结论:绝热可逆过程与绝热不可逆过程从同一始态出发不能一步到达同一终点。 8.200mol 邻二甲苯液体在 101.325kPa 下,由 298.15K 加热蒸发为 443.15K 邻二甲苯蒸 气,求过程的 DU , DH 、W 、Q 。 已知:邻二甲苯的正常沸点为 144.4℃,该温度下邻二甲苯的 1 Vap m 36.6kJ mol - D H = × , 1 1 , ( ) 0.203kJ K mol - - C l = × × p m , 1 1 , ( ) 0.160kJ K mol - - C g = × × p m 。 解: ( )( ) 4.83 10 kJ 3 D1H = nCp,m l T3 -T1 = ´ 7.32 10 kJ 3 D2H = nDvap H m = ´ ( )( ) 0.82 10 kJ 3 D3H = nCp,m g T2 -T4 = ´ 邻二甲苯(l) p1=101.325lkPa T1=298.15K n=200mol 邻二甲苯(g) p2=101.325lkPa T2=443.15K n=200mol 邻二甲苯(l) p3=101.325lkPa T3=417.55K n=200mol 邻二甲苯(g) p4=101.325kPa T4=417.55K n=200mol Δ1H Δ3H Δ2H ΔH 可逆相变

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY △H=△,H+△,H+△,H=12.97×103kJ Q=△H=12.97×103kJ 9.1mol某理想气体(Cm=20.0Jmol1.K-)由始态300K、200kPa分别经下列 恒温过程变化到终态压力为100kPa,求△U,△H、W和Q. (1)可逆膨胀。 (2)恒外压膨胀,外压等于终态压力: (3)向真空膨胀。 解:(1)对理想气体恒温过程有:△U-0,△H-0 理想气体恒温可逆膨胀: W-nR7nA=-1x8314×30n100 200=-1729J Q=-W=1729J (2)同(1)△U=0,△H=0 -134d-)-12 Q=-W=1247J (3)同(1)、(2)△U=0,△H=0 W=-p(环)W2-)=0J Q=-W=0J 10.在恒压下将2mol、0℃的冰加热,使之变成100℃的水蒸气。 已知:冰的4mH.(0°C)=6.02 kJ.mol,△pH.100C)=40.64kmol 液态水的C2m(0=75.3J-K-.mol, 求该过程的△U,△H、W和Q。 TEL:010-64434093
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 7 12.97 10 kJ 3 DH = D1H + D2H + D3H = ´ 12.97 10 kJ 3 Q = DH = ´ 9.1mol 某理想气体( 1 1 , 20.0J mol K - - = × × CV m )由始态 300K、200kPa 分别经下列 恒温过程变化到终态压力为 100kPa,求 DU , DH 、W 和Q 。 (1)可逆膨胀; (2)恒外压膨胀,外压等于终态压力; (3)向真空膨胀。 解:(1)对理想气体恒温过程有: DU = 0 , DH = 0 理想气体恒温可逆膨胀: J 1729J 100 200 ln 1 8.314 300ln 2 1 ÷ = - ø ö ç è æ = - = - ´ ´ p p W nRT Q = -W = 1729J (2)同(1) DU = 0 , DH = 0 ÷ ÷ ø ö ç ç è æ = - - ÷ ÷ ø ö ç ç è æ = - - = - - 1 2 2 1 ( )( 2 1 ) 2 1 p p nRT p nRT p nRT W p 环 V V p = J 1247J 200 100 1 8.314 300 1 = - ú û ù ê ë é ÷ ø ö ç è æ - ´ ´ - Q = -W = 1247J (3)同(1)、(2) DU = 0 , DH = 0 ( )( ) 0J W = - p 环 V2 -V1 = Q = -W = 0J 10.在恒压下将 2mol、0℃的冰加热,使之变成 100℃的水蒸气。 已知:冰的 1 fus m (0 C) 6.02kJ mol- D H = × o , 1 vap m (100 C) 40.64kJ mol- D H = × o 液态水的 1 1 , ( ) 75.3J K mol - - C l = × × p m , 求该过程的 DU , DH 、W 和Q
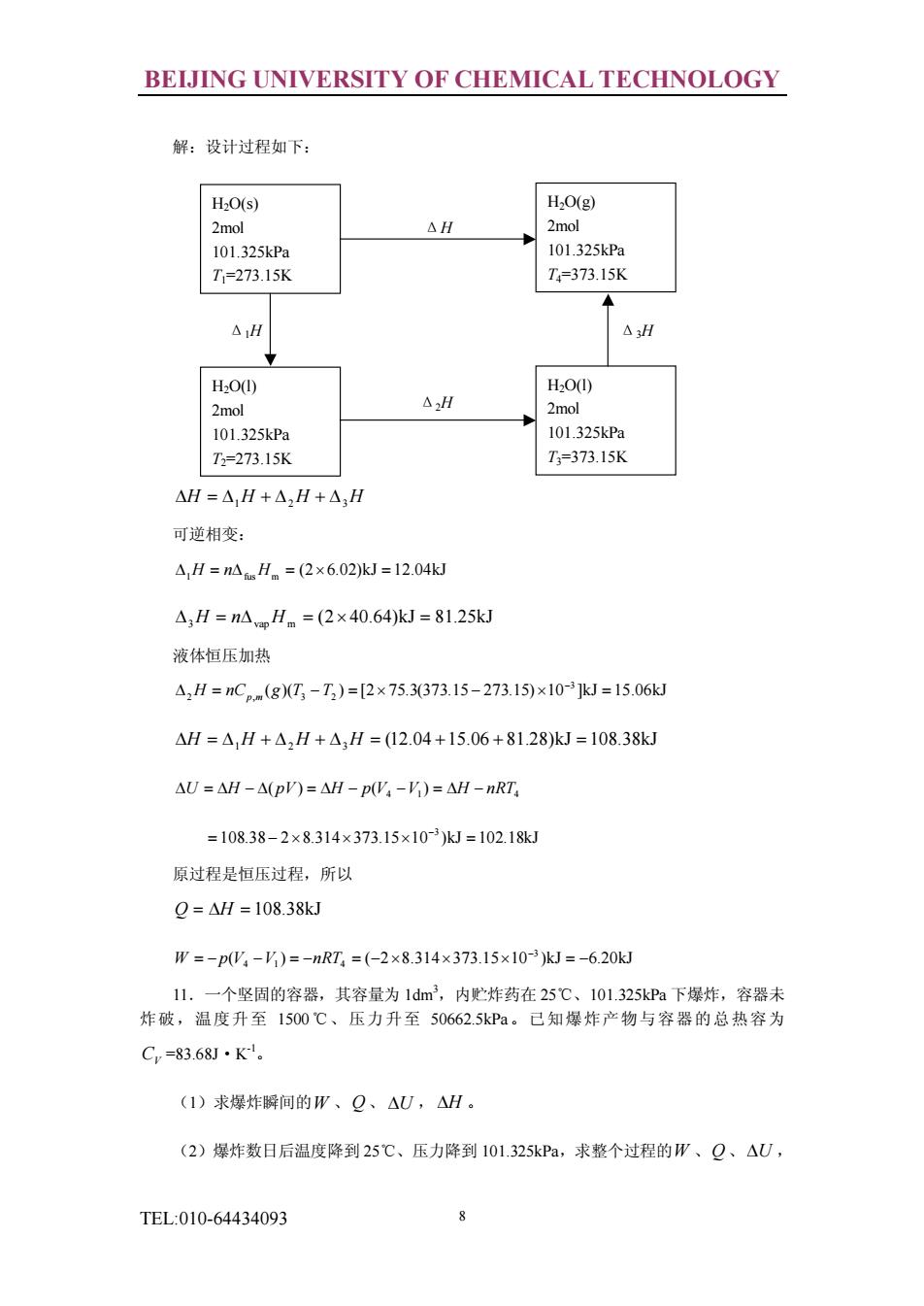
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY 解:设计过程如下: HO(s) H,0g) 2m0 △H 2mol 101.325kPa 101.325kP T-273.15K T=373.15K △H △H HO(I) H2O(D 2mol △,H 2mol 101.325kPa 101325kPa T=273.15K T=373.15K △H=△,H+△,H+△,H 可逆相变: A,H=nAH。=(2x6.02kJ=12.04W △H-nAH=(2×40.64)kJ-81.25kJ 液体恒压加热 △,H=nCp.(g(T,-T)=[2×75.3373.15-273.15)×10-3kJ=15.06J △H=△,H+△,H+△,H=12.04+15.06+81.28)kJ=108.38kJ △U=△H-△(p=△H-pW,-V)=H-nRT =108.38-2×8.314×373.15×10-3kJ=102.18k 原过程是恒压过程,所以 Q=H=108.38kJ W=-pW-)=-nRT=(-2x8.314×373.15x103k=-6.20 11.一个坚固的容器,其容量为1dm3,内贮炸药在25℃、101.325kP下爆炸,容器未 炸破,温度升至1500℃、压力升至50662.5kPa。已知爆炸产物与容器的总热容为 C=83.68J·K. (1)求爆炸瞬间的W、Q、△U,△H。 (2)爆炸数日后温度降到25℃、压力降到101.325kPa,求整个过程的W、Q、△U, TEL:010-64434093
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 8 解:设计过程如下: DH = D1H + D2H + D3H 可逆相变: (2 6.02)kJ 12.04kJ D1H = nDfusH m = ´ = (2 40.64)kJ 81.25kJ D3H = nDvapH m = ´ = 液体恒压加热 ( )( ) [2 75.3(373.15 273.15) 10 ]kJ 15.06kJ 3 D2 = , 3 - 2 = ´ - ´ = - H nCp m g T T (12.04 15.06 81.28)kJ 108.38kJ DH = D1H + D2H + D3H = + + = 4 1 4 DU = DH - D( pV) = DH - p(V -V ) = DH - nRT 108.38 2 8.314 373.15 10 )kJ 102.18kJ 3 = - ´ ´ ´ = - 原过程是恒压过程,所以 Q = DH = 108.38kJ ( ) ( 2 8.314 373.15 10 )kJ 6.20kJ 3 = - 4 - 1 = - 4 = - ´ ´ ´ = - - W p V V nRT 11.一个坚固的容器,其容量为 1dm3,内贮炸药在 25℃、101.325kPa 下爆炸,容器未 炸破,温度升至 1500℃、压力升至 50662.5kPa。已知爆炸产物与容器的总热容为 CV =83.68J·K -1。 (1)求爆炸瞬间的W 、Q 、 DU , DH 。 (2)爆炸数日后温度降到 25℃、压力降到 101.325kPa,求整个过程的W 、Q 、DU , H2O(s) 2mol 101.325kPa T1=273.15K Δ1H Δ3H Δ2H ΔH H2O(g) 2mol 101.325kPa T4=373.15K H2O(l) 2mol 101.325kPa T2=273.15K H2O(l) 2mol 101.325kPa T3=373.15K
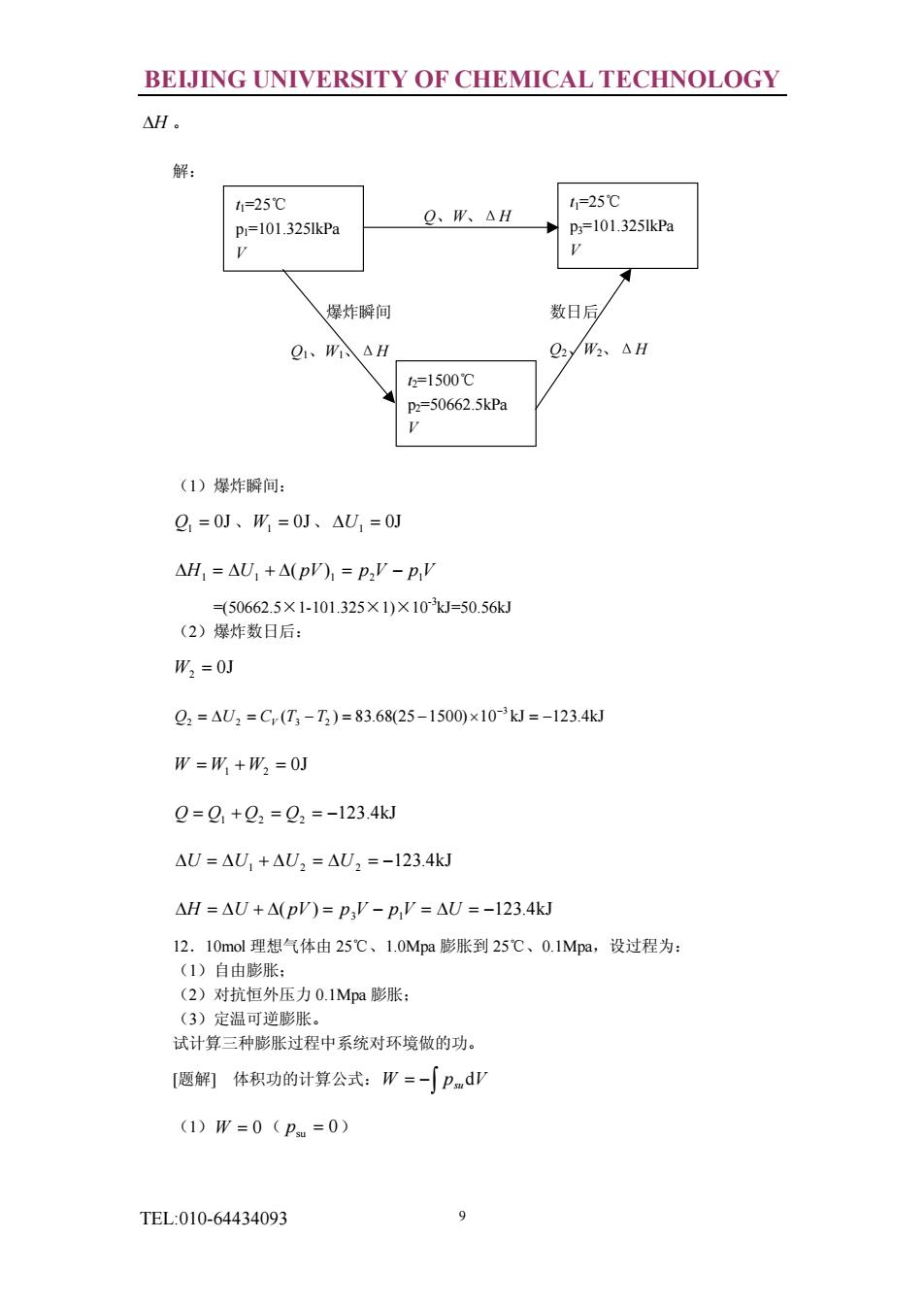
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY AH. 解: 1,=25℃ 1,=25℃ p=101.325kPa Q、W、△H p=101.325lkPa 爆炸瞬间 数日后局 Q、△ t=1500℃ 50662.5kPa (1)犀炸瞬间: g1=0J、W=0J、△U1=0J △H1=△U,+△(p),=P,'-p,V =50662.5×1-101.325×1)×10J-50.56k (2)爆炸数日后: W2=0J Q2=U2=C(T-)=83.68(25-1500)×103J=-123.4kJ W=用+W2=0J Q=Q,+02=Q2=-123.4kJ AU AU,+AU,AU2 =-123.4kJ △H=△U+△(pP)=P,'-p,'=△U=-123.4kJ 12.10mol理想气体由25C、1.0Mpa膨胀到25C、0.1Mpa,设过程为: ()自由膨胀 (2)对抗恒外压力0.,1Mp阳膨胀 (3)定温可逆膨胀。 试计算三种膨胀过程中系统对环境做的功。 [题解)体积功的计算公式:W=-∫PdV (1)W=0(Pm=0 TEL:010-64434093 9
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 9 DH 。 解: (1)爆炸瞬间: 0J Q1 = 、 0J W1 = 、 0J DU1 = DH1 = DU1 + D( pV) 1 = p2V - p1V =(50662.5×1-101.325×1)×10-3kJ=50.56kJ (2)爆炸数日后: 0J W2 = ( ) 83.68(25 1500) 10 kJ 123.4kJ 3 2 = D 2 = 3 - 2 = - ´ = - - Q U CV T T 0J W = W1 +W2 = 123.4kJ Q = Q1 + Q2 = Q2 = - 123.4kJ DU = DU1 + DU2 = DU2 = - ( ) 123.4kJ DH = DU + D pV = p3V - p1V = DU = - 12.10mol 理想气体由 25℃、1.0Mpa 膨胀到 25℃、0.1Mpa,设过程为: (1)自由膨胀; (2)对抗恒外压力 0.1Mpa 膨胀; (3)定温可逆膨胀。 试计算三种膨胀过程中系统对环境做的功。 [题解] 体积功的计算公式: ò W = - psu dV (1)W = 0 ( 0 psu = ) t1=25℃ p1=101.325lkPa V Q、W、ΔH t1=25℃ p3=101.325lkPa V t2=1500℃ p2=50662.5kPa V Q1、W1、ΔH Q2、W2、ΔH 爆炸瞬间 数日后

BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY (2)W=-P-AV--p.nRI1-L (PP2 =-0.1MPa×10mol×8.314J·mofr.K×298.15K×(1/0.1MPa-l/1.0MPa) -22.30kJ 3)P=-nRTn华】 =-57.05kJ [导引由计算结果可知,虽然三个过程的初态相同,终态也相同,但不同过程中的功 不相等。这是因为W不是状态函数,其值与过程有关。 13.298K时,将0.05kg的N2由0.1MPa定温可逆压缩到2MPa,试计算此过程的功. 如果被压缩了的气体在反抗外压力为0.1MPa下做定温膨胀再回到原来状态,问此过程的功 又是多少? [题解]n=50g28g·mor=1.79m 定温可逆压缩 2MPa =nRTIn =1.79molx.14]molxKIn IMPa-19k 若反抗外压力0.1MPa定温膨胀 成=ng贸 0.x10 Pax1.79mlx.4mo0.MPa2MPa 1 =-4.21kJ 用+W2≠0 导引]封闭系统由一个过程从始态(A)到达终态(B),再由另一个过程从终态(B) 回到 个始态(4),整个循环过程状态函数的改变量应为零 题中, 统经 两个不 同途径组成的循环过程由始态经过终态又回到始态,功的加和不为零,说明功是过程量,其 值与过程有关。 14.某理想气体,其Cvm=20小.K-,mol,现有该气体10mol处于283K,采取下 列不同途径升温至566K。试计算各个过程的W、Q、△U,△H并比较之 (1)体积保持不变: (2)系统与环境无热交换: (3)压力保持不变。 [题解(1)dV=0,W=0 ,=AU=nC.(T-T)=10mol×20J·K-l·molr'X(566-283)K=56.6k △H=nC.n(T2-T)=10mol×(20+8.314J·K·molr'×(566-283)K=80.129 TEL:010-64434093 6
BEIJING UNIVERSITY OF CHEMICAL TECHNOLOGY TEL:010-64434093 10 (2) ÷ ÷ ø ö ç ç è æ = - D = - - 1 2 su su 1 1 p p W p V p nRT =-0.1MPa×10mol×8.314J·mol-1·K -1×298.15K×(1/0.1MPa-1/1.0MPa) =-22.30kJ (3) ln ln 57.05kJ 1 2 1 2 = - ÷ ÷ ø ö ç ç è æ =÷ ÷ ø ö ç ç è æ = - p p nRT V V W nRT [导引] 由计算结果可知,虽然三个过程的初态相同,终态也相同,但不同过程中的功 不相等。这是因为W 不是状态函数,其值与过程有关。 13.298K 时,将 0.05kg 的 N2由 0.1MPa 定温可逆压缩到 2MPa,试计算此过程的功。 如果被压缩了的气体在反抗外压力为 0.1MPa 下做定温膨胀再回到原来状态,问此过程的功 又是多少? [题解] n =50g/28g·mol-1 =1.79mol 定温可逆压缩 13.29kJ 0.1MPa 2MPa ln 1.79mol 8.134J mol K 298Kln 1 1 1 2 1 = = ´ × × ´ = - - p p W nRT 若反抗外压力 0.1MPa 定温膨胀 ÷ ÷ ø ö ç ç è æ = - - = - - 2 2 1 su 2 2 su ' ( ' ) p nRT p nRT W p V V p ÷ ø ö ç è æ = - ´ ´ ´ × × ´ - - - 2MPa 1 0.1MPa 1 0.1 10 Pa 1.79mol 8.134J mol K 298K 6 1 1 = -4.21kJ 0 W1 +W2 ¹ [导引] 封闭系统由一个过程从始态(A)到达终态(B),再由另一个过程从终态(B) 回到同一个始态(A),整个循环过程状态函数的改变量应为零;本题中,系统经历两个不 同途径组成的循环过程由始态经过终态又回到始态,功的加和不为零,说明功是过程量,其 值与过程有关。 14.某理想气体,其 1 1 , 20J K mol - - = × × CV m ,现有该气体 10mol 处于 283K,采取下 列不同途径升温至 566K。试计算各个过程的W 、Q 、 DU , DH 并比较之。 (1)体积保持不变; (2)系统与环境无热交换; (3)压力保持不变。 [题解] (1)dV = 0,W = 0 ( ) QV = DU = nCV ,m T2 - T1 =10mol×20J·K -1·mol-1×(566-283)K=56.6kJ ( ) DH = nCp,m T2 -T1 =10mol×(20+8.314)J·K -1·mol-1×(566-283)K=80.129kJ