
第二章单一样本的推断问题 王星 明德主楼1019 wangxingwisdom@126.com
第二章 单一样本的推断问题 王 星 明德主楼1019 wangxingwisdom@126.com
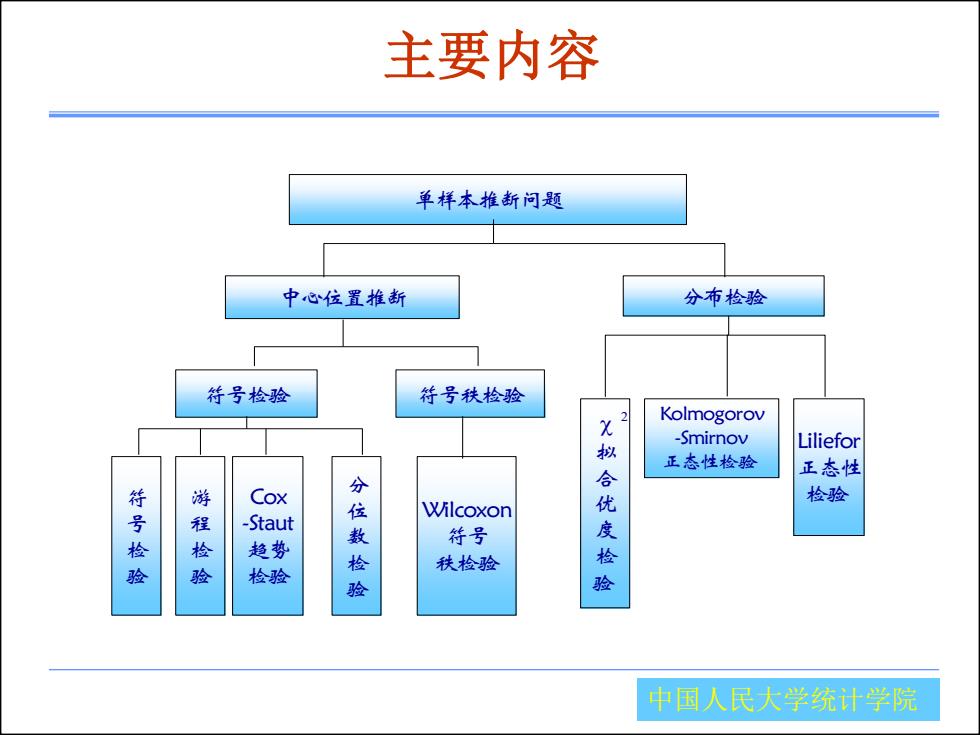
主要内容 单样本推断问题 中心位置推断 分布检验 符号检验 符号秩检验 2 X Kolmogorov -Smirnov Liliefor 正态性检验 正态性 COX 符号检 游程检 -Staut 分位 Wilcoxon 优 检验 特号 趋势 检 秩检验 检验 验 验 中国人民大学统计学院
中国人民大学统计学院 主要内容 符号检验 符号秩检验 分布检验 Wilcoxon 符号 秩检验 Kolmogorov -Smirnov 正态性检验 游 程 检 验 单样本推断问题 符 号 检 验 Liliefor 正态性 检验 拟 合 优 度 检 验 Cox -Staut 趋势 检验 2 中心位置推断 分 位 数 检 验

例1:假设某地16座预出售的楼盘均价,单位(百元/平方米)如表1所示: 表1.16座预出售的楼盘均价 363231 2528 36 40 32 412635 353287 33 35 问题:该地平均楼盘价格是否与媒体公布的3700元/平方米的说法相符? 依照题意,可以建立如下的零假设和备择假设: H0:4=37台H1:μ卡37 由于n=16<30为小样本,采用t检验计算检验统计量如下: t= X-0 S/W元 =-0.1412 根据自由度为n-1=16-1=15,得到t检验的p值为0.89,在显著性水平a<0.89 以下都不能拒绝零假设 中国人民大学统计学院
中国人民大学统计学院

第一节符号检验和分位数推断 假设总体FM,M是总体的中位数,对于假设检验问题: H0:M。=M→H:M≠M, M。是待检验的中位数取值 定义,s=∑1(x>M),s=21x<M,则s*+s=n,K=mins,s} 在零假设情况下K~b(n,0.5),在显著性水平为0的拒绝域为 Poinom(K<k|n',p=0.5)sa 其中k是满足上式最大的k值。 中国人民大学统计学院
中国人民大学统计学院 第一节 符号检验和分位数推断 假设总体 ,M是总体的中位数,对于假设检验问题: 是待检验的中位数取值 F(M) H : M M H : M M 0 e 0 1 e 0 M0 定义, , ,则 , 在零假设情况下 ,在显著性水平为 的拒绝域为 其中k是满足上式最大的k值。 n i 0 i 1 S I(x M ) n i 0 i 1 S I(x M ) ' s s n K min{s ,s } ' K ~ b(n ,0.5) ' P (K k | n ,p 0.5) binom

例3.1.假设某地16座预出售的楼盘均价,单位(百元/平方 米)如下表所示: 3632312528364032 4126353532873335 One-sample t-Test data:build.price-37 t=-0.1412,df=15,p-value= 0.8896 alternative hypothesis:true mean is not equal to 0 95 percent confidence interval: -8.0458537.045853 sample estimates: mean of x -0.5 中国人民大学统计学院
中国人民大学统计学院 例3.1. 假设某地16座预出售的楼盘均价,单位(百元/平方 米)如下表所示: 36 32 31 25 28 36 40 32 41 26 35 35 32 87 33 35 One-sample t-Test data: build.price - 37 t = -0.1412, df = 15, p-value = 0.8896 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: -8.045853 7.045853 sample estimates: mean of x -0.5

结果讨论 结论:符号检验在总体分布未知的情况下优于检验! 单边符号检验问题 H,:M≤M)H:M>M Poinom(S<kIn,p=0.5)sa H,:M.≥M,H1:M。<M,Pbinm(S<k|n,p=0.5)≤o k是满足式子的最大值 中国人民大学统计学院
中国人民大学统计学院 结果讨论 H : M M H : M M 0 e 0 1 e 0 ' P (S k | n ,p 0.5) binom k是满足式子的最大值 H : M M H : M M 0 e 0 1 e 0 ' P (S k | n ,p 0.5) binom 单边符号检验问题 结论:符号检验在总体分布未知的情况下优于t检验!

大样本结论 当n较大时 K9: K-n/ Vn/4 2→N0,1,n→0 当n不够大的时候可用修正公式进行调整。 双边:H,M。=MH,:M≠M,p-值2Po(ZM,D-值PNo.)(Z>z) 右侧:H,M.≥M,H:M.<M,,p-值Po(Z<Z) 中国人民大学统计学院
中国人民大学统计学院 大样本结论 当n较大时 : 当n不够大的时候可用修正公式进行调整。 双边: ,p-值 左侧: ,p-值 右侧: ,p-值 ' ' n n K ~ N( , ) 2 4 ' ' K n 2 Z N(0,1),n n 4 H : M M H : M M 0 e 0 1 e 0 2P (Z z) N(0,1) H : M M H : M M 0 e 0 1 e 0 H : M M H : M M 0 e 0 1 e 0 P (Z z) N(0,1) P (Z z) N(0,1)

课堂提问: 1.当n很大的时候,如何进行检验? 2.为什么要进行连续性修正? 3.在符号检验中如何进行连续性修正? 中国人民大学统计学院
中国人民大学统计学院 课堂提问: 1.当n很大的时候,如何进行检验? 2.为什么要进行连续性修正? 3.在符号检验中如何进行连续性修正? ?

符号检验在配对样本比较运用 配对样本(X1y1),(2y2),…(Xnyn) 将Xy1记为“x=y 记为“0”,记P为“+”比例,P.为“”比例, 那么假设检验问题: H:P=P.←→H1PP 可以用符号秩检验。 中国人民大学统计学院
中国人民大学统计学院 符号检验在配对样本比较运用 配对样本(x1 ,y1 ), (x2 ,y2 ) ,… (xn ,yn ) 将 记为“+”, 记为“-” , 记为“0” ,记P+ 为“+”比例, P- 为“-”比例, 那么假设检验问题: 可以用符号秩检验。 i i x y x y i i x y i i H0 :P+=P- H1 :P+=P-

1.符号检验应用举例 例32:设某化妆品厂商有A和B两个品牌,为了解客户对A品牌和B品 牌在使用上的差异,将A品牌和B品牌同时交给45个客户使用,一个月以 后得到以下数据: 喜欢A品牌的客户人数: 22人 喜欢B品牌的客户人数: 18人 不能区分的人数: 5人 解:假设检验问题: H0:P(A)=P(B)喜欢A品牌的客户和喜欢B品牌的客户比例相等 H1:P(A)卡P(B)喜欢A品牌的客户和喜欢B品牌的客户比例不等 中国人民大学统计学院
中国人民大学统计学院 1.符号检验应用举例