
应用回归分析 Applied Regression Analysis Applied 教材: Regression Analysis 何晓群,刘文卿: 《应用回归分析》第四版, 应用回归分析 (第四版) 中国人民大学出版社,2015年 何解刘文每编著 孔大网
应用回归分析 Applied Regression Analysis 教材: 何晓群,刘文卿: 《应用回归分析》第四版, 中国人民大学出版社,2015年

第1章回归分析概述 1.1变量间的统计关系 1.2回归方程与回归名称的由来 1.3回归分析的主要内容及其一般模型 1.4建立实际问题回归模型的过程 1.5回归分析应用与发展述评 思考与练习
第1章 回归分析概述 1 .1 变量间的统计关系 1 .2 回归方程与回归名称的由来 1 .3 回归分析的主要内容及其一般模型 1 .4 建立实际问题回归模型的过程 1 .5 回归分析应用与发展述评 思考与练习

1.1变量间的统计关系 函数关系 ■商品的销售额与销售量之间的关系 y=px 圆的面积与半径之间的关系 S=πR2 ■原材料消耗额与产量(x)、单位产量消耗(x2) 、原材料价格(x3)之间的关系 y=xx2x3
1 .1 变量间的统计关系 函数关系 商品的销售额与销售量之间的关系 y = px 圆的面积与半径之间的关系 S=R2 原材料消耗额与产量(x1 ) 、单位产量消耗(x2 ) 、原材料价格(x3 )之间的关系 y = x1 x2 x3
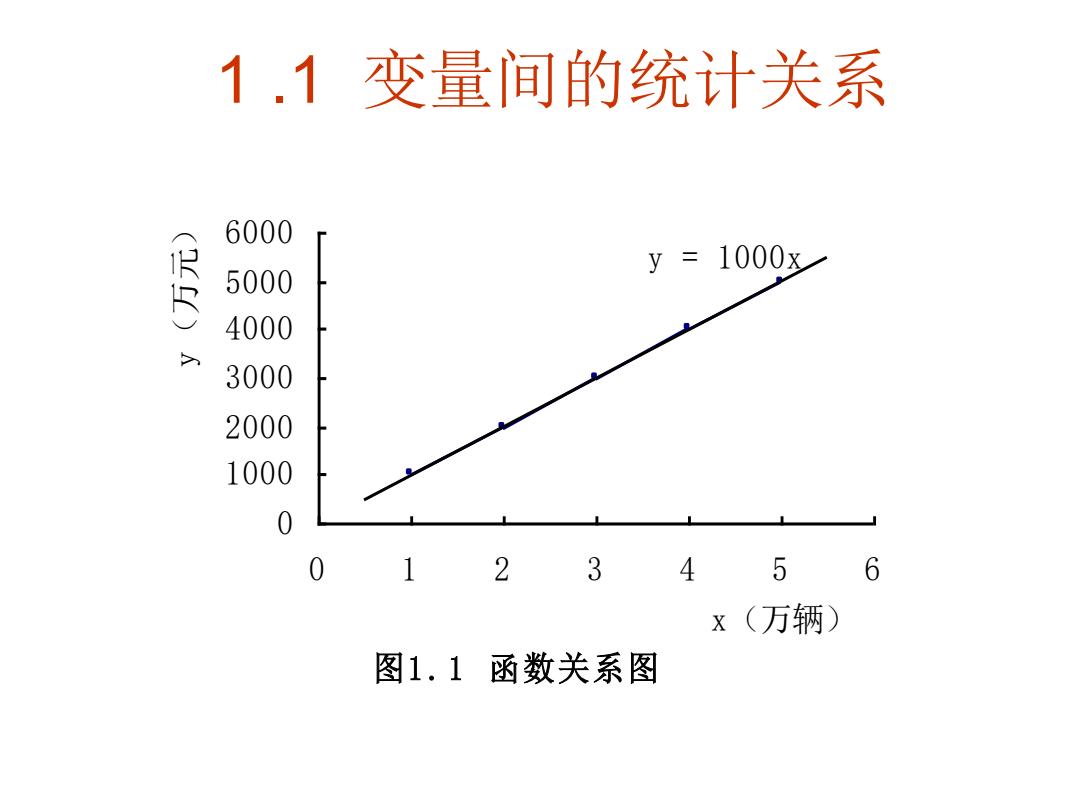
1.1变量间的统计关系 6000 y=1000x 5000 4000 3000 2000 1000 0 0 2 3 4 5 6 x(万辆) 图1.1函数关系图
1 .1 变量间的统计关系 图1 . 1 函数关系图 y = 1000x 0 1000 2000 3000 4000 5000 6000 0 1 2 3 4 5 6 x(万辆) y(万元)

1.1变量间的统计关系 相关关系的例子 子女身高y)与父亲身高(x)之间的关系 收入水平y)与受教育程度(x)之间的关系 ■粮食亩产量(y)与施肥量(x)、降雨量(x2)、温度(x3)之 间的关系 ■商品的消费量y)与居民收入(x)之间的关系 ■商品销售额y)与广告费支出(x)之间的关系
1 .1 变量间的统计关系 相关关系的例子 子女身高 (y)与父亲身高(x)之间的关系 收入水平(y)与受教育程度(x)之间的关系 粮食亩产量(y)与施肥量(x1 ) 、降雨量(x2 ) 、温度(x3 )之 间的关系 商品的消费量(y)与居民收入(x)之间的关系 商品销售额(y)与广告费支出(x)之间的关系
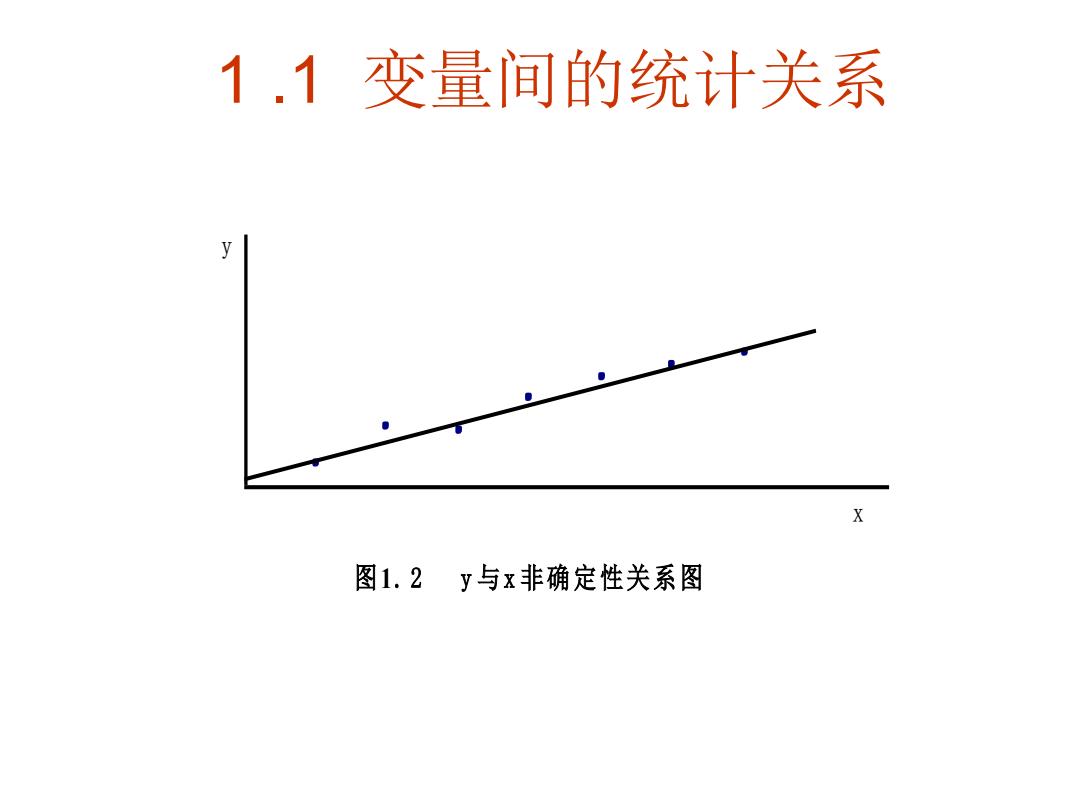
1.1变量间的统计关系 图1.2y与x非确定性关系图
1 .1 变量间的统计关系 图1. 2 y 与 x 非确定性关系图 x y
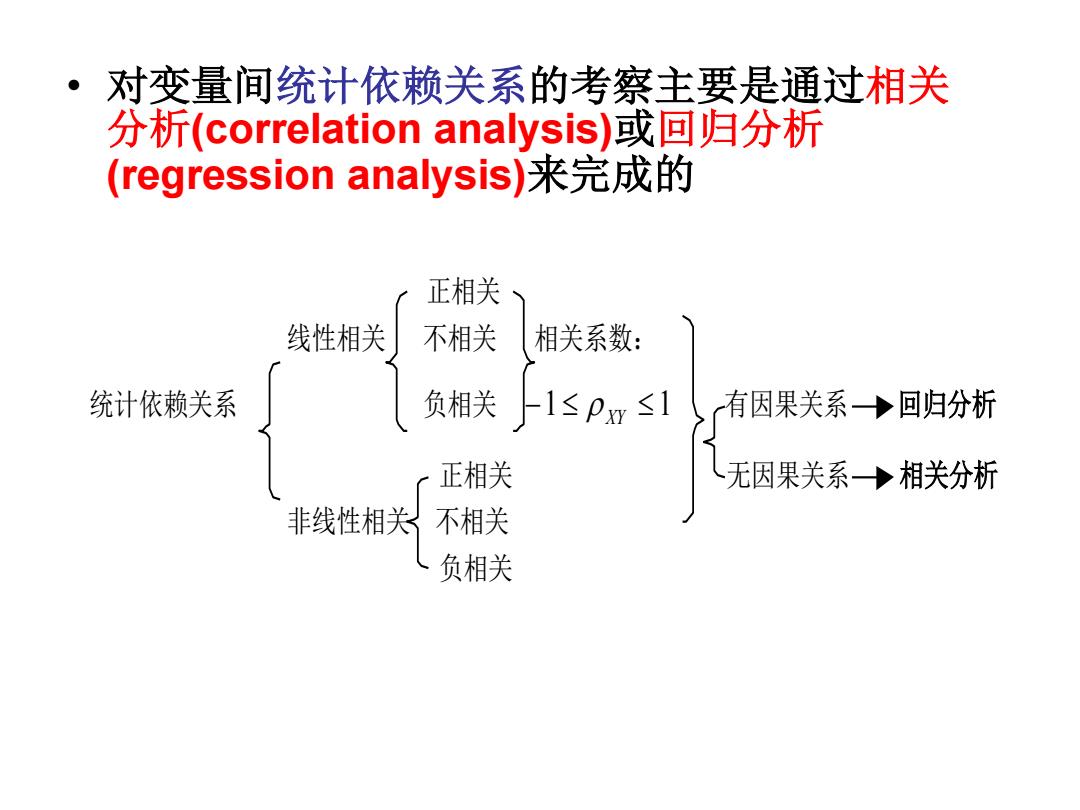
·对变量间统计依赖关系的考察主要是通过相关 分析(correlation analysis)或回归分析 (regression analysis)来完成的 正相关 线性相关 不相关 相关系数: 统计依赖关系 负相关上1≤pw≤1 有因果关系→回归分析 正相关 人无因果关系→相关分析 非线性相关不相关 (负相关
• 对变量间统计依赖关系的考察主要是通过相关 分析(correlation analysis)或回归分析 (regression analysis)来完成的 正相关 线性相关 不相关 相关系数: 统计依赖关系 负相关 1 1 XY 有因果关系 回归分析 正相关 无因果关系 相关分析 非线性相关 不相关 负相关

·注意 一①不线性相关并不意味着不相关。 ②有相关关系并不意味着一定有因果关系。 一③回归分析/相关分析研究一个变量对另一 个(些)变量的统计依赖关系,但它们并不 意味着一定有因果关系。 -④相关分析对称地对待任何(两个)变量, 两个变量都被看作是随机的。回归分析对变 量的处理方法存在不对称性,即区分应变量 (被解释变量)和自变量(解释变量):前 者是随机变量,后者不是
• 注意 – ①不线性相关并不意味着不相关。 – ②有相关关系并不意味着一定有因果关系。 – ③回归分析/相关分析研究一个变量对另一 个(些)变量的统计依赖关系,但它们并不 意味着一定有因果关系。 – ④相关分析对称地对待任何(两个)变量, 两个变量都被看作是随机的。回归分析对变 量的处理方法存在不对称性,即区分应变量 (被解释变量)和自变量(解释变量):前 者是随机变量,后者不是

。 回归分析构成计量经济学的方法论基础, 其主要内容包括: -(1)根据样本观察值对经济计量模型参数 进行估计,求得回归方程; 一(2)对回归方程、参数估计值进行显著性 检验; 一(3)利用回归方程进行分析、评价及预测
• 回归分析构成计量经济学的方法论基础, 其主要内容包括: – (1)根据样本观察值对经济计量模型参数 进行估计,求得回归方程; – (2)对回归方程、参数估计值进行显著性 检验; – (3)利用回归方程进行分析、评价及预测

1.2回归方程与回归名称的由来 英国统计学家F.Galton(1822-1911年)。 F.Galton和他的学生、现代统计学的奠基者之 K.Pearson(1856一1936年)在研究父母身高与其子女 身高的遗传问题时,观察了1078对夫妇, y=33.73+0.516x 成年儿子身高 父母平均身高
1 .2 回归方程与回归名称的由来 成年儿子身高 父母平均身高 英国统计学家F.Galton(1822-1911年)。 F.Galton和他的学生、现代统计学的奠基者之一 K.Pearson(1856—1936年)在研究父母身高与其子女 身高的遗传问题时,观察了1 078对夫妇, y ˆ 33.73 0.516x