
第2章一元线性回归 2.1一元线性回归模型 2.2参数B,、B1的估计 2.3最小二乘估计的性质 2.4回归方程的显著性检验 2.5残差分析 2.6回归系数的区间估计 2.7预测和控制 2.8本章小结与评注
第2章 一元线性回归 2 .1 一元线性回归模型 2 .2 参数β0、β1的估计 2 .3 最小二乘估计的性质 2 .4 回归方程的显著性检验 2 .5 残差分析 2 .6 回归系数的区间估计 2 .7 预测和控制 2 .8 本章小结与评注
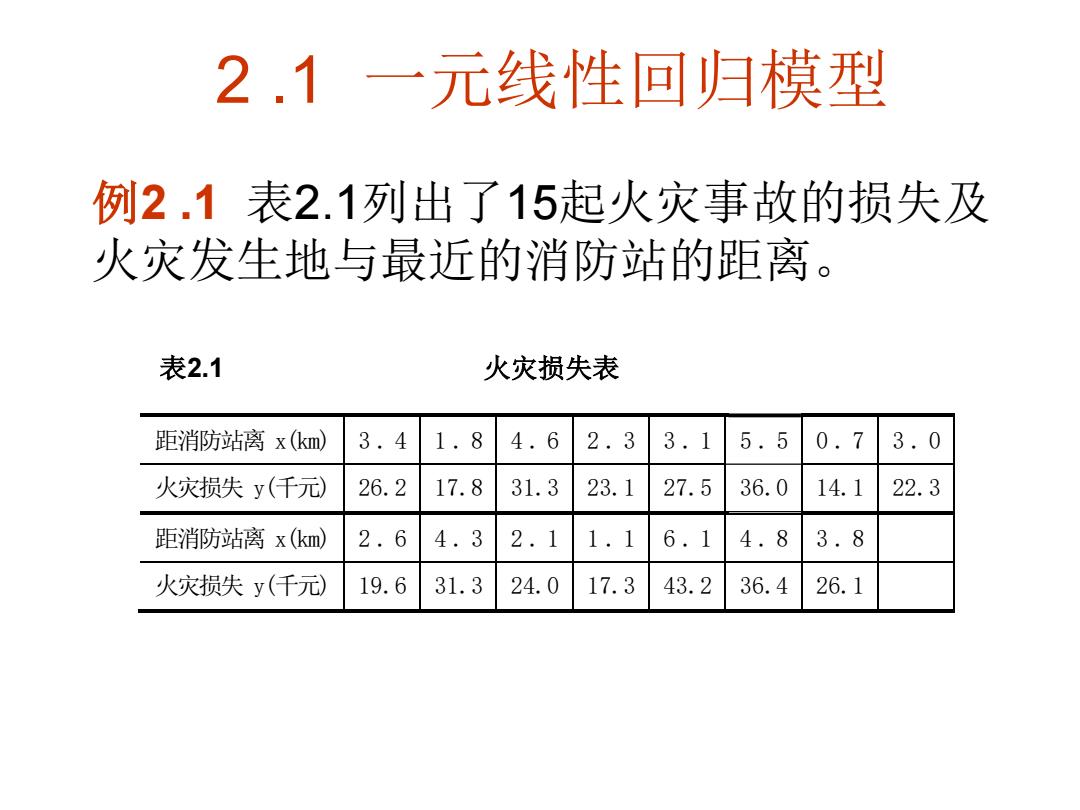
2.1一元线性回归模型 例2.1表2.1列出了15起火灾事故的损失及 火灾发生地与最近的消防站的距离。 表2.1 火灾损失表 距消防站离x(km) 3.4 1.8 4.62.33.15.50.73.0 火灾损失y(千元) 26.2 17.831.3 23.127.5 36.014.122.3 距消防站离x((km) 2.64.3 2.1 6. 4.83.8 火灾损失y(千元)19.631.324.017.343.2 36.426.1
2 .1 一元线性回归模型 例2 .1 表2.1列出了15起火灾事故的损失及 火灾发生地与最近的消防站的距离。 表2.1 火灾损失表 距消防站离 x(km) 3 . 4 1 . 8 4 . 6 2 . 3 3 . 1 5 . 5 0 . 7 3 . 0 火灾损失 y(千元) 26.2 17.8 31.3 23.1 27.5 36.0 14.1 22.3 距消防站离 x(km) 2 . 6 4 . 3 2 . 1 1 . 1 6 . 1 4 . 8 3 . 8 火灾损失 y(千元) 19.6 31.3 24.0 17.3 43.2 36.4 26.1
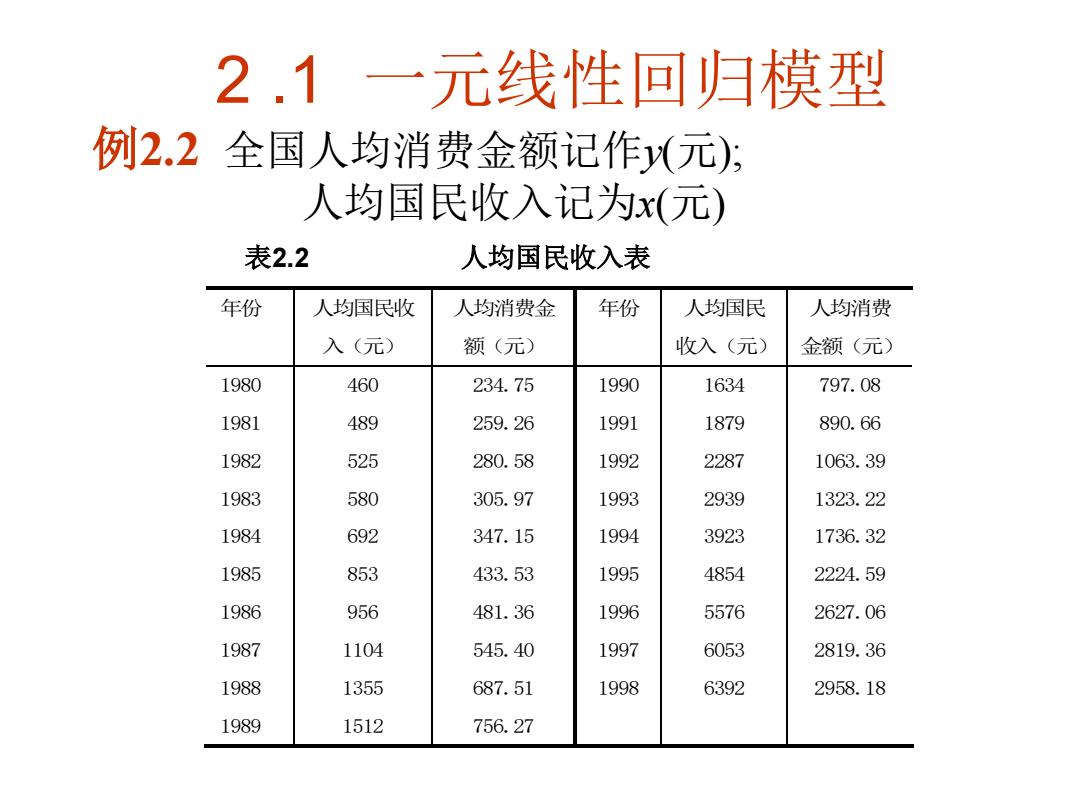
2.1一元线性回归模型 例2.2全国人均消费金额记作元); 人均国民收入记为x(元) 表2.2 人均国民收入表 年份 人均国民收 人均消费金 年份 人均国民 人均消费 入(元) 额(元) 收入(元) 金额(元) 1980 460 234.75 1990 1634 797.08 1981 259.26 1991 1879 890.66 19e2 525 280.58 1992 2287 1063.39 1988 305.97 1993 2939 1323.22 1984 692 347.15 1994 3923 1736.32 1985 853 433.53 1995 4854 2224.59 1986 956 481.36 1996 5576 2627.06 1987 1104 545.40 1997 6053 2819.36 1988 1355 687.51 1998 6392 2958.18 1989 1512 756.27
2 .1 一元线性回归模型 例2.2 全国人均消费金额记作y(元); 人均国民收入记为x(元) 表2.2 人均国民收入表 年份 人均国民收 入(元) 人均消费金 额(元) 年份 人均国民 收入(元) 人均消费 金额(元) 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 460 489 525 580 692 853 956 1104 1355 1512 234.75 259.26 280.58 305.97 347.15 433.53 481.36 545.40 687.51 756.27 1990 1991 1992 1993 1994 1995 1996 1997 1998 1634 1879 2287 2939 3923 4854 5576 6053 6392 797.08 890.66 1063.39 1323.22 1736.32 2224.59 2627.06 2819.36 2958.18

2.1一元线性回归模型 一元线性回归模型y=f+Bx+ε E(8)=0 var(s)=o2 回归方程E(yx)=$+Bx
2 .1 一元线性回归模型 一元线性回归模型 y=β0+β1 x+ε 2 var( ) ( ) 0 E 回归方程 E(y|x)=β0+β1x

2.1一元线性回归模型 样本观测值(x1y1),(x22),…,(xnyn) 样本模型y=o+βx+e =1,2,…,n E(s)=0 i=1,2,…,n var(s)=o2 回归方程E0y,)-+βx,Var0y,)=o2, 经验回归方程=B。+Bx
2 .1 一元线性回归模型 样本模型 yi =β0+β1 xi+εi , i=1,2,…,n 回归方程 E(yi )=β0+β1 xi ,var(yi )=σ2 , 样本观测值(x1 ,y1 ),(x2 ,y2 ),…,(xn ,yn ) i , , ,n E i i 1 2 var( ) ( ) 0 2 经验回归方程 y x 0 1 ˆ ˆ ˆ

2.2参数Bo、B的估计 一、普通最小二乘估计 (Ordinary Least Square Estimation,简记为OLSE) 最小二乘法就是寻找参数B。、B,的估计值使离差平方和达极小 Q(B。,月)=之(y-B。-Bx)尸 =min2oy-B。-Bx,)2 B,B )=B。+户,x,称为y的回归拟合值,简称回归值或拟合值 e,=y-少 称为y的残差
2 .2 参数β0、β1的估计 一、普通最小二乘估计 (Ordinary Least Square Estimation,简记为OLSE) n i i i n i i i y x Q y x 1 2 0 1 , 1 2 0 1 0 1 min ( ) ) ˆ ˆ ) ( ˆ , ˆ ( 0 1 最小二乘法就是寻找参数β0、β1的估计值使离差平方和达极小 i i y x 0 1 ˆ ˆ ˆ i i i e y y ˆ 称为yi的回归拟合值,简称回归值或拟合值 称为yi的残差
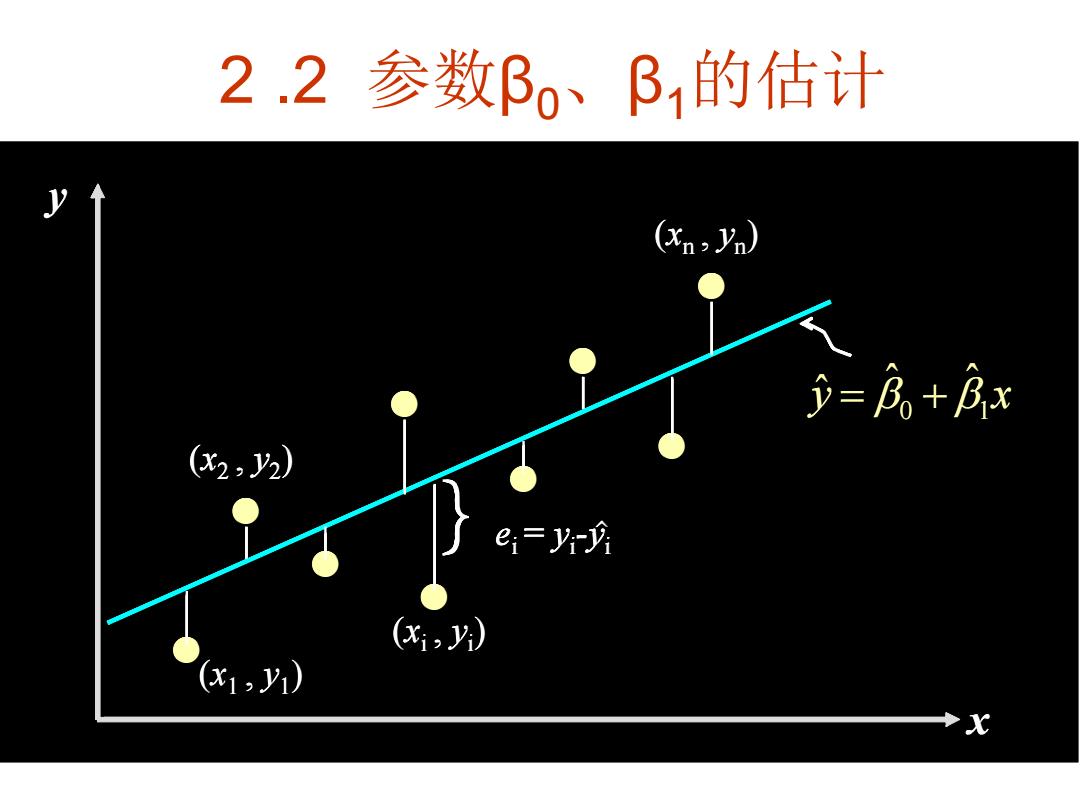
2.2参数B、B的估计 y (n>yn) ● =Bo+Bx (x2,2) ei=yi-y (x,y) (x1,y1)
2 .2 参数β0、β1的估计 x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i y x 0 1 ˆ ˆ yˆ x 0 1 ˆ ˆ ˆ x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i y x 0 1 ˆ ˆ yˆ x 0 1 ˆ ˆ ˆ x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i x y (xn , yn ) (x1 , y1 ) (x 2 , y2 ) (xi , yi ) }ei = yi -y^i (x 2 , y2 ) (xi , yi ) }ei = yi -y^i ei = yi -y^i y x 0 1 ˆ ˆ yˆ x 0 1 ˆ ˆ ˆ

2.2参数Bo、B1的估计 服R=A=-20-A-x)=0 8 含=0 A=A-22y-月-月x=0 80 经整理后,得正规方程组 哦+(区月=立y ②成+2a-2
2 .2 参数β0、β1的估计 ) 0 ˆ ˆ 2 ( ˆ ) 0 ˆ ˆ 2 ( ˆ 1 0 1 1 1 1 1 0 1 0 0 0 n i i i i n i i i y x x Q y x Q 经整理后,得正规方程组 n i n i n i i i i i n i i n i i x x x y n x y 1 1 1 1 2 0 1 1 1 0 ˆ ( ) ˆ ( ) ˆ ( ) ˆ 0 0 1 1 n i i i n i i x e e

2.2参数Bo、B1的估计 B。=少-月x 得OLSE为 2a-w西 26-列 人-立-2-m时 记 ,2-Wg-n-交-n时 B。=-Bx B.=Lg/La
2 .2 参数β0、β1的估计 2 1 1 1 0 1 ( ) ( )( ) ˆ ˆ ˆ n i i i n i i x x x x y y y x 得OLSE 为 n i n i xx i i L x x x n x 1 1 2 2 2 ( ) ( ) n i i i n i xy i i L x x y y x y nx y 1 1 ( )( ) Lxy Lxx y x / ˆ ˆ ˆ 1 0 1 记

2.2参数Bo、B的估计 续例2.1 x=492-328,D=3962=26415 15 15 Lo=x-) =196.16-15(3.28)2=34.784 L=∑y-nx万 =1470.65-1299.536=171.114 [B,=-Bx=26.413-4.919×3.28=10.279 B=L,/L=171.114/34.784=4.919 )=10.279+4.919x 回归方程
2 .2 参数β0、β1的估计 26.413 15 396.2 3.28 , 15 49.2 x y 196.16 15(3.28) 34.784 ( ) 2 1 2 2 n i xx i L x n x 1470.65 1299.536 171.114 1 n i xy i i L x y n x y / 171.114/ 34.784 4.919 ˆ 26.413 4.919 3.28 10.279 ˆ ˆ 1 0 1 Lxy Lxx y x y ˆ 10.279 4.919x 续例2.1 回归方程