
第四章违背基本假设的情况 4.1异方差性产生的背景和原因 4.2一元加权最小二乘估计 4.3多元加权最小二乘估计 4.4自相关性问题及其处理 4.5异常值与强影响点 4.6本章小结与评注
第四章 违背基本假设的情况 4.1 异方差性产生的背景和原因 4.2 一元加权最小二乘估计 4.3 多元加权最小二乘估计 4.4 自相关性问题及其处理 4.5 异常值与强影响点 4.6 本章小结与评注

第四章违背基本假设的情况 Gauss-Markov条件 E(e)=0,i=1,2,…,n coge,)=a3,1=/ (ij=1,2,…,n 0,i≠
第四章 违背基本假设的情况 ( 1, 2, , ) ( ) ( ) 1, 2, , i ,j n 0 , i j σ , i j cov ε ,ε E ε 0, i n 2 i j i Gauss-Markov条件

4.1异方差性产生的背景和原因 一、异方差产生的原因 例4.1居民收入与消费水平有着密切的关系。用x 表示第i户的收入量,y;表示第i户的消费额,一个简单的 消费模型为: yFβo+B1xte,iF1,2,…,n 低收入的家庭购买差异性比较小, 高收入的家庭购买行为差异就很大。 导致消费模型的随机项ε:具有不同的方差
4.1 异方差性产生的背景和原因 一、异方差产生的原因 例4.1 居民收入与消费水平有着密切的关系。用xi 表示第i户的收入量,yi表示第i户的消费额,一个简单的 消费模型为: yi=β0+β1 xi+εi ,i=1,2,…,n 低收入的家庭购买差异性比较小, 高收入的家庭购买行为差异就很大。 导致消费模型的随机项εi具有不同的方差

4.1异方差性产生的背景和原因 二、异方差性带来的问题 当存在异方差时,普通最小二乘估计存在以下问题: ()参数估计值虽是无偏的,但不是最小方差线性无偏估计: (2)参数的显著性检验失效: (3)回归方程的应用效果极不理想
4.1 异方差性产生的背景和原因 二、异方差性带来的问题 当存在异方差时,普通最小二乘估计存在以下问题: (1)参数估计值虽是无偏的,但不是最小方差线性无偏估计; (2)参数的显著性检验失效; (3)回归方程的应用效果极不理想

4.2一元加权最小二乘估计 一、异方差性的检验 (一)残差图分析法 图2.5(b) 存在异方差 (b)
4.2 一元加权最小二乘估计 一、异方差性的检验 (一)残差图分析法 (b) x e 0 图2.5(b) 存在异方差

4.2一元加权最小二乘估计 一、异方差性的检验 (二)等级相关系数法 等级相关系数检验法又称斯皮尔曼(Spearman)检验,是一 种应用较广泛的方法。这种检验方法既可用于大样本,也可 用于小样本。进行等级相关系数检验通常有三个步骤。 第一步,作关于x的普通最小二乘回归,求出ε的估计值 即e,的值
4.2 一元加权最小二乘估计 一、异方差性的检验 (二)等级相关系数法 等级相关系数检验法又称斯皮尔曼(Spearman)检验,是一 种应用较广泛的方法。这种检验方法既可用于大样本,也可 用于小样本。进行等级相关系数检验通常有三个步骤。 第一步,作y关于x的普通最小二乘回归,求出ei的估计值, 即ei的值

4.2一元加权最小二乘估计 (二)等级相关系数法 第二步,取e,的绝对值,分别把x和e按递增(或 递减)的次序分成等级,按下式计算出等级相关 系数: -1- 6 nn2-1)台 其中,n为样本容量,d为对应于x和le的等级的差数
4.2 一元加权最小二乘估计 (二)等级相关系数法 第二步,取ei的绝对值,分别把xi和|ei |按递增(或 递减)的次序分成等级,按下式计算出等级相关 系数: n i s di n n r 1 2 2 ( 1) 6 1 其中,n为样本容量,di为对应于xi和|ei |的等级的差数

4.2一元加权最小二乘估计 (二)等级相关系数法 第三步,做等级相关系数的显著性检验。在n>8的情况下, 用下式对样本等级相关系数,进行检验。检验统计量为: n-2 r f= V1- 如果t2(n-2)可认为异方差性问题不存在, 如果t>tw2(n-2),说明x与e,之间存在系统关系,异方差性 问题存在
4.2 一元加权最小二乘估计 (二)等级相关系数法 第三步,做等级相关系数的显著性检验。在n>8的情况下, 用下式对样本等级相关系数rs进行t检验。检验统计量为: 如果t≤tα/2(n-2)可认为异方差性问题不存在, 如果t>tα/2(n-2),说明xi与|ei |之间存在系统关系,异方差性 问题存在。 2 1 2 s s r n r t
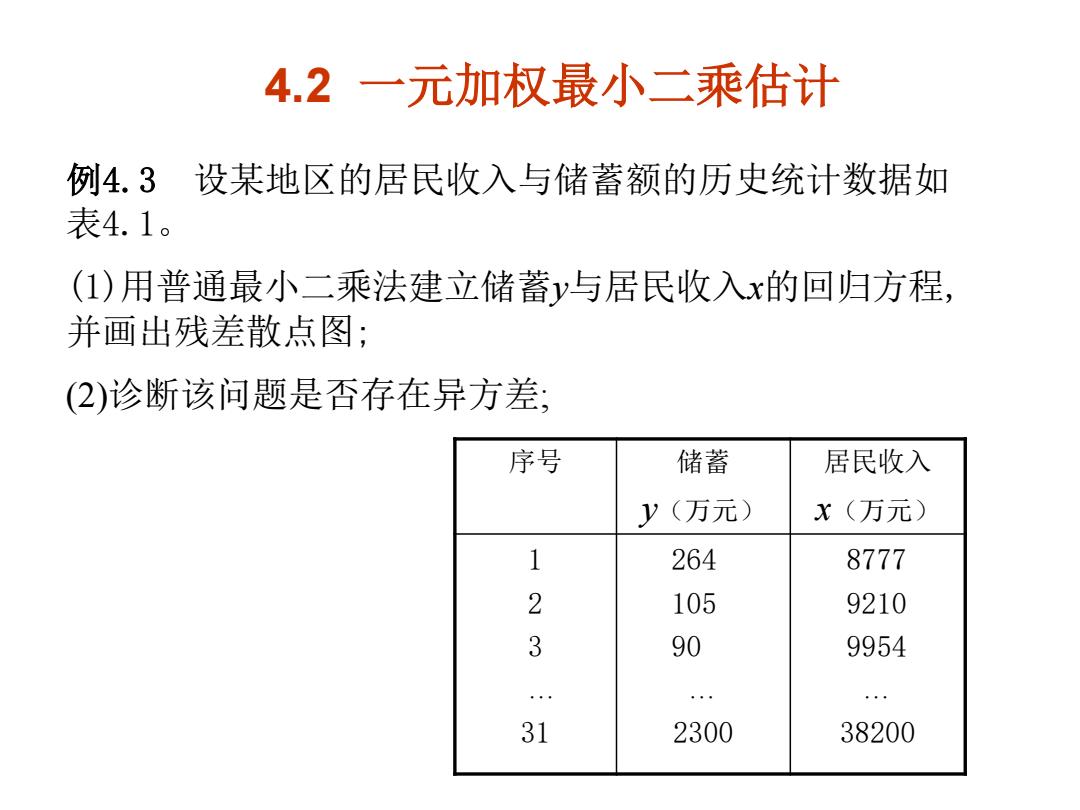
4.2一元加权最小二乘估计 例4.3设某地区的居民收入与储蓄额的历史统计数据如 表4.1。 (1)用普通最小二乘法建立储蓄y与居民收入x的回归方程, 并画出残差散点图; (2)诊断该问题是否存在异方差; 序号 储蓄 居民收入 y(万元) x(万元) 1 264 8777 2 105 9210 3 90 9954 … … 31 2300 38200
4.2 一元加权最小二乘估计 例4.3 设某地区的居民收入与储蓄额的历史统计数据如 表4.1 (1)用普通最小二乘法建立储蓄y与居民收入x的回归方程, 并画出残差散点图; (2)诊断该问题是否存在异方差; 序号 储蓄 y(万元) 居民收入 x(万元) 1 2 3 … 31 264 105 90 … 2300 8777 9210 9954 … 38200

4.2一元加权最小二乘估计 序号 储蓄y 居民收入x x等级 残差e, le le等级 d d 1 264 8777 169.0 169.0 16 -15 225 105 9210 2 -26.6 26.6 3 1 90 9954 -104.6 104.6 7 4 16 131 10508 -110.5 110.5 8 -4 16 5 122 10979 -159.4 159.4 15 -10 100 6 107 11912 6 -253.4 253.4 23 -17 289 7 406 12747 > -25.1 25.1 2 5 25 8 503 13499 8.2 82 1 7 49 9 431 14269 9 -129.0 129.0 9 0 0 10 588 15522 -78.0 78.0 4 6 36 16730 129.7 129.7 10 1 1 12 950 17663 12 102.7 102.7 6 6 36 13 79 18575 6 -145.5 145.5 -1 1 14 819 19635 14 195.3 195.3 19 -5 25 15 1222 21163 15 78.4 784 5 10 100 31 2300 38200 31 -286.1 286.1 24 7 49
4.2 一元加权最小二乘估计 序号 储蓄y 居民收入x xi等级 残差ei |ei | |ei |等级 di 1 264 8777 1 169.0 169.0 16 -15 225 2 105 9210 2 -26.6 26.6 3 -1 1 3 90 9954 3 -104.6 104.6 7 -4 16 4 131 10508 4 -110.5 110.5 8 -4 16 5 122 10979 5 -159.4 159.4 15 -10 100 6 107 11912 6 -253.4 253.4 23 -17 289 7 406 12747 7 -25.1 25.1 2 5 25 8 503 13499 8 8.2 8.2 1 7 49 9 431 14269 9 -129.0 129.0 9 0 0 10 588 15522 10 -78.0 78.0 4 6 36 11 898 16730 11 129.7 129.7 10 1 1 12 950 17663 12 102.7 102.7 6 6 36 13 779 18575 13 -145.5 145.5 14 -1 1 14 819 19635 14 -195.3 195.3 19 -5 25 15 1222 21163 15 78.4 78.4 5 10 100 … … … … … … … … … 31 2300 38200 31 -286.1 286.1 24 7 49 2 di