石河子大学：《通信原理》课程教学资源（实验指导）通信原理仿真实验指导－MATLAB版

通信原理仿真实验指导 一MATLAB版 编辑：田敏、李新弘、查志华 信息科学与技术学院现代通信教研室

通信原理仿真实验指导 －MATLAB 版 编辑：田敏、李新弘、查志华 信息科学与技术学院现代通信教研室

教材使用说明 本教材由三部分组成。第一部分是实验中应当遵循的详尽的实验向导：第二部分包括 实验内容、预习作业和课后作业：第三部分是附录。附录A为大家概述了仿真环境的一些 基本假设，通过仔细地阅读附录A将有助于对仿真环境比较深刻的理解：附录B简明地列出 了诵信系统工具句中的MAΠAB函傲清单。 完成本教材中的实验，你无须预先掌握任何关于MATLAB软件的知识，从某种意义上说 任何人都可以根据操作向导轻松地完成实验。如果你想完成本教材所包含内容以外的实 验，MATLAB在线帮助功能通常能够满足你的要求，使你得心应手。 在做每一个实哈之前，首先应当完成预习作业。这些问颗是从与特定实验相关的原材 中提取出来的。其目的是让同学们有所准备，以便在实验中对基本概念理解得更加深刻

―V― 教材使用说明 本教材由三部分组成。第一部分是实验中应当遵循的详尽的实验向导；第二部分包括 实验内容、预习作业和课后作业；第三部分是附录。附录 A 为大家概述了仿真环境的一些 基本假设,通过仔细地阅读附录 A 将有助于对仿真环境比较深刻的理解；附录 B 简明地列出 了通信系统工具包中的 MATLAB 函数清单。 完成本教材中的实验,你无须预先掌握任何关于 MATLAB软件的知识,从某种意义上说, 任何人都可以根据操作向导轻松地完成实验。如果你想完成本教材所包含内容以外的实 验,MATLAB 在线帮助功能通常能够满足你的要求,使你得心应手。 在做每一个实验之前,首先应当完成预习作业。这些问题是从与特定实验相关的原材料 中提取出来的。其目的是让同学们有所准备,以便在实验中对基本概念理解得更加深刻

字体和印刷约定 本教材的一些习惯用法： ●斜体字用来表示它是MATLAB函数名，有时也表示强调，例如： 利用MATLAB函数gaus pdf和gaus cdf显示随机变量的概率密度函数和分布函数。 ●“>》”符号是MATLAB的提示符，运行MATLAB后在你的终端上会出现此符号。有时 则由于MATLAB版本或设置的不同，在MATLAB的命令窗口中并没有此符号，但这 些都不会影响实验过程。 ●文本中的铅字（粗体字）表示它们是从MATLAB命令窗口得到的变量。你可以直接 调用其值进行计算。例如计算随机序列abc的均值和方差 >mean_abc mean(abc):var_abc var(abc): 其中mean_abc和var_abc分别代表abc的均值和方差 ●出现在文本行中首字母大写的单词是你应键入的命令。例如： 如果ee_diag函数的第二个参数是负的，要显示下一个轨迹请敲击“Enter”键，这里的 “Enter'”就是你必须键入的命令。 ●出现在黑线框中的问题是课后作业，这些问题必须以书面形式完成并在做下一次实 验之前交给指导教师。最后实验成绩评定时也要以此为参考。例如： 问题12如果分布率是基于2000次实验的结果，计算每面发生的次数。 ●为了实现在通信系统工具包(Communication System Toolbox)内部的通信，大量的 MATLAB全局变量是必不可少的。MATLAB的staI函数会为每一个实验中所用全 局变量赋以必要的初值。进入MATLAB工作站进行实验的第一步，你必须首先执行下 面的命令： >start 之后，你会得到一个友好的界面，它会给你提供一些其它信息。 请切记： ●安装MATLAB时，请安装"Signal Processing”库 ●运行前，请将程序目录“ele45”设置成MATLAB的运行目录 ●每一次实验之前都必须首先执行start命令 ●对于每一个函数，我们可以采用“help函数名”获得该函数的详细使用帮助， -VI-

―VI― 字体和印刷约定 本教材的一些习惯用法： l 斜体字用来表示它是 MATLAB 函数名,有时也表示强调,例如： 利用 MATLAB 函数 gaus_pdf 和 gaus_cdf 显示随机变量的概率密度函数和分布函数。 l “>>”符号是 MATLAB 的提示符,运行 MATLAB 后在你的终端上会出现此符号。有时 则由于 MATLAB 版本或设置的不同,在 MATLAB 的命令窗口中并没有此符号,但这 些都不会影响实验过程。 l 文本中的铅字（粗体字）表示它们是从 MATLAB 命令窗口得到的变量。你可以直接 调用其值进行计算。例如计算随机序列 abc 的均值和方差 >> mean_abc = mean(abc) ； var_abc = var(abc)； 其中 mean_abc 和 var_abc 分别代表 abc 的均值和方差。 l 出现在文本行中首字母大写的单词是你应键入的命令。例如： 如果 eye_diag 函数的第二个参数是负的,要显示下一个轨迹请敲击“Enter”键,这里的 “Enter”就是你必须键入的命令。 l 出现在黑线框中的问题是课后作业,这些问题必须以书面形式完成并在做下一次实 验之前交给指导教师。最后实验成绩评定时也要以此为参考。例如： 问题 1.2 如果分布率是基于 2000 次实验的结果,计算每面发生的次数。 l 为了实现在通信系统工具包（Communication System Toolbox）内部的通信,大量的 MATLAB 全局变量是必不可少的。MATLAB 的 start 函数会为每一个实验中所用全 局变量赋以必要的初值。进入 MATLAB 工作站进行实验的第一步,你必须首先执行下 面的命令： >> start 之后,你会得到一个友好的界面,它会给你提供一些其它信息。 请切记： l 安装 MATLAB 时,请安装”Signal Processing”库 l 运行前,请将程序目录“ele45”设置成 MATLAB 的运行目录 l 每一次实验之前都必须首先执行 start 命令 l 对于每一个函数,我们可以采用“help 函数名”获得该函数的详细使用帮助

实验三数字信号的基带传输 [实验目的： 在这个实验中我们将观察到二进制信息是如何进行编码的。我们将主要了解： ●目前用干数字桶信的基带码型 ●不同码型的功率谱密度 。信道失真的原因 ●通过眼图观察码间串扰和信道噪声的影响 [参考文献]： 1.沈振元等，“通信系统原理”，西安电子科技大学出版社，1993 2.曹志刚，钱亚生，“现代通信原理”，清华大学出版社，1992 3.王立宁等编，“MATLAB与通信仿真”，人民邮电出版社，2000 [预习作业： 1.给出二进制序列b1,0,1,0,11,用如下的码型绘出代表序列b的波形草图： a单极性不归零码 b双极性不归零码 c单极性归零码 d双极性归零码 e曼彻斯特码(manchester)(即成对的二进制码) 2.此处假定为单位幅度并且码元速率R=kbs。确定并绘出以上码型的功率谱密度函 数。令F>0为功率谱密度函数中第一个零点的位置。假设各个码型的传输带宽B=F, 那么请确定第1问中各种码型的带宽，并由此观察R的作用。 3.y)代表采用双极性不归零码编码的信道输出波形。为了显示眼图，将y(①)送入水平扫 描时间为3T,的示波器中，绘出相应眼图。 1,5r 0.5 -15

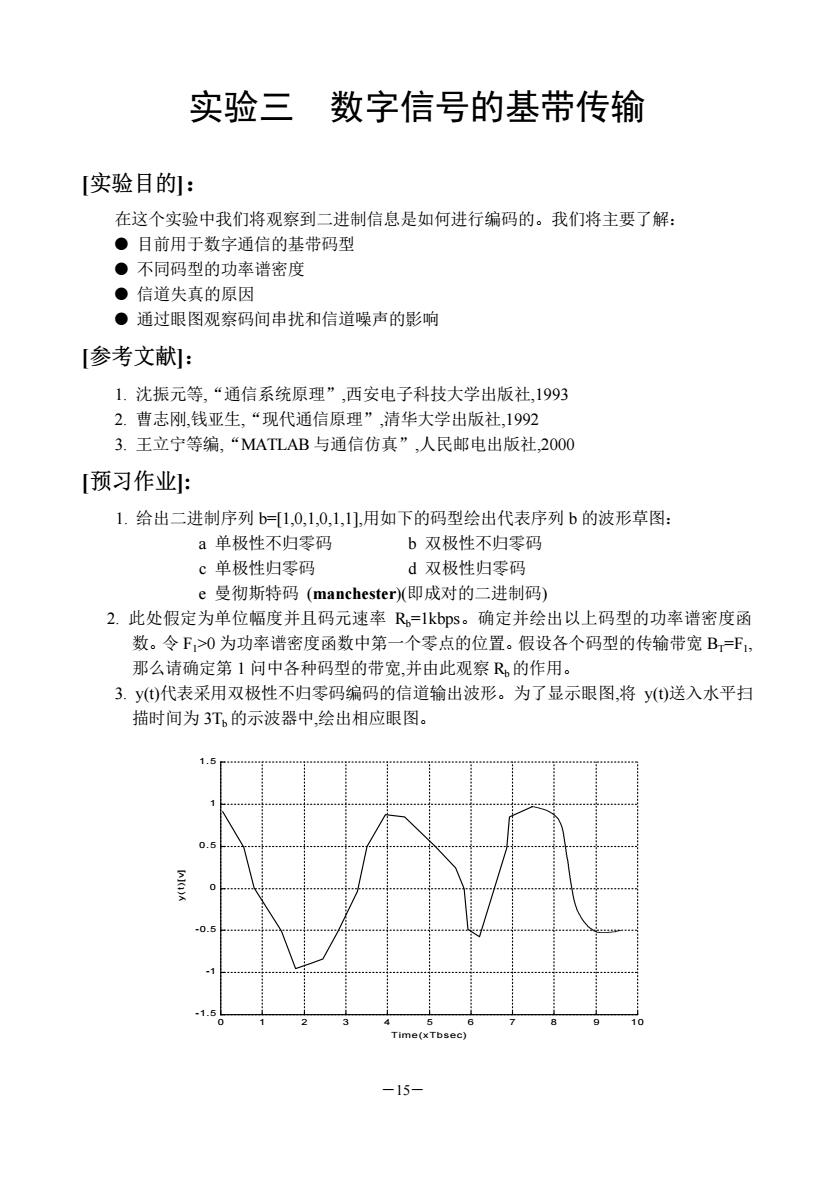
―15― 实验三 数字信号的基带传输 [实验目的]： 在这个实验中我们将观察到二进制信息是如何进行编码的。我们将主要了解： l 目前用于数字通信的基带码型 l 不同码型的功率谱密度 l 信道失真的原因 l 通过眼图观察码间串扰和信道噪声的影响 [参考文献]： 1. 沈振元等,“通信系统原理”,西安电子科技大学出版社,1993 2. 曹志刚,钱亚生,“现代通信原理”,清华大学出版社,1992 3. 王立宁等编,“MATLAB 与通信仿真”,人民邮电出版社,2000 [预习作业]: 1. 给出二进制序列 b=[1,0,1,0,1,1],用如下的码型绘出代表序列 b 的波形草图： a 单极性不归零码 b 双极性不归零码 c 单极性归零码 d 双极性归零码 e 曼彻斯特码 (manchester)(即成对的二进制码) 2. 此处假定为单位幅度并且码元速率 Rb=1kbps。确定并绘出以上码型的功率谱密度函 数。令 F1>0 为功率谱密度函数中第一个零点的位置。假设各个码型的传输带宽 BT=F1 , 那么请确定第 1 问中各种码型的带宽,并由此观察 Rb 的作用。 3. y(t)代表采用双极性不归零码编码的信道输出波形。为了显示眼图,将 y(t)送入水平扫 描时间为 3Tb 的示波器中,绘出相应眼图。 0 1 2 3 4 5 6 7 8 9 10 -1.5 -1 -0.5 0 0.5 1 1.5 Time(xTbsec) y(t)[v]

实验步骤： A.常用码型 A.1使用MATLAB函数wave gen来产生代表二进制序列的波形，函数wave gen的格式是： wave_gen((二进制码元，码型'，R) 此处R,是二进制码元速率，单位为比特/秒(bs)。产生如下的二进制序列： >b=[101011 使用R,=100Obps的单极性不归零码产生代表b的波形且显示波形x: >>x=wave_gen(b,'unipolar_nrz',1000). >waveplot(x) A.2用如下码型重复步骤A1(提示：可以键入“help wave_gen”来获取帮助) a双极性不归零码 b单极性归零码 c双极性归零码 d受仞斯特码(nanchester) 问题3.1由上述码型确定的哪些波形在任何情况下始终没有直流成份？为什么 直流成份的缺少对波形传输有特殊的意义？ A3码型的功率谱密度函数 产生一个1000个样值的二进制序列： >>b=binary(1000). 显示A.1使用的单极性不归零码的功率谱密度函数(PSD),并记录在表3.1中： psd(wave gen() 定义：Fpl:第一个谱峰 Fml:第一个频谱零点 Fp2:第二个谱峰. Fnl:第二个频谱零点 使用其它四种不同的码型，在表3.1中记录你观察到的数据： 表3.1 R=1000 Fpl Fnl Fp2 Fn2 B 单极性不归零码 双极性不归零码 单极性归零码 双极性归零码 曼彻斯特码 (Manchester) 注意：第一个频谱零点的位置决定传输带宽B A4为了显示PSD函数对二进制码率的依赖我们用曼彻斯特码和不同的R,来证实这点 >>psd(wave gen(b,'manchester',Rs)); 此处R取5kbps,10kbps,20kbps三个值，你也可用A.1中的其他码型来取代曼彻斯特码。 -16-

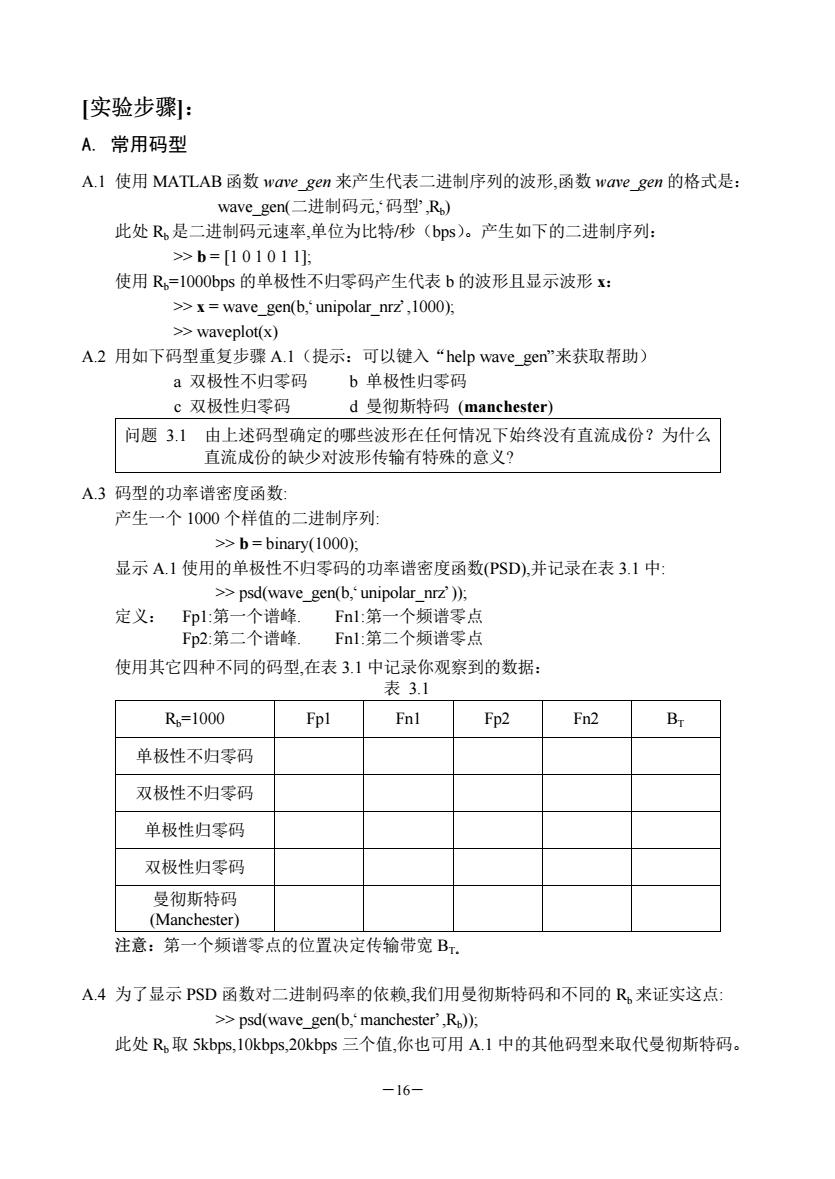
―16― [实验步骤]： A. 常用码型 A.1 使用 MATLAB 函数 wave_gen 来产生代表二进制序列的波形,函数 wave_gen 的格式是： wave_gen(二进制码元,‘码型’,Rb ) 此处 Rb 是二进制码元速率,单位为比特/秒（bps）。产生如下的二进制序列： >> b = [1 0 1 0 1 1]; 使用 Rb=1000bps 的单极性不归零码产生代表 b 的波形且显示波形 x： >> x = wave_gen(b,‘unipolar_nrz’,1000); >> waveplot(x) A.2 用如下码型重复步骤 A.1（提示：可以键入“help wave_gen”来获取帮助） a 双极性不归零码 b 单极性归零码 c 双极性归零码 d 曼彻斯特码 (manchester) 问题 3.1 由上述码型确定的哪些波形在任何情况下始终没有直流成份？为什么 直流成份的缺少对波形传输有特殊的意义? A.3 码型的功率谱密度函数: 产生一个 1000 个样值的二进制序列: >> b = binary(1000); 显示 A.1 使用的单极性不归零码的功率谱密度函数(PSD),并记录在表 3.1 中: >> psd(wave_gen(b,‘unipolar_nrz’)); 定义： Fp1:第一个谱峰. Fn1:第一个频谱零点 Fp2:第二个谱峰. Fn1:第二个频谱零点 使用其它四种不同的码型,在表 3.1 中记录你观察到的数据： 表 3.1 Rb=1000 Fp1 Fn1 Fp2 Fn2 BT 单极性不归零码 双极性不归零码 单极性归零码 双极性归零码 曼彻斯特码 (Manchester) 注意：第一个频谱零点的位置决定传输带宽 BT。 A.4 为了显示 PSD 函数对二进制码率的依赖,我们用曼彻斯特码和不同的 Rb 来证实这点: >> psd(wave_gen(b,‘manchester’,Rb )); 此处 Rb 取 5kbps,10kbps,20kbps 三个值,你也可用 A.1 中的其他码型来取代曼彻斯特码

同时观察谱峰和零点的位置及他们与R,的关系。 问题3.2对一个可用带宽为10KHz的基带通信信道而言，A.1中每一个码型的最 大码元速率为多少？ B.信道特性 在这一部分你将模拟一个通信信道的特点。代表信道响应的MATLAB函数是channel. 形式如下（提示：我们可以键入help channel来获取channel函数的帮助）： channel(输入，增益，噪声功率，带宽) 噪声 信道 输出 (增益)》 输入 图3.1信道模型 B.1创建一个有10个抽样值的二进制序列b且用双极性不归零信号格式产生代表b的波形 其中R=1kbps。 >b=binary(10). >>x=wave gen(b,'polar nrz',1000). 根据A部分的数据，确定x的传输带宽B: B.= Hz B.2考虑一个具有归一化增益和加性白高斯噪声(AWGN的基带数字传输信道（噪声功率为 102w信道带宽为4.9KHZ),在此信道上传输波形x并显示输入和输出波形： >y=channel(x1,0.01,4900)方 >>subplot(211),waveplot(x). >>subplot(212).waveplot(y): 根据显示的输出波形估计b: b- ],把你的估计和原序列b比较 B.3信道噪声对传输波形的影响。逐渐地增加信道噪声功率，并保持信道带宽不变，我们可 以观察信道输出的变化： >>subplot(212),waveplot(channel(x,1,sigma,4900)); gma取0.1,0.51,2,5等值。在噪声功率为多少时，我们传输的信号将淹没在噪声之中 B.4你也可以通过看信道输出的功率谱密度来观察增加信道噪声功率的影响： >>b=binary(1000); >>x=wave gen(b,polar nrz,1000) >>clf.subplot(121).psd(x).a=axis. >>subplot(122),psd(channel(x,1,0.01,4900)); >>axis(a)hold on -17

―17― 同时观察谱峰和零点的位置及他们与 Rb的关系。 问题 3.2 对一个可用带宽为 10KHz 的基带通信信道而言,A.1 中每一个码型的最 大码元速率为多少? B.信道特性 在这一部分你将模拟一个通信信道的特点。代表信道响应的 MATLAB 函数是 channel, 形式如下（提示：我们可以键入 help channel 来获取 channel 函数的帮助）: channel(输入,增益,噪声功率,带宽) B.1 创建一个有 10 个抽样值的二进制序列 b 且用双极性不归零信号格式产生代表 b 的波形, 其中 Rb=1kbps。 >> b = binary(10); >> x = wave_gen(b,’polar_nrz’,1000); 根据 A 部分的数据,确定 x 的传输带宽 BT： BT = Hz B.2 考虑一个具有归一化增益和加性白高斯噪声(AWGN)的基带数字传输信道(噪声功率为 10-2w,信道带宽为 4.9KHZ),在此信道上传输波形 x,并显示输入和输出波形: >> y = channel( x,1,0.01,4900 ); >> subplot(211),waveplot(x); >> subplot(212),waveplot(y); 根据显示的输出波形估计 b: b ^ =[ ],把你的估计和原序列 b 比较。 B.3 信道噪声对传输波形的影响。逐渐地增加信道噪声功率，并保持信道带宽不变,我们可 以观察信道输出的变化: >> subplot(212),waveplot( channel(x,1,sigma,4900)); sigma 取 0.1,0.5,1,2,5 等值。在噪声功率为多少时,我们传输的信号将淹没在噪声之中? B.4 你也可以通过看信道输出的功率谱密度来观察增加信道噪声功率的影响: >> b = binary(1000); >> x = wave_gen(b,‘polar_nrz’,1000); >> clf,subplot(121),psd(x),a = axis; >> subplot(122),psd(channel(x,1,0.01,4900)); >> axis(a),hold on 信道 （增益） 输入 输出 噪声 图 3.1 信道模型

>>psd(channel(x,1,1,4900)): >>psd(channel(x,1,5,4900)): 问题3.3由于信道噪声是加性噪声，且与输入信号无关，请问如何用信号功率谱 密度和噪声功率谱密度来表示信道输出的功率谱密度？ B.5信道带宽对传输波形的影响 在信道输出的时域显示中观察到的失真是由于有限的带宽和噪声的缘故。为了研究由 于信道带宽而造成的失真，我们设噪声的功率为0且重新产生信道输出波形： >>clf >>b=binary(10), >>x=wave _gen(b,'polar_nrz',1000); >>subplot(211),waveplot(x). >>subplot(212),waveplot(channel(x,1,0,4900)); B.6观察信道带宽对输出波形的影响 >>subplot(212),waveplot(channel(x.1.0.b.)): b.取值为3000,2000,1000,500。观察由于信道滤波特性而在输出波形上的时延并绘出输 入和输出波形 7 带宽 49 20H 0.5H me bo 图3.2 -18

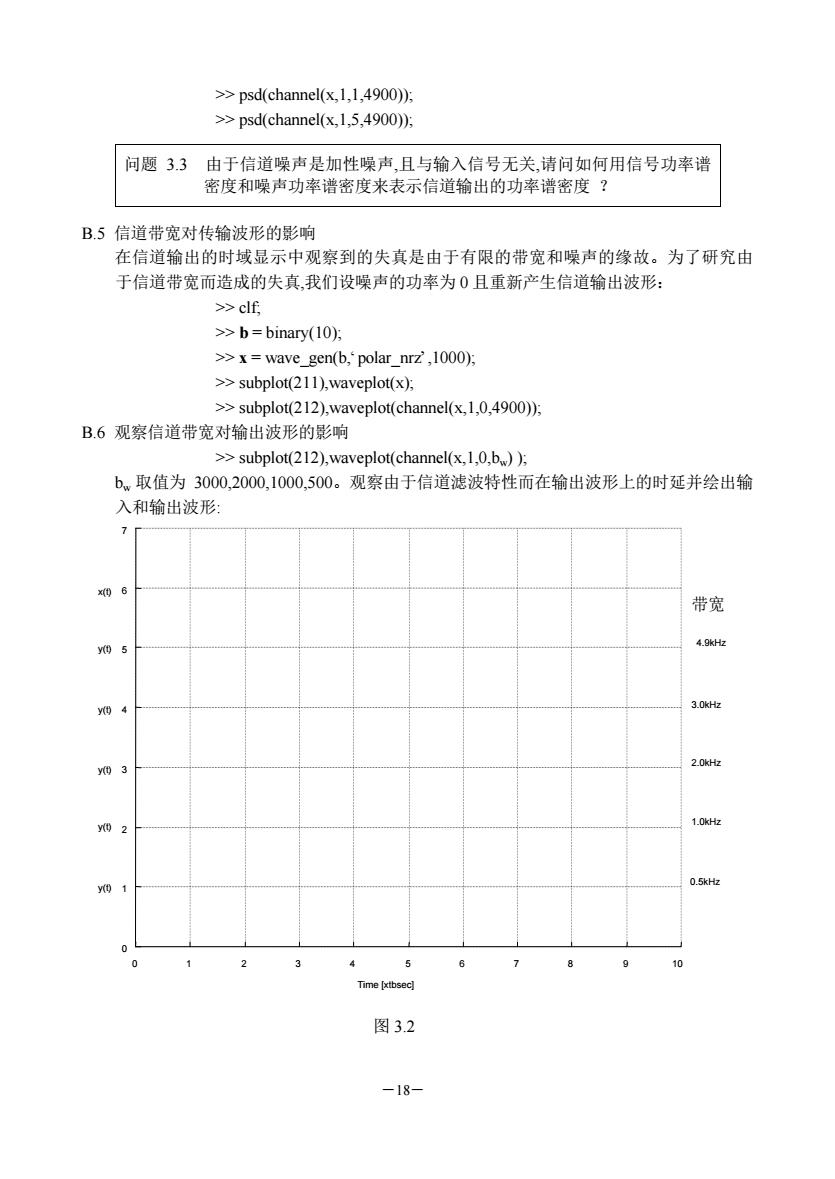
―18― >> psd(channel(x,1,1,4900)); >> psd(channel(x,1,5,4900)); 问题 3.3 由于信道噪声是加性噪声,且与输入信号无关,请问如何用信号功率谱 密度和噪声功率谱密度来表示信道输出的功率谱密度 ？ B.5 信道带宽对传输波形的影响 在信道输出的时域显示中观察到的失真是由于有限的带宽和噪声的缘故。为了研究由 于信道带宽而造成的失真,我们设噪声的功率为 0 且重新产生信道输出波形： >> clf; >> b = binary(10); >> x = wave_gen(b,‘polar_nrz’,1000); >> subplot(211),waveplot(x); >> subplot(212),waveplot(channel(x,1,0,4900)); B.6 观察信道带宽对输出波形的影响 >> subplot(212),waveplot(channel(x,1,0,bw) ); bw 取值为 3000,2000,1000,500。观察由于信道滤波特性而在输出波形上的时延并绘出输 入和输出波形: 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 Time [xtbsec] x(t) y(t) y(t) y(t) y(t) y(t) 带宽 4.9kHz 3.0kHz 2.0kHz 1.0kHz 0.5kHz 图 3.2

C.眼图 信道和噪声的影响可以通过眼图看出。眼图由数个扫描波形重叠而形成，每一扫描波形 由一个时钟信号控制，且扫描宽度比二进制码元持续时间T。=1/R稍长，在本试验中，眼 图是基于2T,宽的扫描而得到的。 C1眼图的产生 >>b=binary(20); >>x=wave_gen(b,'polar_nrZ,1000). >clf >subplot(221),waveplot(x). >>subplot(223),eye_diag(x); x的眼图代表了对于一个不失真信号你应该看到的东西。用下式观察如何产生眼图并且 观察一下x通过一个有限带宽的，无噪声的信道时信号失真的效果： >>y=channel(x,1,0.2000); >>subplot(222),waveplot(y); >>subplot(224).eye_diag(y,-1) 你必须敲击'Eter键10次，程序将自动绘制眼图，这将帮助你理解眼图是如何产生的。 C2度量一个眼图的关键参数如下 眼图 3 02 040.6 0.8 12 14 16 18 Time [sec] 图3.3眼图 A波形可被抽样的最大时间间隔B噪声容限 C时零点瞌变 D斜率：对定时误差的灵敏度 E最大信号畸变 F最佳抽样时刻 时钟信号既可由外部提供，也可从信道输出获得。它被用作示波器的外部控制输入

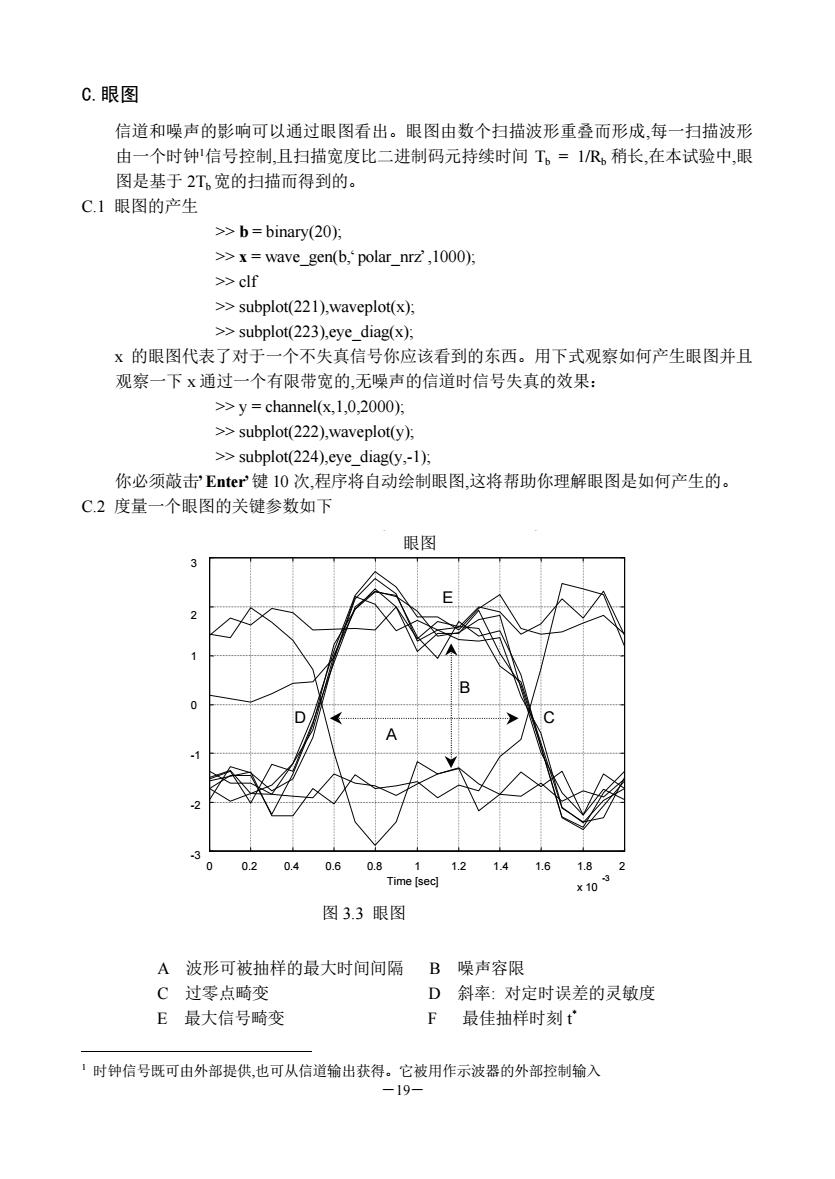
―19― C.眼图 信道和噪声的影响可以通过眼图看出。眼图由数个扫描波形重叠而形成,每一扫描波形 由一个时钟1信号控制,且扫描宽度比二进制码元持续时间 Tb = 1/Rb 稍长,在本试验中,眼 图是基于 2Tb 宽的扫描而得到的。 C.1 眼图的产生 >> b = binary(20); >> x = wave_gen(b,‘polar_nrz’,1000); >> clf >> subplot(221),waveplot(x); >> subplot(223),eye_diag(x); x 的眼图代表了对于一个不失真信号你应该看到的东西。用下式观察如何产生眼图并且 观察一下 x 通过一个有限带宽的,无噪声的信道时信号失真的效果： >> y = channel(x,1,0,2000); >> subplot(222),waveplot(y); >> subplot(224),eye_diag(y,-1); 你必须敲击’Enter’键 10 次,程序将自动绘制眼图,这将帮助你理解眼图是如何产生的。 C.2 度量一个眼图的关键参数如下 A 波形可被抽样的最大时间间隔 B 噪声容限 C 过零点畸变 D 斜率: 对定时误差的灵敏度 E 最大信号畸变 F 最佳抽样时刻 t * 1 时钟信号既可由外部提供,也可从信道输出获得。它被用作示波器的外部控制输入 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 x 10 -3 -3 -2 -1 0 1 2 3 Time [sec] 眼图 E B A D C 图 3.3 眼图

最佳抽样时刻是眼图中张开最大处的时间，如在图3.3中，为0.0008秒。如果二进 制码周期为T。那么为了进行信号检测我们将在t,t+T。+2工。等处对波形抽样，然后 利用这些判决值进行判决。请采用双极性不归零波形产生一个眼图，噪声功率siga和 信道带宽b.显示在表3.2中，对每一组sigma、b,记录t*、A、B的值（提示：将不同 的噪声功率sigma和信道带宽b代入函数y-channel(x.1,.sigma.b).中即可)。 表3.2 双极性不归零码 sigma be t B 3000 0.01 2000 1000 0.02 0.08 4000 0.10 C.3用曼彻斯特码型重做C.2步并记录结果。 表3.3 曼彻斯特码 sigma bw A 3000 0.01 2000 1000 0.02 0.08 4000 0.10 问题3.4在sigma=0.01和b.=1000的情况下，比较C.2和C.3眼图，你认为哪一个 码型有“较好的”眼图？并根据码型各自的优点来解释这种现象！ C.4按照步骤C.2分别用双极性归零码，单极性归零码和单极性不归零码来产生眼图，并观察 码型是如何确定眼图的形状和对称性的。 -20

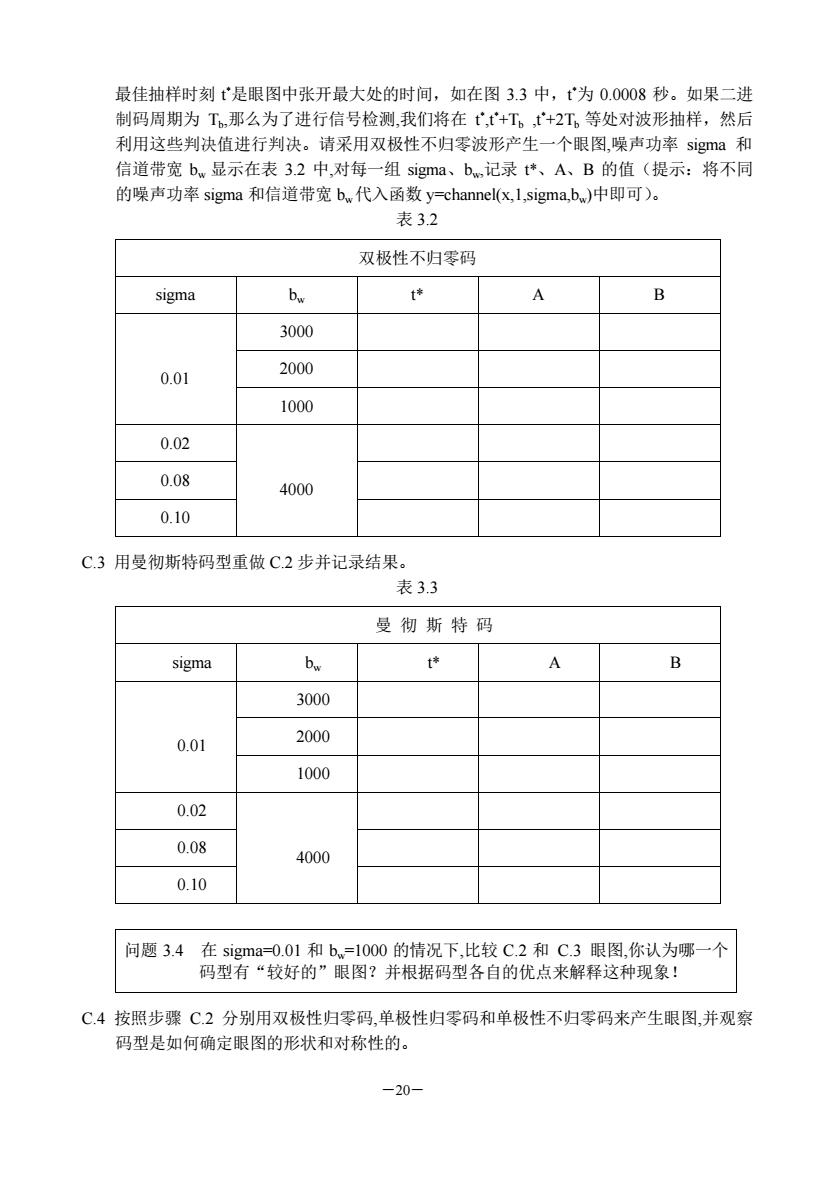
―20― 最佳抽样时刻 t *是眼图中张开最大处的时间，如在图 3.3 中，t *为 0.0008 秒。如果二进 制码周期为 Tb ,那么为了进行信号检测,我们将在 t * ,t*+Tb ,t*+2Tb 等处对波形抽样，然后 利用这些判决值进行判决。请采用双极性不归零波形产生一个眼图,噪声功率 sigma 和 信道带宽 bw 显示在表 3.2 中,对每一组 sigma、bw,记录 t*、A、B 的值（提示：将不同 的噪声功率 sigma 和信道带宽 bw代入函数 y=channel(x,1,sigma,bw)中即可）。 表 3.2 双极性不归零码 sigma bw t* A B 3000 2000 0.01 1000 0.02 0.08 0.10 4000 C.3 用曼彻斯特码型重做 C.2 步并记录结果。 表 3.3 曼 彻 斯 特 码 sigma bw t* A B 3000 2000 0.01 1000 0.02 0.08 0.10 4000 问题 3.4 在 sigma=0.01 和 bw=1000 的情况下,比较 C.2 和 C.3 眼图,你认为哪一个 码型有“较好的”眼图？并根据码型各自的优点来解释这种现象！ C.4 按照步骤 C.2 分别用双极性归零码,单极性归零码和单极性不归零码来产生眼图,并观察 码型是如何确定眼图的形状和对称性的

实验四【 匹配滤波器信号检测 [实验目的]： 在这个实验中，你将学习到以下内容 ●观察匹配滤波器的特性。 ●通过测量误码率来研究基于不同滤波器的接收机的性能。 ●用眼图来设置检测过程中的参数。 [参考文献]： 1.沈振元等，“通信系统原理”，西安电子科技大学出版社，1993 2.曹志刚.钱亚生.“现代通信原理”清华大学出版社.1992 3.王立宁等编，“MATLAB与通信仿真”，人民邮电出版社，2000 [预习作业] 1.讨论用来检测方波r0=ec一工。凸)的匹配滤波器T,=1ms: 如果(0是输 确定匹配 滤波器的输 c.对一个码元周期为10ms的三角波重复a,b。 2.设))叶O,代表信道输出的波形。0是单位幅度的双极性不归零波形，且码率 R,为1kbps。n()是一个功率谱密度为： S(f)=N。/2=0.5×104W1H 的白噪声过程。如果通讨一匹配滤波器： a确定E,(即一比特期间X)的平均能量)。 b.确定在匹配滤波器输出端信号幅度的峰值和噪声的均方值。 c确定误比特率户=Q(,不，)《Q)-方，函最咏可以用 MATLAB计算。) -21

―21― 实验四 匹配滤波器信号检测 [实验目的]: 在这个实验中,你将学习到以下内容: l 观察匹配滤波器的特性。 l 通过测量误码率来研究基于不同滤波器的接收机的性能。 l 用眼图来设置检测过程中的参数。 [参考文献]: 1. 沈振元等,“通信系统原理”,西安电子科技大学出版社,1993 2. 曹志刚,钱亚生,“现代通信原理”,清华大学出版社,1992 3. 王立宁等编,“MATLAB 与通信仿真”,人民邮电出版社,2000 [预习作业] 1. 讨论用来检测方波 ) / 2 ( ) ( b b T t T r t rect - = 的匹配滤波器(Tb=1ms)： a. 确定匹配滤波器的脉冲响应波形。 b. 如果 r(t)是输入,确定匹配滤波器的输出。 c. 对一个码元周期为 10ms 的三角波重复 a,b。 2. 设 Y(t)=X(t)+n(t),代表信道输出的波形。X(t)是单位幅度的双极性不归零波形,且码率 Rb 为 1 kbps。n(t)是一个功率谱密度为： S f N W Hz n ( ) / 2 0.5 10 / 4 0 - = = ´ 的白噪声过程。如果 Y(t)通过一匹配滤波器： a. 确定 Eb (即一比特期间 X(t)的平均能量)。 b. 确定在匹配滤波器输出端信号幅度的峰值和噪声的均方值。 c. 确定误比特率: ) 2 ( N 0 E P Q b e = ，（ ) 2 ( 2 1 ( ) x Q x = erfc ，函数 erfc 可以用 MATLAB 计算。）