《通信原理》第九章.差错控制编码习题 第九章差错控制编码 习题(30道) [100000000001100] 010000000000110 001000000000011 「xg(x) 000100000000010 x'g(x) 000010000001010 1.已知(15,1)汉明码的生成矩阵: 000001000000101 试求其生成多项式 000000100001110 g(x) 000000010000111 000000001001111 000000000101011 000000000011001 和监督矩阵。 100010101111000 解:监督阵H 110001111000100 011110111100010 001001011110001 生成多项式为gx=x4+x3+1 100010101111000 10001111000100 2.已知(15,11)汉明码的监督阵H= 试求其生成矩阵和生成多项式。 011110111100010 001001011110001 T100000000001100 010000000000110 001000000000011 「xg(x) 000100000000010 x’g(x) 000010000001010 解: 生成矩阵G 000001000000101 000000100001110 g(x) 000000010000111 000000001001111 000000000101011 000000000011001 生成多项式为g(x)=x4+x3+1
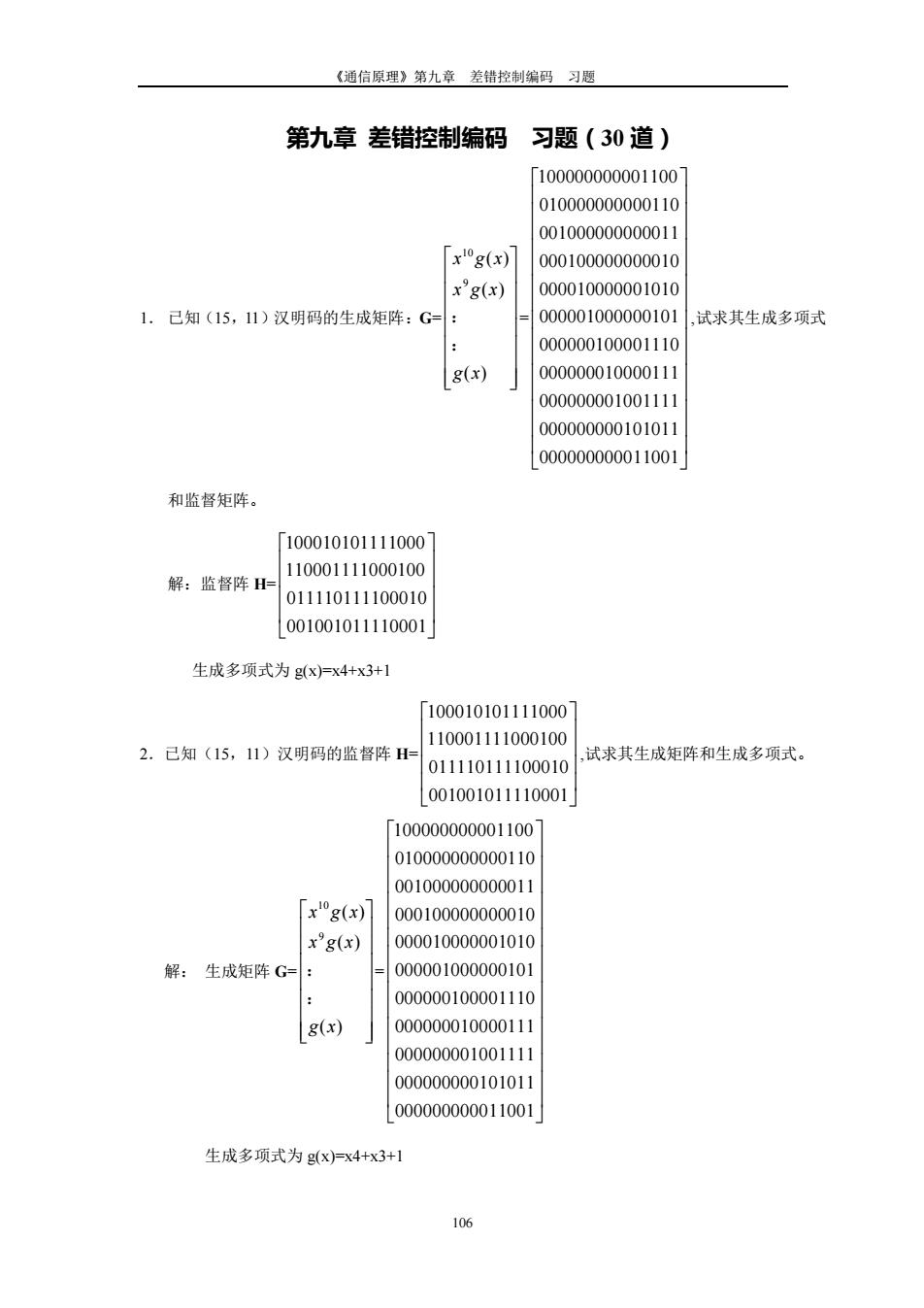
《通信原理》第九章 差错控制编码 习题 106 第九章 差错控制编码 习题(30 道) 1. 已知(15,11)汉明码的生成矩阵:G= ( ) ( ) ( ) 9 10 g x x g x x g x : : = 000000000011001 000000000101011 000000001001111 000000010000111 000000100001110 000001000000101 000010000001010 000100000000010 001000000000011 010000000000110 100000000001100 ,试求其生成多项式 和监督矩阵。 解:监督阵 H= 001001011110001 011110111100010 110001111000100 100010101111000 生成多项式为 g(x)=x4+x3+1 2.已知(15,11)汉明码的监督阵 H= 001001011110001 011110111100010 110001111000100 100010101111000 ,试求其生成矩阵和生成多项式。 解: 生成矩阵 G= ( ) ( ) ( ) 9 10 g x x g x x g x : : = 000000000011001 000000000101011 000000001001111 000000010000111 000000100001110 000001000000101 000010000001010 000100000000010 001000000000011 010000000000110 100000000001100 生成多项式为 g(x)=x4+x3+1

《通信原理》第九章差错控制编码习题 x14+x12+x9+x8+x6+x5+x4 x13+xl1+x8+x7+x5+x4+x3 3.生成矩阵:G(x) x12+x10+x7+x6+x4+x3+x2 写出消息码的m(x)x4+x+1 x11+x9+x6+x5+x3+x2+x x10+x8+x5+x4+x2+x+1 的码多项式和生成多项式。 解:生成多项式:x10+x8+x5+x4+x2+x+1 因为m(x=x4+x+1 x10.m(x)=x14+x11+x10 xlOm(x)/g(x)=r(x)=x8+x7+x6+x 所以,Tx)=x14+x11+x10+x8+x7+x6+x 4.(15,5)循环码的消息码的m(xFx4+x+1的码多项式为T(x)=x14+x11+x10+x8+x7+x6+x 求出该码的生成矩阵和生成多项式。 xl4+x12+x9+x8+x6+x5+x4 xl3+x11+x8+x7+x5+x4+x3 解:G(x=x12+x10+x7+x6+x4+x3+x2 x11+x9+x6+x5+x3+x2+x Lxl0+x8+x5+x4+x2+x+1 生成多项式:x10+x8+x5+x4+x2+x+1 5.已知某线性码所有许用码组为:0000000001010101001100110011 1000111101001011000011110100 0001011001111001011010111000 1001100101101011010101111111,列出监督矩阵。 [1110100 解:监督矩阵为H=1101010 1011001 6.己知某线性码所有许用码组为:0000000001010101001100110011 107
《通信原理》第九章 差错控制编码 习题 107 3. 生成矩阵:G(x)= + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + 10 8 5 4 2 1 11 9 6 5 3 2 12 10 7 6 4 3 2 13 11 8 7 5 4 3 14 12 9 8 6 5 4 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ,写出消息码的 m(x)=x4+x+1 的码多项式和生成多项式。 解:生成多项式:x10+x8+x5+x4+x2+x+1 因为 m(x)=x4+x+1 x10.m(x)=x14+x11+x10 x10m(x)/g(x)=r(x)=x8+x7+x6+x 所以,T(x)=x14+x11+x10+x8+x7+x6+x 4.(15,5)循环码的消息码的 m(x)=x4+x+1 的码多项式为 T(x)=x14+x11+x10+x8+x7+x6+x 求出该码的生成矩阵和生成多项式。 解:G(x)= + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + 10 8 5 4 2 1 11 9 6 5 3 2 12 10 7 6 4 3 2 13 11 8 7 5 4 3 14 12 9 8 6 5 4 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x , 生成多项式:x10+x8+x5+x4+x2+x+1 5.已知某线性码所有许用码组为:0000000 0010101 0100110 0110011 1000111 1010010 1100001 1110100 0001011 0011110 0101101 0111000 1001100 1011010 1101010 1111111,列出监督矩阵。 解:监督矩阵为 H= 1011001 1101010 1110100 6.已知某线性码所有许用码组为:0000000 0010101 0100110 0110011

《通信原理》第九章差错控制编码习题 1000111101001011000011110100 0001011001111001011010111000 100110010110101101010111111L,列出生成矩阵 解:H=P G=Io] 10001111 所以生成矩阵为G= 0100110 0010101 0001011 7.己知(7,3)码的所以许用码组为: 0000000001110101001110111010 1001110101001111010011110100 求监督矩阵和生成矩阵。 T1001110 解:生成矩阵为G=0100111 0011101 「1011000 监督矩阵为= 1110100 1100010 0110001 1011000 1110100 8.己知(7,3)码的监督矩阵为H 1100010 列出所有许用码组,并求生成矩阵, 0110001 解:所以许用码组为: 0000000001110101001110111010 1001110101001111010011110100 g
《通信原理》第九章 差错控制编码 习题 108 1000111 1010010 1100001 1110100 0001011 0011110 0101101 0111000 1001100 1011010 1101010 1111111,列出生成矩阵 解:H=[PIr] G=[IkQ] 所以生成矩阵为 G= 0001011 0010101 0100110 1000111 7.已知(7,3)码的所以许用码组为: 0000000 0011101 0100111 0111010 1001110 1010011 1101001 1110100 求监督矩阵和生成矩阵。 解:生成矩阵为 G= 0011101 0100111 1001110 监督矩阵为 H= 0110001 1100010 1110100 1011000 8.已知(7,3)码的监督矩阵为 H= 0110001 1100010 1110100 1011000 列出所有许用码组,并求生成矩阵。 解: 所以许用码组为: 0000000 0011101 0100111 0111010 1001110 1010011 1101001 1110100

《通信原理》第九章差错控制编码习题 「1001110 生成矩阵为G=0100111 0011101 1000101 0100111 9.己知(7,4)循环码的生成矩阵G= 0010110 0001011 试写出该循环码的生成多项式x)和全部码组。 解:全部码组为 00000001000101 00010111001110 00101101010011 00111011011000 01001111100010 01011001101001 01100011110100 01110101111111 生成多项式gx)=x3+x+ 10.己知(7,4)循环码的生成多项式(x)=x3+x+1 试写出该循环码全部码组并求生成矩阵G(x,将Gx)化成典型阵。 解: 00000001000101 00010111001110 00101101010011 00111011011000 109
《通信原理》第九章 差错控制编码 习题 109 生成矩阵为 G= 0011101 0100111 1001110 9.已知(7,4)循环码的生成矩阵 G= 0001011 0010110 0100111 1000101 试写出该循环码的生成多项式 g(x)和全部码组。 解:全部码组为 0000000 1000101 0001011 1001110 0010110 1010011 0011101 1011000 0100111 1100010 0101100 1101001 0110001 1110100 0111010 1111111 生成多项式 g(x)=x3+x+1 10.已知(7,4)循环码的生成多项式 g(x)=x3+x+1 试写出该循环码全部码组并求生成矩阵 G(x),将 G(x)化成典型阵。 解: 0000000 1000101 0001011 1001110 0010110 1010011 0011101 1011000

《通信原理》第九章.差错控制编码习题 01001111100010 01011001101001 01100011110100 01110101111 x'g(x)][1011000 生成矩阵G(x)= x'g(x) _0101100 xg(x) 0010110 g(x) 0001011 对其进行初等变幻,可化成典型阵: [1000101 G= 0100111 0010110 0001011 11.已知某线性码所有许用码组为:000000000010110010101001110 0100110010110101100110111000 1000111100110010100101011001 110000111010101110100111111 求监督矩阵和生成矩阵 1110100 解:监督矩阵为H1101010 1011001 「1000111 0100110 生成矩阵为G 0010101 0001011 %
《通信原理》第九章 差错控制编码 习题 110 0100111 1100010 0101100 1101001 0110001 1110100 0111010 1111111 生成矩阵 G(x) = ( ) ( ) ( ) ( ) 2 3 g x xg x x g x x g x = 0001011 0010110 0101100 1011000 对其进行初等变幻,可化成典型阵: G= 0001011 0010110 0100111 1000101 11.已知某线性码所有许用码组为:0000000 0001011 0010101 0011110 0100110 0101101 0110011 0111000 1000111 1001100 1010010 1011001 1100001 1101010 1110100 1111111 求监督矩阵和生成矩阵 解:监督矩阵为 H= 1011001 1101010 1110100 , 生成矩阵为 G= 0001011 0010101 0100110 1000111

《通信原理》第九章差错控制编码习题 1000111 12.已知某线性码生成矩阵为G= 0100110 求所有许用码组和监督钜陈」 0010101 0001011 解:所有许用码组为:0000000000101100101010011110 0100110010110101100110111000 1000111100110010100101011001 1100001110101011101001111111 「1110100 监督矩阵为H=1101010 1011001 13.己知(7,4)码的所有许用码组为:000000000011000100110011101 0100101010101101101100111000 1000111100100110101001011010 110001011011001110001111111 ,写出生成矩阵,并求监督矩阵。 T1000111 解:生成矩阵为G=0100101 0001110 G=[IkQ] 「1101100 H=PIrF1011010 1110001 1101100 14.已知(7,4)码的监督矩阵为H=Pr]=1011010,写出所有许用码组,并求生成矩 1110001 年。 解:所有许用码组为:0000000000111000100110011101 11
《通信原理》第九章 差错控制编码 习题 111 12.已知某线性码生成矩阵为 G= 0001011 0010101 0100110 1000111 求所有许用码组和监督矩阵。 解:所有许用码组为:0000000 0001011 0010101 0011110 0100110 0101101 0110011 0111000 1000111 1001100 1010010 1011001 1100001 1101010 1110100 1111111 监督矩阵为 H= 1011001 1101010 1110100 13.已知(7,4)码的所有许用码组为:0000000 0001110 0010011 0011101 0100101 0101011 0110110 0111000 1000111 1001001 1010100 1011010 1100010 1101100 1110001 1111111 ,写出生成矩阵,并求监督矩阵。 解:生成矩阵为 G= 0001110 0100101 1000111 G=[IkQ] H=[PIr]= 1110001 1011010 1101100 14.已知(7,4)码的监督矩阵为 H=[PIr]= 1110001 1011010 1101100 ,写出所有许用码组,并求生成矩 阵。 解:所有许用码组为:0000000 0001110 0010011 0011101

《通信原理》第九章.差错控制编码习题 0100101010101101101100111000 1000111100100110101001011010 11000101101100111000111111 1000111 生成矩阵为G=0100101 0001110 15. 一个(15,7)的循环码的生成多项式位gx)x8+x7+x6+x4+1,求生成矩阵 111010001000000 [xg(x) 011101000100000 x'g(x) 001110100010000 解:G 000111010001000 000011101000100 g(x) 000001110100010 000000111010001 [111010001000000 「xg(x) 011101000100000 x'g(x) 001110100010000 16一个(15,7)的循环码的生成矩阵G=: 000111010001000,求信总多项式 000011101000100 8() 000001110100010 000000111010001 m(x)=x6+x3+x+1的码多项式c(x) 解:x8mxFx8(x6+x3+x+1) =x14+x11+x9+x8 (xl4+xll+x9+x8)/g(x)=x6+x5+x2+x+l+(x6+x4+x2+x+l)/g(x gx)=x8+x7+x6+x4+1 所以,r(x)=x6+x4+x2+x+1 么
《通信原理》第九章 差错控制编码 习题 112 0100101 0101011 0110110 0111000 1000111 1001001 1010100 1011010 1100010 1101100 1110001 1111111 生成矩阵为 G= 0001110 0100101 1000111 15. 一个(15,7)的循环码的生成多项式位 g(x)=x8+x7+x6+x4+1,求生成矩阵。 解:G= ( ) ( ) ( ) 5 6 g x x g x x g x : : = 000000111010001 000001110100010 000011101000100 000111010001000 001110100010000 011101000100000 111010001000000 16 一个(15,7)的循环码的生成矩阵 G= ( ) ( ) ( ) 5 6 g x x g x x g x : : = 000000111010001 000001110100010 000011101000100 000111010001000 001110100010000 011101000100000 111010001000000 ,求信息多项式 m(x)=x6+x3+x+1 的码多项式 c(x) 解:x8m(x)=x8(x6+x3+x+1) =x14+x11+x9+x8 (x14+x11+x9+x8)/g(x)=x6+x5+x2+x+1+( x6+x4+x2+x+1)/g(x) g(x)=x8+x7+x6+x4+1 所以,r(x)=x6+x4+x2+x+1

《通信原理》第九章差错控制编码习题 所以,码多项式为:x14+x11+x9+x8+x6+x4+x2+x+1 17己知两码组为(0011),(1100)。如用于检错,能检出几位错码?如用于纠错,能纠正几 位错码?如同时用于检错与纠错,问纠错,检错的性能如何? 解:最小码距d0=4 用于检错,do≥e+1,得e=3,所以能检三位错: 用于纠错,do≥2t+Lt=1,所以能位错 用于纠检错,d0≥e+t+1,得e=2,=1,所以能同时检2位错并纠正1位错码。 18己知两码组为(0001),(1110)。如用于检错,能检出几位错码?如用于纠错,能纠正几 位错码?如同时用于检错与纠错,间纠错,检错的性能如何? 解:最小码距do=4 用于检错,do≥e+1,得e=3,所以能检三位错: 用于纠错,do≥2t+1,得=1,所以能纠位错: 用于纠检错,do≥e+t+1,得e=2,仁1,所以能同时检2位错并纠正1位错码。 19(15,7)循环码由gx)=x5+x3+x+1生成,求hMx) 解:hx=(x5+1)Vgx) 所以h(x)x10+x8+x5+x4+x2+x+1 20(15,7)循环码由gx=x10+x8+x5+x4+x2+x+1生成,求hMx) 解:h(x=x5+1)Vg(x) 113
《通信原理》第九章 差错控制编码 习题 113 所以,码多项式为:x14+x11+x9+x8+x6+x4+x2+x+1 17 已知两码组为(0011),(1100)。如用于检错,能检出几位错码?如用于纠错,能纠正几 位错码?如同时用于检错与纠错,问纠错,检错的性能如何? 解: 最小码距 do=4 用于检错,do e +1,得e = 3,所以能检三位错; 用于纠错,do 2t +1,得t =1,所以能纠1位错; 用于纠检错,do e+t+1,得 e=2,t=1,所以能同时检 2 位错并纠正 1 位错码。 18 已知两码组为(0001),(1110)。如用于检错,能检出几位错码?如用于纠错,能纠正几 位错码?如同时用于检错与纠错,问纠错,检错的性能如何? 解:最小码距 do=4 用于检错,do e +1,得e = 3,所以能检三位错; 用于纠错,do 2t +1,得t =1,所以能纠1位错; 用于纠检错,do e+t+1,得 e=2,t=1,所以能同时检 2 位错并纠正 1 位错码。 19(15,7)循环码由 g(x)=x5+x3+x+1 生成,求 h(x). 解:h(x)=(x 15 +1)/g(x) 所以 h(x)=x10+x8+x5+x4+x2+x+1 20(15,7)循环码由 g(x)= x10+x8+x5+x4+x2+x+1 生成,求 h(x) 解:h(x)=(x 15 +1)/g(x)

《通信原理》第九章差错控制编码习题 所以hx=x5+x3+x+1 21.已知两码组为(0000),(1111)。如用于检错,能检出几位错码?如用于纠错,能纠正几位 错码?如同时用于检错与纠错,问纠错,检错的性能如何? 解:最小码距do=4 用于检错,do≥e+L,得e=3,所以能检三位错: 用于纠错,do≥21+1,得t=1,所以能纠位错: 用于纠检错,d0≥c+t+1,得c=2,=1,所以能同时检2位错并纠正1位错码 22.己知(15,11)汉明码的生成多项式g(x)-x4+x3+1,试求其生成矩阵和监督矩阵。 100000000001100 010000000000110 00100000000001 「xg(x) 000100000000010 x’g(x) 000010000001010 解:G =000001000000101 000000100001110 8(x) 000000010000111 000000001001111 000000000101011 000000000011001 100010101111000 110001111000100 故监督阵 011110111100010 001001011110001 23.证明x10+x8+x5+x4+x2+x+1为(15,5)循环码的生成多项式。求出该码的生成矩阵,并写 出消息码的mx)=x4+x+1的码多项式。 解:因为x15+1=(x+1)x4+x3+1)(x10+x8+x5+x4+x2+x+1) 114
《通信原理》第九章 差错控制编码 习题 114 所以 h(x)= x5+x3+x+1 21. 已知两码组为(0000),(1111)。如用于检错,能检出几位错码?如用于纠错,能纠正几位 错码?如同时用于检错与纠错,问纠错,检错的性能如何? 解:最小码距 do=4 用于检错,do e +1,得e = 3,所以能检三位错; 用于纠错,do 2t +1,得t =1,所以能纠1位错; 用于纠检错,do e+t+1,得 e=2,t=1,所以能同时检 2 位错并纠正 1 位错码。 22. 已知(15,11)汉明码的生成多项式 g(x)=x4+x3+1,试求其生成矩阵和监督矩阵。 解:G= ( ) ( ) ( ) 9 10 g x x g x x g x : : = 000000000011001 000000000101011 000000001001111 000000010000111 000000100001110 000001000000101 000010000001010 000100000000010 001000000000011 010000000000110 100000000001100 故监督阵 H= 001001011110001 011110111100010 110001111000100 100010101111000 23. 证明 x10+x8+x5+x4+x2+x+1 为(15,5)循环码的生成多项式。求出该码的生成矩阵,并写 出消息码的 m(x)=x4+x+1 的码多项式。 解:因为 x15+1=(x+1)(x4+x3+1)(x10+x8+x5+x4+x2+x+1)

《通信原理》第九章差错控制编码习题 所以g(x)=x10+x8+x5+x4+x2+x+1 「x14+x12+x9+x8+x6+x5+x4 x13+x11+x8+x7+x5+x4+x3 该码生成矩阵:G(x上xl2+x10+x7+x6+x4+x3+x2 x11+x9+x6+x5+x3+x2+x xl0+x8+x5+x4+x2+x+1 又因为mxx4+x+1 xl0.m(x)=x14+xll+xl0 xlOm(x)/g(x)=r(x)-x8+x7+x6+x 所以,Tx)=x14+x11+x10+x8+x7+x6+x 1110100 24. 已知某线性码监督矩阵为:H=1101010,列出所有许用码组。 1011001 解:H=P] [10001117 0100110 G=[kO]= 0010101 0001011 从而,许用码组[a6a5a4a3a2ala0a6a5a4a3]·G 所以许用码组为: 0000000001010101001100110011 1000111101001011000011110100 0001011001111001011010111000 10011001011010110101011111 115
《通信原理》第九章 差错控制编码 习题 115 所以 g(x)= x10+x8+x5+x4+x2+x+1 该码生成矩阵:G(x)= + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + 10 8 5 4 2 1 11 9 6 5 3 2 12 10 7 6 4 3 2 13 11 8 7 5 4 3 14 12 9 8 6 5 4 x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 又因为 m(x)=x4+x+1 x10.m(x)=x14+x11+x10 x10m(x)/g(x)=r(x)=x8+x7+x6+x 所以,T(x)=x14+x11+x10+x8+x7+x6+x 24. 已知某线性码监督矩阵为:H= 1011001 1101010 1110100 ,列出所有许用码组。 解:H=[PIr] G=[IkQ]= 0001011 0010101 0100110 1000111 从而,许用码组[a6a5a4a3a2a1a0]=[a6a5a4a3] • G 所以许用码组为: 0000000 0010101 0100110 0110011 1000111 1010010 1100001 1110100 0001011 0011110 0101101 0111000 1001100 1011010 1101010 1111111