《通信原理》第三章信道习趣 第三章信道习题(7道) 3-2设某恒参信道的频谱特性为 H ()=[1+cosTole 其中,七为常数。试确定信号s()通过该信道后的输出信号表示式,并讨论之。 解:设输出信号为s(t) s(t)e5(a):s(t)=5(a) S.()=S()H()=S(@)[l+coswTJe4 =S(o)[1+1/2·eo+1/2·em]ei =()eiu+1/2.()ei+1/2.s()e s(t)=s(t-ta+1/2·s(t+T-t+1/2·s(t-T-ta 讨论:该恒参信道的幅频特性和相频特性分别如下图所示: ↑1H(ojl=1+cosoTo ,φ(o)-ot 0T63/T。 该恒参信道对信号产生选择性衰落失真。 3-4今有两个恒参信道,其等效模型分别如图P3-2()、(b)所示,试求这两个信道的群迟延特 性,并画出它们的群迟延曲线,同时说明信号通过它们时有无群迟延失真? 。口R (a) 图P3-2 (b) 第18项
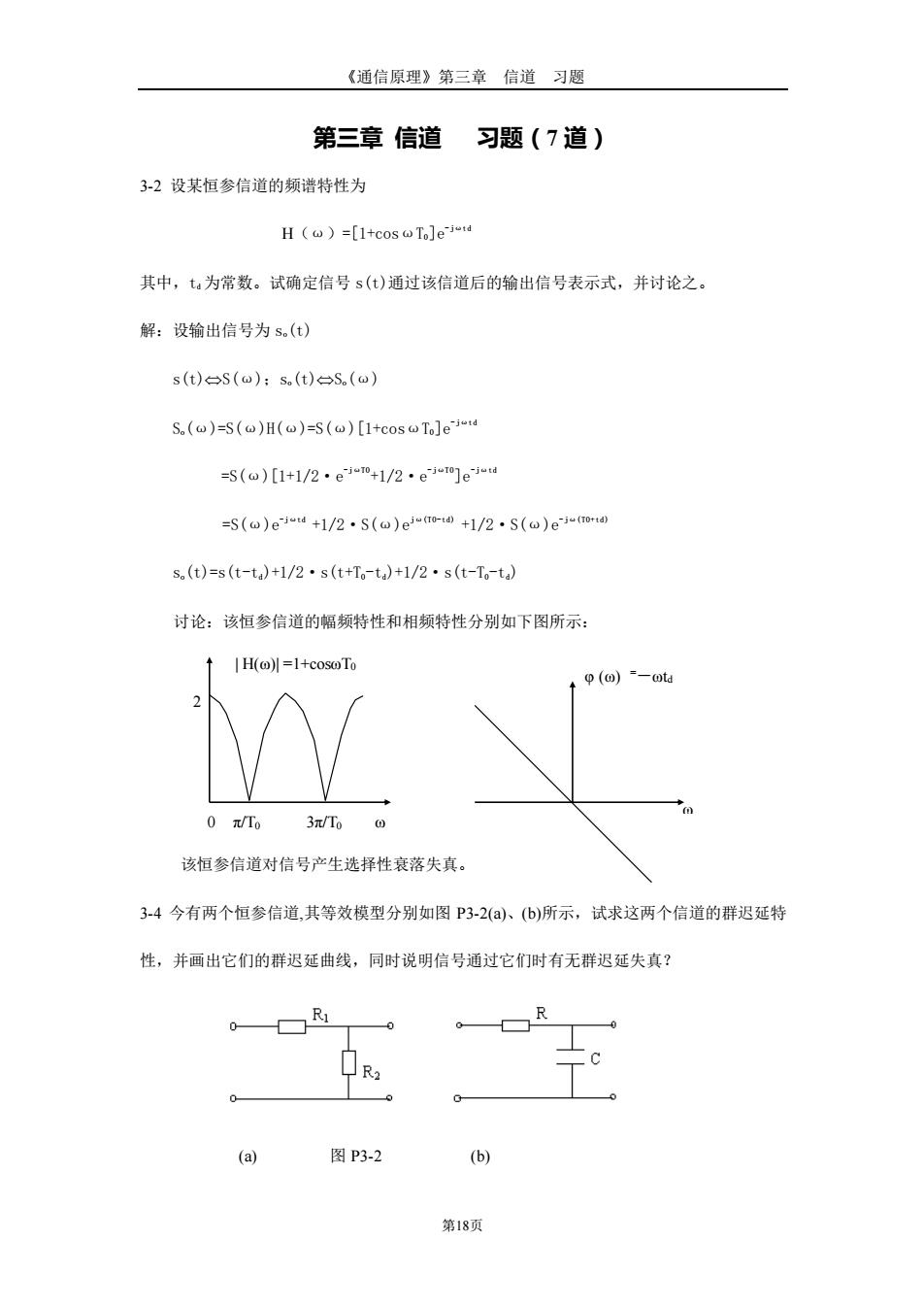
《通信原理》第三章 信道 习题 第18页 第三章 信道 习题(7 道) 3-2 设某恒参信道的频谱特性为 H(ω)=[1+cosωT0]e-jωtd 其中,td 为常数。试确定信号 s(t)通过该信道后的输出信号表示式,并讨论之。 解:设输出信号为 so(t) s(t)S(ω);so(t)So(ω) So(ω)=S(ω)H(ω)=S(ω)[1+cosωT0]e-jωtd =S(ω)[1+1/2·e -jωT0+1/2·e -jωT0]e-jωtd =S(ω)e-jωtd +1/2·S(ω)ejω(T0-td) +1/2·S(ω)e-jω(T0+td) so(t)=s(t-td)+1/2·s(t+T0-td)+1/2·s(t-T0-td) 讨论:该恒参信道的幅频特性和相频特性分别如下图所示: 该恒参信道对信号产生选择性衰落失真。 3-4 今有两个恒参信道,其等效模型分别如图 P3-2(a)、(b)所示,试求这两个信道的群迟延特 性,并画出它们的群迟延曲线,同时说明信号通过它们时有无群迟延失真? (a) 图 P3-2 (b) H(ω) =1+cosωT0 φ (ω) =-ωtd ω 0 π/T0 3π/T0 ω 2

《通信原理》第三章信道习题 解:对(a)H(o)=RR1+R2) lH()l=R:/(Ri+Rz) 中(o)=0 do上.dΦ(o)Wdo=0 “信号通过该信道时无群迟延失真。 对b)H(o上1/1中joRC) 1H(o)1=/1+oRC φ(u-arctg(oRC) ta()=-d()/do=RC/(l+2R2C) “信号通过该信道时有群迟延失真 38假设某随参信道的两径时延差为1ms,试求该信道在哪些频率上传输衰耗最大?所传输 的信号选用哪些频率传输最有利? 解:1=lms 当n/t=nkHz时(n为整数),出现传输极点,传输最有利: 当(W2+1)/t=(2+1)kz时,出现传输零点,传输衰耗最大。 39题图3.3所示的传号和空号相间的数字信号通过某随参信道。己知接收信号是通过该信 道两条路径的信号之和。设两径的传输衰减相等(均为),且时延差t=T4。试画出接收 信号的波形示意图 解: 题图3.3 T 2T 3T t OI T 第19页
《通信原理》第三章 信道 习题 第19页 解:对(a) H(ω)=R2/(R1+R2) ∣H(ω)∣= R2/(R1+R2) td(ω) φ(ω)=0 td(ω)=- dφ(ω)/dω =0 ω ∴信号通过该信道时无群迟延失真。 对(b) H(ω)=1/(1+jωRC) ∣H(ω)∣= 1/√1+ω2R 2C 2 φ(ω)=-arctg(ωRC) td(ω)=- dφ(ω)/dω =RC/(1+ω2R 2C 2 ) ∴信号通过该信道时有群迟延失真。 3-8 假设某随参信道的两径时延差为 1ms,试求该信道在哪些频率上传输衰耗最大?所传输 的信号选用哪些频率传输最有利? 解:τ=1ms 当 f=n/τ=n kHz 时(n 为整数),出现传输极点,传输最有利; 当 f=(n/2+1)/τ=(n/2+1)kHz 时,出现传输零点,传输衰耗最大。 3-9 题图 3.3 所示的传号和空号相间的数字信号通过某随参信道。已知接收信号是通过该信 道两条路径的信号之和。设两径的传输衰减相等(均为 d),且时延差τ=T/4。试画出接收 信号的波形示意图。 解: S(t) 题图 3.3 O T 2T 3T t O τ T t

《通信原理》第三章信道习趣 3-10若两个电阻的阻值都为1000Q,它们的温度分别为300K和400K,试求这两个电阻串 联后两端的噪声功率谱密度。 解:S1(o)=2KTR=2×1.38×1023×300×1000=8.28×1018V2/Hz S2()=2×1.38×1023×400×1000=11.04×1018V/H2 S(w)=S1(u)+S2(u)=19.32×1018V2/H 3-11设高斯信道的带宽为4kH2,信号与噪声的功率比为63,试确定利用这种信道的理想通 信系统之传信率和差错率 解:B-4kHz,SN-63 C=B log 2(l+S/N)=4k bog 2(1+63)=24kb/s 对理想通信系统,其传信率达到最大值,即 传信率=24kb/s,差错率-0 3-12某一待传输的图片约含2.25×105个像元。为了很好地重现图片需要12个亮度电平。 假若所有这些亮度电平等概率出现,试计算用3min传送一张图片时所需的信道带宽(设信 道中信噪功率比为30B)。解:每像元信息量=-g:(1/12)≈3.58bit 图片包含信息量=3.58×2.25×10的≈8.06×10bit 要在3min内传送一张图片时,C=8.06×10P/180≈4.48×10bits S/N=30dB-=100w10=1000 B=C/log 2(1+S/N)4.49X10 Hz 第20项
《通信原理》第三章 信道 习题 第20页 3-10 若两个电阻的阻值都为 1000Ω,它们的温度分别为 300K 和 400K,试求这两个电阻串 联后两端的噪声功率谱密度。 解:S1(ω)=2KTR=2×1.38×10-23×300×1000=8.28×10-18 V2∕Hz S2(ω)=2×1.38×10-23×400×1000=11.04×10-18 V2∕Hz S(ω)= S1(ω)+ S2(ω)=19.32×10-18 V2∕Hz 3-11 设高斯信道的带宽为 4kHz,信号与噪声的功率比为 63,试确定利用这种信道的理想通 信系统之传信率和差错率。 解:B=4kHz, S/N=63 C=B ㏒ 2(1+S/N)=4k ㏒ 2(1+63)=24kb/s 对理想通信系统,其传信率达到最大值,即 传信率=24kb/s,差错率=0 3-12 某一待传输的图片约含 2.25×106 个像元。为了很好地重现图片需要 12 个亮度电平。 假若所有这些亮度电平等概率出现,试计算用 3min 传送一张图片时所需的信道带宽 (设信 道中信噪功率比为 30dB)。解:每像元信息量=-㏒ 2(1/12)≈3.58 bit 图片包含信息量=3.58×2.25×106≈8.06×106 bit 要在 3min 内传送一张图片时,C=8.06×106 /180≈4.48×104 bit/s S/N=30dB=1030/10=1000 B=C/㏒ 2(1+S/N)≈4.49×103 Hz