石河子大学：《通信原理》课程教学资源（习题解答）第四章 模拟调制系统

《通信原理》第四章模拟调制系统习题 第四章模拟调制系统习题(30道) 1.已知调制信号m()=Cos(2000rt)+c0s(4000a),载波为cos104rt,进行单边带调制， 试确定该单边带信号的表达试，并画出频谱图。 解：方法一：若要确定单边带信号，须先求得m()的希尔伯特变换 m(t)=c0s(2000/2)+cos(4000t/2) =sin (2000)+sin (4000) 故上边带信号为 SUSB(t)=1/2m(t)coswc-1/2m(t)sinwcl =1/2cog12000xt)r1/2cog14000rt) 下边带信号为 SLSB(t)=1/2m(t)coSWc+1/2m(t)sim =1/2c0s8000rt+1/2cos6000z0 其频谱如图所示。 2 SUSB (L 1400-1200 1600 6000x8000 方法二：先产生DSB信号：m)m()coswc=,然后经过边带滤波器，产生SSB信号。 2,将调幅波通过残留边带滤波器产生残留边带信号。若次信号的传输函数H()如图所示 当调制信号为m()=A[sin100t+sin6000时，试确定所得残留边带信号的表达式。 解：设调幅波sm()=[0m(t)]coswct,0≥m()ax,且sn()Sm() H(w) ☐ 14-10595 根据残留边带滤波器在￡。处具有互补对称特性，从Hw)图上可知载频。=10kz,因此得载 波cos20000夏t。故有 第22项

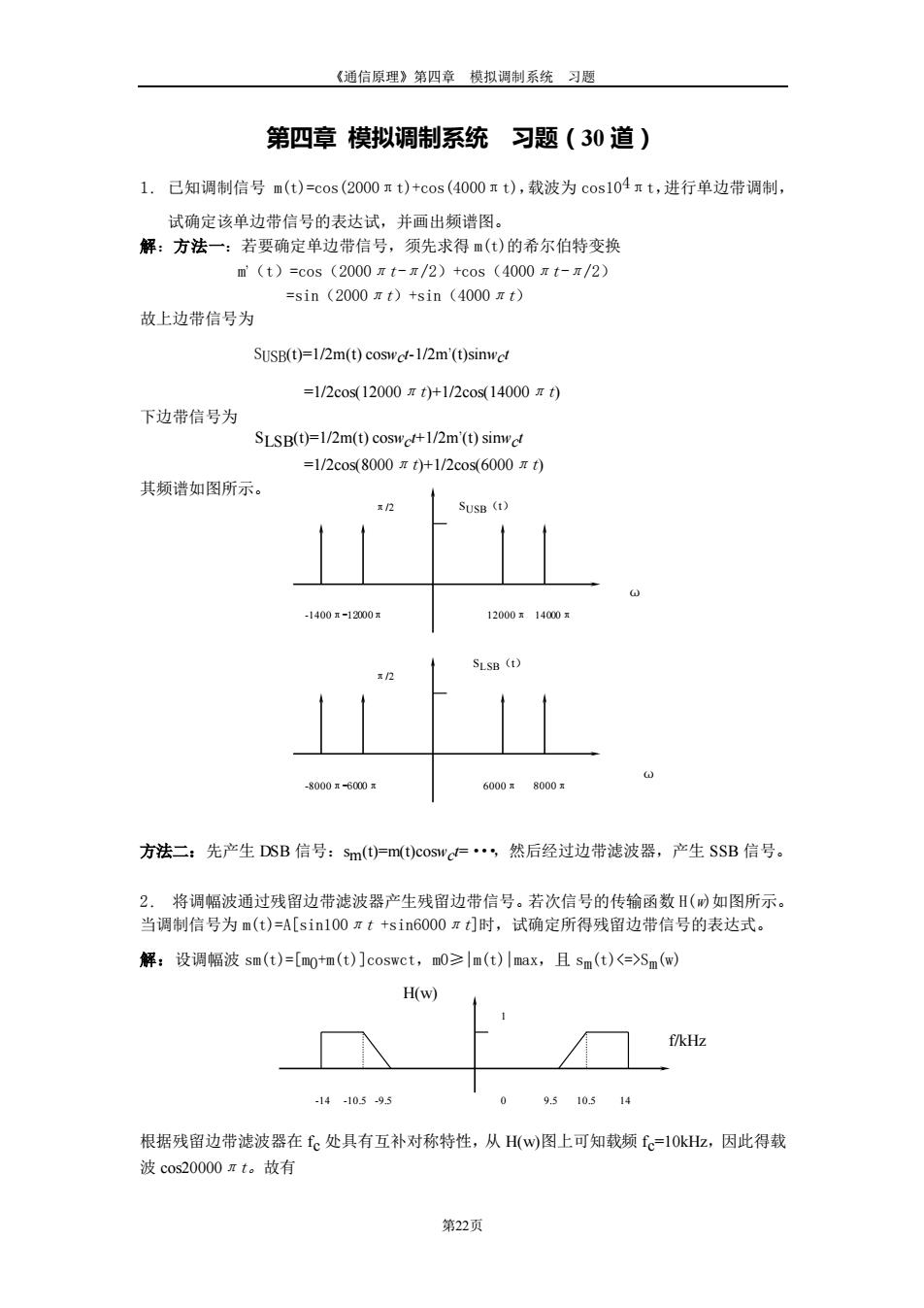
《通信原理》第四章 模拟调制系统 习题 第22页 第四章 模拟调制系统 习题（30 道） 1. 已知调制信号 m(t)=cos(2000πt)+cos(4000πt)，载波为 cos104πt，进行单边带调制， 试确定该单边带信号的表达试，并画出频谱图。 解：方法一：若要确定单边带信号，须先求得 m(t)的希尔伯特变换 m’（t）=cos（2000πt-π/2）+cos（4000πt-π/2） =sin（2000πt）+sin（4000πt） 故上边带信号为 SUSB(t)=1/2m(t) coswct-1/2m’(t)sinwct =1/2cos(12000πt)+1/2cos(14000πt) 下边带信号为 SLSB(t)=1/2m(t) coswct+1/2m’(t) sinwct =1/2cos(8000πt)+1/2cos(6000πt) 其频谱如图所示。 方法二：先产生 DSB 信号：sm(t)=m(t)coswct=···，然后经过边带滤波器，产生 SSB 信号。 2. 将调幅波通过残留边带滤波器产生残留边带信号。若次信号的传输函数 H(w)如图所示。 当调制信号为 m(t)=A[sin100πt +sin6000πt]时，试确定所得残留边带信号的表达式。 解：设调幅波 sm(t)=[m0+m(t)]coswct，m0≥|m(t)|max，且 sm(t)Sm(w) 根据残留边带滤波器在 fc 处具有互补对称特性，从 H(w)图上可知载频 fc=10kHz，因此得载 波 cos20000πt。故有 ω -1400π-12000π 12000π 14000π π/2 SUSB（t） ω π/2 SLSB（t） -8000π-6000π 6000π 8000π 1 -14 -10.5 -9.5 9.5 10.5 14 f/kHz H(w) 0

《通信原理》第四章模拟调制系统习题 sm(t)=[mg+m(t)]cos20000 =m0cos200007t+A/2[sin(20100It)-sin(19900nt) +sin(26000Tt》-sin(14000rt月 Sm(w)=xm0[o -0(w+14000r)+0(w-14000r) 残留边带信号为下(t),且f(t)F(w),则下()=Sm(w)H() 故有： F()=/2m0[o(w+20000r)+0(-20000r)]+jA/2[0.550(+20100r) -0.550(w-20100r)-0.450(x+19900r)+0.450(w-19900r)+o(w+26000r) 0(国-26000r） ft1/2m0cos20000rt+A/2[0.55sin20100Tt-0.45sinl19900rt+sin26000rt] 3.设某信道具有均匀的双边噪声功率谱密度P(0-0.5*103W/Hz,在该信道中传输抑制载 波的双边带信号，并设调制信号m()的频带限制在5kz,而载波为100k业，已调信号的功 率为1OkW若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器滤波，试问： (1)该理想带通滤波器应具有怎样的传输特性H(w)? (2)解调器输入端的信噪功率比为名少？ (3)解调器输出端的信噪功率比为多少？ (4)求出解调器输出端的噪声功率谱密度，并用图型表示出来 (1)为了保证信号顺利通过和尽可能的滤除噪声，带通滤波器的宽度等于已调信号带宽， 即B=2fm=2*5=10kHz,其中中心频率为100kHz。所以 H(w=K,95kz≤|f|≤105kz 0 ,其他 (2)Si=10kW Ni=2B*Pn(0-=2*10*103*0.5*103=10W 故输入信噪比SiN=1000 (3)因右GDsB=) 故输出信噪比S0N0=200( (4)据双边带解调器的输出嘈声与输出嘈声功率关系，有： N0=1/4Ni=2.5W 故Pm双(0=N0/2fm=0.25*103w/z =12Pm(01f1≤5kH2 第23页

《通信原理》第四章 模拟调制系统 习题 第23页 sm(t)=[m0+m(t)]cos20000πt =m0cos20000πt+A[sin100πt+sin6000πt]cos20000πt =m0cos20000πt+A/2[sin(20100πt)-sin(19900πt) +sin(26000πt)-sin(14000πt) Sm(w)=πm0[σ(w+20000π)+σ(W-20000π)]+jπA/2[σ(w+20100π)- σ(w+19900π)+σ(w-19900π)+σ(w+26000π)-σ(w-26000π) -σ(w+14000π)+σ(w-14000π) 残留边带信号为 F(t)，且 f(t)F(w)，则 F(w)=Sm(w)H(w) 故有： F(w)=π/2m0[σ(w+20000π)+σ(w-20000π)]+jπA/2[0.55σ(w+20100π) -0.55σ(w-20100π)-0.45σ(w+19900π)+ 0.45σ(w-19900π)+σ(w+26000π) -σ(w-26000π) f(t)=1/2m0cos20000πt+A/2[0.55sin20100πt-0.45sin19900πt+sin26000πt] 3. 设某信道具有均匀的双边噪声功率谱密度 Pn(f)=0.5*10-3W/Hz，在该信道中传输抑制载 波的双边带信号，并设调制信号 m(t)的频带限制在 5kHz，而载波为 100kHz，已调信号的功 率为 10kW.若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器滤波，试问： （1）该理想带通滤波器应具有怎样的传输特性 H(w)? （2）解调器输入端的信噪功率比为多少? （3）解调器输出端的信噪功率比为多少? （4）求出解调器输出端的噪声功率谱密度，并用图型表示出来。 解： （1）为了保证信号顺利通过和尽可能的滤除噪声，带通滤波器的宽度等于已调信号带宽， 即 B=2fm=2*5=10kHz，其中中心频率为 100kHz。所以 H(w)=K ，95kHz≤∣f∣≤105kHz 0 ，其他 （2）Si=10kW Ni=2B* Pn(f)=2*10*103 *0.5*10-3 =10W 故输入信噪比 Si/Ni=1000 （3）因有 GDSB=2 故输出信噪比 S0/N0=2000 （4）据双边带解调器的输出嘈声与输出嘈声功率关系，有： N0=1/4 Ni =2.5W 故 Pn 双(f)= N0/2fm=0.25*10-3W/Hz =1/2 Pn(f) ∣f∣≤5kHz

《通信原理》第四章模拟调制系统习题 Pn([XW/HZ) 0.2510 -5 0 5 f/kHz 4.若对某一信号用DSB进行传输，设加至接收机的调制信号m()的功率谱密度为 Pm(f)=nm/2*|f l/fm,Ifl fm 0 1fl≥m 试求： (1)接受机的输入信号功率 (2)接收机的输出信号功率 (3)若叠加于DSB信号的白噪声具有双边功率谱密度为0/2，设解调器的输出端接有 截止频率为m的理想低通滤波器，那么输出信躁功率比为多少？ 解：(1)设双边带信号sm(t-m()coswet,则输入信号功率 Si=s2m (t)=1/2 m2(t)=1/4 fm*nm (2)双边带信号采用相干解调的输出为m0(0=1/2m(0,故输出信号功率 S0=m20t)=14m2(0)1/8fim*nm 3)因Ni=n0B,B-2fm,则N0=1/4Ni=1/4·n0B=/2·n0fm 故输出信噪比 S0/N0=1/4·nm/n0 5。设某信道具有均匀的双边噪声功率谱密度Pm()=5*103/恤，在该信道中传输抑制载 波的单边带信号，并设调制信号m(t)的频带限制在5kz。而载频是100kz,已调信号功 率是10k。若接收机的输入信号在加至解调器之前，先经过 理想带通滤波器，试问： (1) 该理想带通滤波器应具有怎样的传输特性 (2)解调器输入端信躁比为多少？ (3)解调器输出端信噪比为多少？ 解：(1)H(f)=k,100kHz≤|f|≤105kz =0 其他 (2)Ni=Pm(0)·2fm=0.5*103*2*5*103=5W 故Si/Ni=10*103/5=2000 (3)因有Gs=l,Sa/N0=5;/N:=2000 6。某线性调制系统的输出信噪比为20B,输出噪声功率为109，由发射机输出端到调制 器输入端之间总的传输耗损为100B,试求： (1)DSB/SC时的发射机输出功率。 (2)SSB/SC时的发射机输出功率。 第24项

《通信原理》第四章 模拟调制系统 习题 第24页 4. 若对某一信号用 DSB 进行传输，设加至接收机的调制信号 m(t)的功率谱密度为 Pm(f)= nm/2*│f│/fm ， │f│≤fm 0 │f│≥fm 试求： （1） 接受机的输入信号功率 （2） 接收机的输出信号功率 （3） 若叠加于 DSB 信号的白噪声具有双边功率谱密度为 n0/2，设解调器的输出端接有 截止频率为 fm 的理想低通滤波器，那么输出信噪功率比为多少? 解：（1）设双边带信号 sm(t)=m(t)coswct，则输入信号功率 Si=s2m (t)=1/2 m 2 (t)=1/4 fm*nm （2）双边带信号采用相干解调的输出为 m0(t)=1/2m(t)，故输出信号功率 S0=m2 0(t)=1/4 m 2 (t)=1/8 fm*nm 3）因 Ni=n0B，B=2fm，则 N0=1/4Ni=1/4·n0B=1/2·n0fm 故输出信噪比 S0/N0=1/4·nm/n0 5. 设某信道具有均匀的双边噪声功率谱密度 Pn（f）=5*10-3 W/Hz，在该信道中传输抑制载 波的单边带信号，并设调制信号 m（t）的频带限制在 5kHz。而载频是 100kHz，已调信号功 率是 10kW。若接收机的输入信号在加至解调器之前，先经过一理想带通滤波器，试问： （1） 该理想带通滤波器应具有怎样的传输特性。 （2） 解调器输入端信噪比为多少? （3） 解调器输出端信噪比为多少? 解：（1）H(f)= k ，100kHz≤∣f∣≤105kHz = 0 ， 其他 （2）Ni=Pn(f)·2fm=0.5*10-3 *2*5*103 =5W 故 Si/Ni=10*103 /5=2000 （3）因有 GSSB=1， S0/N0= Si/Ni =2000 6. 某线性调制系统的输出信噪比为 20dB，输出噪声功率为 10-9 W，由发射机输出端到调制 器输入端之间总的传输耗损为 100dB，试求： （1） DSB/SC 时的发射机输出功率。 （2） SSB/SC 时的发射机输出功率。 Pn(f)(W/Hz) 0.25*10-3 -5 0 5 f/kHz

《通信原理》第四章模拟调制系统习题 解：设发射机输出功率为ST,损耗K=ST/Si=1010(100dB),已知S0N0=100·(20dB) N0=109 (1) DSB/SC方式： 因为G=2, SiNi=1/2·S0/N0=50 又因为Ni=4NO Si=50Ni=200N0=2#10/W ST=K·Si=2*103w (2) SSB/SC方式 因为G=1, Si/Ni=S0/NO=100 又因为Ni=4N0 Si=100Ni=400N0=4*10-7W ST=K·Sie4*103w 7.试证明：当M信号采用同步检测法进行解调时，其制度增益G与公式(4-37)的结果相 证明：设AM信号为 sm(t)=[A+m(t)]coswet 式中，A≥|m(t)|ax输入噪声为 ni(t)=nc(t)coswct-ns(t)sinwct 则解调器输入的信号功率Si和噪声功率N分别为 Si=A2/2+m2()/2,Ni=n2i(t)=n0B 设同步检测（相干解调）中，相干载波为coswct,.则 [sm(t)+ni(t)]coswct 士将 m(t)/2+nc(t) 故输出有用信号和输出噪声分别为 0(t)=m(t)/2, n0(t)=nc(t)/2 所以 S0=m2(t)/4,N0=n2c(t)/4=n0B/4 故： G=2m2()/[a2+m2(0] 8.设某信道具有均匀的双边噪声功率谱密度Pm(f)=0.5*103/z,在该信道中传输振幅调 制信号，并设调制信号m(t)的频带限制在5kz,而且载频是100kz,边带功率为10k,载 波功率为4k。若接收机的输入信号先经过一个合适的理想带通滤波器，然后再加至包络 检波器进行调制。试求： 第25页

《通信原理》第四章 模拟调制系统 习题 第25页 解：设发射机输出功率为 ST，损耗 K=ST/Si=1010(100dB)，已知 S0/N0=100·（20dB）， N0=10-9 W （1） DSB/SC 方式： 因为 G=2， Si/Ni=1/2·S0/N0=50 又因为 Ni=4N0 Si=50Ni=200N0=2*10-7W ST=K·Si=2*103W （2） SSB/SC 方式： 因为 G=1， Si/Ni= S0/N0=100 又因为 Ni=4N0 Si=100Ni=400N0=4*10-7W ST=K·Si=4*103W 7. 试证明：当 AM 信号采用同步检测法进行解调时，其制度增益 G 与公式 (4-37)的结果相 同。 证明：设 AM 信号为 sm(t)=[A+m(t)]coswct 式中，A≥∣m(t)∣max 输入噪声为 ni(t)=nc(t)coswct-ns(t)sinwct 则解调器输入的信号功率 Si 和噪声功率 Ni 分别为 Si=A2 /2+m2 (t)/2，Ni=n2 i(t)=n0B 设同步检测(相干解调)中，相干载波为 coswct，则 [sm(t)+ni(t)]coswct LPF A/2+m(t)/2+nc(t) 故输出有用信号和输出噪声分别为 m0(t)=m(t)/2， n0(t)=nc(t)/2 所以 S0=m2 (t)/4， N0=n2 c(t)/4=n0B/4 故： G=2m2 (t)/[A2 +m2 (t)] 8. 设某信道具有均匀的双边噪声功率谱密度 Pn(f)=0.5*10-3 W/Hz，在该信道中传输振幅调 制信号，并设调制信号 m(t)的频带限制在 5kHz，而且载频是 100kHz，边带功率为 10kW，载 波功率为 40kW。若接收机的输入信号先经过一个合适的理想带通滤波器，然后再加至包络 检波器进行调制。试求：

《通信原理》第四章模拟调制系统习题 (1)解调器输入端的信噪功率比 (2)解调器输出端的信噪功率比 (3)制度增益 解：(1).设sAMt)=A+m(t)]coswet,.且m(t)=0,则 Si=1/2A2+1/2m2(t)=Pe+Ps-50kW 式中，Pc为载波功率，Ps为边带功率 Ni=Pn0·2B=Pm(0·4im=10 故 S./N,=5000(37dB) (2)假定[A+m(t)]>nit),则理想包络检波输出为 E)≈A+m()+nc0则：S0=m2()-2Ps-2*10=20kW:N0=n2ct)=Ni=10kW 故SN0=2000(33dB (3)G=2000/5000=25 9.己知某单频调频波的振幅是10Y,瞬时频率为f(t)=105+10c0s2夏*103tz,试求： (1)此调频波的表达式 解： (1)该调制博得瞬时角频率为 wt0=2f()=2*105+2*10cos2*103rad/S 此时，该调频波的总相位 0(t)=∫w(T)dt=2π*105t+10sin2r*103t 因此，调频波的时域表达式sF(t)为 sFM(t)=Acos0(t)=20cos(2*105t+10sin2103t)V (2)根据频率偏移的定义 △f=1△f(t)|MAX=1104cos2T*103t|MAK=10kHz 调频指数为 mf=△f/frF104/103=10 这样可以得到调频波的带宽为 B≈2（△f+fm)=2(10+1)=22kHz (3)现调制信号频率fm由103z提高到2*10z。因须率调制时己调波频率偏移与 调制信号频率无关，故这时调频信号的频率偏移仍然是 △f=10kH2 而这时调频指数变为 mf=△f/fm=104/2*103-5 第26页

《通信原理》第四章 模拟调制系统 习题 第26页 （1） 解调器输入端的信噪功率比 （2） 解调器输出端的信噪功率比 （3） 制度增益 G 解：（1）.设 sAM(t)=[A+m(t)]coswct，且 m(t)=0，则 Si=1/2A2 +1/2m2 (t)=Pc+Ps=50kW 式中， Pc 为载波功率， Ps 为边带功率 又 Ni=Pn(f)·2B= Pn(f)·4fm=10W 故 Si/Ni=5000（37dB） （2）假定[A+m（t）]>>ni(t)，则理想包络检波输出为 E(t)≈A+m(t)+nc(t) 则：S0=m2 (t)=2Ps=2*10=20kW；N0=n 2 c(t)=Ni=10kW 故 S0/N0=2000(33dB) （3）G=2000/5000=2/5 9. 已知某单频调频波的振幅是 10V，瞬时频率为 f(t)=106 +10 4 cos2π*103 tHz，试求： （1）此调频波的表达式 （2）此调频波的频率偏移，调频指数和频带宽度 （3）调制信号频率提高到 2*103 Hz，则调频波的频偏，调制指数和频带宽度如何变化? 解： （1）该调制博得瞬时角频率为 w(t)=2πf(t)=2π*106 +2π*104 cos2π*103 t rad/s 此时，该调频波的总相位 θ(t)=∫w(τ)dτ=2π*106 t+10sin2π*103 t 因此，调频波的时域表达式 sFM(t)为 sFM(t)=Acosθ(t)=20cos(2π*106 t+10sin2π103 t)V （2）根据频率偏移的定义 Δf=∣Δf(t)∣MAX=∣104 cos2π*103 t∣MAX=10kHz 调频指数为 mf=Δf/fm=104 /103 =10 这样可以得到调频波的带宽为 B≈2(Δf+fm)=2(10+1)=22kHz （3） 现调制信号频率 fm 由 103 Hz 提高到 2*103 Hz。因频率调制时已调波频率偏移与 调制信号频率无关，故这时调频信号的频率偏移仍然是 Δf=10kHz 而这时调频指数变为 mf=Δf/fm=104 /2*103 =5

《通信原理》第四章模拟调制系统习题 这时调频信号的带宽为 B≈2(Af+fm)=2(10+2)=24kH2 由上述结果可知：由于△D>fm,所以，虽然调制信号频率fm增加了一倍，但调制 信号的带宽B变化很小。 10.根据图所示的调制信号波形，试画出DSB波形 M(t) M(t 11.根据上题所求出的DSB图形，结合书上的AM波形图，比较它们分别通过包络检波器 后的波形差别 解：讨论比较：DSB信号通过包络检波器后产生的解调信号已经严重失真，所以DSB信号 不能采用包络检波法：而AM可采用此法恢复m()。 12.某调制方框图如下，已知m(t)的频谱如下面所示。载频1，且理想低通滤 波器的截止频率为w1,试求输出信号s(),并说明s()为何种一调制信号。 M(w) 西人 理想低通 解：sl()-m()cosw1 tcosw2t s2(t)=m(t)sinwltsinw2t 第27页

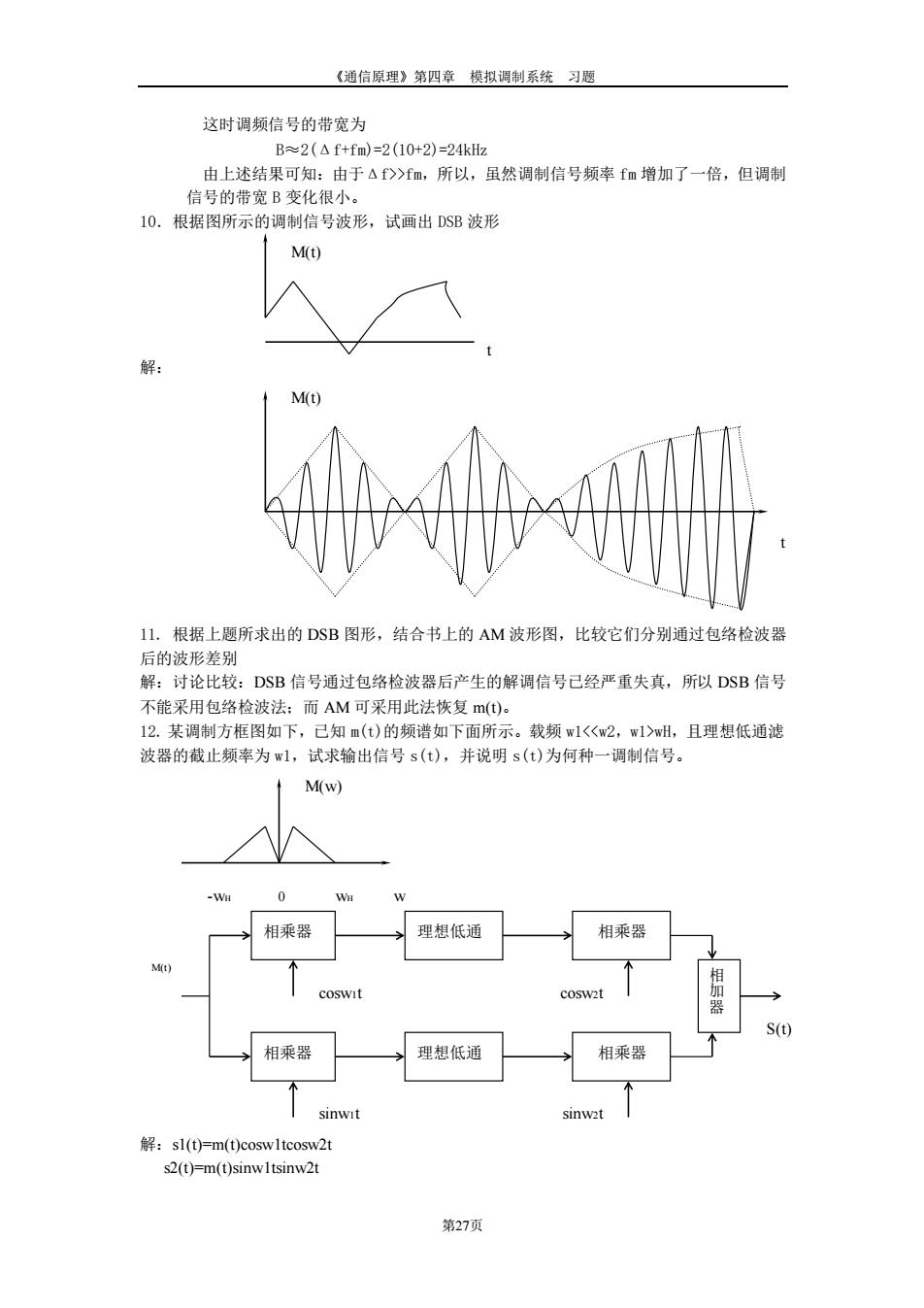
《通信原理》第四章 模拟调制系统 习题 第27页 这时调频信号的带宽为 B≈2(Δf+fm)=2(10+2)=24kHz 由上述结果可知：由于Δf>>fm，所以，虽然调制信号频率 fm 增加了一倍，但调制 信号的带宽 B 变化很小。 10．根据图所示的调制信号波形，试画出 DSB 波形 解： 11. 根据上题所求出的 DSB 图形，结合书上的 AM 波形图，比较它们分别通过包络检波器 后的波形差别 解：讨论比较：DSB 信号通过包络检波器后产生的解调信号已经严重失真，所以 DSB 信号 不能采用包络检波法；而 AM 可采用此法恢复 m(t)。 12. 某调制方框图如下，已知 m(t)的频谱如下面所示。载频 w1wH，且理想低通滤 波器的截止频率为 w1，试求输出信号 s(t)，并说明 s(t)为何种一调制信号。 解：s1(t)=m(t)cosw1tcosw2t s2(t)=m(t)sinw1tsinw2t t M(t) M(w) -wH 0 wH w 相乘器 理想低通 相乘器 相乘器 理想低通 相乘器 相 加 器 M(t) cosw1t sinw1t cosw2t sinw2t S(t) t M(t)

《通信原理》第四章模拟调制系统习题 经过相加器后所得的s)即为： Fs1(0+s20 =m(t)[coswlcosw2+sinwlsinw2] =m(t)cos[(wl-w2)t] 由已知wlwH 故： s(t)-m(t)cosw2t 所以所得信号为DSB信号 13.已知调制信号的频谱图如图所示，载波为cos104πt,试确定该信号的单边带信号表达 式，并求出该调制信号。 SusB(t) /4 -13000复-11000m0 11000113000第 SLsB(t) /4 -9000x-7000r07000算9000开 解：由已知的图即可得知： 上边带信号为 SUSB(t)=1/4m(t)coswc-1/4m(t)simcl =1/4cos(13000xt+1/4cos11000z) 下边带信号为 SLSB(t)=1/4m(t)coswc+1/4m(t) =1/4cos(9000rt)+1/4cos7000πt) 因此可以求得m(t)的希尔伯特变换 m(t)=sin (1000t)+sin (3000t) =cos(1000rt-T/2)+cos(3000TtF/2) 这样即可求得调制信号 m(t)=cos(1000t)+cos(3000t) 14.己知调制信号的上边带信号为SUSB(t1/4cos(25000万+1/4co(22000t),已知该载波 为c0s2*104t求该调制信号的表达式， 第28页

《通信原理》第四章 模拟调制系统 习题 第28页 经过相加器后所得的 s(t)即为： s(t)=s1(t)+s2(t) =m(t)[cosw1cosw2+sinw1sinw2] =m(t)cos[(w1-w2)t] 由已知 w1wH 故： s(t)=m(t)cosw2t 所以所得信号为 DSB 信号 13. 已知调制信号的频谱图如图所示， 载波为 cos104πt，试确定该信号的单边带信号表达 式，并求出该调制信号。 解：由已知的图即可得知： 上边带信号为 SUSB(t)=1/4m(t) coswct-1/4m’(t)sinwct =1/4cos(13000πt)+1/4cos(11000πt) 下边带信号为 SLSB(t)=1/4m(t) coswct+1/4m’(t) sinwct =1/4cos(9000πt)+1/4cos(7000πt) 因此可以求得 m(t)的希尔伯特变换 m’（t）=sin（1000πt）+sin（3000πt） =cos（1000πt-π/2）+cos（3000πt-π/2） 这样即可求得调制信号 m(t)=cos(1000πt)+cos(3000πt) 14. 已知调制信号的上边带信号为 SUSB(t)=1/4cos(25000πt)+1/4cos(22000πt)，已知该载波 为 cos2*104πt 求该调制信号的表达式。 SUSB(t) w -13000π -11000π 0 11000π13000π π/4 SLSB(t) π/4 w -9000π-7000π 0 7000π 9000π

《通信原理》第四章模拟调制系统习题 解：由己知的上边带信号表达式SUS()即可得出该调制信号的下边带信号表达式 SLSB(t)=1/4cos(18000)+1/4co(15000) 有了该信号两个边带表达式，利用上一例题的求解方法，求得 m(t)=cos (2000 t)+cos(5000t) 15.将调幅波通过残留边带法波婴产生武留功带信号。立生的或边带信号麦达式如下 ft0=1/2 0cos100001t+/2[0.5sin10100年t-0.45sin9900元t+sin16000t,我波为 cos10000t。而且已经知道调制信号的表达式为m(t)=A[sin100t+sin6000 试画出该信号的传输函数H(W)。 解：由已知产生的残边带信号表达式f(t)可以知道： F()=T/2m0[0(w+10000x)+o(w-10000π)]+jπA/2[0.550(+10100E）) -0.55(-10100)-0.450(m+9900)+0.45(9900)+(m+16000m） 0(w-16000r) 由已知的m(t)可以得出： Sm(w)=πm0[0(+10000万)+o(W-10000)]+jTA/2[o(w+10100x） 0(g+9900x)+0(w-9900r)+g(+16000立)-0(w-16000r) -0(+4000)+0(-4000) (详细做法参厢习题2) 这样H(w)=F()/Sm(w)）即可画出传输函数H(国)。 (图略，与二的H()图相似) 16.设某信道具有均匀的双边噪声功率谱密度P(①，在该信逍中传输抑制载波的双边带信 号，并设调制信号m)的频带限制在10kz,而载波为250kHz, 已调信号的功率为15kW 己知解调器输入端的信噪功率比为1000。若接收机的输入信号在加至解调器之前，先经过 想带通滤波器滤波，求双边噪声功率谱密度P(). 解 输入信躁比Si/Ni=1000 Si=15kW Ni=2B*Pn(0=2*15*103◆Pn(0=15W 故求得Pnf=0.5*10°W/Hz 17,假设上题己知的为解调器输出端的信噪比，再求双边噪声功率谱密度P()。 解：GDSB=2 故输出信噪比 So/No=2Si/Ni=1000 所以SN,=500 由上一例题即可求得：Pn0=1*10~3w/ 18.某线性调制系统的输出信噪比为20B,输出噪声功率为108，DSB/SC时的发射机输 出功率为2*10试求：从输出端到解调输入端之间总的传输损耗留 第29页

《通信原理》第四章 模拟调制系统 习题 第29页 解： 由已知的上边带信号表达式 SUSB(t)即可得出该调制信号的下边带信号表达式： SLSB(t)=1/4cos(18000πt)+1/4cos(15000πt) 有了该信号两个边带表达式，利用上一例题的求解方法，求得 m(t)=cos(2000πt)+cos(5000πt) 15. 将调幅波通过残留边带滤波器产生残留边带信号。产生的残边带信号表达式如下 f(t)=1/2m0cos10000πt+A/2[0.55sin10100πt-0.45sin9900πt+sin16000πt]，载波为 cos10000πt。而且已经知道调制信号的表达式为 m(t)=A[sin100πt +sin6000πt] 试画出该信号的传输函数 H(w)。 解：由已知产生的残边带信号表达式 f(t)可以知道： F(w)=π/2m0[σ(w+10000π)+σ(w-10000π)]+jπA/2[0.55σ(w+10100π) -0.55σ(w-10100π)-0.45σ(w+9900π)+ 0.45σ(w-9900π)+σ(w+16000π) -σ(w-16000π) 由已知的 m(t)可以得出： Sm(w)=πm0[σ(w+10000π)+σ(W-10000π)]+jπA/2[σ(w+10100π)- σ(w+9900π)+σ(w-9900π)+σ(w+16000π)-σ(w-16000π) -σ(w+4000π)+σ(w-4000π) (详细做法参照习题２) 这样 H(w)=F(w)/ Sm(w) 即可画出传输函数 H(w)。 (图略，与二的 H(w)图相似) 16. 设某信道具有均匀的双边噪声功率谱密度 Pn(f)，在该信道中传输抑制载波的双边带信 号，并设调制信号 m(t)的频带限制在 10kHz，而载波为 250kHz，已调信号的功率为 15kW。 已知解调器输入端的信噪功率比为 1000。若接收机的输入信号在加至解调器之前，先经过 一理想带通滤波器滤波，求双边噪声功率谱密度 Pn(f)。 解： 输入信噪比 Si/Ni=1000 Si=15kW Ni=2B* Pn(f)=2*15*103 * Pn(f)=15W 故求得 Pn(f)=0.5*10-3W/Hz 17. 假设上题已知的为解调器输出端的信噪比，再求双边噪声功率谱密度 Pn(f)。 解： GDSB=2 故输出信噪比 S0/N0=2Si/Ni=1000 所以 Si/Ni=500 由上一例题即可求得：Pn(f)=1*10-3W/Hz 18. 某线性调制系统的输出信噪比为 20dB，输出噪声功率为 10-8 W， DSB/SC 时的发射机输 出功率为 2*103 W 试求：从输出端到解调输入端之间总的传输损耗?

《通信原理》第四章模拟调制系统习题 解：已知：输出噪声功率为N0=109 因为G=2 SiNi=12·S0N0=50 因为Ni=4No Si=50N,=200N0=2*10-6W 所以损耗K=ST/S,=109 19.将上一题的DSB/SC时的发射机输出功率改为SSB/SC时的发射机输出功率，再求：从输 出端到解调输入端之间总的传输损耗？ 解：因为G=1, Si/Ni=So/No=100 因为Ni=4N6,Si=100N=40ON0=4*106W 所以，损耗K=ST/5i=5*108 20.若对某一信号用SSB进行传输，设加至接收机的调制信号m()的功率谱密度为 Pm(f)=nm/2*I f l/fm, 1fl≥m 试求：接受机的输入信号功率。 解：设双单边带信号sm()m(t)coswct士1/2m'))sinwct,则输入信号功率 Si=s2m(t) =1/4[m(t)coswct-m'(t)sinwet2 =1/8 fm*nm 21.根据图所示的调制信号波形，试画出AM波形。 M(t) 解：AM波形如下所示 第30页

《通信原理》第四章 模拟调制系统 习题 第30页 解：已知： 输出噪声功率为 N0=10-9 W 因为 G=2， Si/Ni=1/2·S0/N0=50 因为 Ni=4N0 Si=50Ni=200N0=2*10-6W 所以 损耗 K=ST/Si=109 19. 将上一题的 DSB/SC 时的发射机输出功率改为 SSB/SC 时的发射机输出功率，再求：从输 出端到解调输入端之间总的传输损耗? 解： 因为 G=1， Si/Ni= S0/N0=100 因为 Ni=4N0，Si=100Ni=400N0=4*10-6W 所以，损耗 K=ST/Si=5*108 20. 若对某一信号用 SSB 进行传输，设加至接收机的调制信号 m(t)的功率谱密度为 Pm(f)= nm/2*│f│/fm ， │f│≤fm 0 │f│≥fm 试求：接受机的输入信号功率。 解：设双单边带信号 sm(t)=m(t)coswct±1/2m’(t)sinwct，则输入信号功率 Si=s2m (t) =1/4[m(t) coswct- m’(t)sinwct]2 =1/8 fm*nm 21. 根据图所示的调制信号波形，试画出 AM 波形。 解：AM 波形如下所示： M(t) t

《通信原理》第四章模拟调制系统习题 M(t) 22.根据图所示的调制信号波形，试画出DSB波形。试问DSB信号能不能采用包络检波法 M(t) M(t) DSB信号通过包络检波器后产生的解调信号已经严重失真，所似DSB信号不能采用包 络检波法 23.简述什么是载波调制？常见的调制有哪些？ 答：载波调制，就是按调制信号（基带信号）的变换规律去改变载波某些参数的过 第3引页

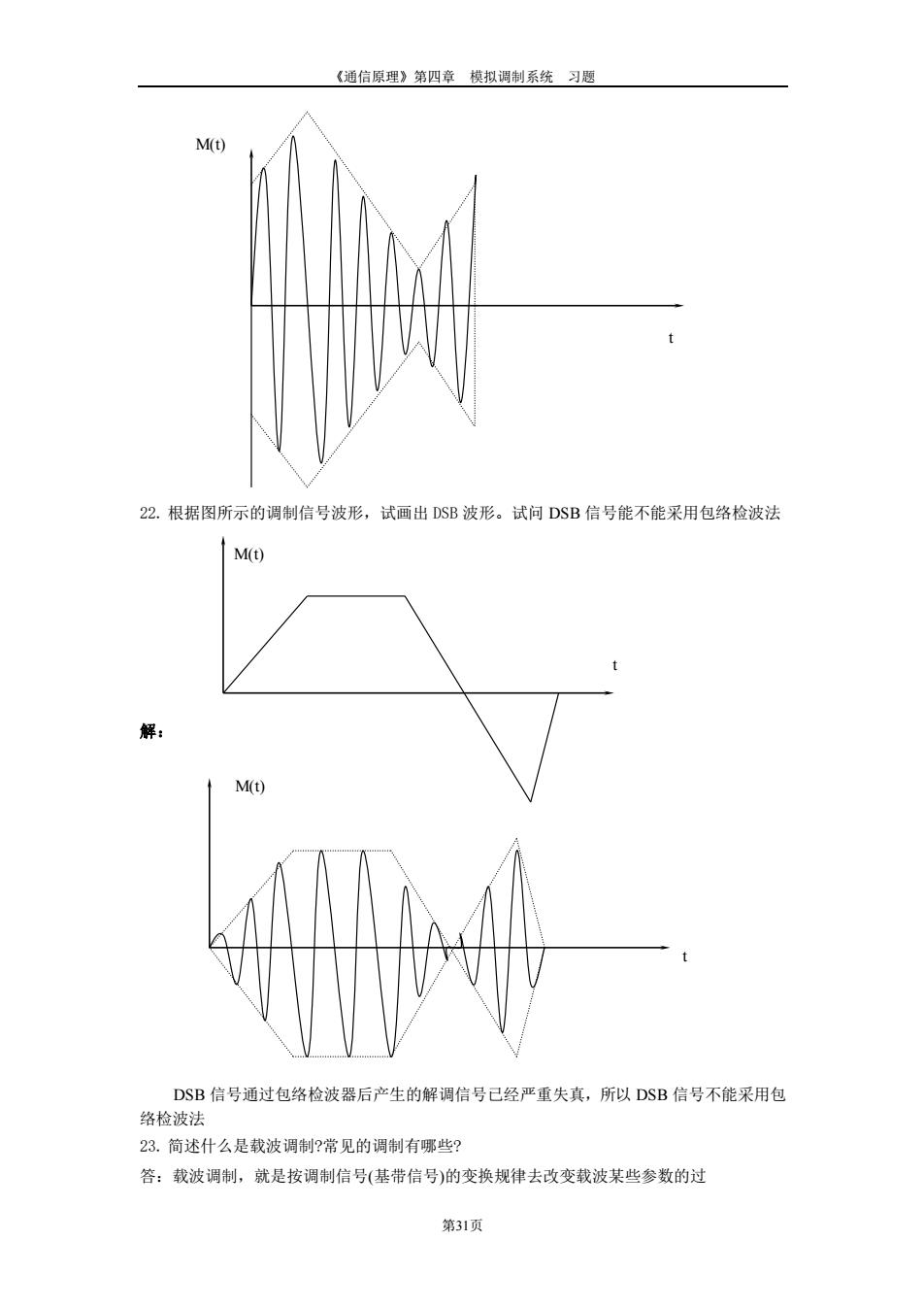
《通信原理》第四章 模拟调制系统 习题 第31页 22. 根据图所示的调制信号波形，试画出 DSB 波形。试问 DSB 信号能不能采用包络检波法 解： DSB 信号通过包络检波器后产生的解调信号已经严重失真，所以 DSB 信号不能采用包 络检波法 23. 简述什么是载波调制?常见的调制有哪些? 答：载波调制，就是按调制信号(基带信号)的变换规律去改变载波某些参数的过 M(t) t M(t) t t M(t)