
《通信原理》第五章数字基带传输系统习题 第五章数字基带传输系统习题(26道) 1,设随机二进制序列中的0和1分别由g)和-g(t)组成,它们的出现概率分别为P及(1-P) 求其功率谱密度及功率: 解:(1)随机二进制序列的双边功率谱密度为 Ps()=fsP(1-P)lG1(f)-G2(f)|2+Elfs[PG1(mfs)+(1-P)G2(mfs)]|28(f-mfs) 由g1(t)=-2(t)=g(t)得 Pd)=4fsP(1-P)G2(f)+fs(1-2P)2EIG(mfs)|28(f-mfs) 式中,G()是g(t)的频谱函数,在功率谱密度P()中,第一部分是其连续谱部分,第二部 分是其离散成分 随机二进制序列的功率为 S=1/2nP(ω)du -4fsP(1-P)fG2(F)df+lfs(1-2P)G(mfs)2(f-mfs)df =4fsP(1-P)JG2(f)df +fsP(1-P)2EIG(mfg)|2 (2②)当基带脉冲波形g(t)为 80=s 0,其他1 g)的傅立叶变换G(0为 an-r票 国为6n=x费-0 由题(1)中的结果知,此时的离散分量为0。 0,其他r g(t)的傅立叶变换G()为 工m对工2.+0 G0=2.12 π 所以该二进制序列存在离款分量广一号 第37页
《通信原理》第五章 数字基带传输系统 习题 第37页 第五章 数字基带传输系统 习题(26 道) 1. 设随机二进制序列中的 0 和 1 分别由 g(t)和-g(t)组成,它们的出现概率分别为 P 及(1-P): 求其功率谱密度及功率; 解:(1)随机二进制序列的双边功率谱密度为 Ps (ω)=fs P(1-P)|G1 (f)-G2 (f)|2 + ∑|fs [PG1 (mfs ) + (1-P)G2 (mfs )]|2δ(f- mfs ) 由 g1 (t)=-g2 (t)=g(t)得 Ps (ω)= 4fs P(1-P)G2(f) + fs (1-2P)2∑|G(mfs )| 2δ(f- mfs ) 式中,G(f)是 g(t)的频谱函数,在功率谱密度 Ps (ω)中,第一部分是其连续谱部分,第二部 分是其离散成分。 随机二进制序列的功率为 S=1/2л∫Ps (ω)dω =4fs P(1-P)∫G 2(f)df + ∑|fs (1-2P) G(mfs )| 2∫δ(f- mfs )df =4fs P(1-P)∫G 2(f)df + fs P(1-P)2∑|G(mfs )| 2 (2)当基带脉冲波形 g(t)为 = t T t g t s 0,其他 2 1,| | ( ) g(t)的傅立叶变换 G(f)为 s s s fT fT G f T sin ( ) = 因为 0 sin ( ) = = s s s s s f T f T G f T 由题(1)中的结果知,此时的离散分量为 0。 (3) = t T t g t s 0,其他 4 1,| | ( ) g(t)的傅立叶变换 G(f)为 0 / 2 sin / 2 2 ( ) = = s s s s s s T f T T f T G f 所以该二进制序列存在离散分量 s s T f 1 =

《通信原理》第五章数字基帝传输系统习题 2.设某二进制数字基带信号的基本脉冲为三角形脉冲,如图所示。图中T为码元间隔,数字 信号“1”和“0”分别用g)的有无表示,且“1”和“0”出现的概率相等: 7 (1)求该数字基带信号的功率谱密度,并画出功率谱密度图: (2)能否从该数字基带信中提取码元同步所需的频率人一乙的分量,若能,式计算该分量 的功率。 解:(1)对于单极性基带信号,g)=0,82()=g0),随机脉冲序列的功率谱密度为 p.(=fpl-p)G(Y|+∑/I-p)Gm'δf-m) 当p=2时 nn=4oUr+长cws-m) 由图可得 0,其他1 g()的傅立叶变换G()为 an=竖空) 代入功率谱密度函数式,得 a-m -g(空}2- 功率谱密度如图所示。 第38页
《通信原理》第五章 数字基带传输系统 习题 第38页 2. 设某二进制数字基带信号的基本脉冲为三角形脉冲,如图所示。图中 Ts 为码元间隔,数字 信号“1”和“0”分别用 g(t)的有无表示,且“1”和“0”出现的概率相等: (1) 求该数字基带信号的功率谱密度,并画出功率谱密度图; (2) 能否从该数字基带信中提取码元同步所需的频率 s s T f 1 = 的分量,若能,式计算该分量 的功率。 解:(1)对于单极性基带信号, ( ) 0, ( ) ( ) 1 2 g t = g t = g t ,随机脉冲序列的功率谱密度为 + =− = − + − − m s s s s mfs p ( f ) f p(1 p)G( f ) f (1 p)G(mf ) ( f ) 2 2 当 p=1/2 时 + =− = + − m s s s s s G mf f mf f G f f p f ( ) ( ) 4 ( ) 4 ( ) 2 2 由图可得 − = t T t t Ts A g t s 0,其他 2 ), 2 (1 ( ) g(t)的傅立叶变换 G(f)为 = 2 2 ( ) s 2 s fT Sa AT G f 代入功率谱密度函数式,得 ( ) + =− − + = m s s s s s s s s s f mf nf T Sa f T f AT Sa f AT P f 2 2 2 2 2 4 2 2 4 2 2 ( ) ( ) + =− − + = m s s s f mf m Sa fT A Sa A T 16 2 16 2 4 2 4 2 功率谱密度如图所示

《通信原理》第五章数字基带传输系统习题 (2)由图5-7)中可以看出,该基带信号的功率密度中含有频率一元的离散分量,故 可以提取码元同步所需的须*人=乙的分量。 由题(1)中的结果,该基带信号的离散谱分量P,(@)为 s-m) 当m取士1时,即了=与时,有 =艺✉}-小立✉}U+》 所以该频率分量的功率为 -✉4 3.设某二进制数字基带信号中,数字信号“1”和“0”分别由g()和g()表示,且“1” 和“0”出现的概率相等,g(t)是余弦频谱脉冲,即 (1)写出该数字基带信号的功率谱密度表达式,并画出功率谱密度图: (2)从该数字基带信号中能否直接提取频率人,=元的分量。 (3》)若码元间隔=10~,试求该数字基带信号的传码率及颜宽度 解 (1)当数字信号“1”和“0”等概率出现时,双极性基带信号的功率谱密度 PU)=f,lGrX 已知g0= ,其傅立叶变换为G)=4 +rMs克 ,其他f 代入功率罐密度表达式中,有PU)-活0+c0s亚15乙,如国所示 第39页
《通信原理》第五章 数字基带传输系统 习题 第39页 (2)由图 5-7(b)中可以看出,该基带信号的功率谱密度中含有频率 s s T f 1 = 的离散分量,故 可以提取码元同步所需的频率 s s T f 1 = 的分量。 由题(1)中的结果,该基带信号的离散谱分量 () Pv 为 ( ) ( ) + =− − = m v mfs f m Sa A P f 16 2 4 2 当 m 取 1 时,即 s f = f 时,有 ( ) ( ) ( ) + =− + =− + − + = m s m v s Sa f f A Sa f f A P f 16 2 16 2 4 2 4 2 所以该频率分量的功率为 ( ) 4 2 4 2 4 2 2 16 2 16 2 A Sa A Sa A P f v = + = 3. 设某二进制数字基带信号中,数字信号“1”和“0”分别由 g(t)和-g(t)表示,且“1” 和“0”出现的概率相等,g(t)是余弦频谱脉冲,即 ( ) − = s s s T t Sa T t T t g t 2 2 4 1 cos 2 1 (1) 写出该数字基带信号的功率谱密度表达式,并画出功率谱密度图; (2) 从该数字基带信号中能否直接提取频率 s s T f 1 = 的分量; (3) 若码元间隔 T s s 3 10− = ,试求该数字基带信号的传码率及频谱宽度。 解: (1) 当数字信号“1”和“0”等概率出现时,双极性基带信号的功率谱密度 ( ) ( ) 2 P f f G f s s = 已知 ( ) − = s s s T t Sa T t T t g t 2 2 4 1 cos 2 1 ,其傅立叶变换为 ( ) ( ) + = f T fT f T G f s s s 0,其他 1 1 cos , 4 代入功率谱密度表达式中,有 ( ) ( ) s s s s T fT f T P f 1 1 cos , 16 = + ,如图所示:

《通信原理》第五章数字基希传输系统习题 4双装性玉字基布台号的基本冲夜形知用所示,它是一个高度为上宽度”一宁子,的能形 脉冲,且已知数字信号“1”的出现概率为14。 (1)该双极性信号的功率谱密度的表达式,并画出功率谱密度图: (2)由该双极性信号中能否直接提取频率为了=元的分量?若能,试计算该分量的功率, 解:(1)双极性基带信号的功率谱密度为 P(f)=4f.p(1-p)G()+>lf,(2p-1)G(mf.)5(f-mf,) 当P=14时,有 )cs-m) 80-4s3 已知 ”Q其福,故GU=:血时 将上试入B.得pU)-rw(+立omrU-) 4 第40页
《通信原理》第五章 数字基带传输系统 习题 第40页 4. 双极性数字基带信号的基本脉冲波形如图所示。它是一个高度为 1,宽度 Ts 3 1 = ,的矩形 脉冲,且已知数字信号“1”的出现概率为 1/4。 (1)该双极性信号的功率谱密度的表达式,并画出功率谱密度图; (2) 由该双极性信号中能否直接提取频率为 s s T f 1 = 的分量?若能,试计算该分量的功率。 解:(1)双极性基带信号的功率谱密度为 ( ) ( ) ( ) ( ) ( ) ( )s m Ps f = f s p − p G f + f s p − G mfs f − mf + =− 2 2 4 1 2 1 当 P=1/4 时,有 ( ) ( ) ( ) ( )s m s s s s G mf f mf f P f = f G f + − + =− 2 2 2 4 4 3 已知 = t t g t 0,其他 2 1, ( ) , 故 ( ) Sa f f f G f = = sin ( ) 将上式代入 P (f ) s , 得 ( ) ( ) ( ) ( )s m s s s s Sa mf f mf f P f = f Sa f + − + =− 2 2 2 2 2 4 4 3

《通信原理》第五章数字基带传输系统习题 将:=工代入上式中得 )-m) 功率谱密度如图所示。 2)由图可以看出,由该双极性信号可以直接提取频率为了,=了的分量 基带台号中的高散清分是为2o)-6三如得}U-财) 当m去正负1时有 o-s得U-+眉}U+d 所以频*为人=之分墨的功*为R®石心(得}6如) 5.已知信息代码为100000000011,求相应的AM码、HDB3码、PST码及双相码 解: AM码:+100000000-1+1 HDB3码:+1000+V-B00-V0+1-1 PST码:(+模式)+0-+.+.+.+ (-模式)0++++ 双相码:100101010101010101011010 6.己知信息代码为1010000011000011,试确定相应的AMI码及HDB3码,并画出波形图。 AM码:+10-100000+1-10000+1-1 BHD3码:+10-1000-V0+1-1+B00+V-1+1 第41页
《通信原理》第五章 数字基带传输系统 习题 第41页 将 Ts 3 1 = 代入上式中得 ( ) ( )s m s s s f mf m Sa f T P f T Sa − + = + =− 36 3 1 12 3 1 2 2 功率谱密度如图所示。 (2)由图可以看出,由该双极性信号可以直接提取频率为 s s T f 1 = 的分量。 该基带信号中的离散谱分量为 ( ) + =− − = m v mfs P Sa f 36 3 1 ( ) 2 当 m 去正负 1 时有 ( ) ( ) v s s P Sa f f Sa f + f − + = 36 3 1 36 3 1 ( ) 2 2 所以频率为 s s T f 1 = 分量的功率为 2 2 2 8 3 36 3 1 36 3 1 ( ) = + Pv = Sa Sa 5. 已知信息代码为 100000000011,求相应的 AMI 码、HDB3 码、PST 码及双相码。 解: AMI 码:+100000000-1+1 HDB3 码:+1000+V –B00-V0+1-1 PST 码:(+模式)+0-+-+-+-++- (-模式)-0-+-+-+-++- 双相码:10 01 01 01 01 01 01 01 01 01 10 10 6. 已知信息代码为 1010000011000011,试确定相应的 AMI 码及 HDB3 码,并画出波形图。 AMI 码:+10-100000+1-10000+1-1 BHD3 码:+1 0 –1 0 0 0 –V 0 +1 –1 + B 0 0 +V –1 +1

《通信原理》第五章数字基希传输系统习题 7.某基带传输系统接收滤波器输出信号的基本脉冲为如图所示的三角形。 (1)求该基带传输系统的传输函数H@) (2)设信道的传输函数C(@)=1,发送滤波器和接收滤波器具有相同的传输函数,即 C,(回)=C(@),试求此时的C,(o)或Cr(o)的表达式。 -psz (1)由图得 0,其他1 连基省系货的维备数为)-广0山-子如(受}片 (2)基带传输的传输函数由发送滤波器、信道和接受滤波器组成,即 H(@)=G.(OC(oC(0) 若Co)=lG,o)=Co),则Hlo)=G,oc.o)=Co旷c,(of uco-co)-阿-5} 8.设某基带传输系统具有如图所示的三角形传输函数: 第42页
《通信原理》第五章 数字基带传输系统 习题 第42页 7. 某基带传输系统接收滤波器输出信号的基本脉冲为如图所示的三角形。 (1) 求该基带传输系统的传输函数 H() (2) 设信道的传输函数 C() =1 ,发送滤波器和接收滤波器具有相同的传输函数,即 () () CT =CR ,试求此时的 () CT 或 () CR 的表达式。 解 (1) 由图得 ( ) − − = t t T T t h t T s s s 0,其他 ,0 2 2 1 该基带传输系统的传输函数为 ( ) ( ) s t j j t s s e T Sa T H h t e dt 2 2 2 4 + − − − = = (2) 基带传输的传输函数由发送滤波器、信道和接受滤波器组成,即 () () () () H = GT C CR 若 () () () C = GT =CR 1, ,则 ( ) ( ) ( ) ( ) ( ) 2 2 H = GT CR = CR GT 所以 ( ) ( ) ( ) s t j e T Sa T G C H s s T R 4 2 4 − = = = 8. 设某基带传输系统具有如图所示的三角形传输函数:

《通信原理》第五章数字基带传输系统习题 个H(W) 、1 一w。 0 Wo (1)求该系统接收滤波器输出基本脉冲的时间表达式: (2)当数字基带信号饿传码率R。=一时,用奈奎斯特准则验证该系统能否实现无码间干扰 传输? (1)由图可得 n)-(-aHjbso. 0,其他o 该系统输出基本脉冲的时间表达式为 0上ow-2() (2)根据奈奎斯特准则,当系统能实现无码间干扰传输时,H@)应满足 Heg(o)= Σo+-cs号 oa号 容易验证,当65号=时∑a+-Σ0+2a讯小-∑e+2a小:C所 当传码率R。=。/π时,系统不能实现无码间干扰传输。 9.设基带传输系统的发送滤波器、信道及接收滤波器组成总特性为H(o),若要求以2/T,Baud 的速率进行数据传输,试检验图所示的满足消除抽样点上的码间干扰的条件否? 当-、若清足无码同干找传输条件,根据条室新行准则,基带系统的总特性 第43页
《通信原理》第五章 数字基带传输系统 习题 第43页 (1) 求该系统接收滤波器输出基本脉冲的时间表达式; (2) 当数字基带信号饿传码率 0 RB = 时,用奈奎斯特准则验证该系统能否实现无码间干扰 传输? 解 (1) 由图可得 ( ) − = 0,其他 , 1 1 0 H 0 该系统输出基本脉冲的时间表达式为 ( ) ( ) = = + 2 − 2 2 1 0 2 0 t h t H e d Sa j t (2) 根据奈奎斯特准则,当系统能实现无码间干扰传输时, H() 应满足 ( ) = + = s i s s T T i C T H Heq 0, , 2 容易验证,当( ) 时, ( 2 ) ( 2 ) ,所以 2 0 i H R i H 0 i C T H T i i B s i s = + = + = + 当传码率RB =0 /时,系统不能实现无码间干扰传输。 9. 设基带传输系统的发送滤波器、信道及接收滤波器组成总特性为 H() ,若要求以 2/ Ts Baud 的速率进行数据传输,试检验图所示的满足消除抽样点上的码间干扰的条件否? 解 当 时,若满足无码间干扰传输条件,根据奈奎斯特准则,基带系统的总特性 = s B T R 2
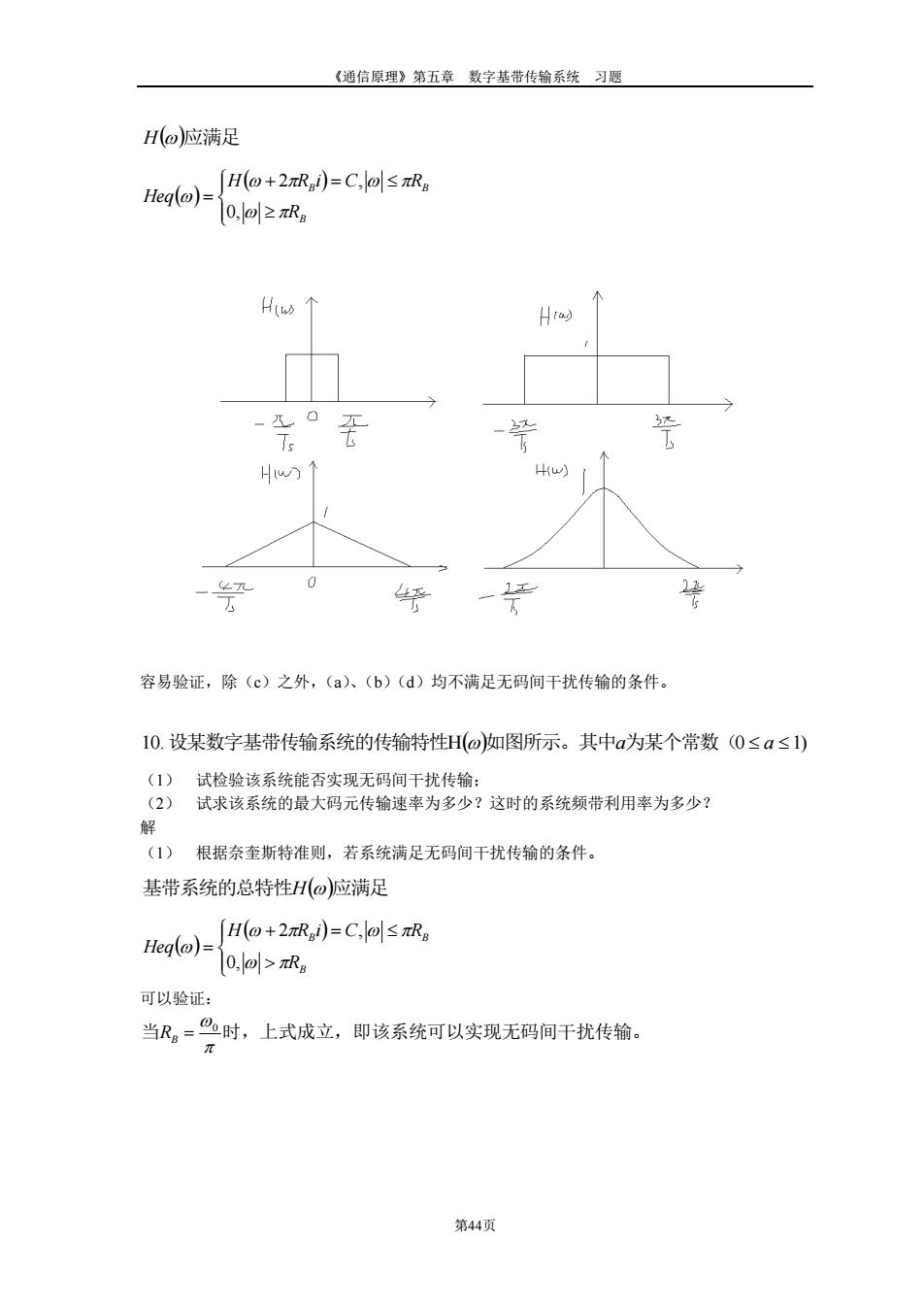
《通信原理》第五章数字基带传输系统习题 H(@)应满足 Heq(@)= Ho+2πR)=C,olsπR 0,o≥πR。 Hw个 -。 Hw 容易验证,除(c)之外,(a)、(b)(d)均不满足无码间干扰传输的条件。 10.设某数字基带传输系统的传输特性H(o)如图所示。其中a为某个常数(0≤a≤1) (1)试检验该系统能否实现无码间干扰传输: (2)试求该系统的最大码元传输速率为多少?这时的系统频带利用率为多少? (1)根据奈奎斯特准则,若系统满足无码间干扰传输的条件。 基带系统的总特性Ho)应满足 eglo)=o+2R)=C,asR 0.>Ra 可以验证: 当R。=鸟时,上式成立,即该系统可以实现无码间干扰传输。 第4页
《通信原理》第五章 数字基带传输系统 习题 第44页 H()应满足 ( ) ( ) + = = B B B R H R i C R Heq 0, 2 , 容易验证,除(c)之外,(a)、(b)(d)均不满足无码间干扰传输的条件。 10.设某数字基带传输系统的传输特性H()如图所示。其中a为某个常数(0 a 1) (1) 试检验该系统能否实现无码间干扰传输; (2) 试求该系统的最大码元传输速率为多少?这时的系统频带利用率为多少? 解 (1) 根据奈奎斯特准则,若系统满足无码间干扰传输的条件。 基带系统的总特性H()应满足 ( ) ( ) + = = B B B R H R i C R Heq 0, 2 , 可以验证: 当 时,上式成立,即该系统可以实现无码间干扰传输。 0 RB =
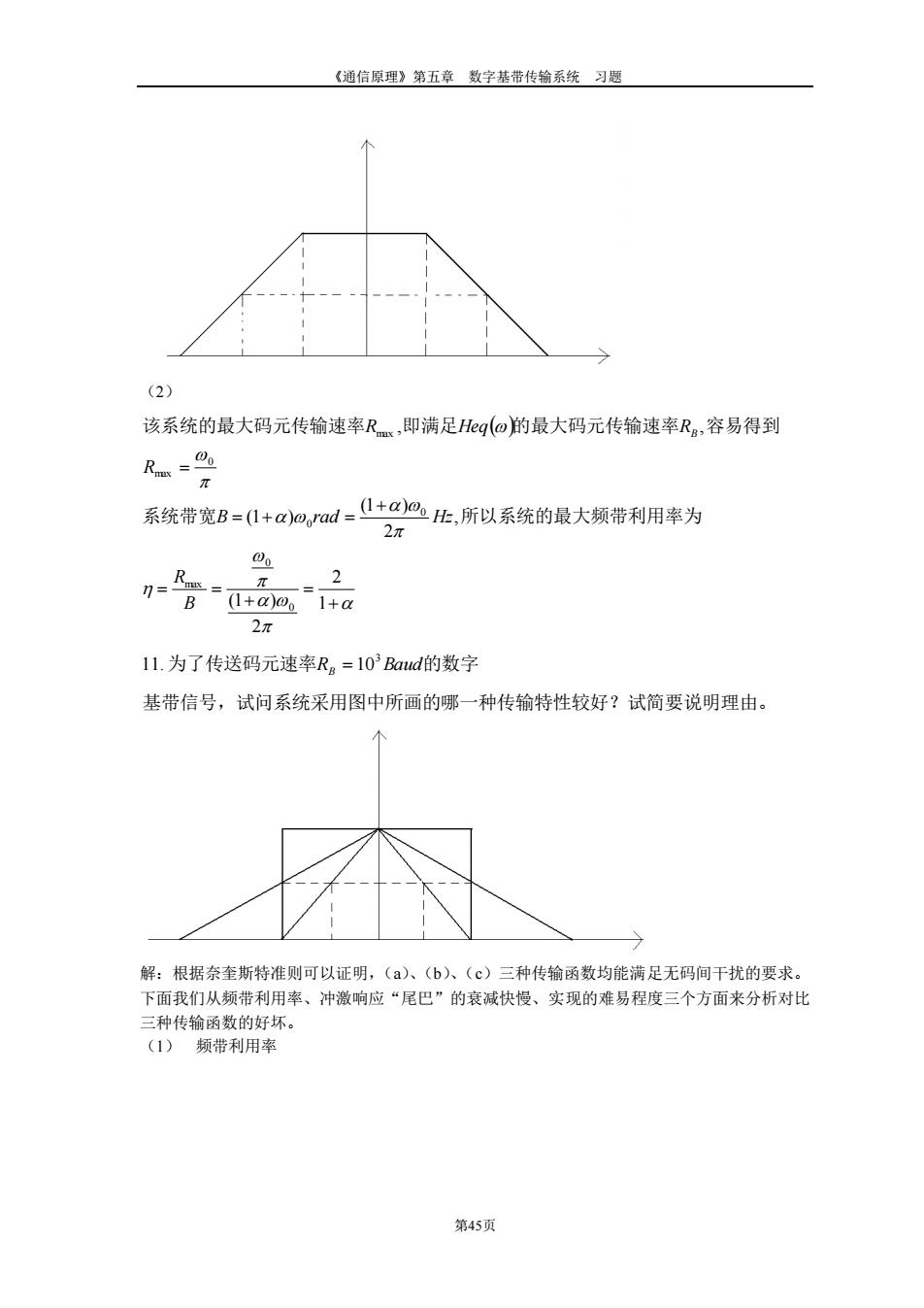
《通信原理》第五章数字基带传输系统习题 (2) 该系统的最大码元传输速率Rx,即满足Hg(o的最大码元传输速率Ra,容易得到 系统带宽B=1+a9ad=-L+a@:,所以系统的最大频带利用率为 2n t"lia 2 2元 11.为了传送码元速率R。=103Baud的数字 基带信号,试问系统采用图中所画的哪一种传输特性较好?试简要说明理由。 解:根据奈奎斯特准则可以证明,(a)、(b)、(c)三种传输函数均能满足无码间干扰的要求, 下面我们从频带利用率、冲激响应“尾巴”的衰减快慢、实现的难易程度三个方面来分析对比 三种传输函数的好坏。 (1)频带利用率 第45页
《通信原理》第五章 数字基带传输系统 习题 第45页 (2) ( ) + = + = = + = + = = 1 2 2 (1 ) , 2 (1 ) (1 ) , , 0 0 max 0 0 0 max max B R B rad Hz R R Heq RB 系统带宽 所以系统的最大频带利用率为 该系统的最大码元传输速率 即满足 的最大码元传输速率 容易得到 基带信号,试问系统采用图中所画的哪一种传输特性较好?试简要说明理由。 11. 为了传送码元速率RB = 103Baud的数字 解:根据奈奎斯特准则可以证明,(a)、(b)、(c)三种传输函数均能满足无码间干扰的要求。 下面我们从频带利用率、冲激响应“尾巴”的衰减快慢、实现的难易程度三个方面来分析对比 三种传输函数的好坏。 (1) 频带利用率

《通信原理》第五章数字基带传输系统习题 三种波形的传输速率均为R。=10O0Baud,传输函数(a)的带宽为 B。=2x103压 其频带利用率 传输函数(b)的带宽为 B。-103 其频带利用率 传输函数(b)的带宽为 B。=102k 其频带利用率 =1Baud /HE 显然 n。<%=ne (2)冲激响应“尾巴”的衰减快慢程度 (a以、(b)和(c)三种传输特性的时域波形分别为 h.)=2×103Sa22×103m) h,0-2x103Sa2x103m) h.0)=1035a2t03m) 其中(a)、(c)的尾巴以一的速度衰减,而(b) 的尾巴以'的速度衰减,故从时域波形的尾巴衰减速度 来看,传输特性(a)和(c)较好。 (3)从实现的难易程度来看,因为b为理想低通特性, 物理上不易实现,而a和c比较容易实现。 综上所述,传输特性c较好。 12.二进制基带系统的分析模型如图所示,现已知 H)=T(+cosos 0其他1 试确定该系统的最高的码元传输速率R及相应码元间隔T,。 第46页
《通信原理》第五章 数字基带传输系统 习题 第46页 Baud Hz B R B Hz b Baud Hz B R B Hz R Baud a b B a b a B a a B 1 / 1000 1000 10 0.5 / 2 10 1000 2 10 1000 , ( ) 3 3 3 = = = = = = = = = 其频带利用率 传输函数( )的带宽为 其频带利用率 三种波形的传输速率均为 传输函数 的带宽为 传输函数(b)的带宽为 a b c c B c c Baud Hz B R B Hz = = = = = 显然 其频带利用率 1 / 1000 1000 103 (2) 冲激响应“尾巴”的衰减快慢程度 (a)、(b)和(c)三种传输特性的时域波形分别为 ( ) ( ) ( ) ( ) h (t) Sa ( t) h t Sa t h t Sa t c b a 3 2 3 3 3 3 2 3 10 10 2 10 2 10 2 10 2 10 = = = 综上所述,传输特性 较好。 物理上不易实现,而 和 比较容易实现。 ( )从实现的难易程度来看,因为 为理想低通特性, 来看,传输特性( )和( )较好。 的尾巴以 的速度衰减,故从时域波形的尾巴衰减速度 其中( )、( )的尾巴以 的速度衰减,而( ) c a c b a c t b t a c 3 1 1 2 12. 二进制基带系统的分析模型如图所示,现已知 ( ) ( ) 试确定该系统的最高的码元传输速率 及相应码元间隔 。 其他 RB Ts t H + = 0, 1 cos , 0 0 0