
第二章随机变量及其分布 2.1随机变量的概念. 1 2.2 离散型随机变量. 5 2.2.1 0-1分布 8 2.2.2 二项分布 9 2.2.3 几何分布(Geometric distribution) 12 2.2.4 Pascal分布(负二项分布).. 16 2.2.5 Poisson分布 20 2.2.6 离散的均匀分布... 27 Previous Next First Last Back Forward 1
第二章随机变量及其分布 2.1 随机变量的概念 . . . . . . . . . . . . . . . . . 1 2.2 离散型随机变量 . . . . . . . . . . . . . . . . . 5 2.2.1 0-1 分布 . . . . . . . . . . . . . . . . . 8 2.2.2 二项分布 . . . . . . . . . . . . . . . . 9 2.2.3 几何分布 (Geometric distribution) . . 12 2.2.4 Pascal 分布 (负二项分布) . . . . . . . 16 2.2.5 Poisson 分布 . . . . . . . . . . . . . . 20 2.2.6 离散的均匀分布 . . . . . . . . . . . . . 27 Previous Next First Last Back Forward 1

2.1 随机变量的概念 随机变量是其值随机会而定的变量。 以X表示掷一次骰子得到的点数,X是一个随机变量.它可以 TExample 取{1,2,3,4,5,6}中的一个值,但到底取那个值,要等掷了骰子才知 道 Example 一张奖券的中奖金额是一个随机变量.它的值要等开奖以后才知 TExample 道 ⊥Example Previous Next First Last Back Forward
2.1 随机变量的概念 随机变量是其值随机会而定的变量。 ↑Example 以 X 表示掷一次骰子得到的点数, X 是一个随机变量. 它可以 取 {1, 2, 3, 4, 5, 6} 中的一个值,但到底取那个值,要等掷了骰子才知 道. ↓Example ↑Example 一张奖券的中奖金额是一个随机变量. 它的值要等开奖以后才知 道. ↓Example Previous Next First Last Back Forward 1

在一批产品中随机地抽出100个产品,其中所含的废品数是一个 TExample 随机变量.它的值要等检查了所有抽出的产品后才知道. ↓Example 在另外的例子中,随机试验的结果虽然不是一个数,但仍可用数 来描述, 掷一枚硬币出现正面或反面. TExample ↓Example 2, W=W1 X(u)= W=w2,W3 0 W=WA Example Previous Next First Last Back Forward 2
↑Example 在一批产品中随机地抽出 100 个产品, 其中所含的废品数是一个 随机变量. 它的值要等检查了所有抽出的产品后才知道. ↓Example 在另外的例子中, 随机试验的结果虽然不是一个数, 但仍可用数 来描述. ↑Example 掷一枚硬币出现正面或反面. ↓Example X(ω) = 2, ω = ω1 1, ω = ω2, ω3 0, ω = ω4 ↑Example Previous Next First Last Back Forward 2

产品被分为正品或废品 ↓Example 上面两例中的结果均可用一个取值0,1的随机变量来描述,其中 可以1代表正面或正品,以0代表反面或废品. 事实上,对任意一个事件A,定义 w∈A, IA() 反之, 则事件A由随机变量IA表示出来.IA称为事件A的示性函数. 随机变量是把随机试验的结果,也就是样本空间,与一组实数联 系起来.这样的处理简化了原来的概率结构.例如某机构调查民众对 一提案的态度是支持(1)还是反对(0).如果随机访向50人,按照 古典概型,所有可能的结果有20个.但是如果我们用X记1的个 数来表示赞成者的人数,则X为一个随机变量.它的取值范围只在 Previous Next First Last Back Forward 3
产品被分为正品或废品. ↓Example 上面两例中的结果均可用一个取值 0,1 的随机变量来描述, 其中 可以 1 代表正面或正品, 以 0 代表反面或废品. 事实上, 对任意一个事件 A, 定义 IA(ω) = { 1 ω ∈ A , 0 反之 , 则事件 A 由随机变量 IA 表示出来. IA 称为事件 A 的示性函数. 随机变量是把随机试验的结果,也就是样本空间,与一组实数联 系起来. 这样的处理简化了原来的概率结构. 例如某机构调查民众对 一提案的态度是支持 (1) 还是反对 (0). 如果随机访问 50 人,按照 古典概型,所有可能的结果有 2 50 个. 但是如果我们用 X 记 1 的个 数来表示赞成者的人数,则 X 为一个随机变量. 它的取值范围只在 Previous Next First Last Back Forward 3

{0,1,·,50}.所以随机变量的引进有利于我们对所研究的问题进行 准确,简练的描述.又由于随机变量取实值,随机变量之间的运算就变 得容易了. 令2为一个样本空间.令X是定义在2上的一个实函数, 如果对2中的任意点w,总存在一个实数X(w)与之对应, Definition 则称X为一个(一维)随机变量. 常见的随机变量可以分为两大类.只取有限个或可数个值的随机 变量称为离散型随机变量;取连续的值且密度存在的随机变量称为连 续型随机变量.当然,存在既非离散型也非连续型的随机变量.但它们 在实际中并不常见,也不是我们这里研究的对象 Previous Next First Last Back Forward 4
{0, 1, · · · , 50}. 所以随机变量的引进有利于我们对所研究的问题进行 准确, 简练的描述. 又由于随机变量取实值, 随机变量之间的运算就变 得容易了. 令 Ω 为一个样本空间. 令 X 是定义在 Ω 上的一个实函数, 如果对 Ω 中的任意点 ω,总存在一个实数 X(ω) 与之对应, 则称 X 为一个 (一维) 随机变量. Definition 常见的随机变量可以分为两大类. 只取有限个或可数个值的随机 变量称为离散型随机变量;取连续的值且密度存在的随机变量称为连 续型随机变量. 当然, 存在既非离散型也非连续型的随机变量. 但它们 在实际中并不常见, 也不是我们这里研究的对象. Previous Next First Last Back Forward 4

2.2 离散型随机变量 设X为一随机变量.如果X只取有限个或可数个值,则称 Definition X为一个(一维)离散型随机变量. 由于一个随机变量的值是由试验结果决定的,因而是以一定的概 率取值.这个概率分布称为离散型随机变量的概率函数」 设X为一离散型随机变量,其全部可能值为{a1,a2,}.则 p=P(X=a),i=1,2, (2.1) Definition 称为X的概率质量函数(probability mass function, pm)或分布律. Previous Next First Last Back Forward 5
2.2 离散型随机变量 设 X 为一随机变量. 如果 X 只取有限个或可数个值,则称 X 为一个 (一维) 离散型随机变量. Definition 由于一个随机变量的值是由试验结果决定的,因而是以一定的概 率取值. 这个概率分布称为离散型随机变量的概率函数. 设 X 为一离散型随机变量,其全部可能值为 {a1, a2, ...}. 则 pi = P(X = ai), i = 1, 2, ... (2.1) 称为 X 的概率质量函数 (probability mass function, pmf) 或分布律. Definition Previous Next First Last Back Forward 5

概率质量函数{P:,i=1,2,}必须满足下列条件: :≥0,i=1,2,… ∑n=1. F)=P(X≤)=∑P(X=a)=∑p i:p≤r P(X=ai)=P(ai-1<X<ai)=F(ai)-F(ai-1) 概率质量函数(2.1)指出了全部概率1是如何在X的所有可能值之 间分配的.它可以列表的形式给出: 可能值 al 12 (2.2) 概率 Pi Pi 有时也把(22)称为随机变量X的分布表. Previous Next First Last Back Forward 6
概率质量函数 {pi, i = 1, 2, ..} 必须满足下列条件: pi ≥ 0, i = 1, 2, .... ∑ i pi = 1. F(x) = P(X ≤ x) = ∑ i:pi≤x P(X = ai) = ∑ i:pi≤x pi P(X = ai) = P(ai−1 < X ≤ ai) = F(ai) − F(ai−1) 概率质量函数 (2.1) 指出了全部概率 1 是如何在 X 的所有可能值之 间分配的. 它可以列表的形式给出: 可能值 a1 a2 ... ai ... 概率 p1 p2 ... pi ... (2.2) 有时也把 (2.2) 称为随机变量 X 的分布表. Previous Next First Last Back Forward 6

设2为一样本空间.X为定义于其上的一个离散型随机变量, 其取值为x1,x2,…令A为{红1,x2,…}的任意一个子集.事件{X 取值于A中}的概率可根据概率的可加性来计算: P(4)=∑P(X= 这样知道了离散型随机变量X的概率函数,我们就能给出关于X的 任何概率问题的回答 下面我们给出常见的离散型分布.在描述离散概率模型时, Bernoulli试验是最早被研究且应用及其广泛的概率模型 设一个随机试验只有两个可能结果A和A,则称此试验为一 Definition Bernoulli试验. Previous Next First Last Back Forward
设 Ω 为一样本空间. X 为定义于其上的一个离散型随机变量, 其取值为 x1, x2, ..... 令 A 为 {x1, x2, ...} 的任意一个子集. 事件 {X 取值于 A 中} 的概率可根据概率的可加性来计算: P(A) = ∑ x∈A P(X = x). 这样知道了离散型随机变量 X 的概率函数,我们就能给出关于 X 的 任何概率问题的回答. 下面我们给出常见的离散型分布. 在描述离散概率模型时, Bernoulli 试验是最早被研究且应用及其广泛的概率模型. 设一个随机试验只有两个可能结果 A 和 A¯, 则称此试验为一 Bernoulli 试验. Definition Previous Next First Last Back Forward 7

设将一个可能结果为A和A的Bernoulli试验独立地重 复n次,使得事件A每次出现的概率相同,则称此试验为 Definition n重Bernoulli试验. 下面的0-1分布和二项分布都是以Bernoulli试验为基础的, 2.2.10-1分布 设随机变量X只取0,1两值,P(X=1)=p,P(X=0)= 1-p,则称X服从0-1分布或Bernoulli分布.0-1分布是很多古典 概率模型的基础。 Previous Next First Last Back Forward 8
设将一个可能结果为 A 和 A¯ 的 Bernoulli 试验独立地重 复 n 次, 使得事件 A 每次出现的概率相同, 则称此试验为 n 重 Bernoulli 试验. Definition 下面的 0-1 分布和二项分布都是以 Bernoulli 试验为基础的. 2.2.1 0-1 分布 设随机变量 X 只取 0,1 两值,P(X = 1) = p,P(X = 0) = 1 − p,则称 X 服从 0-1 分布或 Bernoulli 分布. 0-1 分布是很多古典 概率模型的基础. Previous Next First Last Back Forward 8
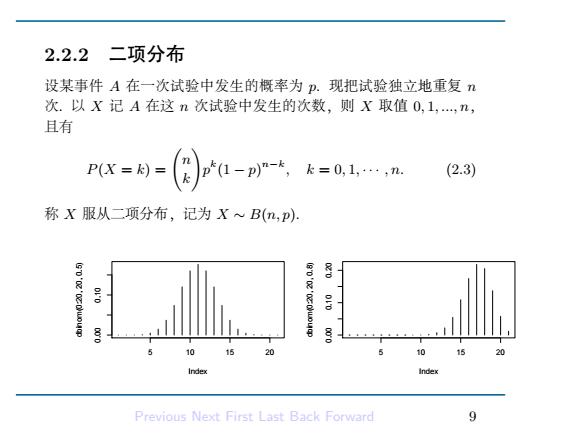
2.2.2 二项分布 设某事件A在一次试验中发生的概率为p.现把试验独立地重复n 次.以X记A在这n次试验中发生的次数,则X取值0,1,,n, 且有 P(X=k) (1-p)m-,k=0,1,…,n. (2.3) 称X服从二项分布,记为X~B(n,p): 20 Index index Previous Next First Last Back Forward
2.2.2 二项分布 设某事件 A 在一次试验中发生的概率为 p. 现把试验独立地重复 n 次. 以 X 记 A 在这 n 次试验中发生的次数,则 X 取值 0, 1, ..., n, 且有 P(X = k) = ( n k ) p k (1 − p) n−k , k = 0, 1, · · · , n. (2.3) 称 X 服从二项分布,记为 X ∼ B(n, p). 5 10 15 20 0.00 0.10 Index dbinom(0:20, 20, 0.5) 5 10 15 20 0.00 0.10 0.20 Index dbinom(0:20, 20, 0.8) Previous Next First Last Back Forward 9