
第七讲:假设检验 72一样本和两样本总体参数检验 1 7.2.1一样本正态总体参数检验 1 7.2.2两样本正态总体的情形.. 13 7.2.3 成对数据···· 18 7.2.40-1分布中未知参数p的假设检验 19 7.2.5置信区间和假设检验之间的关系..·· 21 Previous Next First Last Back Forward
第七讲: 假设检验 7.2 一样本和两样本总体参数检验 . . . . . . . . . 1 7.2.1 一样本正态总体参数检验 . . . . . . . 1 7.2.2 两样本正态总体的情形 . . . . . . . . . 13 7.2.3 成对数据 . . . . . . . . . . . . . . . . 18 7.2.4 0-1 分布中未知参数 p 的假设检验 . . 19 7.2.5 置信区间和假设检验之间的关系 . . . . 21 Previous Next First Last Back Forward 1

7.2一样本和两样本总体参数检验 本节介绍最基本的假设检验问题:一样本和两样本正态总体的有 关均值和方差的检验,简单的大样本检验(0-1分布参数的假设检验). 7.2.1一样本正态总体参数检验 一股地,设总体X~N(4,a2),-00:X1,·,Xn 是取自总体X的一个样本.取显著性水平为α.则可能考虑的参数有 均值4和方差σ2: (1)方差已知时均值的检验 先考虑双侧假设,即要检验 H0:4=40+H1:μ≠0. Previous Next First Last Back Forward 1
7.2 一样本和两样本总体参数检验 本节介绍最基本的假设检验问题: 一样本和两样本正态总体的有 关均值和方差的检验, 简单的大样本检验 (0-1 分布参数的假设检验). 7.2.1 一样本正态总体参数检验 一般地, 设总体 X ∼ N(µ, σ2 ), −∞ 0; X1, · · · , Xn 是取自总体 X 的一个样本. 取显著性水平为 α. 则可能考虑的参数有 均值 µ 和方差 σ 2 : (1) 方差已知时均值的检验 先考虑双侧假设, 即要检验 H0 : µ = µ0 ↔ H1 : µ ̸= µ0. Previous Next First Last Back Forward 1

由于:的极大似然估计为灭,取“标准化”后的检验统计量 Z=Z(X1,…,Xn)=√元2 注意到当Ho成立时,U~N(0,1),|Z应该较小,反之当U的观 测值(c1,·,xn)较大时,不利于零假设Ho应该拒绝之.所以选拒 绝域形如 IZ>}. 要求显著性水平为α,即 PHo(IZ\>T)=a, 解得r=2。/2·于是检验的拒绝域为 {|Z\>ua2}. 即当观测值(x1,·,xn)满足不等式 V-ol >ua/2 Q Previous Next First Last Back Forward 2
由于 µ 的极大似然估计为 X¯, 取 “标准化” 后的检验统计量 Z = Z(X1, · · · , Xn) = √ n X¯ − µ0 σ 注意到当 H0 成立时, U ∼ N(0, 1), |Z| 应该较小, 反之当 |U| 的观 测值 z(x1, · · · , xn) 较大时, 不利于零假设 H0 应该拒绝之. 所以选拒 绝域形如 {|Z| > τ}. 要求显著性水平为 α, 即 PH0 (|Z| > τ ) = α, 解得 τ = zα/2. 于是检验的拒绝域为 {|Z| > uα/2}. 即当观测值 (x1, · · · , xn) 满足不等式 √ n |x¯ − µ0| σ > uα/2 Previous Next First Last Back Forward 2

时拒绝Ho 类似地,检验右侧假设 Ho:μ=o分H1:4>μ0或者H0:μ≤40+H:μ>0 仍然用统计量Z,由于Z大时不利于Ho,取拒绝域为 {Z>ua}. 而检验另一个左侧假设 H0:4=40台H1:4<μ0或者H0:4≤0+1:4<0 的拒绝域为 {Z<-ua}. 虽然我们取的临界值只考虑使检验在μ=0处的犯I类错误的概率 为α,从检验的拒绝域的形状上可直接看出来在零假设下μ≤o(或 4之o)时犯第I类错误的概率恒小于或等于a. Previous Next First Last Back Forward 3
时拒绝 H0. 类似地, 检验右侧假设 H0 : µ = µ0 ↔ H1 : µ > µ0 或者 H0 : µ ≤ µ0 ↔ H1 : µ > µ0 仍然用统计量 Z, 由于 Z 大时不利于 H0, 取拒绝域为 {Z > uα} . 而检验另一个左侧假设 H0 : µ = µ0 ↔ H1 : µ < µ0 或者 H0 : µ ≤ µ0 ↔ H1 : µ < µ0 的拒绝域为 {Z < −uα} . 虽然我们取的临界值只考虑使检验在 µ = µ0 处的犯 I 类错误的概率 为 α, 从检验的拒绝域的形状上可直接看出来在零假设下 µ ≤ µ0 (或 µ ≥ µ0) 时犯第 I 类错误的概率恒小于或等于 α. Previous Next First Last Back Forward 3
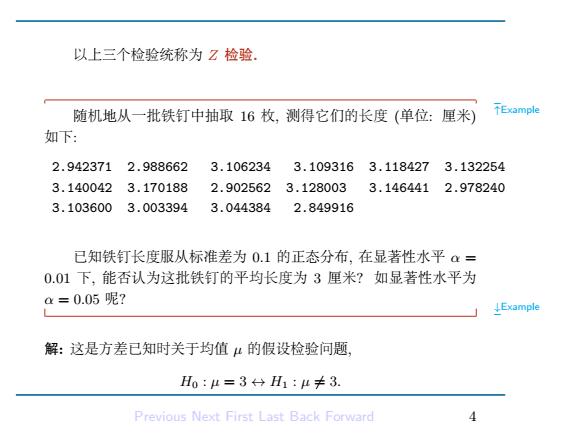
以上三个检验统称为Z检验: 随机地从一批铁钉中抽取16枚,测得它们的长度(单位:厘米) ↑Example 如下: 2.9423712.988662 3.106234 3.1093163.118427 3.132254 3.1400423.170188 2.9025623.128003 3.1464412.978240 3.1036003.003394 3.044384 2.849916 已知铁钉长度服从标准差为0.1的正态分布,在显著性水平a= 0.01下,能否认为这批铁钉的平均长度为3厘米?如显著性水平为 a=0.05呢? Example 解:这是方差已知时关于均值μ的假设检验问题, Ho:μ=3←+H1:4≠3. Previous Next First Last Back Forward 4
以上三个检验统称为 Z 检验. ↑Example 随机地从一批铁钉中抽取 16 枚, 测得它们的长度 (单位: 厘米) 如下: 2.942371 2.988662 3.106234 3.109316 3.118427 3.132254 3.140042 3.170188 2.902562 3.128003 3.146441 2.978240 3.103600 3.003394 3.044384 2.849916 已知铁钉长度服从标准差为 0.1 的正态分布, 在显著性水平 α = 0.01 下, 能否认为这批铁钉的平均长度为 3 厘米? 如显著性水平为 α = 0.05 呢? ↓Example 解: 这是方差已知时关于均值 µ 的假设检验问题, H0 : µ = 3 ↔ H1 : µ ̸= 3. Previous Next First Last Back Forward 4

取检验统计量为Z=√元(下-3)/0.1,检验的拒绝域为|Z)>u。/2: 由样本算得检验统计量的值为z≈2.16,如显著性水平为0.01,则临 界值为u0.005≈2.58,跟检验统计量的值比较发现不能拒绝零假设, 即不能推翻铁钉平均长度为3厘米的假设:而如果显著性水平为0.05 时,临界值为0.25=1.96,此时可以拒绝零假设,认为铁钉平均长度 不等于3厘米.这个例子说明结论可能跟显著性水平的选择有关:显 著性水平越小,零假设被保护得越好从而更不容易被拒绝 对正态总体N(4,σ2)(其中σ2已知)下的假设检验问题Ho:μ≥ Example 40+H1:μ0”该怎么办? ↓Example 解:根据功效函数和两类错误的定义,知道等价的要求 B(4)21-B,4<40 (7.1) 但是,当μ<0但μ接近o时,B。(4)≈a,而因为a,B一般都 很小,因此一般有α<1-B,这就看出要求(7.1)无法达到。我们只 Previous Next First Last Back Forward
取检验统计量为 Z = √ n(X¯ − 3)/0.1, 检验的拒绝域为 |Z| > uα/2. 由样本算得检验统计量的值为 z ≈ 2.16, 如显著性水平为 0.01, 则临 界值为 u0.005 ≈ 2.58, 跟检验统计量的值比较发现不能拒绝零假设, 即不能推翻铁钉平均长度为 3 厘米的假设; 而如果显著性水平为 0.05 时, 临界值为 u0.025 = 1.96, 此时可以拒绝零假设, 认为铁钉平均长度 不等于 3 厘米. 这个例子说明结论可能跟显著性水平的选择有关: 显 著性水平越小, 零假设被保护得越好从而更不容易被拒绝. ↑Example 对正态总体 N(µ, σ2 )(其中 σ 2 已知) 下的假设检验问题 H0 : µ ≥ µ0 ↔ H1 : µ 0”该怎么办? ↓Example 解:根据功效函数和两类错误的定义,知道等价的要求 βϕ(µ) ≥ 1 − β, µ < µ0 (7.1) 但是,当 µ < µ0 但 µ 接近 µ0 时,βϕ(µ) ≈ α,而因为 α, β 一般都 很小,因此一般有 α < 1 − β,这就看出要求 (7.1) 无法达到。我们只 Previous Next First Last Back Forward 5

能放松一些,要求对某个指定的山1<0,有 B.(4)≥1-B,μ<1 (7.2) 因为B()为μ的诚函数,因此等价于要求 B.(41)≥1-B 此即 (g四-)21- 等价的得到 n≥a2(ua+ug)2/八0-1)2 也即要满足题目中的要求,样本大小至少要达到上式右边那么大。口 Previous Next First Last Back Forward 6
能放松一些,要求对某个指定的 µ1 < µ0,有 βϕ(µ) ≥ 1 − β, µ < µ1 (7.2) 因为 βϕ(µ) 为 µ 的减函数,因此等价于要求 βϕ(µ1) ≥ 1 − β 此即 Φ (√ n(µ0 − µ1) σ − uα ) ≥ 1 − β 等价的得到 n ≥ σ 2 (uα + uβ) 2 /(µ0 − µ1) 2 也即要满足题目中的要求,样本大小至少要达到上式右边那么大。 Previous Next First Last Back Forward 6�

(2)方差未知时均值的检验 考虑检验 H0:4=H0+μ≠0 由于方差未知,可以在将元标准化的过程中用样本方差S2代替总体 方差σ2,得检验统计量 T=Vn2 由于在Ho下,T~tn-1,于是拒绝域取成 {0T>tm-1(a/2)}. 此检验称为检验. 类似地可以得到另外两个单侧假设的检验拒绝域,见表7.2.1中. Previous Next First Last Back Forward
(2) 方差未知时均值的检验 考虑检验 H0 : µ = µ0 ↔ µ ̸= µ0, 由于方差未知, 可以在将 X¯ 标准化的过程中用样本方差 S 2 代替总体 方差 σ 2 , 得检验统计量 T = √ n X¯ − µ0 S . 由于在 H0 下, T ∼ tn−1, 于是拒绝域取成 {|T| > tn−1(α/2)} . 此检验称为t 检验. 类似地可以得到另外两个单侧假设的检验拒绝域, 见表 7.2.1 中. Previous Next First Last Back Forward 7

(例7.2.1续)设方差未知,则在水平0.01和0.05下能否认为铁钉 TExample 平均长度为3厘米? Example 解:这是方差未知时关于均值4的假设检验问题, Ho:4=3←+H1:4≠3 取检验统计量为T=vm(灭-3)/S,检验的拒绝域为T>tn-1(a/2). 由样本算得检验统计量的值约为2.21,与显著性水平0.01对应临界 值t15(0.005)≈2.95比较,不能拒绝零假设,而与显著性水平0.05对 应临界值t15(0.025)≈2.13比较,可以拒绝零假设,即在显著性水平 0.01下不能拒绝铁钉平均长度为3厘米的假定,但在显著性水平0.05 下可以认为铁钉平均长度不等于3厘米此结论与方差已知情形一致 Previous Next First Last Back Forward 8
↑Example (例7.2.1续) 设方差未知, 则在水平 0.01 和 0.05 下能否认为铁钉 平均长度为 3 厘米? ↓Example 解: 这是方差未知时关于均值 µ 的假设检验问题, H0 : µ = 3 ↔ H1 : µ ̸= 3 取检验统计量为 T = √ n(X¯ − 3)/S, 检验的拒绝域为 |T| > tn−1(α/2). 由样本算得检验统计量的值约为 2.21, 与显著性水平 0.01 对应临界 值 t15(0.005) ≈ 2.95 比较, 不能拒绝零假设, 而与显著性水平 0.05 对 应临界值 t15(0.025) ≈ 2.13 比较, 可以拒绝零假设, 即在显著性水平 0.01 下不能拒绝铁钉平均长度为 3 厘米的假定, 但在显著性水平 0.05 下可以认为铁钉平均长度不等于 3 厘米, 此结论与方差已知情形一致. Previous Next First Last Back Forward 8

(3)方差的检验 考虑假设检验问题 H0:02=64H1:o2≠. 对均值已知的情形,由σ2的极大似然估计 62 可以构造检验统计量 1 x2=3 ∑(-四2=n 在。下,X~X后,X的平均值为n,而在下,X=三亭的 均值为需n≠n,因此当X的值过于偏离n时应该拒绝,于是拒 绝域取成 {x2x品(a/2)}. Previous Next First Last Back Forward 9
(3) 方差的检验 考虑假设检验问题 H0 : σ 2 = σ 2 0 ↔ H1 : σ 2 ̸= σ 2 0. 对均值已知的情形, 由 σ 2 的极大似然估计 σˆ 2 = 1 n ∑n i=1 (Xi − µ) 2 可以构造检验统计量 χ 2 = 1 σ 2 0 ∑n i=1 (Xi − µ) 2 = nσˆ 2 σ 2 0 . 在 H0 下, χ 2 ∼ χ 2 n, χ 2 的平均值为 n, 而在 H1 下, χ 2 = σ 2 σ2 0 nσˆ 2 σ2 的 均值为 σ 2 σ2 0 n ̸= n, 因此当 χ 2 的值过于偏离 n 时应该拒绝 H0, 于是拒 绝域取成 { χ 2 χ2 n(α/2)} . Previous Next First Last Back Forward 9