
第二章随机变量及其分布 2.3 多维分布与边际分布 1 2.3.1多维分布 1 2.3.2边缘分布 14 Previous Next First Last Back Forward 1
第二章随机变量及其分布 2.3 多维分布与边际分布 . . . . . . . . . . . . . . 1 2.3.1 多维分布 . . . . . . . . . . . . . . . . 1 2.3.2 边缘分布 . . . . . . . . . . . . . . . . 14 Previous Next First Last Back Forward 1

2.3多维分布与边际分布 2.3.1多维分布 在实际应用中,经常需要对所考虑的问题用多个变量来描述.我 们把多个随机变量放在一起组成向量,称为多维随机变量或者随机向 量 从一副扑克牌中抽牌时,可以用纸牌的花色和数字来说明其特征, 下Example Example 考虑一个打靶的试验.在靶面上取定一个直角坐标系.则命中的 TExample 位置可由其坐标(X,Y)来刻划.X,Y都是随机变量 ⊥Example Previous Next First Last Back Forward
2.3 多维分布与边际分布 2.3.1 多维分布 在实际应用中,经常需要对所考虑的问题用多个变量来描述. 我 们把多个随机变量放在一起组成向量,称为多维随机变量或者随机向 量. ↑Example 从一副扑克牌中抽牌时, 可以用纸牌的花色和数字来说明其特征. ↓Example ↑Example 考虑一个打靶的试验. 在靶面上取定一个直角坐标系. 则命中的 位置可由其坐标 (X, Y ) 来刻划. X,Y 都是随机变量. ↓Example Previous Next First Last Back Forward 1

设X=(X1,,Xn).如果每个X:都是一个随机变量, Definition i=1,·,n,则称X为n维随机变量或者随机向量 我们可以按照对常用一维随机变量的分类把常用的随机向量分 为离散型、连续型以及其他类型」 Previous Next First Last Back Forward 2
设 X = (X1, . . . , Xn). 如果每个 Xi 都是一个随机变量, i = 1, · · · , n,则称 X 为 n 维随机变量或者随机向量. Definition 我们可以按照对常用一维随机变量的分类把常用的随机向量分 为离散型、连续型以及其他类型. Previous Next First Last Back Forward 2

如果每一个X:都是一个离散型随机变量,i=1,,n,则称 X=(X1,,Xn)为一n维离散随机变量.设X:的所有 可能取值(有限或可数个)为{a1,a2,…},i=1,,n, 则称 Definition p(01,…,jn)=P(X1=a11,Xn=Anin)j1,,jm=1,2,… (2.1) 为n维随机交量X的概率函数. 容易证明概率函数具有下列性质: (1)p(0j1,,jn)≥0,ji=1,2,·,i=1,2,,n (2)∑pi1,,jn)=1. J1Jn Previous Next First Last Back Forward 3
如果每一个 Xi 都是一个离散型随机变量,i = 1, ..., n,则称 X = (X1, . . . , Xn) 为一 n 维离散随机变量. 设 Xi 的所有 可能取值 (有限或可数个) 为 {ai1, ai2, · · · }, i = 1, . . . , n, 则称 p(j1, · · · , jn) = P(X1 = a1j1 , . . . , Xn = anjn ), j1, ..., jn = 1, 2, ... (2.1) 为 n 维随机变量 X 的概率函数. Definition 容易证明概率函数具有下列性质: (1) p(j1, . . . , jn) ≥ 0, ji = 1, 2, · · · , i = 1, 2, . . . , n; (2) ∑ j1,··· ,jn p(j1, . . . , jn) = 1. Previous Next First Last Back Forward 3

设A1,·,An为某一实验下的完备事件群,即A1,…,An两 TExample 两互斥且和为2。记p%=P(Ak)k=1,.,n),则pk≥0,p1+ ·+p=1。现将实验独立的重复作N次,分别用X:表示事 件A:出现的次数(位=1,·,n)。则X=(X1,,Xn)为一离散 型随机向量,试求X的概率函数。此分布律称为多项分布,记为 M(N;p1,·,pm Example Previous Next First Last Back Forward 4
↑Example 设 A1, · · · , An 为某一实验下的完备事件群,即 A1, · · · , An 两 两互斥且和为 Ω。记 pk = P(Ak)(k = 1, . . . , n),则 pk ≥ 0, p1 + · · · + pn = 1。现将实验独立的重复作 N 次,分别用 Xi 表示事 件 Ai 出现的次数 (i = 1, · · · , n)。则 X = (X1, . . . , Xn) 为一离散 型随机向量,试求 X 的概率函数。此分布律称为多项分布, 记为 M(N; p1, . . . , pn). ↓Example 解: 由于试验独立进行, 总的结果数为 N,记结果 Ai 出现的次数为 ki,则 k1 + · · · + kn = N。因此相当于多组组合,所以 P(X1 = k1, · · · , Xn = kn) = N! k1! · · · kn! P(A1 · · · A1 . . . An · · · An) = N! k1! · · · kn! p k1 1 · · · p kn n , 其中 k1, . . . , kn 为非负整数且 k1 + · · · + kn = N. Previous Next First Last Back Forward 4

我们来看一下X:的分布:此时我们把试验结果分为两类,A:和 A:,则显然就是一个N重贝努里试验,因此 P(X:=)= (1-)N-k,k=1,N. 类似我们也可以找出(X,X)(i≠)的联合分布律,即为M(N,p,,1- p-p5) Previous Next First Last Back Forward 5
我们来看一下 Xi 的分布:此时我们把试验结果分为两类, Ai 和 A¯i,则显然就是一个 N 重贝努里试验,因此 P(Xi = ki) = ( N ki ) p ki i (1 − pi) N−ki , ki = 1, · · · , N. 类似我们也可以找出 (Xi, Xj )(i ̸= j) 的联合分布律,即为 M(N, pi, pj , 1− pi − pj ). Previous Next First Last Back Forward 5
我们具体来看一下二维离散分布.设二维离散型随机变量(X,Y) 的所有可能取值为{(x,):i=1,,n,j=1,2,,m}.这里mm 为有限数或者无穷.我们经常以列联表的形式来表示二维离散型随机 变量的概率分布.记 p=P(X=c,Y=),i=1,,n,j=1,,m. 则(X,Y)的概率函数可以用下表表示: 1 T2 Ym 行和 T1 p11 P12 4… Pim P1. 工2 p12 p22 p2m p2. .. 工n Pnl Pn2 Pnm Pn. 列和 p.1 p.2 p.m 1 Previous Next First Last Back Forward 6
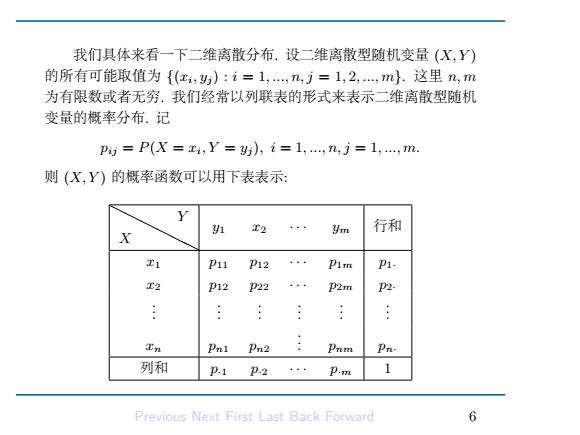
我们具体来看一下二维离散分布. 设二维离散型随机变量 (X, Y ) 的所有可能取值为 {(xi, yj ) : i = 1, ..., n, j = 1, 2, ..., m}. 这里 n, m 为有限数或者无穷. 我们经常以列联表的形式来表示二维离散型随机 变量的概率分布. 记 pij = P(X = xi, Y = yj ), i = 1, ..., n, j = 1, ..., m. 则 (X, Y ) 的概率函数可以用下表表示: ❍ X ❍❍❍❍❍ Y y1 x2 · · · ym 行和 x1 p11 p12 · · · p1m p1· x2 p12 p22 · · · p2m p2· . . . . . . . . . . . . . . . . . . xn pn1 pn2 . . . pnm pn· 列和 p·1 p·2 · · · p·m 1 Previous Next First Last Back Forward 6

从一个包含五个黑球,六个白球和七个红球的罐子里抽取四个 TExample 球.令X是抽到白球的数目,Y是抽到红球的数目.则二维随机变量 (X,Y)的概率函数为 p(,)= 90(4- ,0≤x+y≤4. (2.2) Example 以列联表表示,即为 Previous Next First Last Back Forward
↑Example 从一个包含五个黑球, 六个白球和七个红球的罐子里抽取四个 球. 令 X 是抽到白球的数目, Y 是抽到红球的数目. 则二维随机变量 (X, Y ) 的概率函数为 p(x, y) = ( 6 x )(7 y )( 5 4−x−y ) ( 18 4 ) , 0 ≤ x + y ≤ 4. (2.2) ↓Example 以列联表表示, 即为 Previous Next First Last Back Forward 7

X 0 2 3 4 行和 0 立 102 53 品 1 2 磊 3 35 7 77 612 0 4 7 612 1 列和 99 1 1 612 34 类似于一维连续型随机变量, 连续型随机向量的也是由密度函数 来刻画的. Previous Next First Last Back Forward 8
❍ Y ❍❍❍❍❍ X 0 1 2 3 4 行和 0 1 612 1 51 5 102 5 153 1 204 11 102 1 7 306 7 51 35 204 7 153 77 204 2 7 102 7 34 7 68 7 17 3 35 612 7 102 77 612 4 7 612 7 612 列和 99 612 22 51 11 34 4 51 1 204 1 类似于一维连续型随机变量, 连续型随机向量的也是由密度函数 来刻画的. Previous Next First Last Back Forward 8

称X=(X1,,Xn)为n维连续型随机变量,如果存在 R”上的非负函数f(x1,,xn),使得对任意的-oo< a1≤b1<+∞,,-0∞<an≤bn<+o,有 Definition Pa≤x≤a.≤X.s)=-feah,an 则称∫为X的概率密度函数。 Previous Next First Last Back Forward 9
称 X = (X1, . . . , Xn) 为 n 维连续型随机变量,如果存在 R n 上的非负函数 f(x1, . . ., xn),使得对任意的 −∞ < a1 ≤ b1 < +∞, ..., −∞ < an ≤ bn < +∞, 有 P(a1 ≤ X1 ≤ b1, ..., an ≤ Xn ≤ bn) = ∫ bn an ... ∫ b1 a1 f(x1, . . . , xn)dx1 · · · dxn, 则称 f 为 X 的概率密度函数. Definition Previous Next First Last Back Forward 9