
电路学习指导 第十四章二阶电路 第十四章 二阶电路 一本章要求 1.会建立二阶电路的微分方程:计算二阶电路的零输入响应, 2.掌握振荡、临界振荡与非振荡的概念。 二内容提要 1,二阶电路的零输入响应:换路后没有级里,换路前有初始储能,对C串联电路,描 述电路的方程为:LCd+RC业+M=0. d2 d山 与电路结构参数相关的两个特征根为: R (141) uc Aen Aepy (14-2) A1,A2由初始条件:4c(0,)=lc(0_),iz(0,)=iz(0)所决定。 当风之AA两个不起等的实机,么为载请放电过 当R<2仁时,222为一对共把根,为振荡放电过程 当R=2侵时,月=及=一2公:为事张荡的脑界特况。 R 2.二阶电路的零状态响应:换路后有电源,换路前无初始储能 3.二阶电路的阶跃响应:在单位阶跃函数激励下的零状态响应。 4.二阶电路的冲激响应:在单位冲激函数激励下的零状态响应。 三例题: 例141图141所示的电路中,4c(0)=U。=10P,R=40002,L=1H,C=1F,t0 时,s闭合,求:s闭合后,4c,4R,4L。 13
电路学习指导 第十四章 二阶电路 113 第十四章 二阶电路 一 本章要求 1.会建立二阶电路的微分方程;计算二阶电路的零输入响应。 2.掌握振荡、临界振荡与非振荡的概念。 二 内容提要 1.二阶电路的零输入响应:换路后没有级里,换路前有初始储能,对 RLC 串联电路,描 述电路的方程为: 0 2 2 + + C = C C u dt du RC dt d u LC 。 与电路结构参数相关的两个特征根为: = − − − = − + − L LC R L R p L LC R L R p 1 ) 2 ( 2 1 ) 2 ( 2 2 1 2 1 (14-1) p t p t C u A e A e 1 2 = 1 + 2 (14-2) A1,A2 由初始条件: (0 ) (0 ), (0 ) (0 ) C + = C − L + = L − u u i i 所决定。 当 C L R 2 时, 1 2 p , p 为两个不想等的实根, C u 为非振荡放电过程。 当 C L R 2 时, 1 2 p , p 为一对共轭根, C u 为振荡放电过程。 当 C L R = 2 时, L R p p 2 1 = 2 = − , C u 为非振荡的临界情况。 2.二阶电路的零状态响应:换路后有电源,换路前无初始储能 3.二阶电路的阶跃响应:在单位阶跃函数激励下的零状态响应。 4.二阶电路的冲激响应:在单位冲激函数激励下的零状态响应。 三 例题: 例 14-1 图 14-1 所示的电路中, uC (0− ) = U0 =10V,R = 4000, L =1H,C =1F ,t=0 时,s 闭合,求:s 闭合后, C R uL u ,u ,i,

电路学习指导 第十四章二阶电路 解:2、 2传-210=200L=10H,C=100uF,2>L=10H,C=10F,3>L=25H,C=100F R Us Uc(o) (t) i(o uc(t) (b) 14-2图 114
电路学习指导 第十四章 二阶电路 114 解: R C L = = = − 2000 4000 10 1 2 2 6 , C u 为非振荡放电过程。由(14-1)式有: 2000 2000 10 268, 2000 2000 10 3732 2 6 2 2 6 p1 = − + − = − p = − − − = − 由(14-2) 式有: ( ) , 1 2 1 1 2 2 3732 2 268 1 C p t p t t t C C A p e A p e dt du i C u A e A e = − = − + = + − − 因为 uC (0+ ) = uC (0− ) =10V,i L (0+ ) = i L (0− ) = 0 所以 , 10.774, 0.774 0 10 2 1 1 0 2 2 1 2 0 1 1 1 2 2 1 2 = − − = = − − = + = + = p p p U A p p p U A A p A p A A 从而 u Ri e e V e e V dt di u L i e e mA u e e V t t R t t L t t t t C 11.55( ) 10.774 0.774 2.89( ) 10.774 0.774 , 268 3732 3732 268 268 3732 268 3732 − − − − − − − − = = − = = − = − = − 14-1 图 14-3 图 例 14-2 图 14-1 所示的电路中,电路原来已达到稳态,t=0 时,s 打开,已知: Us =100V,R0 =1K ,求:在下面几种情况下的 u i C , 。 1 L = 10H,C = 100F,2 L = 10H,C = 10F,3 L = 25H,C = 100F 14-2 图

电路学习指导 第十四章二阶电路 解:电路的0等效电路如图142(b) 0)-0)-w0)-0)4R-0a54 UR 当s打开后,电路成为LC串联电路,如图142(c)由(141)式有 1>p=-50+V2500-1000=-1127,P2=-50-V2500-1000=-88.73由(14-2)式 te=he e 有: i=-Cduc=-C(APe Aa P:e) d 所以4+4=50 -C4A+4B)=0.0s4=50.82,4=-0.8198 从而 4e=50.82e-12m-0.8198e7y, i=57.27e-112-7.27e-87mA 2>P,=-50+j86.5,P2=-50-j86.5,6=50,0=86.5由(142)式有: uc Ae-sin(ot+0) i=-cduc =-CAe-#[-6sin(ot+0)+@cos(ot+0)] 1=0,时.4e0.)=50=4smA.0,)=005=-10-5年-50sm0+8660s8l .A=57.74,0=120 所以 4c=57.74es0sm86.6t+120°)Ψ, i1=es0[0.02887sim86.61+120)-0.05cos(86.61+120°】 uc =(A+BI)e- 3)p1=P2=-20由(142)式有: i=-C duc=-CBe*+C8(A+BI)e* 1=0,时,A=50,10(20A-B)=0.05→A=50,B=500 所以c=(50+5001)e207,1=(0.05+t)e2A 15
电路学习指导 第十四章 二阶电路 115 解:电路的 − 0 等效电路如图 14-2(b), A R R U V i i R R U R u u s L L s C (0 ) C (0 ) 50 , (0 ) (0 ) 0.05 0 0 = + = = = + + = − = + − 当 s 打开后,电路成为 RLC 串联电路,如图 14-2(c)由(14-1)式有: 1> p1 = −50 + 2500 −1000 = −11.27, p2 = −50 − 2500 −1000 = −88.73 由(14-2)式 有: ( ) , 1 2 1 1 2 2 88.73 2 11.27 1 C p t p t t t C C A p e A p e dt du i C u A e A e = − = − + = + − − 所以 , 50.82, 0.8198 ( ) 0.05 50 1 2 1 1 2 2 1 2 = = − − + = + = A A C A p A p A A 从而 i e e mA u e e V t t t t C 11.27 88.73 11.27 88.73 57.27 7.27 50.82 0.8198 , − − − − = − = − 2> p1 = −50 + j86.5, p2 = −50 − j86.5, = 50, = 86.5 由(14-2)式有: [ sin( ) cos( )] sin( ) = − = − − + + + = + − − CAe t t dt du i C u Ae t C t t C = 0+ t 时, 0 5 57.74, 120 (0 ) 50 sin , (0 ) 0.05 10 [ 50sin 86.6cos ] = = = = = = − − + − + + A uC A i L A 所以 [0.02887sin( 86.6 120 ) 0.05cos(86.6 120 )] 57.74 sin( 86.6 120 ) , 50 0 0 50 0 = + − + = + − − i e t t u e t V t t C 3〉 p1 = p2 = −20 由(14-2)式有: C t t t C CBe C A Bt e dt du i C u A Bt e − − − = − = − + + = + ( ) ( ) = 0+ t 时, 50,10 (20 ) 0.05 50, 500 4 = − = → = = − A A B A B 所以 u t e V i t e A t t C 20 20 (50 500 ) , (0.05 ) − − = + = +

电路学习指导 第十四章二阶电路 例14-3在图14-3所示的电路中,c(0_)=0,1,(0)=0,=0时,s打开,己知 i,=1A,G=2×103S,C=1F,L=1H,求:阶跃响应c,i 1,1>0 解:s在0时打开,使i,=t)= 0,1R-12 3>R=0三种情况下的零输入响应uc,i。 143s打开前电路已稳定,=0时,s打开,求4c。 14-4电路如图14L,已知:C=2F,L=2.5H,R=1K2,c(0.)=10V,=0时,s闭
电路学习指导 第十四章 二阶电路 116 例 14-3 在图 14-3 所示的电路中, uC (0− ) = 0,i L (0− ) = 0 ,t=0 时,s 打开,已知: i s 1A,G 2 10 S,C 1 F, L 1H 3 = = = = − ,求:阶跃响应 C L u ,i 。 解:s 在 0 时打开,使 = = 0, 0 1, 0 ( ) t t i t s ,所以 s 打开后的响应为解跃响应。 列写方程有: L S L L i i dt di GC dt d i LC + + = 2 2 ,特征方程: 0 2 1 + + = LC p C G p 则: 3 p1 = p2 = p = −10 为二重根,所以对应与方程的齐次解为: pt L i (A A t)e = 1 + 2 , 然而,对应的特解为: i L =1A pt L pt pt pt L A pe A e A te dt di i A A t e 1 2 1 2 2 =1+ ( + ) → = + + 而 uC (0+ ) = uC (0− ) = uL (0+ ) = 0,i L (0+ ) = i L (0− ) = 0 于是: = − = − → − + = = + = = − + + 3 2 1 1 2 0 3 1 10 1 10 0 | 1 0 (0 ) A A dt di A A A i L L 所以 te t V dt di u u L i t e t A L t C L t L 10 ( ) [1 (1 10 ) ] ( ) , 3 3 6 10 3 10 − − = = = = − + 四 习题 14-1 电路如图 14-1,已知: uC (0− ) = 1V C = 1F, L = 1H,R = 4,t=0 时,s 闭合,求: 电路的零输入响应 u i C , 。 14-2 在 14-1 题中,其他参数及初始条件都不变,求:1〉 R = 2 ,2> R =1 3> R = 0 三种情况下的零输入响应 u i C , 。 14-3 s 打开前电路已稳定,t=0 时,s 打开,求 C u 。 14-4 电路如图 14-1,已知: C = 2F, L = 2.5H, R = 1K ,uC (0− ) =10V ,t=0 时,s 闭
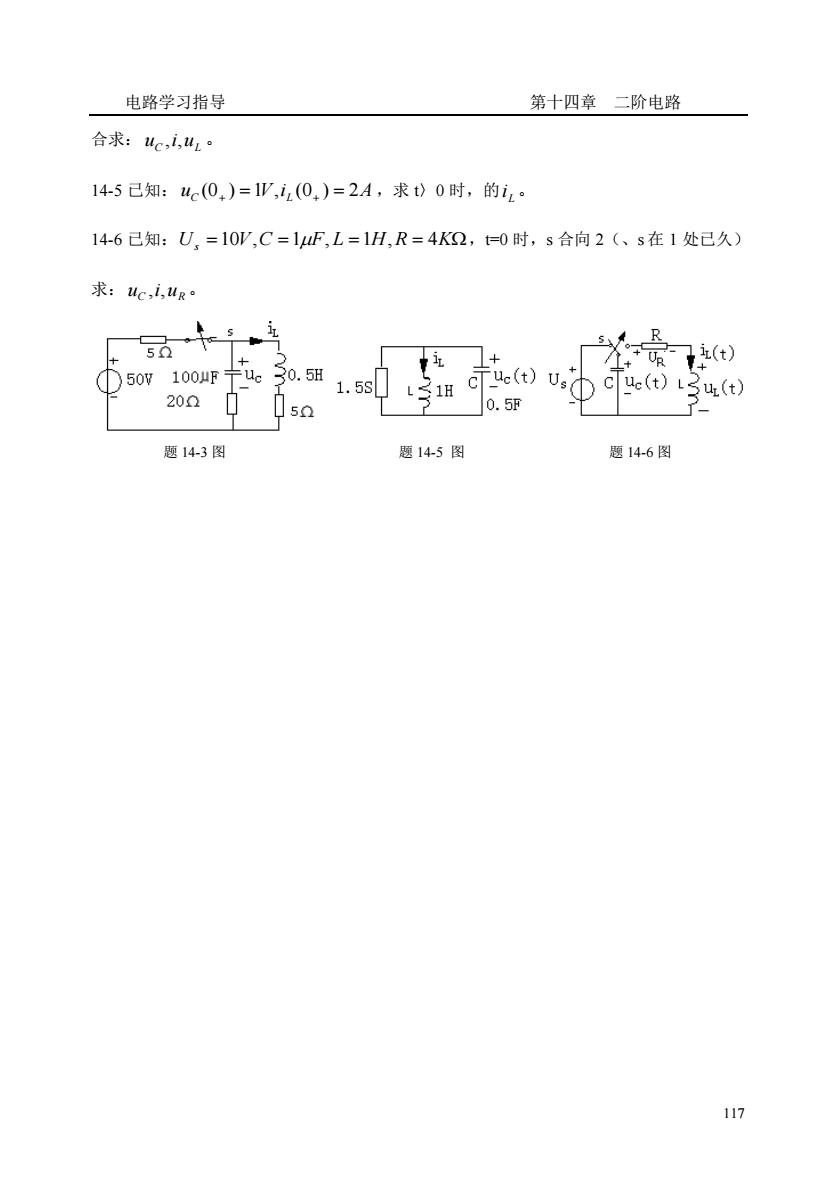
电路学习指导 第十四章二阶电路 合求:uci,L 14-5已知:4c(0,)=1V,(0)=2A,求00时,的i2。 14-6已知:U,=10P,C=1uF,L=1H,R=4K2,0时,s合向2(、s在1处已久) 求:ci,R R (t) 50N100F 0.5 200 1.5s u(t)U uc(t)13u(t) 0.5f 题14-3图 题145图 题14-6图
电路学习指导 第十四章 二阶电路 117 合求: C uL u ,i, 。 14-5 已知: uC (0+ ) =1V,i L (0+ ) = 2A ,求 t〉0 时,的 L i 。 14-6 已知: Us =10V,C =1F, L =1H,R = 4K,t=0 时,s 合向 2(、s 在 1 处已久) 求: C uR u ,i, 。 题 14-3 图 题 14-5 图 题 14-6 图