
电路学习指导 第四章电路定律 第四章 电路定理 一、基本要求 1、本章重点讨论线性网络的一些性质,学生通过学习本章掌握这些性质,有助于学生简 化电路的分析。线性网络最重要的性质就是叠加性,首先我们讨论叠加定理,所以学生 必须掌握叠加定理。 2、熟练掌握有源二端网络的等效电源定理,特别要注意当电路中含有受控源的分析。 3、正确理解互易定理和最大功率的传输定理 二、本章要点 1、叠加定理 在线性电路中,任一支路的电压或电流都可以认为是电路中各个独立源单独作用而其他 独立电源不作用时,在该支路中产生的电压或电流的代数和。 推论:在线性电路中,当所有独立源都增加或缩小K倍时,则响应(电压或电流)也将 同样增大或缩小K倍一齐性定理。 要点: (1)某独立源单独作用时,其他独立源应置零,即若置电压源为零,则用短路代替:若 置电流源为零,则用开路代替。 (2)每个独立源单独作用时,均应保留受控源。 (3)叠加时是求代数和,要注意电压的参考极性、电流的参考方向,即分电路的电压和 电流方向与原电路中所标志的参考方向一致时取“+”,不一致时取“一”。 (4)原电路的功率不等于按各电路计算所得功率的叠加,这是因为功率是电压和电流的 乘积。 (5)叠加定理适用于线性电路,不适用于非线性电路。 2、戴维南定理和诺顿定理 (1)戴维南定理 个由线性电阻,受控源及独立源构成的线性含源一端口网络Ns,对外部电路而言, 可以用一个电压源和一个电阻元件串联组成的等效电路来代替,该电压源的电压等于原 一瑞口网络的开路电压Uo©,该串联电阻就等于将原一端口网络所有独立源置零后所得到 的一端口网络o的等效电阻Rq: (2)诺顿定理 一个线性含源一端口网络Ns,可以用一个电流源和电阻并联组成的等效电路来代替, 该电流源的电流就等于原一端口网络Ns的短路电流,并联电阻与戴维南等效。 要点: ()在应用戴维南定理时,将受控电源和其有控制量的支路不能分开,即线性含源一端口 网络Ns中不能含有控制量在外电路部分的受控源,外电路也不能含有控制量在Ns之中 34
电路学习指导 第四章 电路定律 34 第四章 电路定理 一、基本要求 1、本章重点讨论线性网络的一些性质,学生通过学习本章掌握这些性质,有助于学生简 化电路的分析。线性网络最重要的性质就是叠加性,首先我们讨论叠加定理,所以学生 必须掌握叠加定理。 2、熟练掌握有源二端网络的等效电源定理,特别要注意当电路中含有受控源的分析。 3、正确理解互易定理和最大功率的传输定理 二、本章要点 1、叠加定理 在线性电路中,任一支路的电压或电流都可以认为是电路中各个独立源单独作用而其他 独立电源不作用时,在该支路中产生的电压或电流的代数和。 推论:在线性电路中,当所有独立源都增加或缩小 K 倍时,则响应(电压或电流)也将 同样增大或缩小 K 倍—齐性定理。 要点: (1)某独立源单独作用时,其他独立源应置零,即若置电压源为零,则用短路代替;若 置电流源为零,则用开路代替。 (2)每个独立源单独作用时,均应保留受控源。 (3)叠加时是求代数和,要注意电压的参考极性、电流的参考方向,即分电路的电压和 电流方向与原电路中所标志的参考方向一致时取“+”,不一致时取“一”。 (4)原电路的功率不等于按各电路计算所得功率的叠加,这是因为功率是电压和电流的 乘积。 (5)叠加定理适用于线性电路,不适用于非线性电路。 2、戴维南定理和诺顿定理 (1)戴维南定理 一个由线性电阻,受控源及独立源构成的线性含源一端口网络 NS,对外部电路而言, 可以用一个电压源和一个电阻元件串联组成的等效电路来代替,该电压源的电压等于原 一端口网络的开路电压 U0C,该串联电阻就等于将原一端口网络所有独立源置零后所得到 的一端口网络 N0 的等效电阻 Req。 (2)诺顿定理 一个线性含源一端口网络 Ns,可以用一个电流源和电阻并联组成的等效电路来代替, 该电流源的电流就等于原一端口网络 Ns 的短路电流 isc,并联电阻与戴维南等效。 要点: (1)在应用戴维南定理时,将受控电源和其有控制量的支路不能分开,即线性含源一端口 网络 Ns 中不能含有控制量在外电路部分的受控源,外电路也不能含有控制量在 Ns 之中

电路学习指导 第四章电路定律 的受控源。 (2)这两个定理又合成为等效电源或发电机定理。 (3)该定理特别适用于求解电路中某一条支路的电压或电流。 (4)戴维南等效电路和诺顿定理等效电路可互换 4、互易定理 在线性电路中,仅有一个外施独立电源作用时,则: (1)若独立源为电压源(激励)在某支路A中作用时,在另外一条支路B中所产生的 电流(响应),应等于把该电压源移到支路B是作用而在支路A中所产生的电流。 (2)若独立源为电流愿(激励)在某支路A中作用时,在另外一条支路B中所产生的 开路电压(响应),应等于把该电流源移到支路B中作用而在支路A中所产生的开路电 压。 要点: (1)应用互易定理时,网络中不能包含受控源 (2)激励和响应,一为电压,则另一为电流,或者,一为电流,则另一为电压。 5、最大功率传输定理 当一个含源一端口网络向负载传输功率时,该含源一端口网络传递给负载的功率为 最大的条件是:负载R与含源一端口网络的戴维南(或诺顿)等效电阻Rq相等 满足R=R©q时,称为最大功率匹配,此时,负载吸收的最大功率为: Pmax= 4Req 4 三、典型例题 例4一1,试用叠加原理求图4一1(a)所示电路中的电压U和电流1 5 15 200 20 9 U5 100 (a) (b) (c) 图4一1 例4一1 解:先画出两个电源分别作用时的电路如图(b)和(c)所示。 (1)当3A电流源单独作用时,将9V电压源置零后用短路代替,电路如图(b)所示 35
电路学习指导 第四章 电路定律 35 的受控源。 (2)这两个定理又合成为等效电源或发电机定理。 (3)该定理特别适用于求解电路中某一条支路的电压或电流。 (4)戴维南等效电路和诺顿定理等效电路可互换 4、互易定理 在线性电路中,仅有一个外施独立电源作用时,则: (1)若独立源为电压源(激励)在某支路 A 中作用时,在另外一条支路 B 中所产生的 电流(响应),应等于把该电压源移到支路 B 是作用而在支路 A 中所产生的电流。 (2)若独立源为电流愿(激励)在某支路 A 中作用时,在另外一条支路 B 中所产生的 开路电压(响应),应等于把该电流源移到支路 B 中作用而在支路 A 中所产生的开路电 压。 要点: (1)应用互易定理时,网络中不能包含受控源。 (2)激励和响应,一为电压,则另一为电流,或者,一为电流,则另一为电压。 5、最大功率传输定理 当一个含源一端口网络向负载传输功率时,该含源一端口网络传递给负载的功率为 最大的条件是:负载 RL 与含源一端口网络的戴维南(或诺顿)等效电阻 Req 相等。 满足 RL=Req 时,称为最大功率匹配,此时,负载吸收的最大功率为: Pmax= 4Re q U 2 S 或 Pmax= 4 I Req 2 S 三、典型例题 例 4—1,试用叠加原理求图 4—1(a)所示电路中的电压 U 和电流 I 图 4—1 例 4—1 解:先画出两个电源分别作用时的电路如图(b)和( c)所示。 (1)当 3A 电流源单独作用时,将 9V 电压源置零后用短路代替,电路如图(b)所示

电路学习指导 第四章电路定律 IP= 10 10+5 ×3=2A;U0=5I0=5×2=10V (2)当9V电压源单独作用时,将3A的电流源置零后用开路代替,电路如图(©)所示。 12=- 9 =-0.6A;U2'=512'=5×(-0.6)=-3V 10+5 (3)3A的电流源和9V的电压源共同作用时进行叠加求出U和I U=U14U2'=10+(-3)=7V 1曰1+12=2+(-0.6)=1.4A 例4一2、电路如图4一2(a)所示,其中CCVS的电压受过流过6Q电阻的电流控制, 求电压U3: 6 10I 10I0 10 4A 12 9D10v 49 4 (a) (b) o 图4-2 例4-2图 解:对独立电源来说,当某一个独立电源单独作用时,其它电源的电压或电流都可 以零处理,但受控源应均保留在分电路中。 ()当1OV电压源作用时,4A电流源以开路代替,电路如图(b)所示,则有 IP=1P=69=a U90=-10I0+410=(-10+4)×1=-6V (2)当4A电流源作用时,10V电压源以短路代替,电路如图(c)所示,则有 根据分流公式,有 19=-4+6X4-16A 12=4+I2=4+(-1.6)=2.4A U2=-1012+412=-10×(-1.6)+4×2.4=25.6V (3)4A和10V同时作用时进行叠加求出U, U3=U9+U2=-6+25.6=19.6V 36
电路学习指导 第四章 电路定律 36 I (1) = 10 5 10 + ×3=2A ; U(1)=5I(1)=5×2=10V (2)当 9V 电压源单独作用时,将 3A 的电流源置零后用开路代替,电路如图(c)所示。 I (2) =- 10 5 9 + =-0.6 A ; U(2) =5I(2) =5×(-0.6)= -3V (3)3A 的电流源和 9V 的电压源共同作用时进行叠加求出 U 和 I U=U(1)+U (2) =10+(-3)=7V I=I(1) +I (2) =2+(-0.6)=1.4A 例 4—2、电路如图 4—2(a)所示,其中 CCVS 的电压受过流过 6Ω电阻的电流控制, 求电压 U3。 图 4—2 例 4—2 图 解:对独立电源来说,当某一个独立电源单独作用时,其它电源的电压或电流都可 以零处理,但受控源应均保留在分电路中。 ⑴ 当 10V 电压源作用时,4A 电流源以开路代替,电路如图(b)所示,则有 I (1) 1 = I (2) 1 = 6 4 10 + =1A U (1) 3 =-10 I (1) 1 +4 I (1) 2 =(-10+4)×1=-6V (2)当 4A 电流源作用时,10V 电压源以短路代替,电路如图(c)所示,则有 根据分流公式,有 I (2) 1 =- 4 6 4 + =×4= -1.6A I (2) 1 = 4+ I (2) 1 = 4+(-1.6)=2.4A U (2) 3 = -10 I (2) 1 +4 I (2) 1 = -10×(-1.6)+4×2.4=25.6V (3) 4A 和 10V 同时作用时进行叠加求出 U 3 。 U 3 = U (1) 3 + U (2) 3 =-6+25.6=19.6V
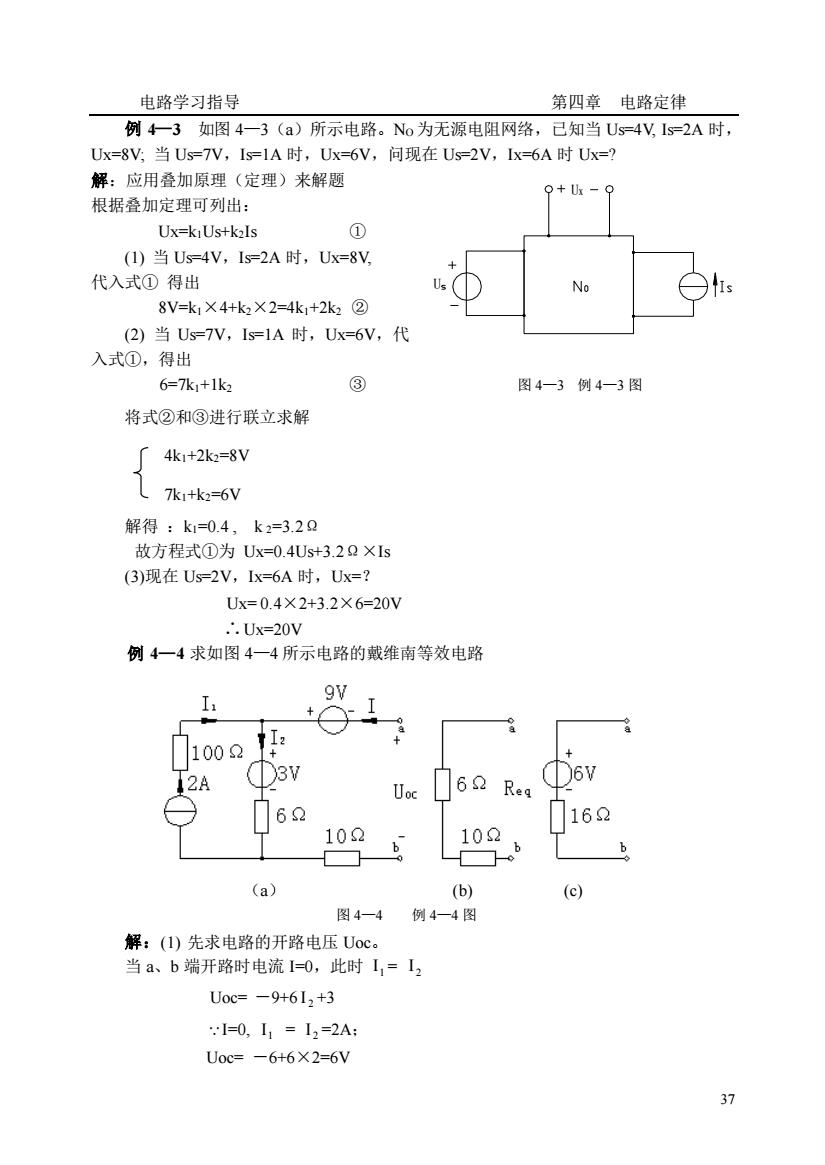
电路学习指导 第四章电路定律 例4一3如图4一3(a)所示电路。No为无源电阻网络,已知当Us-4Vls=2A时, Ux=8V,当Us=7V,Is=1A时,Ux=6V,问现在Us-2V,Ix=6A时Ux=? 解:应用叠加原理(定理)来解题 根据叠加定理可列出: Ux=kiUs+k2Is ① (1)当Us=4V,Is=2A时,Ux=8V 代入式①得出 8V=k1×4+k2×2=4k1+2k2② (2)当Us-7V,Is=1A时,Ux=6V,代 入式①,得出 6=7k1+1k2 @ 图4一3例4一3图 将式②和③进行联立求解 4k1+2k2=8V L7k1+k2=6V 解得:k1=0.4,k2=3.20 故方程式①为Ux=0.4Us+3.20×1s (3)现在Us-2V,Ix=6A时,Ux=? Ux=0.4X2+3.2X6=20V .∴.Ux=20V 例4一4求如图4一4所示电路的戴维南等效电路 gv I 1002 3V D6V Uoc 62 162 102 102 b (a) (b) 图4一4例4一4图 解:()先求电路的开路电压Uoc 当a、b端开路时电流-0,此时I,=I2 Uoc=-9+612+3 l=0,I1=12=2A: U0c=-6+6×2=6V 37
电路学习指导 第四章 电路定律 37 例 4—3 如图 4—3(a)所示电路。NO 为无源电阻网络,已知当 Us=4V, Is=2A 时, Ux=8V; 当 Us=7V,Is=1A 时,Ux=6V,问现在 Us=2V,Ix=6A 时 Ux=? 解:应用叠加原理(定理)来解题 根据叠加定理可列出: Ux=k1Us+k2Is ① (1) 当 Us=4V,Is=2A 时,Ux=8V, 代入式① 得出 8V=k1×4+k2×2=4k1+2k2 ② (2) 当 Us=7V,Is=1A 时,Ux=6V,代 入式①,得出 6=7k1+1k2 ③ 图 4—3 例 4—3 图 将式②和③进行联立求解 4k1+2k2=8V 7k1+k2=6V 解得 :k1=0.4 , k 2=3.2Ω 故方程式①为 Ux=0.4Us+3.2Ω×Is (3)现在 Us=2V,Ix=6A 时,Ux=? Ux= 0.4×2+3.2×6=20V Ux=20V 例 4—4 求如图 4—4 所示电路的戴维南等效电路 (a) (b) (c) 图 4—4 例 4—4 图 解:(1) 先求电路的开路电压 Uoc。 当 a、b 端开路时电流 I=0,此时 1 I = 2 I Uoc= -9+6 2 I +3 I=0, 1 I = 2 I =2A; Uoc= -6+6×2=6V U UX
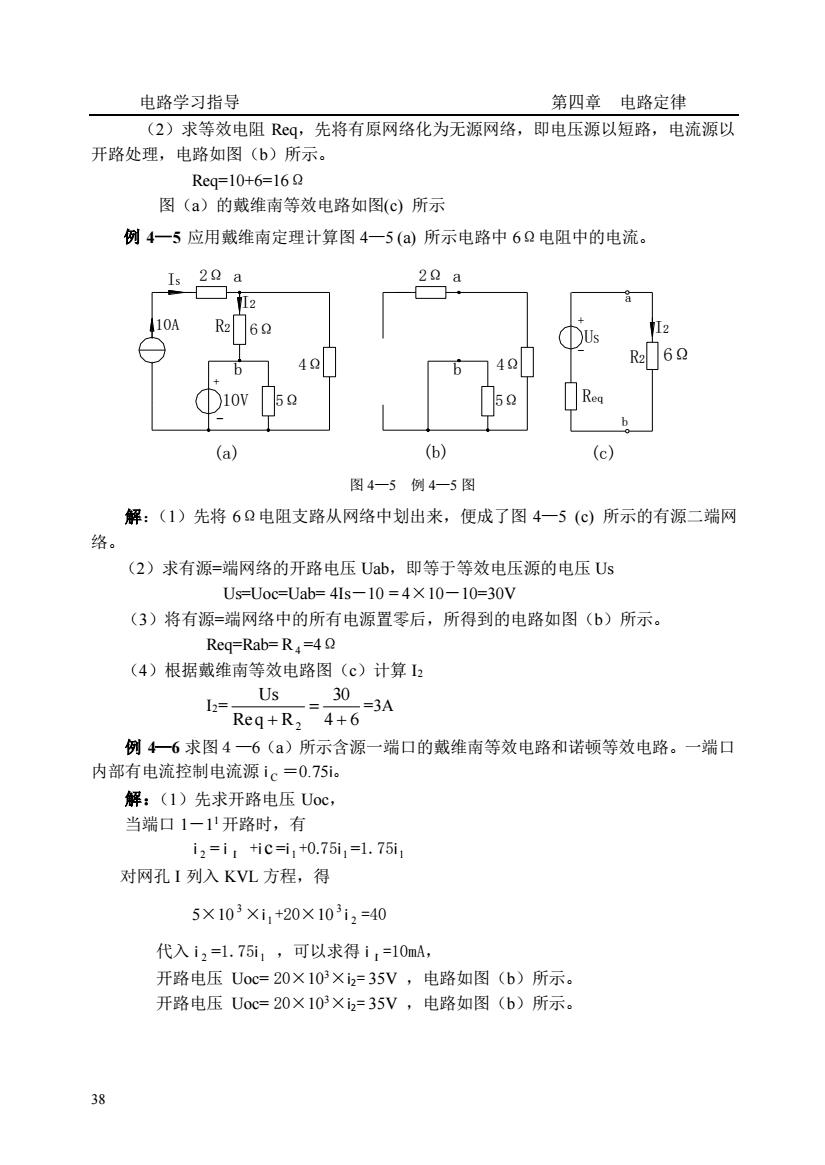
电路学习指导 第四章电路定律 (2)求等效电阻Rq,先将有原网络化为无源网络,即电压源以短路,电流源以 开路处理,电路如图(b)所示。 Req=10+6=16Q 图(a)的戴维南等效电路如图(c)所示 例4一5应用戴维南定理计算图4一5(a)所示电路中6Q电阻中的电流。 Is 20 a 20 a s 6 6 14 ①1ov5 (a) (6) (c) 图4一5例4一5图 解:(1)先将6Q电阻支路从网络中划出来,便成了图4一5(C)所示的有源二端网 络 (2)求有源=端网络的开路电压Ub,即等于等效电压源的电压Us Us=Uoc-Uab=4ls-10=4×10-10-30V (3)将有源=端网络中的所有电源置零后,所得到的电路如图(b)所示。 Req=Rab=R=49 (4)根据戴维南等效电路图(c)计算I 2 Us 30 Req+R:4+6 3A 例4一6求图4一6(a)所示含源一端口的戴维南等效电路和诺顿等效电路。一端口 内部有电流控制电流源1c=0.75i。 解:(1)先求开路电压Uoc 当端口1一1开路时,有 i2=itic=i1+0.75i1=1.75i1 对网孔I列入KVL方程,得 5×103×1,+20×10312=40 代入12=1.75i,可以求得i,=10mA, 开路电压Uoc=20×103×i2=35V,电路如图(b)所示。 开路电压Uoc=20×103×i2=35V,电路如图(b)所示
电路学习指导 第四章 电路定律 38 (2)求等效电阻 Req,先将有原网络化为无源网络,即电压源以短路,电流源以 开路处理,电路如图(b)所示。 Req=10+6=16Ω 图(a)的戴维南等效电路如图(c) 所示 例 4—5 应用戴维南定理计算图 4—5 (a) 所示电路中 6Ω电阻中的电流。 图 4—5 例 4—5 图 解:(1)先将 6Ω电阻支路从网络中划出来,便成了图 4—5 (c) 所示的有源二端网 络。 (2)求有源=端网络的开路电压 Uab,即等于等效电压源的电压 Us Us=Uoc=Uab= 4Is-10 = 4×10-10=30V (3)将有源=端网络中的所有电源置零后,所得到的电路如图(b)所示。 Req=Rab= R4 =4Ω (4)根据戴维南等效电路图(c)计算 I2 I2= 4 6 30 Req R Us 2 + = + =3A 例 4—6 求图4—6(a)所示含源一端口的戴维南等效电路和诺顿等效电路。一端口 内部有电流控制电流源 i C =0.75i。 解:(1)先求开路电压 Uoc, 当端口 1-1 1 开路时,有 i 2 = i 1 +i c =i 1 +0.75i 1 =1.75i 1 对网孔 I 列入 KVL 方程,得 5×10 3 ×i 1 +20×10 3 i 2 =40 代入 i 2 =1.75i 1 ,可以求得 i 1 =10mA, 开路电压 Uoc= 20×103×i2= 35V ,电路如图(b)所示。 开路电压 Uoc= 20×103×i2= 35V ,电路如图(b)所示。 10A (a) + 10V - b 4Ω 5Ω (b) 5Ω b 4Ω I2 6Ω IS 2Ω R2 a 2Ω a US R2 (c) Req - b 6Ω + a I2
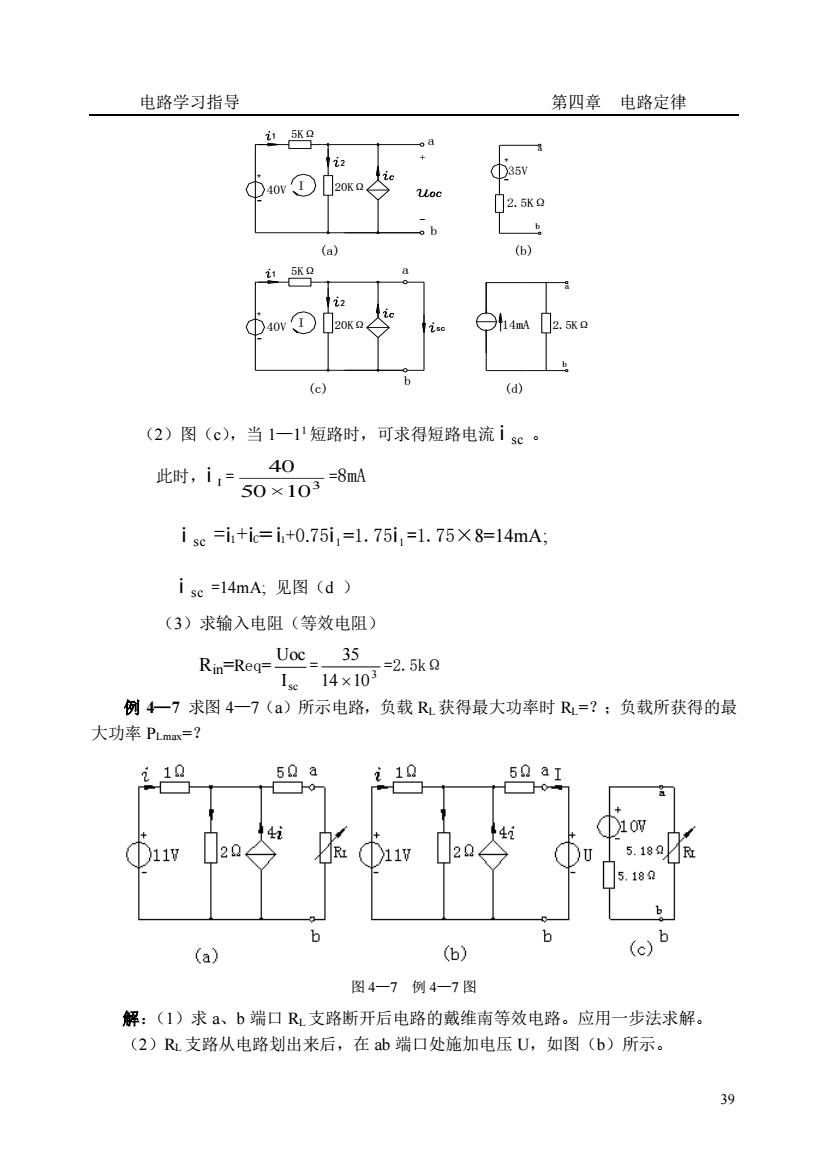
电路学习指导 第四章电路定律 540v①2oK0 25 c (d) (2)图(c),当1一1'短路时,可求得短路电流isc。 40 此时.i50108ad isc=i+i=i+0.75i,=1.75i,=l.75×8=14mA isc=l4mA;见图(d) (3)求输入电阻(等效电阻) Rn-Req-Uoc35 Ic14×103 =2.5k0 例4一7求图4一7()所示电路,负载R获得最大功率时R=?:负载所获得的最 大功率PLm=? 10 50a 10 50 aI 4 )11 20 11 204 DU 5.18 5.18 (a) (6) (c)6 图4-7例4-7图 解:(I)求a、b端口R支路断开后电路的戴维南等效电路。应用一步法求解。 (2)R支路从电路划出来后,在b端口处施加电压U,如图(b)所示。 39
电路学习指导 第四章 电路定律 39 (2)图(c),当 1—1 1 短路时,可求得短路电流 i sc 。 此时,i 1 = 3 50×10 40 =8mA i sc =i1+iC= i1+0.75i 1 =1.75i 1 =1.75×8=14mA; i sc =14mA; 见图(d ) (3)求输入电阻(等效电阻) Rin=Req= sc I Uoc = 3 14 10 35 =2.5kΩ 例 4—7 求图 4—7(a)所示电路,负载 RL 获得最大功率时 RL=?;负载所获得的最 大功率 PLmax=? 图 4—7 例 4—7 图 解:(1)求 a、b 端口 RL 支路断开后电路的戴维南等效电路。应用一步法求解。 (2)RL 支路从电路划出来后,在 ab 端口处施加电压 U,如图(b)所示。 (c) b 2 2 20KΩ 20KΩ - 40V 1 - + I 5KΩ (a) 1 40V + 5KΩ I a sc b - a + (d) b 2.5KΩ 14mA 2.5KΩ (b) b a 35V - + a

电路学习指导 第四章电路定律 (3)求电压U和电流I之间的关系。 根据KVL得: U=51+21+4i+i)=7I+10i 1-(0-5D=11-1SX+5I 12 代入上式得出 U=71+10(11-U+51) 110=571+110 U=5.181+10 由上式U=Us一I,可直接得出戴维南等效电路中电压源电压为I0V,串联等效内阻为 5.180 (4)作出等效电路如图(c)所示,可知负载获得最大功率时的电阻值为: RL=Req=5.18Q (5)负载所获得的最大功率为 U3102 P1m4Rs4x5.18=438w 例4一8如图4一8(a)所示电路,试应用互易定理,求电流1。 20 40 129 29 I 10 门20D8w 图4一8例4一8图 解:(1)为了简化计算,应用互易定理来求解比较方便。 (2)根据互易定理,8V电压源在ab支路作用时,cd支路中产生的电流I,相当 于电压源在cd支路作用时,b支路中产生的电流I,如图4一8(b)所示电路。在图(b) 电路中: 8 8 2+4x2+1x2 (3)按分流公式可得出 40
电路学习指导 第四章 电路定律 40 (3)求电压 U 和电流 I 之间的关系。 根据 KVL 得: U=5I+2(I+4i+i)=7I+10i ∵i= − − 1 11 (U 5I)=11-1S×U+5I 代入上式得出 U=7I+10(11-U+5I) 11U=57I+110 U=5.18I+10 由上式 U=Us-RI,可直接得出戴维南等效电路中电压源电压为 10V,串联等效内阻为 5.18Ω (4)作出等效电路如图(c)所示,可知负载获得最大功率时的电阻值为: RL=Req=5.18Ω (5)负载所获得的最大功率为 P L max = 4.38w 4 5.18 10 4Rs U 2 2 S = = ; 例 4—8 如图 4-8(a)所示电路,试应用互易定理,求电流 I 。 图 4—8 例 4—8 图 解:(1)为了简化计算,应用互易定理来求解比较方便。 (2)根据互易定理,8V 电压源在 ab 支路作用时,cd 支路中产生的电流 I,相当 于电压源在 cd 支路作用时,ab 支路中产生的电流 I,如图 4-8(b)所示电路。在图(b) 电路中: I1= 2A 3 2 3 4 2 8 1 2 1 2 4 2 4 2 2 8 = + + = + + + + (3)按分流公式可得出 I2 = A 3 2 2 3 1 I 1 2 1 1 = = +

电路学习指导 第四章电路定律 3= 2x2-A 4 根据KCL,便可得出所求电流为 -号A 故求出图4一8(a)电路中的电流卡号A 41
电路学习指导 第四章 电路定律 41 I3 = A 3 4 2 3 1 I 41 2 4 1 = = + 根据 KCL,便可得出所求电流为 I= I3-I2= A 3 2 3 2 3 4 − = 故求出图 4—8(a)电路中的电流 I= A 3 2

电路学习指导 第四章电路定律 四.习题 4一1用叠加定理计算图4一1(a)(b)所示的二电路的电流1x和电压Uy。 ①6 129 20 2K 6A ,109 (a) (6) 题4-1图 4一2用叠加定理求图4一2所示电路的电压Ux 4一3图4一3中N表示线性电阻无源网络,若1s1=8A,1=12A,则Ux=80V 若Is1=一8A,Is2=4A则,求当Ux=0V,求当Is1=Is2=20A时,Ux是多少? No 10w 题4-2图 题4-3图 4一4应用叠加定理求出图示电路中电压U。 4一5叠加定理求解图4一5所示含受控源的电路,即求儿。 ①A 题4一4图 题4一5图 4-6如图4-6所示电路,求电压U。 4-7应用叠加定理求图4-7示电路中的电压U 42
电路学习指导 第四章 电路定律 42 四.习题 4—1 用叠加定理计算图 4—1(a)(b)所示的二电路的电流 IX 和电压 Uy。 题 4-1 图 4—2 用叠加定理求图 4—2 所示电路的电压 Ux 4—3 图 4—3 中 N 表示线性电阻无源网络,若 IS1= 8A ,IS2= 12A,则 UX=80V ; 若 IS1=-8A ,IS2= 4A 则,求当 UX=0V,求当 IS1= IS2= 20A 时,UX 是多少? 题 4-2 图 题 4-3 图 4—4 应用叠加定理求出图示电路中电压 U 。 4—5 叠加定理求解图 4—5 所示含受控源的电路,即求 UX。 题 4—4 图 题 4—5 图 4-6 如图 4-6 所示电路,求电压 U。 4-7 应用叠加定理求图 4-7 示电路中的电压 U 4V 6V 2Ω 2Ω (b) 2KΩ Uy (a) 1KΩ - 2KΩ - 6A + - 2A 10Ω + IX + + - 10V 6Ω 4Ω 5A UX 2Ω - IS1 8Ω + N0 IS2 + UX -
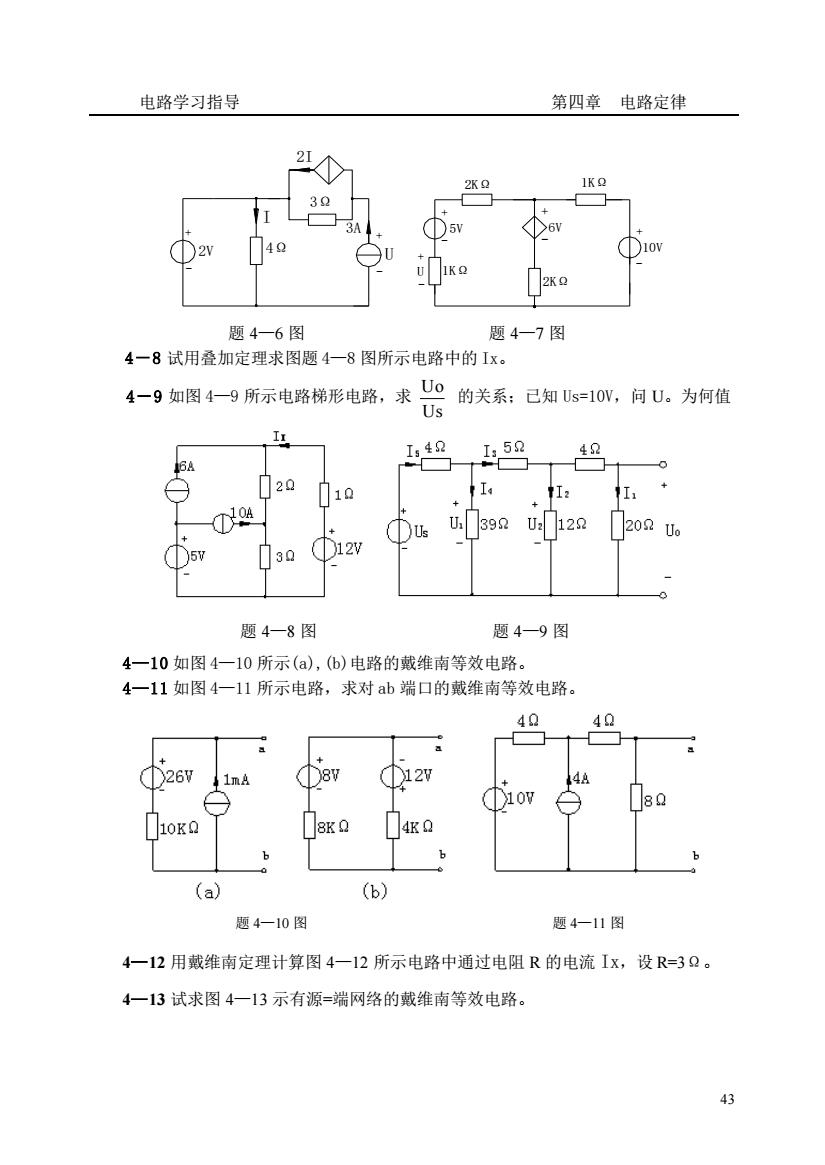
电路学习指导 第四章电路定律 20 题4一6图 题4一7图 4一8试用叠加定理求图题4一8图所示电路中的1x。 4-9如图4一-9所示电路梯形电路,求U0的关系:已知Us=1O,问U。为何值 Us I:50 42 20 10 tI: U39U122 30 题4一8图 题4一9图 4一10如图4一10所示(a),(b)电路的戴维南等效电路。 4一11如图4一11所示电路,求对ab端口的戴维南等效电路。 40 40 2元 10m 10K0 好0 Q (a) (b) 题4一10图 题4-11图 4一12用戴维南定理计算图4一12所示电路中通过电阻R的电流Ix,设R=3Q 4一13试求图4一13示有源=端网络的戴维南等效电路。 43
电路学习指导 第四章 电路定律 43 题 4—6 图 题 4—7 图 4-8 试用叠加定理求图题 4—8 图所示电路中的 Ix。 4-9 如图 4—9 所示电路梯形电路,求 Us Uo 的关系;已知 Us=10V,问 U。为何值 题 4—8 图 题 4—9 图 4—10 如图 4—10 所示(a),(b)电路的戴维南等效电路。 4—11 如图 4—11 所示电路,求对 ab 端口的戴维南等效电路。 题 4—10 图 题 4—11 图 4—12 用戴维南定理计算图 4—12 所示电路中通过电阻 R 的电流 Ix,设 R=3Ω。 4—13 试求图 4—13 示有源=端网络的戴维南等效电路。 3Ω 2V 4Ω - + I 3A 2I + 2KΩ 5V 6V 1KΩ U - U - + + - + - 10V - + 2KΩ 1KΩ