
电路学习指导 第十六章网络函数 第十六章网络函数 一本章要求 1.握网络函数的物理意义及极、零点的概念。 2.画及、零点分布图并理解及、零点分布与时域解的关系。 3.掌握卷积概念并进行简单计算 二内容提要 1.网路函数定义:H)= (16-1) E(s) R(S)是零状态响应的像函数,E(S)是激励的像函数。 2.单位冲激响应h()=L[H(s] (16-2) 3.将网络函数表示成:H(S)=H。 f1-) (16-3) s-p,) 其中,二,i=1,2,.m称作H(s)的零点:p,j=1,2,.n称作H(s)的极点。在复平面上, 用“。”表示零点,用“×”表示极点,则得到网络函数的零、极点分布图。 4.当为真分时且具有单根时,0=Ke” (16-4) 则:H(s)的极点在s的左半平面,()随着t的增加而衰减,电路稳定。H(s)的极点在s的 右半平面,ht)随着t的增加而增加,电路不稳定。H(s)的极点在虚轴上,h()将是纯正弦 量。 5.频率响应函数:HS)=H(s)o=HUo∠Uo) (16-5) 称:Hjo~o曲线为幅频特性,(o)~o相频特性。 三例题 例1614,)是激励,L=1.5H,L2=0.5H,R=12,C,=F,,求电压转移函数 H,=,@和驱动电导纳函数H,(=@ U,(s) U,(s)
电路学习指导 第十六章 网络函数 128 第十六章 网络函数 一 本章要求 1. 握网络函数的物理意义及极、零点的概念。 2. 画及、零点分布图并理解及、零点分布与时域解的关系。 3. 掌握卷积概念并进行简单计算。 二 内容提要 1.网络函数定义: ( ) ( ) ( ) E s R s H s = (16-1) R(s)是零状态响应的像函数,E(s)是激励的像函数。 2.单位冲激响应 ( ) [ ( )] 1 h t L H s − = (16-2) 3.将网络函数表示成: = = − − = n j j m i i s p s z H s H 1 1 0 ( ) ( ) ( ) (16-3) 其中, zi ,i = 1,2, m 称作 H(s)的零点; p j , j = 1,2, n 称作 H(s)的极点。在复平面上, 用“o”表示零点,用“x”表示极点,则得到网络函数的零、极点分布图。 4.当 H(s)为真分时且具有单根时, = = n i p t i i h t K e 1 ( ) (16-4) 则:H(s)的极点在 s 的左半平面,h(t)随着 t 的增加而衰减,电路稳定。H(s)的极点在 s 的 右半平面,h(t)随着 t 的增加而增加,电路不稳定。H(s)的极点在虚轴上,h(t)将是纯正弦 量。 5. 频率响应函数: ( ) ( ) ( ) ( ) H s H s H j j = s= j = (16-5) 称: H( j) ~ 曲线为幅频特性, ( j) ~ 相频特性。 三 例题 例 16-1 ( ) 1 u t 是激励, L H L H R C F 3 4 1.5 , 0.5 , 1 , 1 = 2 = = 2 = ,求电压转移函数 ( ) ( ) ( ) 1 2 1 U s U s H s = 和驱动电导纳函数 ( ) ( ) ( ) 1 1 2 U s I s H s =

电路学习指导 第十六章网络函数 1 1,s)=U 解:给定电路的运算电路如161(b)则: sC2 1 +R)12(s)=0 SC -I(s)+(sL3+ sC2 则: 10=4C+8C,s+U,(s.1,国= D(s) 间.w-:o 1 2s2+4s+3 ∴.H,(s)= +22+25+T月,() 3(s3+2s2+2s+1) 例16-2绘出H(s)= 家、服 解: N(s)=2(s-2s-4),∴31=2,22=4 则:零、极点分布图如图16-2 I(s)aL 2 ua(t)R Us) 424→ (a) (b) 图16-1例16-1图 图16-2例16-2图 例163求HS)=,③且画出幅频特性及相频特性曲线。 U(s) 1+1+s)U(s)-U2(s)=U,(s) 解: ,所以: -U(s)+1+s)U2(s)=0 1 )-2+X+HU@)-2+joX1+jo-1-+0 幅频特性及相频特性曲线分别如图16-3(b)、(c)所示。可见,此网络为一个低通滤波器 129
电路学习指导 第十六章 网络函数 129 解:给定电路的运算电路如 16-1 (b)则: − + + + = + − = ) ( ) 0 1 ( ) ( 1 ( ) ( ) 1 ) ( ) 1 ( 2 2 1 3 2 2 1 2 1 2 R I s sC I s sL sC I s U s sC I s sC sL , 则: 3( 2 2 1) 2 4 3 , ( ) 2 2 1 1 ( ) ( ), ( ) ( ) ( ) 1 ( ), ( ) ( ) 1 ( ) 3 2 2 1 3 2 2 1 2 1 2 2 3 2 2 1 + + + + + = + + + = = = + + = s s s s s H s s s s H s U s U s RI s D s U s I s D s L C s RC s I s 例 16-2 绘出 4 6 3 2 12 16 ( ) 3 2 2 + + + − + = s s s s s H s 的零、极点图。 解: 2 3 2 3 , 2 3 2 3 1, ) 2 3 2 3 )( 2 3 2 3 ( ) ( 1)( ( ) 2( 2)( 4), 2, 4 1 2 3 1 2 p p j p j D s s s j s j N s s s z z = − = − − = − + = + + + + − = − − = = 则:零、极点分布图如图 16-2 图 16-1 例 16-1 图 图 16-2 例 16-2 图 例 16-3 求 ( ) ( ) ( ) 2 U s U s H s = 且画出幅频特性及相频特性曲线。 解: − + + = + + − = ( ) (1 ) ( ) 0 (1 1 ) ( ) ( ) ( ) 2 2 1 U s s U s s U s U s U s , 所以: 1 3 1 (2 )(1 ) 1 1 , ( ) (2 )(1 ) 1 1 ( ) 2 j j j H j s s H s − + = + + − = + + − = 幅频特性及相频特性曲线分别如图 16-3 (b)、(c)所示。可见,此网络为一个低通滤波器

电路学习指导 第十六章网络函数 1 0123 11 -90 07 12 180 (a) (b) (e) 图16-3例16-3图 例16-4已知:R=500K2,C=1uF,i,()=2eA,设点容上原来没有电压,求:4c(t)。 R,(s)1 1 1 解,方法一:H)=U( R I.(s) 1(s) sC+1= c -1x10 1 *RC 3+2 Eo=1o=104 所以:c(=Hs1,s)= 22 R +13+2 wc()=(2e'-2e2)Ψ,1≥0 图16-4例16-4 四习题 5+10 161已知:H)=g+209十500求:K0.并国极.零点分布图 16-2已知:H()=,-O3求:h0.并画极、零点分布图及h0的波形。 63已知:LH.C=2PR=12飞=22,求:H6)光及其极、专点图 16-4网络的单位阶跃响应为:1-e,则H(s)=? 16-5定性分析图示电路中以4,为输出时的频率响应。 16-6求策动电导纳。 习题答案 16-1h0=e10c0s20,P2=-10±j20 130
电路学习指导 第十六章 网络函数 130 图 16-3 例 16-3 图 例 16-4 已知: R K C F i t e A t s − = 500 , = 1 , ( ) = 2 ,设点容上原来没有电压,求: u (t) C 。 解: 方法一: 2 1 10 1 1 1 ( ) 1 1 1 ( ) ( ) ( ) ( ) 6 + = + = + = + = = − s RC s C sRC R I s sC sC R RI s I s U s H s s s s C A s E s I s s 6 10 1 2 ( ) ( ) − + = = 所以: ( ) (2 2 ) , 0 , 2 2 1 2 ( ) ( ) ( ) 2 = − + − + = = − − u t e e V t s s U s H s I s t t C C s 图 16-4 例 16-4 四 习题 16-1 已知: 20 500 10 ( ) 2 + + + = s s s H s ,求:h(t)。并画极、零点分布图。 16-2 已知: 0.3 2 ( ) − = s H s ,求:h(t)。并画极、零点分布图及 h(t)的波形。 16-3 已知: L =1H,C = 2F,R1 =1,R2 = 2 ,求: ( ) ( ) ( ) 2 U s U s H s = 及其极、零点图。 16-4 网络的单位阶跃响应为: t e − 1− ,则 H(s)=? 16-5 定性分析图示电路中以 2 u 为输出时的频率响应。 16-6 求策动电导纳。 习题答案 16-1 ( ) cos20 , 1,2 10 20 10 h t e t p j t = = − −
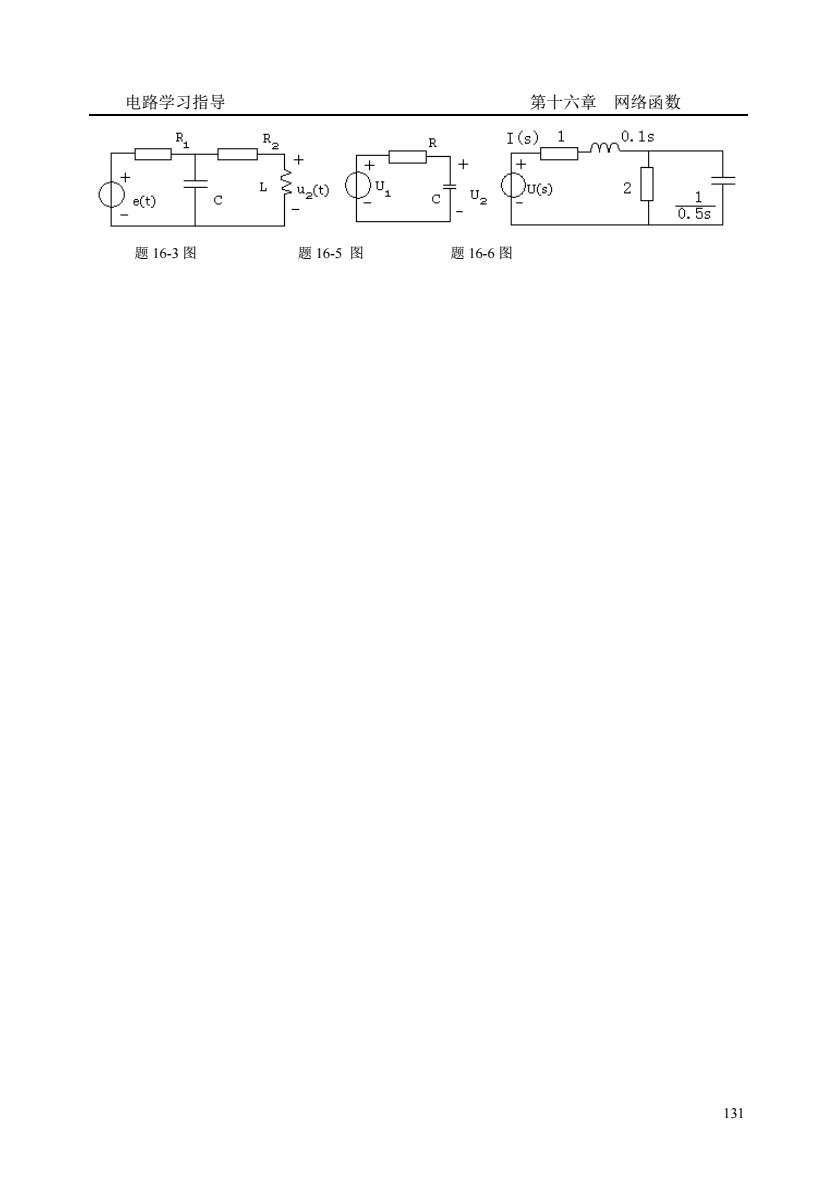
电路学习指导 第十六章网络函数 w。w ①u()2 题16-3图 题16-5图 题16-6图 131
电路学习指导 第十六章 网络函数 131 题 16-3 图 题 16-5 图 题 16-6 图