
电路学习指导 第六章非线性电阻电路 第六章 非线性电阻电路 一、基本要求 1、非线性电阻电路是在学完线性电路的基础上进行的。因此,应注意与线性电路的共同 点之外,还要特别注意它与线性电路分析方法的不同点。 2、重点掌握非线性元件的特性,正确编写非线性电路的方程 3、要掌握简单非线性电阻电路的图解法及小信号分析法,其中小信号分析法在以后的电 子线路里应用非常广泛,因此,要求重点掌握小信号法分析法。 二、本章要点 1、非线性电阻的定义 凡电压电流的关系在一平面上不是过原点的直线的电阻元件,称为非线性电阻。 2、非线性电阻组特性的多值性 (1)电流控制型(流控型)非线性电阻u=f() (2)电压控制型(压控型)非线性电阻i=g() (3)单调型非线性电阻,即可表示为“=f)(流控型)又可表示为是i=g(,)(压 控型),且它们互为反函数,即间=g(, 非线性电阻通常引用静态电阻R=h和动态电阻R。=du体的概念。 3、非线性电路的分析方法 (1)小信号分析法的实质是在静态工作电处将非线性电阻的特性直线来近似(线性化)。 (2)分段线性化法是将非线性电路的分析变为若干个线性电路来计算的方法。 三、典型例题 例6一1在图6一1所示的电路中,己知U。=20W,4s1)=snW,R=12 非线性电阻的伏安特性为“=?求电流1。 解:小信号分析法来求解。首先求工作点,因为给定的非线性电阻特性的解析式比较 简单,所以不必采用图解法来进行求解。 当4s1)=0时, 根据KL,有U。=RIo+Ug 以数据及伏安特性代入 16+16-20=0 10=44 解得 图6-1例6-1图 Uo=16=16M
电路学习指导 第六章 非线性电阻电路 50 第六章 非线性电阻电路 一、基本要求 1、非线性电阻电路是在学完线性电路的基础上进行的。因此,应注意与线性电路的共同 点之外,还要特别注意它与线性电路分析方法的不同点。 2、重点掌握非线性元件的特性,正确编写非线性电路的方程。 3、要掌握简单非线性电阻电路的图解法及小信号分析法,其中小信号分析法在以后的电 子线路里应用非常广泛,因此,要求重点掌握小信号法分析法。 二、本章要点 1、非线性电阻的定义 凡电压电流的关系在 u-i 平面上不是过原点的直线的电阻元件,称为非线性电阻。 2、非线性电阻组特性的多值性 (1)电流控制型(流控型)非线性电阻 u = f (i) (2)电压控制型(压控型)非线性电阻 i = g(u) (3)单调型非线性电阻,即可表示为 u = f (i) (流控型) 又可表示为是 i = g(u) (压 控型),且它们互为反函数,即 f(i)=g-1 (u) 。 非线性电阻通常引用静态电阻 R=u/i 和动态电阻 Rd =du/di 的概念。 3、非线性电路的分析方法 (1)小信号分析法的实质是在静态工作电处将非线性电阻的特性直线来近似(线性化)。 (2)分段线性化法是将非线性电路的分析变为若干个线性电路来计算的方法。 三、典型例题 例 6— 1 在图 6—1 所示的电路中,已知 U 20V , 0 = u (t ) sin tV , S = R = 1 非线性电阻的伏安特性为 2 u = i 求电流 i 。 解:小信号分析法来求解。首先求工作点,因为给定的非线性电阻特性的解析式比较 简单,所以不必采用图解法来进行求解。 当 uS (t ) = 0 时, 根据 KVL,有 U0 = RIQ +UQ 以数据及伏安特性代入 I IQ 20 0 2 Q + − = 解得 U I 16V I 4A; 2 Q Q Q = = = 图 6-1 例 6-1 图

电路学习指导 第六章非线性电阻电路 (I。的另一个解签-5A应舍去) 工作点处的动志电图为风-引-=2阳 由小信号电压4s()加入作用下,电路中电流的增量 -%器-nd 电路中的电流i的全解为1=e+M=(4+号m)A: 现在来看一下,用小信号分析法来求解本例究竞会多少的误差。为此,应当假设小信 号电压达最大值时来分析,即令山=少,非线性电阻上的总电压为,电流为',则根 据KVL,有: Uot us =Ri'+u' 代入数据,可得20+1=()2+ (t)2+1-21=0 解得:1=4.11A(另一解为一5.11A应舍去) 这个解答是真实解,而用小信号分析法的解是1=4+9=4111A,故相对误差为 B=41-4x10%-0.02433% 4.11 可见,用小信号分析法来分析非线性电路所带来的误差是很小的,完全能满足工程上的要 求。 例6一2电路如图6一2所示,其中非线性电阻的伏安关系为4=20。试列出电路 方程。 解:各电阻的VCR关系为: i:+t- 41=R t 7z 25 42=R2 43=20 然后,根据C和KVL,有: i=i2+i3 图6一2例6一2图 %+42=Us 42=43 51
电路学习指导 第六章 非线性电阻电路 51 ( Q I 的另一个解签 -5A 应舍去) 工作点处的动态电阻为 = = = = = 2i = = 8 di d(i ) di du R i 4 i 4 2 d i 4 由小信号电压 u (t ) S 加入作用下,电路中电流的增量 sintA 9 1 1 8 sint R R u (t ) i d S = + = + = 电路中的电流 i 的全解为 sint )A; 9 1 i = IQ + i =( 4 + 现在来看一下,用小信号分析法来求解本例究竟会多少的误差。为此,应当假设小信 号电压达最大值时来分析,即令 uS = 1V ,非线性电阻上的总电压为 u ,电流为 i ,则根 据 KVL,有: U0+ uS = Ri + u 代入数据,可得 20+1=(i ) i 2 + (i ) i 21 0 2 + − = 解得: i = 4.11A (另一解为 —5.11A 应舍去) 这个解答是真实解,而用小信号分析法的解是 i = 4 + 1 9 = 4.111A,故相对误差为 β= 4.11 4.111− 4.1 ×100%=0.02433% 可见,用小信号分析法来分析非线性电路所带来的误差是很小的,完全能满足工程上的要 求。 例 6—2 电路如图 6-2 所示,其中非线性电阻的伏安关系为 2 1 3 3 u = 20i 。试列出电路 方程。 解:各电阻的 VCR 关系为: 2 1 3 3 2 2 2 1 1 1 u 20i u R i u R i = = = 然后,根据 KCL 和 KVL,有: 图 6-2 例 6-2 图 2 3 1 2 S 1 2 3 u u u u U i i i = + = = +

电路学习指导 第六章非线性电阻电路 从而可得到电路方程为: Rji+R2iz =Us Rh2=207 i1=i3+3 [(R)+R3 )i;-R;is =Us 或者合并为 (R4-R4,-2m=0 例6一3写出如图6一3所示电路的结点电压方程,假设电路中各非线性电阻的伏安特 性为,=,2=.3=4。 解:图中各非线性电阻均为压控型,很方便列写结 12A 点的KCL方程。 it2=12 -6+i6=4 将非线性电阻的伏安关系代入以上KCL方程,且考虑到 ue=u-山得 图6-3例6-3图 u3+(u1-u3)2=12 -(u1-u3)2+up=4 例6一4如图64所示电路中,直流电流源1。=10A,R。=/32非线性电阻为电压控 制型,其伏安特性如图6一4(b)所示,用函数表示为 rau- 小信号电流源is(1)=0.5cos4。试求 (a) 工作点和在工作点处由小信号产生的 电压和电流。 解:应用KCL,有 元+i=+ (c) 或 3u+g(u)=10+0.5cost 图6-4例6-4图 令is=0由上式得 3u+gu)=10 52
电路学习指导 第六章 非线性电阻电路 52 从而可得到电路方程为: 1 2 3 2 1 2 2 3 1 1 2 2 S i i i R i 20i R i R i U = + = + = 或者合并为 − − = + − = R i R i 20i 0 ( R R )i R i U 2 1 2 1 2 3 3 1 2 1 2 3 S 例 6—3 写出如图 6—3 所示电路的结点电压方程,假设电路中各非线性电阻的伏安特 性为 3 2 3 3 2 2 2 3 i 1 = u1 ,i = u ,i = u 。 解:图中各非线性电阻均为压控型,很方便列写结 点的 KCL 方程。 i1+ i2 = 12 -i2+ i3 = 4 将非线性电阻的伏安关系代入以上 KCL 方程,且考虑到 u2 = u1-u3 得 图 6-3 例 6-3 图 ( ) 4 ( ) 12 3 2 3 2 1 3 2 1 3 3 1 + = + = u u u u u u — — — 例 6—4 如图 6—4 所示电路中,直流电流源 I 0 = 10A,R0 = 1 3 非线性电阻为电压控 制型,其伏安特性如图 6—4(b)所示,用函数表示为 ( ) ( ) = = 0 u 0 u u 0 i g( u ) 2 小信号电流源 i S (t ) = 0.5costA 。试求 工作点和在工作点处由小信号产生的 电压和电流。 解:应用 KCL,有 0 S 0 u i I i R 1 + = + 或 3u + g(u ) = 10 + 0.5cost 图 6-4 例 6-4 图 令 i S = 0 由上式得 3u + g(u ) = 10

电路学习指导 第六章非线性电阻电路 把g(u)=2(u>0)代入上式并求解所得方程,可得对应工作点的电压U。=2 ,1。=4A。工作点处的动态电导为 G,dg(u) =品n=24=s 作出小信号等效电路如图6一3(©)所示,从而求出非线性电阻的小信号电压和电流为: wcost -0.07lcosp 1=号cos1=0.286cos4 电路的全解,亦即非线性电阻的电压、电流为: u=Uo+4=(2+0.0714cos1W i=10+i=(4+0.286cost4 53
电路学习指导 第六章 非线性电阻电路 53 把 ( ) ( 0) 2 g u = u u 代入上式并求解所得方程,可得对应工作点的电压 UQ = 2V ,IQ = 4A 。工作点处的动态电导为 (u ) 2u 4S du d du dg(u ) G U 2 2 d UQ Q = = = = = 作出小信号等效电路如图 6—3(c)所示,从而求出非线性电阻的小信号电压和电流为: cost 0.071costV 7 0.5 u1 = = cost 0.286costA 7 2 i 1 = = 电路的全解,亦即非线性电阻的电压、电流为: i I i ( 4 0.286cost )A u U u 2 0.0714cost )V Q 1 Q 1 = + = + = + =( +
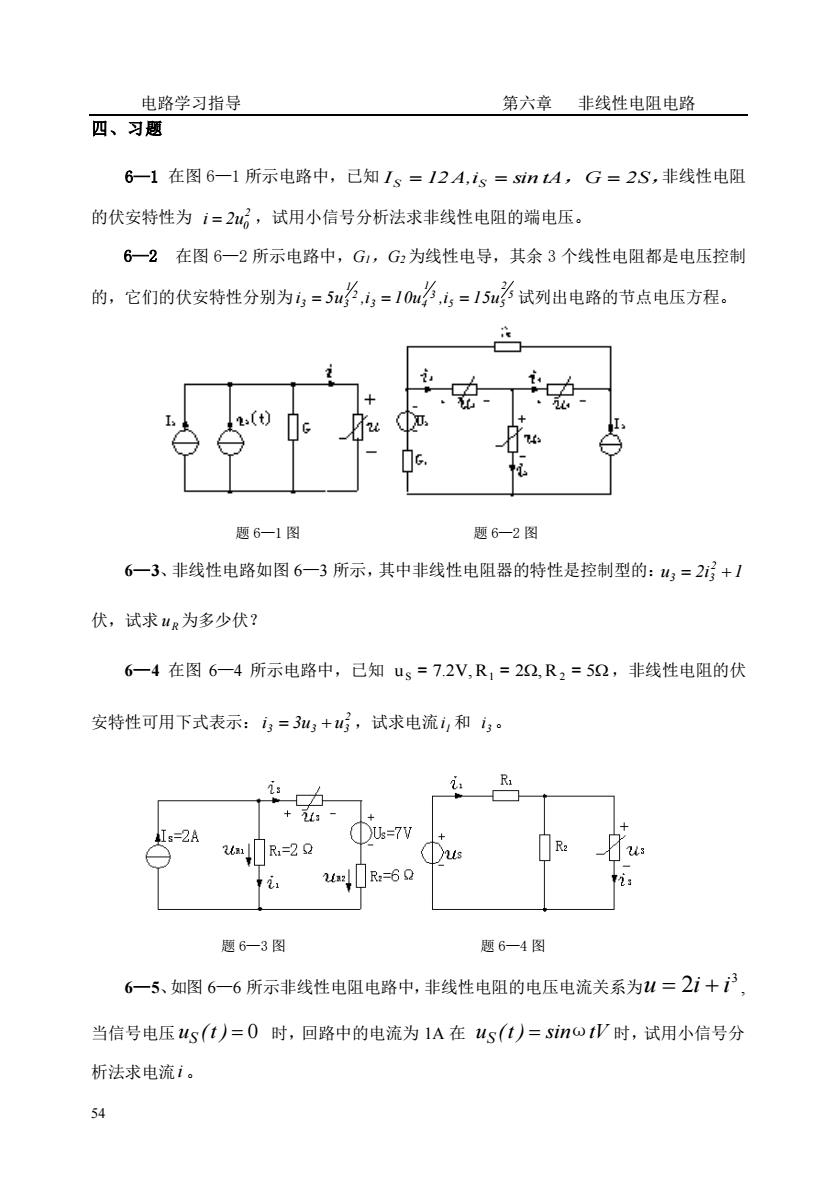
电路学习指导 第六章非线性电阻电路 四、习题 6-1在图6-1所示电路中,己知1s=12A,is=sint4,G=2S,非线性电阻 的伏安特性为1=2了,试用小信号分析法求非线性电阻的端电压。 6一2在图6一2所示电路中,G,G为线性电导,其余3个线性电阻都是电压控制 的,它们的伏安特性分别为,=5u,=10,=15u衫试列出电路的节点电压方程。 (t) 题6一1图 题6一2图 6一3、非线性电路如图6一3所示,其中非线性电阻器的特性是控制型的:4=2污+1 伏,试求山®为多少伏? 6一4在图6一4所示电路中,已知us=7.2V,R1=22,R2=52,非线性电阻的伏 安特性可用下式表示:=3+,试求电流和。 R +宏 I:=2A ①u=7v ①u R u: 题6-3图 题6-4图 6一5、如图6一6所示非线性电阻电路中,非线性电阻的电压电流关系为4=2i+户, 当信号电压us(1)=0时,回路中的电流为1A在us(t)=sinwtV时,试用小信号分 析法求电流1。 54
电路学习指导 第六章 非线性电阻电路 54 四、习题 6—1 在图 6—1 所示电路中,已知 I S = 12A,i S = sin tA,G = 2S, 非线性电阻 的伏安特性为 2 2u0 i = ,试用小信号分析法求非线性电阻的端电压。 6—2 在图 6—2 所示电路中,G1,G2 为线性电导,其余 3 个线性电阻都是电压控制 的,它们的伏安特性分别为 5 2 5 5 3 1 3 4 2 1 i 3 = 5u3 ,i = 10u ,i = 15u 试列出电路的节点电压方程。 题 6—1 图 题 6—2 图 6—3、非线性电路如图 6—3 所示,其中非线性电阻器的特性是控制型的: u 2i 1 2 3 = 3 + 伏,试求 R u 为多少伏? 6—4 在图 6—4 所示电路中,已知 u S = 7.2V,R1 = 2,R2 = 5 ,非线性电阻的伏 安特性可用下式表示: 2 3 3u3 u3 i = + ,试求电流 1 i 和 3 i 。 题 6—3 图 题 6—4 图 6—5、如图 6—6 所示非线性电阻电路中,非线性电阻的电压电流关系为 3 u = 2i + i , 当信号电压 uS (t ) = 0 时,回路中的电流为 1A 在 uS (t ) = sinωtV 时,试用小信号分 析法求电流 i

电路学习指导 第六章非线性电阻电路 66、图6一7示电路中,R=22直流电压源,U,=9p,非线性电阻的伏安特性 u=2i+写,若s)=cms1,试求电流i。 20 u=f() D 题6一5图 题6一6图 ◆6一7非线性电阻的伏安特性为“=,如此电阻突然一与个充电的电容接通,试求 电容两端的电压uc,(0)=U0。 愿6一7图 55
电路学习指导 第六章 非线性电阻电路 55 6—6、图 6—7 示电路中, R = 2 直流电压源, US = 9V ,非线性电阻的伏安特性 3 i 3 1 u = 2i + ,若 u (t ) cos t S = ,试求电流 i 。 题 6—5 图 题 6—6 图 * 6—7 非线性电阻的伏安特性为 3 u = i ,如此电阻突然一与个充电的电容接通,试求 电容两端的电压 uc,uc(0+)=U0 。 题 6—7 图