《电路》课程参考书籍（ELCTRIC CIRCUIT）CAPTER4 CIRCUIT THEOREMS

电路学习指导 第三章电阻电路的一般分析 CAPTER4 CIRCUIT THEOREMS 4-1 Linearity Property Linearity is the property of an element describing a linear relationship between cause and effect. The homogeneity property requires that if the input( excitation ) is multiplied by a constant, then the output( response )is multiplied by the same constant. The additivity property requires that the response to a sum of inputs is the sum of the responses to each input applied separately. A circuit element is a linear element if the voltage-current relationship satisfies both the homogeneity and additivity properties. In general, a circuit is linear if it is both the homogeneous and additive. A linear circuit consists only linear elements, linear dependent and independent sources. A linear circuit is one whose output is linearly related(directly proportional)to its input 4-2 Superposition If a circuit has two or more independent sources, one way to determine the value of a specific variable(voltage or current)is to use nodal or mesh analysis as in Chapte 3. Another way is to etermine the contribution of each independent source to the variable and then add them up. The later approach is known as the superposition. The superposition principle states that the voltage across(or current through) an element in a linear circuits is the algebraic sum of the voltage across(or current through) that element due to each independent source acting alone. 2. Dependent sources are left intact because they are controlled by other circuit variables. 3.Can not use superposition to determine power, because P=UI,it is not a linear variable. 4-3 Thevenin's Theorem It often occurs in practice that a particular element in a circuit is variable(load)while other elements are fixed. Each time the variable element is changed, the entire circuit has to be analyzed all over again. To avoid this problem, Thevenin's theorem provides a technique by which the fixed part of the circuit is replaced by an equivalent circuit Thevenin's theorem states that a active linear two-terminal circuit can be replaced by an equivalent circuit consisting of a voltage source Uth in series with a resister Rth.shown as Fig.4-1 Where Uth is the open-circuit voltage Uoc at the terminals(shown as Fig.4-2 a). Rth is the input or equivalent resistance Reg at the terminals when the independent sources are turned off (shown as Fig.4-2 b). To calculate Reg, we need to consider two cases: Case one: If NO has no controlled sources, Reg is the input or equivalent resistance looking between terminal a and b. Case two: If the NO has the controlled 21

电路学习指导 第三章 电阻电路的一般分析 21 CAPTER 4 CIRCUIT CIRCUIT CIRCUIT CIRCUIT THEOREMS THEOREMS THEOREMS THEOREMS 4-1 Linearity Property Linearity is the property of an element describing a linear relationship between cause and effect. The homogeneity property requires that if the input ( excitation ) is multiplied by a constant , then the output ( response ) is multiplied by the same constant . The additivity property requires that the response to a sum of inputs is the sum of the responses to each input applied separately. A circuit element is a linear element if the voltage-current relationship satisfies both the homogeneity and additivity properties. In general, a circuit is linear if it is both the homogeneous and additive . A linear circuit consists only linear elements , linear dependent and independent sources. A linear circuit is one whose output is linearly related ( directly proportional ) to its input. 4-2 Superposition If a circuit has two or more independent sources, one way to determine the value of a specific variable (voltage or current ) is to use nodal or mesh analysis as in Chapte 3. Another way is to determine the contribution of each independent source to the variable and then add them up. The later approach is known as the superposition. The superposition principle states that the voltage across (or current through) an element in a linear circuits is the algebraic sum of the voltage across (or current through) that element due to each independent source acting alone. 2. Dependent sources are left intact because they are controlled by other circuit variables. 3.Can not use superposition to determine power, because P=UI ,it is not a linear variable. 4-3 Thevenin’s Theorem It often occurs in practice that a particular element in a circuit is variable (load ) while other elements are fixed .Each time the variable element is changed , the entire circuit has to be analyzed all over again. To avoid this problem , Thevenin’s theorem provides a technique by which the fixed part of the circuit is replaced by an equivalent circuit. Thevenin’s theorem states that a active linear two-terminal circuit can be replaced by an equivalent circuit consisting of a voltage source Uth in series with a resister Rth .shown as Fig.4-1 Where Uth is the open-circuit voltage Uoc at the terminals(shown as Fig.4-2 a). Rth is the input or equivalent resistance Req at the terminals when the independent sources are turned off (shown as Fig.4-2 b).To calculate Req ,we need to consider two cases: Case one : If N0 has no controlled sources , Req is the input or equivalent resistance looking between terminal a and b. Case two:If the N0 has the controlled

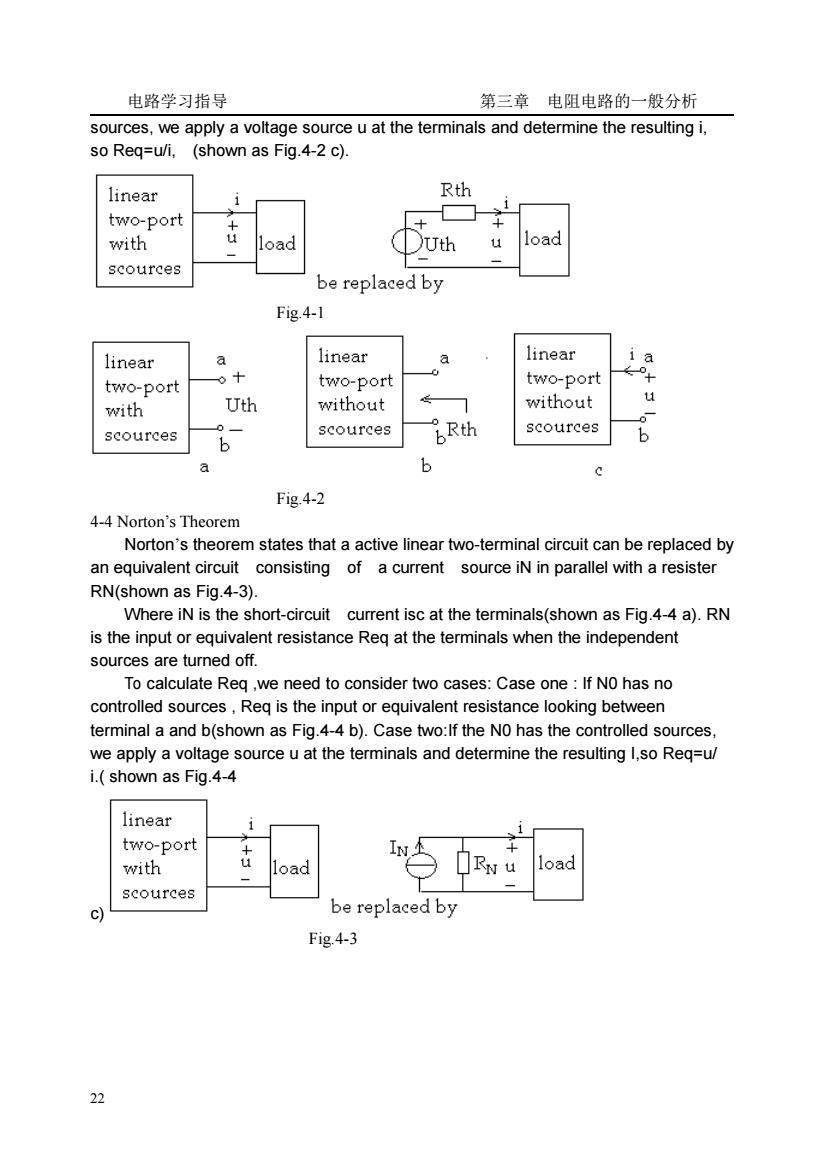
电路学习指导 第三章电阻电路的一般分析 sources,we apply a voltage source u at the terminals and determine the resulting i, so Reg=w/i.(shown as Fig.4-2 c). linear Rth two-port with )Uth scources be replaced by Fig.4-1 linear linear linear 十 two-port two-port two-port with Uth without without scources 6 scources bRth scources a b Fig.4-2 4-4 Norton's Theorem Norton's theorem states that a active linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source iN in parallel with a resister RN(shown as Fig.4-3) Where iN is the short-circuit current isc at the terminals(shown as Fig.4-4 a).RN is the input or equivalent resistance Req at the terminals when the independent sources are turned off. To calculate Reg ,we need to consider two cases:Case one:If NO has no controlled sources.Rea is the input or equivalent resistance lookina between terminal a and b(shown as Fig.4-4 b).Case two:lf the NO has the controlled sources we apply a voltage source u at the terminals and determine the resulting I,so Req=u/ i.(shown as Fig.4-4 linear two-port IN with RN scources be replaced by Fig.4-3 22

电路学习指导 第三章 电阻电路的一般分析 22 sources, we apply a voltage source u at the terminals and determine the resulting i, so Req=u/i, (shown as Fig.4-2 c). Fig.4-1 Fig.4-2 4-4 Norton’s Theorem Norton’s theorem states that a active linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source iN in parallel with a resister RN(shown as Fig.4-3). Where iN is the short-circuit current isc at the terminals(shown as Fig.4-4 a). RN is the input or equivalent resistance Req at the terminals when the independent sources are turned off. To calculate Req ,we need to consider two cases: Case one : If N0 has no controlled sources , Req is the input or equivalent resistance looking between terminal a and b(shown as Fig.4-4 b). Case two:If the N0 has the controlled sources, we apply a voltage source u at the terminals and determine the resulting I,so Req=u/ i.( shown as Fig.4-4 c) Fig.4-3

电路学习指导 第三章电阻电路的一般分析 linear linear linear two-port two-port two-por with without without scources scources RN scources b Fig.4-4 4-4 Maximum Power Transfer In many practical situations.a circuit is designed to provide power to a load.How does the load can draw the maximum power from the given source We assume that we can adjus the load resistance RL.If the entire circuit is replaced by its Thevenin equivalent except for the load.shown as Fig.4-5 Rth Uth R Fig.4-5 In many practical situations.a circuit is designed to provide power to a load.How does the load can draw the maximum power from the given source.We can prove that the maximum power is transferred to the load when the load resistance equals to the Thevenin resistance as seen from the load.That is when RL=Rth,the maximum power is: P= U 4Rth 4-6 Examples E4-1 Assume Io=1A and use linearity to find the actual value of the circuit in Fig E4-1 U222Q u 30 Is=15A 3 72 40 50 Fig.E4-1 Solution: If Io=1A,then Ul=(3+5)Io=8V and I1=U1/4=2A. Applying KCLat node lgives -1+3A S0U2=U1+2I2=8+6=14V,I3=U2/7=2A 23

电路学习指导 第三章 电阻电路的一般分析 23 Fig.4-4 4-4 Maximum Power Transfer In many practical situations, a circuit is designed to provide power to a load. How does the load can draw the maximum power from the given source. We assume that we can adjust the load resistance RL . If the entire circuit is replaced by its Thevenin equivalent except for the load, shown as Fig.4-5 Fig.4-5 In many practical situations, a circuit is designed to provide power to a load. How does the load can draw the maximum power from the given source. We can prove that the maximum power is transferred to the load when the load resistance equals to the Thevenin resistance as seen from the load. That is when RL=Rth, the maximum power is: Rth U P th 4 2 = 4-6 Examples E4-1 Assume Io=1A and use linearity to find the actual value of the circuit in Fig.E4-1. Fig.E4-1 Solution: If Io=1A, then U1=(3+5)Io=8V and I1=U1/4=2A. Applying KCL at node 1 gives I2=I1+Io=3A So U2=U1+2I2=8+6=14V ,I3=U2/7=2A

电路学习指导 第三章电阻电路的一般分析 Applying KCL to node 2 gives Is=13+12=5A Therefore,Is=5A.This shows that assuming Io=1 gives Is=5A;the actual source current of 15A will give Io=3A as the actual value.(homogeneous property) E4-2 Use superposition to calculate U and I in Fig.E4-2a. Solution A When 3A current source acts alone,the 9V voltage source is turned off (shown as Fig.E4-2 b),thus U0=5=5×2=10V B When the 9v voltage source acts alone 3A current source is turned off (shown as Fig.E4-2 c),thus 12= 9 =-0.6A;U2'=512=5×(-0.6)=-3V 10+5 15 159 15 20Q 200 20 9 9 100 10 (b) c Fig.E4-2 C When both the 9V voltage source and the 3A current source act U=U04U2'=10+(-3)=7V 1+2=2+ (-0.6)=14A E4-3 The circuit is shown as Fig.E4-3,determine U3. 10I 06Q 10 6 10u 4 3D10 4 4 (a) (b) FigE4-3图4-2 例4一2图 24

电路学习指导 第三章 电阻电路的一般分析 24 Applying KCL to node 2 gives Is=I3+I2=5A Therefore , Is=5A. This shows that assuming Io=1 gives Is=5A; the actual source current of 15A will give Io=3A as the actual value. (homogeneous property) E4-2 Use superposition to calculate U and I in Fig.E4-2a. Solution: A When 3A current source acts alone , the 9V voltage source is turned off (shown as Fig.E4-2 b) , thus I（1）= 10 5 10 + ×3=2A ; U(1)=5I (1)=5×2=10V B When the 9V voltage source acts alone , 3A current source is turned off (shown as Fig.E4-2 c) , thus I（2）=－ 10 5 9 + =－0.6 A ; U（2）=5I（2）=5×（－0.6）= －3V Fig.E4-2 C When both the 9V voltage source and the 3A current source act U=U(1)+U（2）=10+（－3）=7V I=I（1）+I（2）=2+（－0.6）=1.4A E4-3 The circuit is shown as Fig.E4-3 , determine U3. Fig.E4-3 图 4—2 例 4—2 图

电路学习指导 第三章电阻电路的一般分析 A When the 10V voltage source acts alone,4A current source is replaced by open circuit (shown as Fig.E4-3 b),thus 1甲=P=9A U9=-1010+4I9=(-10+4)×1=-6V A When the 4A current source acts alone,10V voltage source is replaced by short circuit (shown as Fig.E4-3c),thus =- 4+6X4-1.6A 4 I2=4+I2)=4+(-1.6)=2.4A U2=-1012+412=-10×(-1.6)+4×2.4=25.6V S0U3=U9+U2=-6+25.6=19.6V E4-4 The circuit is shown as Fig.E4-4.No is a network without independent sources.When Us=4V,Is=2A,Ux=8V;when Us=7V,Is=1A,Ux=6V.When Us=2V,Ix=6A,Ux=? Solution: According superposition 0+U0 Ux=k Us+kols When Us=4V,Is=2A,Ux=8V. That is 8V=kiX4+k2X2=4kr+2k When Us=7V,Is=1A,Ux=6V, That is 6=7k+1k2 S0k1=0.4,k2=3.2Q Ux=0.4Us+3.22X1s Fig.E4-4 Thus,when Us=-2V,x=6A,Ux=0.4×2+3.2×6=20V E4-5 Determine the Thevenin equivalent circuit of the circuit shown as Fig.E4-5. 9V 1002 3 6V Uoc 62 162 102 102 b (a) (b) (c)

电路学习指导 第三章 电阻电路的一般分析 25 A When the 10V voltage source acts alone , 4A current source is replaced by open circuit (shown as Fig.E4-3 b) , thus I（1） 1 = I（2） 1 = 6 4 10 + =1A U（1） 3 =－10 I（1） 1 +4 I（1） 2 =（－10+4）×1=－6V A When the 4A current source acts alone , 10V voltage source is replaced by short circuit (shown as Fig.E4-3 c) , thus I（2） 1 =－ 4 6 4 + =×4= －1.6A I（2） 1 = 4+ I（2） 1 = 4+（－1.6）=2.4A U（2） 3 = －10 I（2） 1 +4 I（2） 1 = －10×（－1.6）+4×2.4=25.6V So U 3 = U（1） 3 + U（2） 3 =－6+25.6=19.6V E4-4 The circuit is shown as Fig.E4-4, No is a network without independent sources . When Us=4V, Is=2A,，Ux=8V; when Us=7V，Is=1A,，Ux=6V. When Us=2V，Ix=6A,Ux=? Solution: According superposition Ux=k1Us+k2Is When Us=4V，Is=2A，Ux=8V, That is 8V=k1×4+k2×2=4k1+2k2 When Us=7V，Is=1A，Ux=6V， That is 6=7k1+1k2 So k1=0.4 , k 2=3.2Ω Ux=0.4Us+3.2Ω×Is Fig.E4-4 Thus , when Us=2V，Ix=6A， Ux= 0.4×2+3.2×6=20V E4-5 Determine the Thevenin equivalent circuit of the circuit shown as Fig.E4-5. (a) (b) (c) U U X

电路学习指导 第三章电阻电路的一般分析 Fig.E4-5 Solution: First,calculate Uoc Because the at terminal a and b,the circuit is opened,I=I2=2A U0c=-6+6×2-6V Second,calculate the Req,we should turn the original circuit into a circuit without source that means we should use the short circuit to replace the voltage source and use the open circuit to replace thecurrent source(shown as Fig E4-5 b) Thus Req=10+6=16 and the equivalent circuit is shown as Fig.E4-5 c. E4-6 Determine the current flowing through the 6ohms resistor in the circuit shown as Fig.E4 Is 20 10A 69 40 R62 52 (b) 6 FigE4-6 Solution: First,we should get a one port by open the 6 ohms resistor,that is open the branch ab shown as Fig.E4-6 a.And calculate the open circuit voltage Us=Uoc=Uab=4Is-10=4X10-10=30V Next,we set all the independent sources into zeros,and find the equivalent resistanc Req loking from port ab shown as Fig.E4-6 b,thus Req=Rab=R=4 Now,we get the equivalent circuit shown as the left part of Fig.E4-6.c,then connect the 6 ohms to terminal a and b. Us 30 l:Req+R:4+6 3A 26

电路学习指导 第三章 电阻电路的一般分析 26 Fig.E4-5 Solution: First , calculate Uoc Because the at terminal a and b , the circuit is opened , 1I = 2 I =2A Uoc= －6+6×2=6V Second , calculate the Req ， we should turn the original circuit into a circuit without source,that means we should use the short circuit to replace the voltage source and use the open circuit to replace thecurrent source (shown as Fig.E4-5 b) Thus Req=10+6=16Ω and the equivalent circuit is shown as Fig.E4-5 c. E4-6 Determine the current flowing through the 6 ohms resistor in the circuit shown as Fig.E4-6 a using Thevenin theorem. Fig.E4-6 Solution: First , we should get a one port by open the 6 ohms resistor , that is open the branch ab shown as Fig.E4-6 a.And calculate the open circuit voltage Us=Uoc=Uab= 4Is－10 = 4×10－10=30V Next , we set all the independent sources into zeros , and find the equivalent resistanc Req loking from port ab shown as Fig.E4-6 b, thus Req=Rab= R4 =4Ω Now , we get the equivalent circuit shown as the left part of Fig.E4-6.c, then connect the 6 ohms to terminal a and b. So, I2= 4 6 30 Re q R Us 2 + = + =3A 10A (a) + 10V - b 4Ω 5Ω (b) 5Ω b 4Ω I2 6Ω IS 2Ω R2 a 2Ω a US R2 (c) Req - b 6Ω + a I2

电路学习指导 第三章电阻电路的一般分析 E4-7 Determine the Thevenin and Norton equivalent circuit of the circuit shown as Fig.E4-7 -5K9 35v 02.5x0 b b (a) 6) a ○h4A2.5xg (c) 6八 (d) Where ic=0.75i Fig.E4-7 Solution A When port ab is open-circuited(Fig.E5-7a) i2=i,+ic=i1+0.75i1=1.75i1 at mesh1,the KVLis5×103×i1+20×103i2=40 because ic=1.75i,then we get i=10mA, and Uoc=20×103×i2=35V,as show in Fig.E5-7b B When port ab is short-circuited (Fig.E5-7c)we can get is. 40 i0x10-8A so,isc=i+i=i,+0.75i,=1.75i,=1.75×8=14mA;(Fig.E5-7d CThe equivalent resistor Rin-Req-Uoc-35 114x102.5k0

电路学习指导 第三章 电阻电路的一般分析 27 E4-7 Determine the Thevenin and Norton equivalent circuit of the circuit shown as Fig.E4-7 Where i C ＝0.75i. Fig.E4-7 Solution: A When port ab is open-circuited (Fig.E5-7a) i 2 = i +i c =i1 +0.75i1=1.75i1 at mesh 1 , the KVL is 5×10 3×i1 +20×10 3 i 2 =40 because ic=1.75i1 ，then we get i =10mA， and Uoc= 20×103×i2= 35V ，as show in Fig.E5-7b B When port ab is short-circuited (Fig.E5-7c) we can get i sc . i = 3 50 × 10 40 =8mA So , i sc =i1+iC= i1+0.75i1=1.75i1 =1.75×8=14mA; (Fig.E5-7d) C The equivalent resistor Rin=Req= sc I Uoc = 3 14 10 35 × =2.5kΩ (c) b 2 2 20KΩ 20KΩ - 40V 1 - + I 5KΩ (a) 1 40V + 5KΩ I a sc b - a + (d) b 2.5KΩ 14mA 2.5KΩ (b) b a 35V - + a

电路学习指导 第三章电阻电路的一般分析 E4-8 The circuit is shown as Fig.E4-8,find the R when it can get the maximum power,and determine the maximum power of RL PLmux 210 50a i10 10 11w 5.180 .180 5 6 (6) (c)b Fig.E4-8 Solution: First,open the load,and connect a voltage uat terminal a and b(shown as Fig E4-8b).then we find the relationship of u and I by using KVL,so we get U=1+20+4i+i)=7I+101 :i=11-(U-50-11-1Sx*5I 10 U=5.18+10 By compare the coefficients of the VCR of Thevenin's equivalent circuit U=Us-RI,we can straightly get the voltage is 10V,the resistance is 5.18Q.hen we get the equivalent circuit shown as Fig.E4-8c. So R=Req=5.182 And U 102 PLm44x3i8438w E4-9The circuit is shown as Fig.E4-9a,determine current I using reciprocal theorem 20 4 4 Fig.E4-9 Solution: According to the reciprocal theorem,8V acts in branch ab will result the current I in branch cd. 28

电路学习指导 第三章 电阻电路的一般分析 28 E4-8 The circuit is shown as Fig.E4-8 , find the RL when it can get the maximum power , and determine the maximum power of RL PLmax Fig.E4-8 Solution : First , open the load , and connect a voltage u at terminal a and b (shown as Fig.E4-8b ), then we find the relationship of u and I by using KVL, so we get U=5I+2(I+4i+i)=7I+10i ∵i= Ω − − 1 11 （U 5I） =11－1S×U+5I U=5.18I+10 By compare the coefficients of the VCR of Thevenin’s equivalent circuit U=Us－RI, we can straightly get the voltage is 10V，the resistance is 5.18Ω. hen we get the equivalent circuit shown as Fig.E4-8 c. So RL=Req=5.18Ω And P L max = 4.38w 4 5.18 10 4Rs U2 2 S = × = ; E4-9 The circuit is shown as Fig.E4-9a , determine current I using reciprocal theorem. Fig.E4-9 Solution : According to the reciprocal theorem , 8V acts in branch ab will result the current I in branch cd

电路学习指导 第三章电阻电路的一般分析 and 8V acts in branch cd will result the current I in branch ab shown as Fig.E4-9b. In Fig.E4-9b.I1=- 8 8 2+ 4x21×2= 4+21+2 *4 By using current division,we can obtain 1 B2= 6=421=x2-A 4 treCl -t号号A 0ngE4卡号A E4-10 The circuit is shown as Fig E4-10a,the load is 5 ohms,find the I flowing through the resistor. b Fig E4-10 Solution In Fig E4-10a, / 6+3=11.50%=-61+31=-3/=-3 e他em绍-型=6号+3号-2以 3 3 Thus B= The Thevenin equivalent circuit is shown as Fig E4-10c,because I=-1A,the 5 ohms resistor

电路学习指导 第三章 电阻电路的一般分析 29 and 8V acts in branch cd will result the current I in branch ab shown as Fig.E4-9b. In Fig.E4-9b. I1= 2A 3 2 3 4 2 8 1 2 1 2 4 2 4 2 2 8 = + + = + × + + × + By using current division , we can obtain I2 = A 3 2 2 3 1 I 1 2 1 × 1 = × = + I3 = A 3 4 2 3 1 I 41 2 4 × 1 = × = + Using KCL，I= I3－I2= A 3 2 3 2 3 4 − = So in Fig.E4-9a I= A 3 2 E4-10 The circuit is shown as Fig E4-10a , the load is 5 ohms , find the I flowing through the resistor. 9 V I 6 Ω 3 Ω 6 I U o I 6 Ω 3 Ω 6 I U I 1 5 Ω - 2 Ω - 3 V I a b c Fig E4-10 Solution: In Fig.E4-10a, 9 1 6 3 I A = = + , So 6 3 3 3 U I I I V O = − + = − = − Using Fig.E4-10b, we get 1 6 1 2 3 6 3 I I I = = + and 1 1 1 2 2 6 3 2 3 3 I I U I = − × + × = − Thus 1 2 i U R I = = − Ω The Thevenin equivalent circuit is shown as Fig.E4-10c , because I=-1A, the 5 ohms resistor

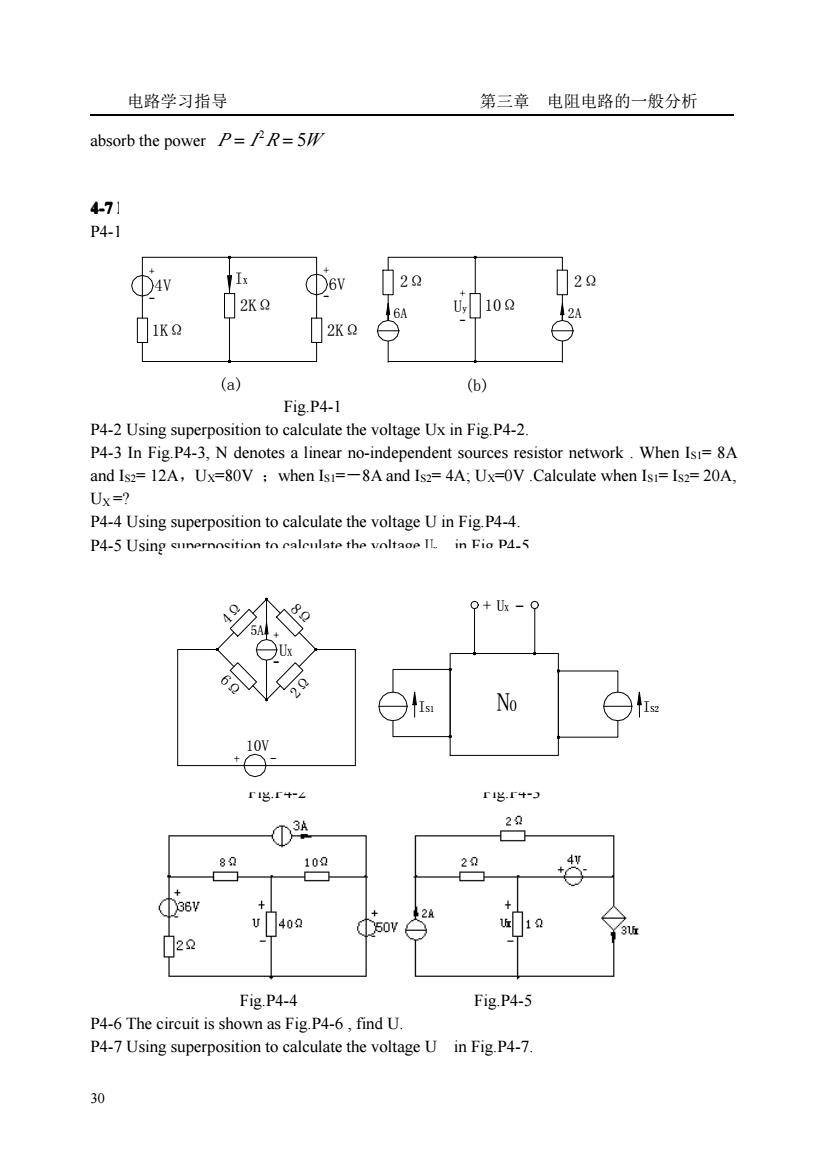
电路学习指导 第三章电阻电路的一般分析 absorb the power P=/R=5/ 4-7 P4-1 ①4W 2K ,102 1KQ (a) (6) Fig.P4-1 P4-2 Using superposition to calculate the voltage Ux in Fig.P4-2. P4-3 In Fig.P4-3 N denotes a linear no-independent sources resistor network.When Is=8A and Is2=12A,Ux=80V when Is1=-8A and Is2=4A;Ux=0V .Calculate when Isi=Is2=20A, Uy=? P4-4 Using superposition to calculate the voltage U in Fig P4-4. P4-5 Using sunernocition to caleulate the voltaoe IL in Fio P4.5 9+U-o 60 10 36y 400 722 Fig.P4-4 Fig.P4-5 P4-6 The circuit is shown as Fig.P4-6,find U. P4-7 Using superposition to calculate the voltage U in Fig.P4-7 30

电路学习指导 第三章 电阻电路的一般分析 30 absorb the power 2 P I R W = = 5 4-7 Problems Problems Problems Problems P4-1 Using superposition to calculate IX Uy in Fig.P4-1a and Fig.P4-1b. Fig.P4-1 P4-2 Using superposition to calculate the voltage Ux in Fig.P4-2. P4-3 In Fig.P4-3, N denotes a linear no-independent sources resistor network . When IS1= 8A and IS2= 12A，UX=80V ；when IS1=－8A and IS2= 4A; UX=0V .Calculate when IS1= IS2= 20A, UX =? P4-4 Using superposition to calculate the voltage U in Fig.P4-4. P4-5 Using superposition to calculate the voltage UX in Fig.P4-5. Fig.P4-2 Fig.P4-3 Fig.P4-4 Fig.P4-5 P4-6 The circuit is shown as Fig.P4-6 , find U. P4-7 Using superposition to calculate the voltage U in Fig.P4-7. 4V 6V 2Ω 2Ω (b) 2KΩ Uy (a) 1KΩ - 2KΩ - 6A + - 2A 10Ω + IX + + - 10V 6Ω 4Ω 5A UX 2Ω - IS1 8Ω + N0 IS2 + UX -