
自动控制理论 第四章根轨迹法 新腰大学电气工程学院
第四章根轨迹法 新疆大学 电气工程学院 自动控制理论
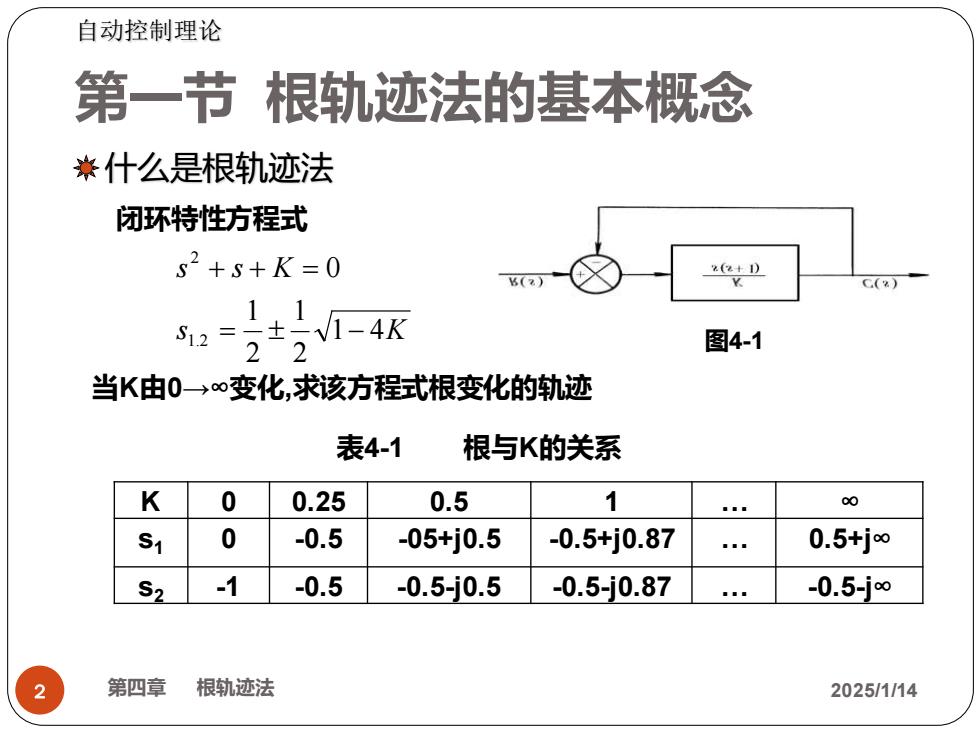
自动控制理论 第一节根轨迹法的基本概念 米什么是根轨迹法 闭环特性方程式 s2+S+K=0 (2+) () C(%) S2=+1-4K 22 图4-1 当K由0→∞变化,求该方程式根变化的轨迹 表4-1 根与K的关系 K 0 0.25 0.5 1 oo S1 0 -0.5 -05+j0.5 -0.5+j0.87 0.5+j∞ S2 -1 -0.5 -0.5j0.5 -0.5-j0.87 -0.5-j∞ 第四章 根轨迹法 2025/1/14
第一节 根轨迹法的基本概念 2 第四章 根轨迹法 2025/1/14 s K s s K 1 4 2 1 2 1 0 1.2 2 = − + + = K 0 0.25 0.5 1 . ∞ s1 0 -0.5 -05+j0.5 -0.5+j0.87 . 0.5+j∞ s2 -1 -0.5 -0.5-j0.5 -0.5-j0.87 . -0.5-j∞ 自动控制理论 什么是根轨迹法 图4-1 闭环特性方程式 当K由0→∞变化,求该方程式根变化的轨迹 表4-1 根与K的关系

自动控制理论 对于不同的K值,系统有下列三种不同的工作状态 1)0≤K如要求系统在阶跃信号的作用下,超调量为49。 jol 求一对希望的闭环极点,由式(3-26)求得 =0.707,=arctan0.707=45°在图4-2上过 -K=0.5 坐标原点作与负实轴夹角为45°和射线,它与 =0.25 K=0 根轨迹的交点S=-05±j0.5这就是所求的希望 -0.5 闭环极点。 K=0.5 图4-2 第四章 根轨迹法 2025/1/14
3 第四章 根轨迹法 2025/1/14 图4-2 对于不同的K值,系统有下列 三种不同的工作状态 1) 0≤K<¼, s1、 s1为两相异的实数根(过阻尼状态) 2) K=¼, s1 = s2 =-0.5,(临界阻尼) 3) ¼<K<∞ , s1 、s2为一对共轭复根(欠阻尼) ➢如要求系统在阶跃信号的作用下,超调量为49。 求一对希望的闭环极点,由式(3-26)求得 ξ=0.707,β=arctan0.707=45°在图4-2上过 坐标原点作与负实轴夹角为45°和射线,它与 根轨迹的交点S= -05±j0.5这就是所求的希望 闭环极点。 自动控制理论
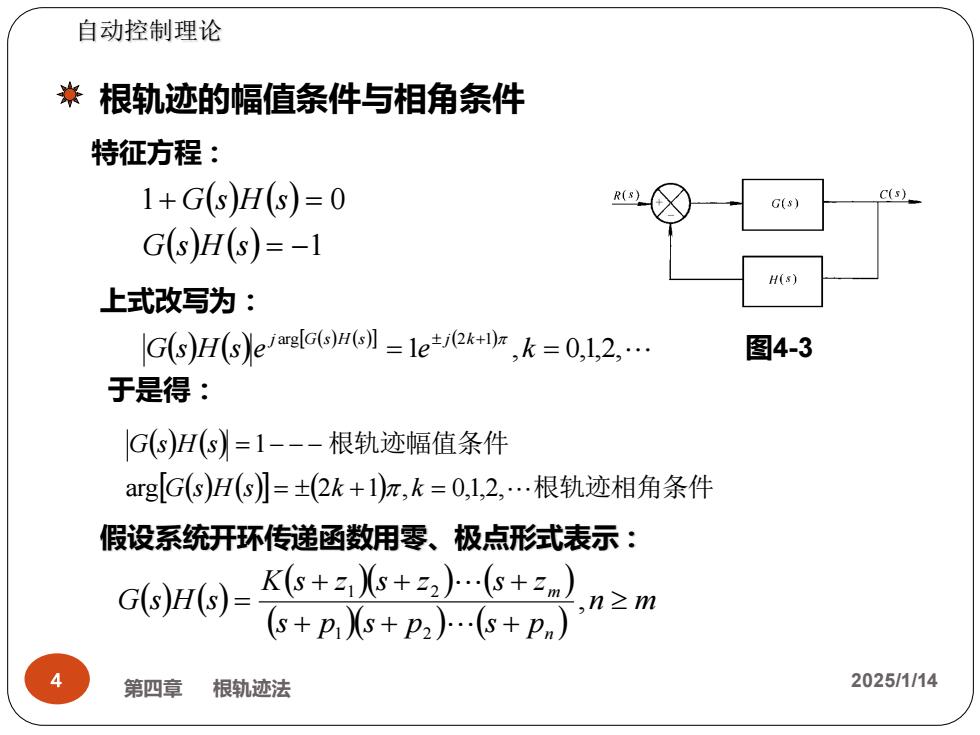
自动控制理论 根轨迹的幅值条件与相角条件 特征方程: 1+G(s)H(s)=0 R( C(s) G() G(s)H(s)=-1 H(s) 上式改写为: G(S)H(s)e=1e-ktI,k=0.12. 图4-3 于是得: G(s)H(s=1-根轨迹幅值条件 arg[Gs)H(s】=±(2k+1)π,k=0,l,2,.根轨迹相角条件 假设系统开环传递函数用零、极点形式表示: G6)H)=K6++)-s+2 ,n≥m (s+Pi)s+p2).(s+p) 第四章 根轨迹法 2025/1/14
( ) ( ) ( ) ( ) 1 1 0 = − + = G s H s G s H s ( ) ( ) ( ) ( ) ( ) 根轨迹相角条件 根轨迹幅值条件 arg 2 1 , 0,1,2, 1 = + = = − − − G s H s k k G s H s 4 第四章 根轨迹法 2025/1/14 图4-3 根轨迹的幅值条件与相角条件 特征方程: 上式改写为: 自动控制理论 ( ) ( ) G s H s e j argG(s)H(s) =1e j(2k+1) ,k = 0,1,2, 于是得: 假设系统开环传递函数用零、极点形式表示: ( ) ( ) ( )( ) ( ) ( )( ) ( ) n m s p s p s p K s z s z s z G s H s n m + + + + + + = , 1 2 1 2
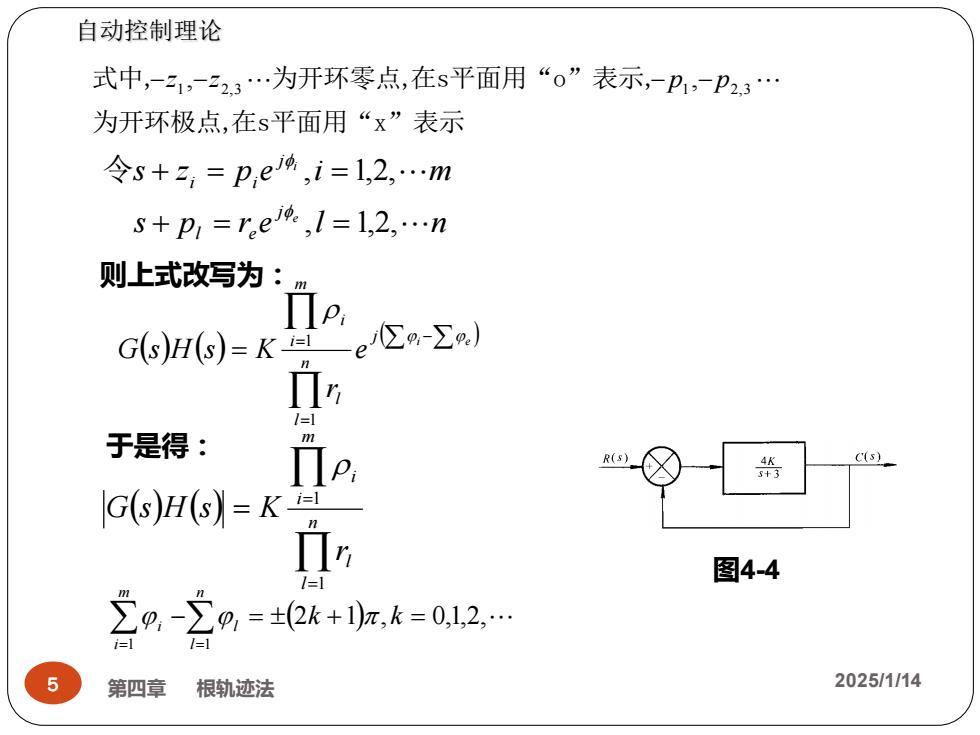
自动控制理论 式中,-,-23.为开环零点,在s平面用“0”表示,-P,一P23. 为开环极点,在s平面用“x”表示 令s+z,=p,e9,i=1,2.m S+p,=e9,1=1,2,.n 则上式改写为: G(s)H(s)=K—e E-∑) i 于是得: m R(s) C(s) G)H(s=K 1 图4-4 20,-立0=±0k+z,k=012 5 第四章 根轨迹法 2025/1/14
( ) ( ) ( ) = − = = i e j n l l m i i e r G s H s K 1 1 5 第四章 根轨迹法 2025/1/14 自动控制理论 为开环极点,在s平面用“x”表示 式中,−z1 ,−z2,3为开环零点,在s平面用“o”表示,− p1 ,− p2,3 s p r e l n s z p e i m e i j l e j i i , 1,2, , 1,2, + = = + = = 令 则上式改写为: 图4-4 于是得: (2 1) , 0,1,2, 1 1 − = + = = = k k n l l m i i ( ) ( ) = = = n l l m i i r G s H s K 1 1

自动控制理论 结论: >幅值条件与K有关,相角条件与K无关 K=1.5 >满足相角条件的点必然满足幅值条件。 K=1 K-0.5 反之,满足幅值条件点未必能满足相角条件 幅值条件: 41 1 s+3 K 令s=o+jo代入上式,得 (o+3)2+o2=(4K)2 图4-5 >系统的等增益轨迹是一簇同心圆,对于某一个确定的K值,对应圆 周上有无穷多个S值都满足方程,其中只有同时满足相角条件的$值 才是方程的根。 >根轨迹就是S平面上满足相角条件点的集合。 6 第四章 根轨迹法 2025/1/14
( ) ( ) 2 2 2 3 4 1 3 4 K s j s K + + = = + = + 令 代入上式,得 6 第四章 根轨迹法 2025/1/14 ➢幅值条件与K有关,相角条件与K无关 ➢满足相角条件的点必然满足幅值条件。 反之,满足幅值条件点未必能满足相角条件。 自动控制理论 结论: 图4-5 幅值条件: ➢系统的等增益轨迹是一簇同心圆,对于某一个确定的K值,对应圆 周上有无穷多个S值都满足方程,其中只有同时满足相角条件的S值 才是方程的根。 ➢根轨迹就是S平面上满足相角条件点的集合

自动控制理论 >绘制根轨迹步骤 1)先找出S平面上满足相角条件的点,并把它们连成曲线: 2)用幅值条件确定相应点对应的K值。 例4-1求图4-1所示系统的根轨迹 解:1)用相角条件绘制根轨迹 G(s)= K s(+1) -ags+arg6s+1刃=±2k+1z,k=01,2, 2)用幅值条件确定增益K K=s s+1 例如s2=0.5,K=-0.50.5=0.25 第四章 根轨迹法 2025/1/14
−arg s + arg(s +1) = (2k +1),k = 0,1,2, 第四章 根轨迹法 2025/1/14 7 ➢绘制根轨迹步骤 1)先找出S平面上满足相角条件的点,并把它们连成曲线; 2)用幅值条件确定相应点对应的K值。 例4-1 求图4-1所示系统的根轨迹 解: 1)用相角条件绘制根轨迹 自动控制理论 ( ) (+1) = s K G s 2)用幅值条件确定增益K K = s s +1 例如s1,2 = −0.5,K = − 0.5 0.5 = 0.25
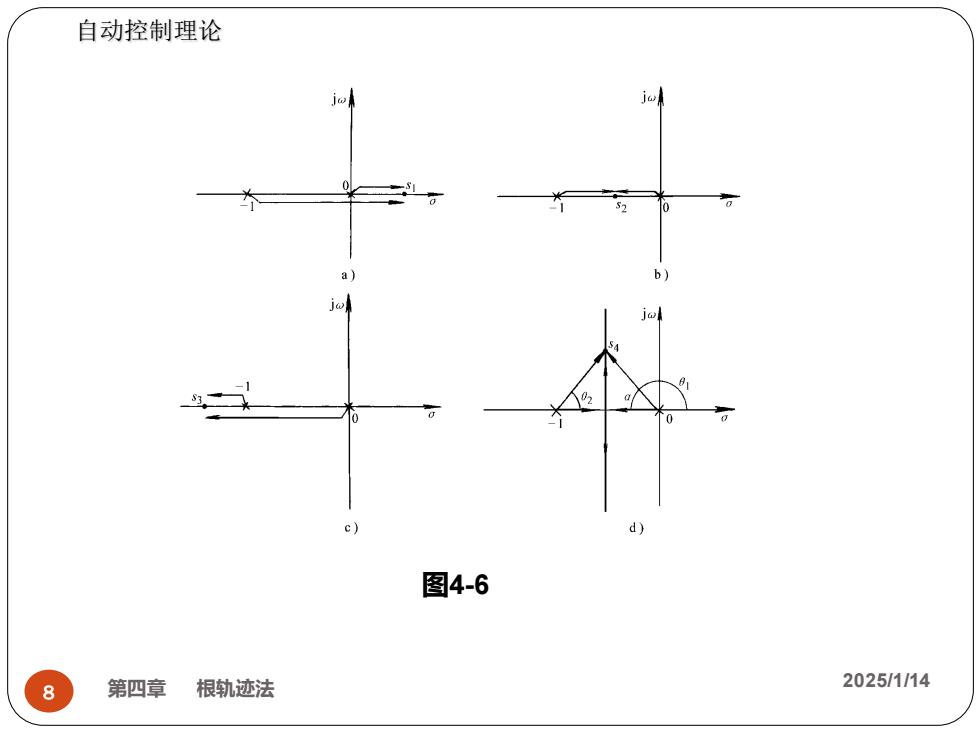
自动控制理论 d) 图4-6 8 第四章 根勃迹法 2025/1/14
第四章 根轨迹法 2025/1/14 8 图4-6 自动控制理论

自动控制理论 第二节根轨迹的基本规则 开环传递函数有如下两种表示: K(,s+1) G(s)H(s= n≥m (4-12) s+) 1=1 或 K6+z) G(s)H(s)= n≥m(4-13) T6+p,) 其中,K为系统的开环增益;K为系统的根轨迹增益它们之间的 关系为: 9 第四章 根轨迹法 2025/1/14
第二节 根轨迹的基本规则 9 第四章 根轨迹法 2025/1/14 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , (4 -13) , 4 -12 1 1 1 1 0 1 1 n m s p K s z G s H s n m T s K s G s H s n l l m i i n l l m i i + + = + + = = = = = 或 开环传递函数有如下两种表示: 自动控制理论 其中,K为系统的开环增益;K0为系统的根轨迹增益它们之间的 关系为:

自动控制理论 K ,n≥m (4-14) 1=1 来绘制根轨迹的基本规则 规则1:根轨迹的对称性 由于系统特征方程式的系数均为实数,因而特征根或为实数,或为 共轭复数.根轨迹必然对称于S平面的实轴 规则2:根轨迹的分支数及其起点和终点 闭环特征方程: (s+p)+KT(s+2,)=0 >当k由0→o变化时,方程中任一根由始点连续地向终点变化的轨迹称 为根轨迹的一条分支; 10 第四章 根轨迹法 2025/1/14
10 第四章 根轨迹法 2025/1/14 , (4 -14) 1 1 0 n m p K z K n l l m i i = = = 绘制根轨迹的基本规则 规则1:根轨迹的对称性 由于系统特征方程式的系数均为实数,因而特征根或为实数,或为 共轭复数.根轨迹必然对称于S平面的实轴 规则2:根轨迹的分支数及其起点和终点 闭环特征方程: ( ) ( ) 0 1 0 1 + + + = = = m i i n l l s p K s z 自动控制理论 ➢当k由 0 → 变化时,方程中任一根由始点连续地向终点变化的轨迹称 为根轨迹的一条分支;