
现代控制理论实验 第二部分现代控制理论 实验一用MATLAB进行数学模型的变换 一、实验目的 1.学习MATLAB语言中常用命令 2.利用MATLAB编程完成数学模型的变换: 3.进一步加深对所学理论的理解: 二、主要实验设备及仪器 1.计算机一台 2.MATLAB软件 三、实验内容 系统的闭环传递函数为: 相应的状态空间表达式为: Y(s)num(s) 文=Ax+Bu U(s)den(s) y=Cx+Du 1.由系统的闭环传递函数转换为状态空间表达式: 函数格式为: [A B C D]=tf2ss(num,den) 例如 Y(s)」 S2+25+3 U(s)s3+5s2+7s+6 程序为: num=[123: de=[1576: [A BC D]=tf2ss(num,den) 运行结果为: A=5-7 -6B=1 C=1 2 3 D=0 0 0 0 0 1 0 0 「-5-7-61「1 =100x+04 即: 010」0o y=l23 若加入g=s(A,B,C,D),则继续显示:
现代控制理论实验 39 第二部分 现代控制理论 实验一 用 MATLAB 进行数学模型的变换 一、实验目的 1.学习 MATLAB 语言中常用命令; 2.利用 MATLAB 编程完成数学模型的变换; 3.进一步加深对所学理论的理解; 二、主要实验设备及仪器 1.计算机一台 2.MATLAB 软件 三、实验内容 系统的闭环传递函数为: 相应的状态空间表达式为: ( ) ( ) ( ) ( ) den s num s U s Y s = y Cx Du x Ax Bu = + = + 1.由系统的闭环传递函数转换为状态空间表达式: 函数格式为: [A B C D]=tf2ss(num,den) 例如: 5 7 6 2 3 ( ) ( ) 3 2 2 + + + + + = s s s s s U s Y s 程序为: num=[1 2 3]; den=[1 5 7 6]; [A B C D]=tf2ss(num,den) 运行结果为: 即: y x x x u 1 2 3 0 0 1 0 1 0 1 0 0 5 7 6 = + − − − = 若加入 g=ss(A,B,C,D),则继续显示: A = -5 -7 -6 1 0 0 0 1 0 B = 1 0 0 C = 1 2 3 D = 0

现代控制理论实验 as b= c= d= xl x2 x3 ul xl x2 x3 ul 5 -7-6 x11 y1123 y10 0 0 x2 0 Continuous-time x3010 X30 model. 2.由系统的状态空间表达式转换为闭环传递函数: (1)单输入一单输出系统: 函数格式为:Inum,den=ss2tf(a,b,c,d) 01-1]「0 例如: x=-6-116x+04 -6-1151 y=100x 程序为:a=01-1,-6-116,-6-115小 b=001]: c=100: d-[01 [num,den]=ss2tf(a.b.c.d) 运行结果为: num= 0 0.0000 -1.0000 -5.0000 den=1.0000 6.0000 11.0000 6.0000 即:W(s)= 8-5 c3+62+118+6 (2)多输入一多输出系统: 函数格式为: NUM,den=ss2tf(a.b.c.d,iu) iu表示第几个输入,例如=2,则iu分别为1、2 「1241 「301 x=345x+60u 例如: 14221 「1421「00] y=462r+i0 程序为: a=124:345:142 b-362:001] c=142:462: d-00,10: %
现代控制理论实验 40 2.由系统的状态空间表达式转换为闭环传递函数: (1) 单输入—单输出系统: 函数格式为:[num,den]=ss2tf(a,b,c,d) 例如: y x x x u 1 0 0 1 0 0 6 11 5 6 11 6 0 1 1 = + − − − − − = 程序为: a=[0 1 -1;-6 -11 6;-6 -11 5]; b=[0 0 1]'; c=[1 0 0]; d=[0]; [num,den]=ss2tf(a,b,c,d) 运行结果为: num = 0 0.0000 -1.0000 -5.0000 den = 1.0000 6.0000 11.0000 6.0000 即: 6 11 6 5 ( ) 3 2 + + + − − = s s s s W s (2)多输入—多输出系统: 函数格式为: [NUM,den]=ss2tf(a,b,c,d,iu) iu 表示第几个输入,例如 r=2,则 iu 分别为 1、2 例如: y x u x x u + = + = 1 0 0 0 4 6 2 1 4 2 2 1 6 0 3 0 1 4 2 3 4 5 1 2 4 程序为: a=[1 2 4;3 4 5;1 4 2]; b=[3 6 2;0 0 1]'; c=[1 4 2;4 6 2]; d=[0 0;1 0]; a = x1 x2 x3 x1 -5 -7 -6 x2 1 0 0 x3 0 1 0 b = u1 x1 1 x2 0 x3 0 c = x1 x2 x3 y1 1 2 3 d = u1 y1 0 Continuous-time model

现代控制理论实验 [NUM,den]=ss2tf(a,b,c,d,1) INUM den =ss2tf(a.b.c.d.2) 运行结果为: NUM=0 310000 40.0000 36.0000 1.0000 45.0000 32.0000 88.0000 den= 10000 -7.0000 -16.0000 -18.0000 NUM=0 2.0000 140000 180000 0 2.0000 36.0000 14.0000 den= 1.0000-7.0000-16.0000-18.0000 31s2+40s+36 2s2+14s+18 即:W(s)= .s3-7s2-165-18 s3-7s2-16s-18 3.由系统的闭环传递函数转换为对角标准型 函数格式为:R,R,K-residue(num,den) 其中:P表示[9c2.cn了,R表示[A乃.n了,K表示d 例如: Y(s) 25+1 -7/6.3/2,-/3 U(s)s3+7s2+14s+8s+4s+2s+1 程序为: [a.b.c]-residue([1].[171481) A=diag(b) %生成对角阵 B=ones(length(a),1) %生成length(a)×1的全1阵 C=rot90(a) %矩阵转秩 D=c 运行结果为: A=-4.0000 0 0 B=1C=-1.16671.5000-0.3333 D-0 0 -2.0000 0 0 0 -1.0000 四、实验报告 1.记录或拷贝所分析系统的各种计算结果 41
现代控制理论实验 41 [NUM,den]=ss2tf(a,b,c,d,1) [NUM,den]=ss2tf(a,b,c,d,2) 运行结果为: NUM = 0 31.0000 40.0000 36.0000 1.0000 45.0000 32.0000 88.0000 den = 1.0000 -7.0000 -16.0000 -18.0000 NUM = 0 2.0000 14.0000 18.0000 0 2.0000 36.0000 14.0000 den = 1.0000 -7.0000 -16.0000 -18.0000 即: − − − + + − − − + + + − − − + + − − − + + = 7 16 18 2 36 14 7 16 18 45 32 88 7 16 18 2 14 18 7 16 18 31 40 36 ( ) 3 2 2 3 2 3 2 3 2 2 3 2 2 s s s s s s s s s s s s s s s s s s s s s W s 3.由系统的闭环传递函数转换为对角标准型 d s c d s c s c s c U s Y s n i i i n n + − + = − + + − + − = 2 =1 2 1 1 ( ) ( ) 函数格式为:[P,R,K]=residue(num,den) 其中:P 表示 T n c c c 1 2 ,R 表示 T 1 2 n ,K 表示 d 例如: 1 1 3 2 3 2 4 7 6 7 14 8 2 1 ( ) ( ) 3 2 + − + + + + − = + + + + = s s s s s s s U s Y s 程序为: [a,b,c]=residue([2 1],[1 7 14 8]); A=diag(b) %生成对角阵 B=ones(length(a),1) %生成 length(a)×1 的全 1 阵 C=rot90(a) %矩阵转秩 D=c 运行结果为: 四、实验报告 1.记录或拷贝所分析系统的各种计算结果; A = -4.0000 0 0 0 -2.0000 0 0 0 -1.0000 B= 1 1 1 C =-1.1667 1.5000 -0.3333 D= []

现代控制理论实验 2.利用MATLAB编制程序完成下列作业: 式已知系统的动态特性是由下列微分方程或传递函数描述,试建立其状态空间表 ①岁+35+2)+y=i+2i+u ②W(s)= 10(s-1) s(s+1)s+3) 2s3+4s2+3s+6 ③W(s)= 53+4s2+5s+3 (2)试求下列状态空间表达式的传递函数(阵) 。 y=0小 「41-2]「31 =102x+27 ② 1-1353 (3)试建立其对角标准型 W(s)= 10(s-1) s(5+1(s+3) 五、实验分析 用MATLAB命令转换的状态空间表达式与课本里介绍的方法有何异同,为什么?
现代控制理论实验 42 2.利用 MATLAB 编制程序完成下列作业: (1)已知系统的动态特性是由下列微分方程或传递函数描述,试建立其状态空间表 达式 ① y + 3 y + 2y + y = u + 2u + u ② ( 1)( 3) 10( 1) ( ) + + − = s s s s W s ③ 4 5 3 2 4 3 6 ( ) 3 2 3 2 + + + + + + = s s s s s s W s (2) 试求下列状态空间表达式的传递函数(阵) ① y x x x 1 0 1 0 1 2 2 1 = + − − = u ② y x x x = + − − = 0 1 1 1 2 0 5 3 2 7 3 1 1 1 3 1 0 2 4 1 2 u (3)试建立其对角标准型 ( 1)( 3) 10( 1) ( ) + + − = s s s s W s 五、实验分析 用 MATLAB 命令转换的状态空间表达式与课本里介绍的方法有何异同,为什么?

现代控制理论实验 实验二用MATLAB:求线性定常系统状态空间表达式的解 一、实验目的 1.学习ATLAB语言中常用命令: 2.利用MATLAB编程完成线性定常系统状态空间表达式的求解: 3.进一步加深对所学理论的理解 二、主要实验设备及仪器 1.计算机一台 2.MATLAB软件 三、实验内容 l.MATLAB中的step,impulse和initial函数分别用来求连续系统的单位阶跃响 应,单位脉冲响应和零输入响应,因此,编写MATLAB程序是很简单的。 函数格式为:step(num,den) step(A,B,C,D) 其中,subplot(1,3)表示所绘制的图形放在一行三列的第一列,plot(y选项) 用于在图形窗口上绘制所需的二维图形(选项:b一蓝,g一绿,一红,*一星号线,。 一圆圈线)。 例题1: 例题2: 例题3: a=01;-2-2] a=04;-2-2 a=01;-2-2 b=0122 b=01 b=01:10 c12:02: c=121: c12 d=[13,041 d-0 d[00: x0=[122, x0=[121' x0=[12' subplot(1,3,1) subplot(1,3,1) subplot(3.1.1) step(a b.c.d) step(ab.c,d) step(a.b.c.d) subplot(1,3.2) subplot(1,3,2) subplot(3,1.2) impulse(a.b.c.d) mpulse(a b.c.d) impulse(a b.c.d) subplot(1.3.3) subplot(1.3.3) subplot(3.1.3) initial(a.b.c,d,x0) initial(a,b.c.d.x0) initial(ab.c,d,x0) 运行结果为:如图21 运行结果为:如图2-2 运行结果为:如图2-3
现代控制理论实验 43 实验二 用MATLAB求线性定常系统状态空间表达式的解 一、实验目的 1.学习MATLAB语言中常用命令; 2.利用MATLAB编程完成线性定常系统状态空间表达式的求解; 3.进一步加深对所学理论的理解; 二、主要实验设备及仪器 1.计算机一台 2.MATLAB软件 三、实验内容 1.MATLAB中的step,impulse和initial函数分别用来求连续系统的单位阶跃响 应,单位脉冲响应和零输入响应,因此,编写MATLAB程序是很简单的。 函数格式为:step(num,den) step(A,B,C,D) 其中,subplot(1,3,1)表示所绘制的图形放在一行三列的第一列,plot(x,y,’选项’) 用于在图形窗口上绘制所需的二维图形(选项:b—蓝,g—绿,r—红,*—星号线,。 —圆圈线.)。 例题1: a=[0 1 ;-2 -2]; b=[0 1;2 2]'; c=[1 2;0 2]; d=[1 3;0 4]; x0=[12 2]'; subplot(1,3,1) step(a,b,c,d) subplot(1,3,2) impulse(a,b,c,d) subplot(1,3,3) initial(a,b,c,d,x0) 运行结果为:如图2-1 例题2: a=[0 4 ;-2 -2]; b=[0 1]'; c=[1 2]; d=0; x0=[1 2]'; subplot(1,3,1) step(a,b,c,d) subplot(1,3,2) mpulse(a,b,c,d) subplot(1,3,3) initial(a,b,c,d,x0) 运行结果为:如图2-2 例题3: a=[0 1 ;-2 -2]; b=[0 1;1 0]'; c=[1 2]; d=[0 0]; x0=[1 2]'; subplot(3,1,1) step(a,b,c,d) subplot(3,1,2) impulse(a,b,c,d) subplot(3,1,3) initial(a,b,c,d,x0) 运行结果为:如图2-3
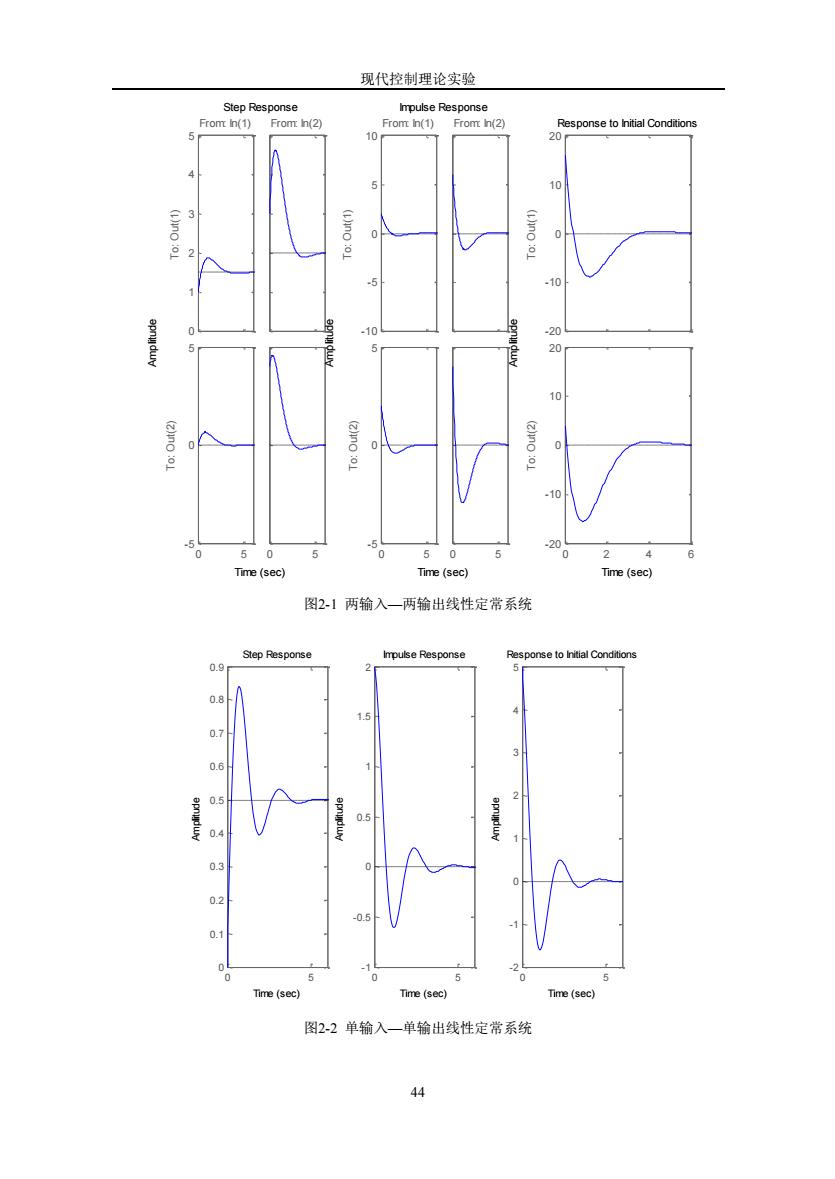
现代控制理论实验 Impulse Response From in(1) 图21两输入一两输出线性定常系统 图22单输入一单输出线性定常系统
现代控制理论实验 44 0 1 2 3 4 5 To: Out(1) From: In(1) 0 5 - 5 0 5 To: Out(2) From: In(2) 0 5 -10 - 5 0 5 10 To: Out(1) From: In(1) 0 5 - 5 0 5 To: Out(2) From: In(2) 0 5 -20 -10 0 10 20 To: Out(1) 0 2 4 6 -20 -10 0 10 20 To: Out(2) Step Response Time (sec) Amplitude Impulse Response Time (sec) Amplitude Response to Initial Conditions Time (sec) Amplitude 图2-1 两输入—两输出线性定常系统 0 5 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0 5 -1 -0.5 0 0.5 1 1.5 2 0 5 -2 -1 0 1 2 3 4 5 Step Response Time (sec) Amplitude Impulse Response Time (sec) Amplitude Response to Initial Conditions Time (sec) Amplitude 图2-2 单输入—单输出线性定常系统
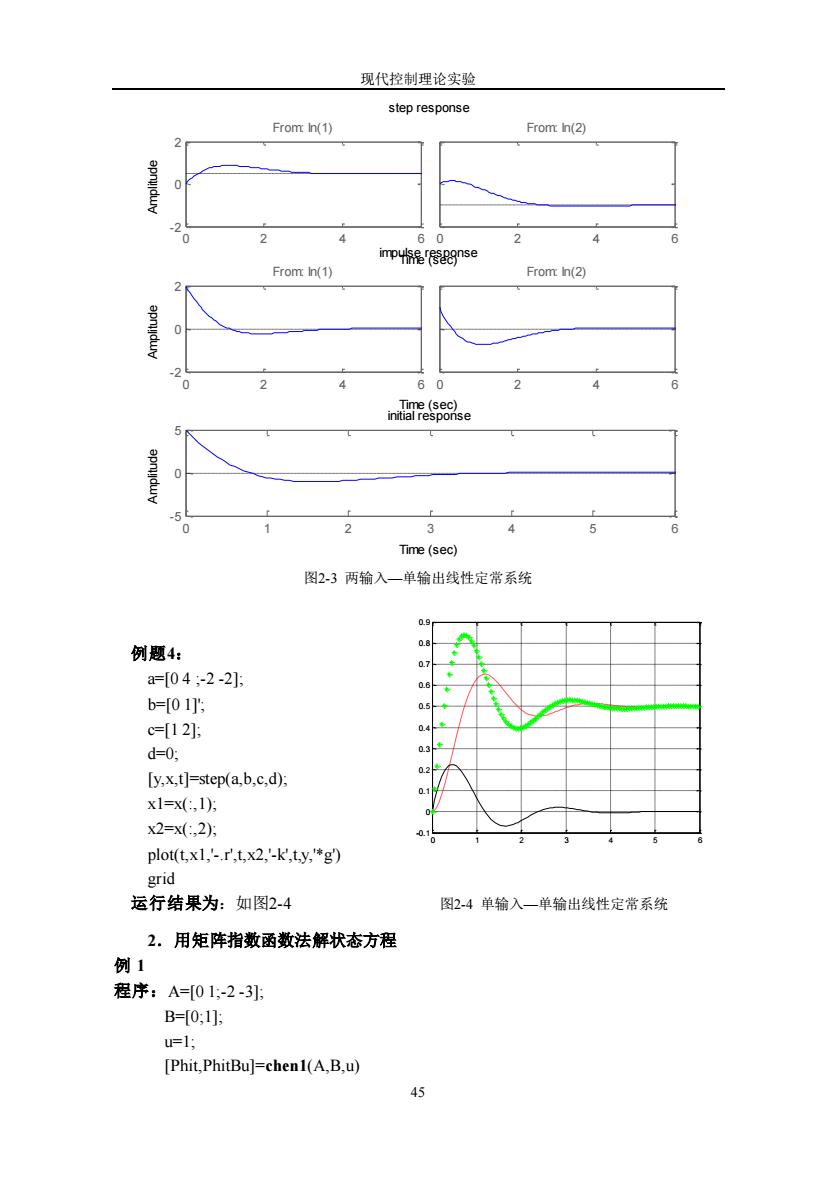
现代控制理论实验 step response From h(1) From n(② 2 4 2 4 imp4nse From h(1) From (2) nise 2 4 Time (sec) 图23两输入一单输出线性定常系统 09 08 例题4: 07 a=04;-2-21: b=01'. c=[12: d-0; [y.x.t]-step(a.b.c.d). 01 x1=x(,1: x2=x,2 01 plot(t.x1.'-.r.t.x2.'-k.ty,*g) 运行结果为:如图2-4 图24单输入一单输出线性定常系统 2.用矩阵指数函数法解状态方程 例1 程序:A=01,-2-3引 B=0:1: =1: [Phit.PhitBu]=chen1(A.B.u)
现代控制理论实验 45 0 2 4 6 - 2 0 2 From: In(1) 0 2 4 6 From: In(2) 0 2 4 6 - 2 0 2 From: In(1) 0 2 4 6 From: In(2) 0 1 2 3 4 5 6 - 5 0 5 step response Time (sec) Amplitude impulse response Time (sec) Amplitude initial response Time (sec) Amplitude 图2-3 两输入—单输出线性定常系统 例题4: a=[0 4 ;-2 -2]; b=[0 1]'; c=[1 2]; d=0; [y,x,t]=step(a,b,c,d); x1=x(:,1); x2=x(:,2); plot(t,x1,'-.r',t,x2,'-k',t,y,'*g') grid 运行结果为:如图2-4 图2-4 单输入—单输出线性定常系统 2.用矩阵指数函数法解状态方程 例 1 程序:A=[0 1;-2 -3]; B=[0;1]; u=1; [Phit,PhitBu]=chen1(A,B,u) 0 1 2 3 4 5 6 -0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

现代控制理论实验 x0=[1;2];x=Phit*x0+PhitBu chen1为下列函数文件的文件名。 function [Phit,PhitBu]=vsolvel(A,B,ut) 影求解线性连续系统状态方程X'=AX的解 %[Phit,PhitBu]=vsolvel(A,B,ut) %A,B系数矩阵 ut控制输入,必须为时域信号的符号表达式,符号变量为t syms t tao Phit=expm(A#t) if(B=-0) B=zero(size(A,1),1): end phi=subs(Phit,'t','t-tao'):Rexp[A(t-tao) PhitBus=int(phi*B知t,'tao',0,'t'):%求ep[A(t-tao)]相*u(tao)在0-t区间的积分 运行结果 Phit=-exp(-2*t)+2*exp(-t), exp(-t)-exp(-2*t)] [-2*exp(-t)+2*exp(-2*t), 2*exp(-2*)-exp(-t PhitBu=1/2-exp(-t)+1/2*exp(-2*t) exp(-t)-exp(-2*t) X= -5/2*exp(-2*t)+3*exp(-t)+1/2 -3*exp(-r5*exp(-2*) 例2 程序:A=01:00: B=0,1 =l: [Phit.PhitBu]=chen1(A.B.u) x0=[1;1];x=Phit*x0+PhitBu 运行结果: Phit=[l,t可 [01] PhitBu=1/2*t2 t x=1+t+1/2*t2 1+t
现代控制理论实验 46 x0=[1;2];x=Phit*x0+PhitBu chen1 为下列函数文件的文件名。 function[Phit,PhitBu]=vsolvel(A,B,ut) %求解线性连续系统状态方程X'=AX的解 %[Phit,PhitBu]=vsolvel(A,B,ut) %A,B系数矩阵 %ut控制输入,必须为时域信号的符号表达式,符号变量为t syms t tao Phit=expm(A*t); if(B==0) B=zero(size(A,1),1); end phi=subs(Phit,'t','t-tao');%求exp[A(t-tao)] PhitBu=int(phi*B*ut,'tao',0,'t');%求exp[A(t-tao)]*B*u(tao)在0-t区间的积分 运行结果: Phit = [ -exp(-2*t)+2*exp(-t), exp(-t)-exp(-2*t)] [ -2*exp(-t)+2*exp(-2*t), 2*exp(-2*t)-exp(-t)] PhitBu = 1/2-exp(-t)+1/2*exp(-2*t) exp(-t)-exp(-2*t) x = -5/2*exp(-2*t)+3*exp(-t)+1/2 -3*exp(-t)+5*exp(-2*t) 例 2 程序: A=[0 1;0 0]; B=[0;1]; u=1; [Phit,PhitBu]=chen1(A,B,u) x0=[1;1];x=Phit*x0+PhitBu 运行结果: Phit = [ 1, t] [ 0, 1] PhitBu = 1/2*t^2 t x = 1+t+1/2*t^2 1+t

现代控制理论实验 四、实验报告 1.记录或拷贝所分析系统的各种计算结果: 2.利用MATLAB编制程序完成下列作业: 试求下列状态空间表达式的单位阶跃响应,单位脉冲响应和零输入响应: ①岁+3莎+2)+y=i+2+u ②W(s)= 10(s-1) s(s+1(s+3) ③W(s)= 2s3+4s2+3s+6 s3+4s2+5s+3 「-211 「01 1-2+ y=o小 「41-2]「311 x=102x+27日 ⑤1-1353 12x y=01 五、实验分析 系统的稳定性是否与输入信号有关?
现代控制理论实验 47 四、实验报告 1.记录或拷贝所分析系统的各种计算结果; 2.利用MATLAB编制程序完成下列作业: 试求下列状态空间表达式的单位阶跃响应,单位脉冲响应和零输入响应: ① y + 3 y + 2y + y = u + 2u + u ② ( 1)( 3) 10( 1) ( ) + + − = s s s s W s ③ 4 5 3 2 4 3 6 ( ) 3 2 3 2 + + + + + + = s s s s s s W s ④ y x x x 1 0 1 0 1 2 2 1 = + − − = u ⑤ y x x x = + − − = 0 1 1 1 2 0 5 3 2 7 3 1 1 1 3 1 0 2 4 1 2 u 五、实验分析 系统的稳定性是否与输入信号有关 ?

现代控制理论实验 实验三线性定常系统的能控性、能观性判别 一、实验目的 1,学习MATLAB语言中常用命令: 2.利用MATLAB编程完成线性定常系统能控性、能观性的判别: 3.进一步加深对所学理论的理解: 二、主要实验设备及仪器 1.计算机一台 2.MATLAB软件 三、实验内容 MATLAB中的ctrb和obsw分别用来构造能控性判别矩阵M阵和能观性判别 矩阵N阵的,rank用来求M阵和N阵的秩。 函数格式为:M=ctbA.B) N=obsv(A,C) r=rank(M) 例如1:己知系统的传递函数为W(s)= +5x2+75+6试建立其状态空间表达 s2+2s+3 式,并判断其能控性、能观性。 num=[123: den=1576: [A BC D]=tf2ss(num,den) M=ctrb(A.B)】 N=obsv(A.C) p=rank(M) q=rank(N) 运行结果为: A=-5-7 -6B=1 C=1 2D=0 1 0 0 0 3 0 1 0 0 M=1-5 18 N=1 2 3p=3 q=3 0 .5 -3 .4 6 0 0 1 11 15 18 结论:由于M阵和N阵的秩都等于=3,所以系统是能控能观的。 e
现代控制理论实验 48 实验三 线性定常系统的能控性、能观性判别 一、实验目的 1.学习 MATLAB 语言中常用命令; 2.利用 MATLAB 编程完成线性定常系统能控性、能观性的判别; 3.进一步加深对所学理论的理解; 二、主要实验设备及仪器 1.计算机一台 2.MATLAB 软件 三、实验内容 MATLAB 中的 ctrb 和 obsv 分别用来构造能控性判别矩阵 M 阵和能观性判别 矩阵 N 阵的,rank 用来求 M 阵和 N 阵的秩。 函数格式为: M= ctrb (A,B) N=obsv (A,C) r=rank(M) 例如 1:已知系统的传递函数为 5 7 6 2 3 ( ) 3 2 2 + + + + + = s s s s s W s ,试建立其状态空间表达 式,并判断其能控性、能观性。 num=[1 2 3]; den=[1 5 7 6]; [A B C D]=tf2ss(num,den) M=ctrb(A,B) N=obsv(A,C) p=rank(M) q=rank(N) 运行结果为: A = -5 -7 -6 1 0 0 0 1 0 B = 1 0 0 C = 1 2 3 D = 0 M = 1 -5 18 0 1 -5 0 0 1 N = 1 2 3 -3 -4 -6 11 15 18 p = 3 q = 3 结论:由于 M 阵和 N 阵的秩都等于 n=3,所以系统是能控能观的