
第四章根轨迹法 在时域分析法中己知控制系统的闭环特征根决定该控制系统的性能。那么,是 否对于每一个控制系统都必须求出其闭环特征根,才能够了解其性能呢?如果答案 是背定的,那么当特征多项式是三阶及以上时,求解特征根是一项比较复杂的工作。 特别是要分析系统特征式中某一参数(比如K)变化时对系统性能的影响,这种准 确求解每一个特征根的工作将会变得十分困难。 W.R.Evans提出了一种描述特征方程中某一参数与该方程特征根之间对应关系 的图解法,比较方便的解决了上述问题。这种方法就是本章要介绍的根轨迹法。 4.1根轨迹的基本概念 1.根轨迹的定义 系统参数(如开环增益K)由0→∞变化时,闭环特征根在s平面移动的轨迹 称为该系统的闭环根轨迹。 [例4单位反馈控制系统如图,绘制K变化时,系统极点的变化情况。 R,⑧ K☐Cs) s0.5s+1 C(s) 2K* R6g2+25+2K 特征方程 D(s)=s2+25+2K°=0 特征根 52=-1±V-2K 讨论当K=0时, 31=0,32=-2 K=0.5时,31=52=-1 K=1时, 52=-1±1 K→o时,2=-1土j0,绘出特征根的变化轨迹如图 0
41 第四章 根轨迹法 在时域分析法中已知控制系统的闭环特征根决定该控制系统的性能。那么,是 否对于每一个控制系统都必须求出其闭环特征根,才能够了解其性能呢?如果答案 是肯定的,那么当特征多项式是三阶及以上时,求解特征根是一项比较复杂的工作。 特别是要分析系统特征式中某一参数(比如 K*)变化时对系统性能的影响,这种准 确求解每一个特征根的工作将会变得十分困难。 W.R.Evans 提出了一种描述特征方程中某一参数与该方程特征根之间对应关系 的图解法,比较方便的解决了上述问题。这种方法就是本章要介绍的根轨迹法。 4.1 根轨迹的基本概念 1.根轨迹的定义 系统参数(如开环增益 K )由 0→∞变化时,闭环特征根在 s 平面移动的轨迹 称为该系统的闭环根轨迹。 [例 4-1] 单位反馈控制系统如图,绘制 K*变化时,系统极点的变化情况。 2 * * 2 2 2 ( ) ( ) s s K K R s C s + + = 特征方程 ( ) 2 2 0 2 * D s = s + s + K = 特征根 * s1,2 = −1 1− 2K 讨论 当 0 * K = 时, s1 = 0 , s2 = −2 0.5 * K = 时, s1 = s2 = −1 1 * K = 时, s1,2 = −1 j1 → * K 时, s1,2 = −1 j ,绘出特征根的变化轨迹如图 jω × × s(0.5s 1) K + R(s) C(s) -2 -1 0

显然,当00.5时,系统取得一对共轭复数根(欠阻尼)。 越大,共轭复数根离对称轴(实轴)越远. 指定一个K'值,就可以在根轨迹上找到对应的二个特征根,指定根轨迹上任意 一特征根的位置,就可以求出该特征根对应的K值和其余特征根。下面我们讨论根 轨迹的一般情况 2.根轨迹方程及幅值条件、相角条件 既然根轨迹是闭环特征根随参数变化的轨迹,则描述其变化关系的闭环特征方 程就是根轨迹方程。 设系统开环传递函数为 K'I(s-=) G(s)H(s)= (4-1) [I-p) 其中,K称为根轨迹增益:二,是开环零点:P,是开环极点。 则根轨迹方程(系统闭环特征方程)为 1+G(s)H(s)=0 K'II(s-=) 即 -1 (4-2) Πs-p,) 显然,满足上式的s即是系统的闭环特征根。 当K`从0变化到∞时,n个特征根将随之变化出n条轨迹。这n条轨迹就是系 统的闭环根轨迹(简称根轨迹)。 由式(4-2)确定的根轨迹方程可以分解成相角条件和幅值条件 三4+24+p)-空0-2a,=±2k+r (4-3)
42 显然,当 0 0.5 * K 时,系统取得二不相等实数根(过阻尼); 0.5 * K = 时,系统取得二相等实数根(临界阻尼); 0.5 * K 时,系统取得一对共轭复数根(欠阻尼)。 * K 越大,共轭复数根离对称轴(实轴)越远. 指定一个 * K 值,就可以在根轨迹上找到对应的二个特征根,指定根轨迹上任意 一特征根的位置,就可以求出该特征根对应的 * K 值和其余特征根。下面我们讨论根 轨迹的一般情况。 2.根轨迹方程及幅值条件、相角条件 既然根轨迹是闭环特征根随参数变化的轨迹,则描述其变化关系的闭环特征方 程就是根轨迹方程。 设系统开环传递函数为 = = − − = n j i m i i s p K s z G s H s 1 1 * ( ) ( ) ( ) ( ) (4-1) 其中, * K 称为根轨迹增益; i z 是开环零点; j p 是开环极点。 则根轨迹方程(系统闭环特征方程)为 1+ G(s)H(s) = 0 即 1 ( ) ( ) 1 1 * = − − − = = n j j m i i s p K s z (4-2) 显然,满足上式的 s 即是系统的闭环特征根。 当 * K 从 0 变化到∞时,n 个特征根将随之变化出 n 条轨迹。这 n 条轨迹就是系 统的闭环根轨迹(简称根轨迹)。 由式(4-2)确定的根轨迹方程可以分解成相角条件和幅值条件 ( ) ( ) (2 1) 1 1 1 1 + − + = − = + = = = = s z s p k m i n l i l m i n l i l (4-3)

K'IIls-=l (44) -p叭 几点说明: 1.开环零点、极点p是决定闭环根轨迹的条件。 2.注意到式(4-3)定义的相角条件不含有K,它表明满足式(44)的任意K值均满 足由相角条件定义的根轨迹,因此,相角条件是决定闭环根轨迹的充分必要条件。 3.满足相角条件的闭环极点s值,代入幅值条件式(44),就可以求出对应的K值, 显然一个K'对应个3值,满足幅值条件的s值不一定满足相角条件。因此由幅值 条件(及其变化式)求出的5值不一定是根轨迹上的根。 任意特征方程D(s)=0均可处理成1+G(s)H(s)=0的形式,其中把 G(s)H(s)写成式(4-4)描述的形式就可以得到K`值,所以说K可以是系统任意参 数。以其它参数为自变量作出的根轨迹称广义根轨迹。 4.2绘制根轨迹的基本规则 规则1根轨迹的对称性:相对于实轴对称 规则2根轨迹的分支数及其起点和终点: 根轨迹的分支数为n个:根轨迹起始于开环极点,终止于开环零点(包括无限 远零点)。 规则3根轨迹在实轴上的分布 实轴上有根轨迹的区段为右侧的开环实极点与开环实零点数目之和为奇数。 规则4根轨迹的渐近线:(当n-m≥2时) 与实轴交点坐标 -0,岛 (4-5) 与实轴正方向的夹角 0=于2k+1z (4-6) n-m 式中k依次取01,2一直到获得(n-m)个倾角为止。 规则5根轨迹的分离点(或汇合点):
43 1 1 1 * = − − = = n j j m i i s p K s z (4-4) 几点说明: 1. 开环零点 zi、极点 pj 是决定闭环根轨迹的条件。 2.注意到式(4-3)定义的相角条件不含有 * K ,它表明满足式(4-4)的任意 * K 值均满 足由相角条件定义的根轨迹,因此,相角条件是决定闭环根轨迹的充分必要条件。 3.满足相角条件的闭环极点 s 值,代入幅值条件式(4-4),就可以求出对应的 * K 值, 显然一个 * K 对应 n 个 s 值,满足幅值条件的 s 值不一定满足相角条件。因此由幅值 条件(及其变化式)求出的 s 值不一定是根轨迹上的根。 任意特征方程 D(s) = 0 均可处理成 1+ G(s)H(s) = 0 的形式,其中把 G(s)H(s) 写成式(4-4)描述的形式就可以得到 * K 值,所以说 * K 可以是系统任意参 数。以其它参数为自变量作出的根轨迹称广义根轨迹。 4.2 绘制根轨迹的基本规则 规则 1 根轨迹的对称性:相对于实轴对称; 规则 2 根轨迹的分支数及其起点和终点: 根轨迹的分支数为 n 个;根轨迹起始于开环极点,终止于开环零点(包括无限 远零点)。 规则 3 根轨迹在实轴上的分布 实轴上有根轨迹的区段为右侧的开环实极点与开环实零点数目之和为奇数。 规则 4 根轨迹的渐近线:(当 n − m 2 时) 与实轴交点坐标 n m p z m i i n l l A − − − − − = =1 =1 ( ) ( ) (4-5) 与实轴正方向的夹角 ( ) n m k − + = 2 1 (4-6) 式中 k 依次取 0,1,2 一直到获得( n − m )个倾角为止。 规则 5 根轨迹的分离点(或汇合点):

(1)不是所有的系统在绘制根轨迹时,都要求分离点(或汇合点):只有当两 个开环极点之间有根轨迹时,才存在分离点:当两个开环零点(包括一个无限零点) 之间有根轨迹时,则存在汇合点:当一个开环极点和一个开环零点(可以是无限零 点)之间有根轨迹时,一般没有分离点,若有,则必然是成对出现的。 (2)根轨迹的分离点(或汇合点)的求取: 若令系统的开环传递函数为:G6H)=K,B A(s) 则 dK=0,或 ds A(s)B'(s)-A(s)B(s)=0 (47) 根轨迹的分离点(或汇合点)是A(s)B'(s)-A(s)B(s)=0的根, (3)满足As)B'(s)-A"(s)B(s)=0的根不一定都是根轨迹的分离点(或汇合 点),分离点(或汇合点)必须在根轨迹上:如果有的根不在根轨迹上,则应该舍去。 规则6根轨迹与虚轴的交点 (1)当根轨迹可能和虚轴相交时,需要求根轨迹与虚轴的交点:否则,无需求 取。 (2)根轨迹与虚轴的交点的求取: ①由劳斯判据可求得交点的坐标及相应的K。值: ②在特征方程中,令5=0,然后使特征方程的实部和虚部分别为零,可求得交点 的坐标及相应的K。=K,值。 ③根轨迹和虚轴交点处相当于系统处于临界稳定状态。此时增益K,称为临界根轨迹 增益。 规则7根轨迹的出射角和入射角 系统中存在开环共轭复极点(或复零点)时,需要求出射角和入射角。 出射角: 0,=2k+1)z+∑0,-∑0 (4-8) 入射角: 9=2k+r+20,-20 (49) 典型开环极点、零点分部及其相应的根轨迹如表4-1所示
44 (1)不是所有的系统在绘制根轨迹时,都要求分离点(或汇合点);只有当两 个开环极点之间有根轨迹时,才存在分离点;当两个开环零点(包括一个无限零点) 之间有根轨迹时,则存在汇合点;当一个开环极点和一个开环零点(可以是无限零 点)之间有根轨迹时,一般没有分离点,若有,则必然是成对出现的。 (2)根轨迹的分离点(或汇合点)的求取: 若令系统的开环传递函数为: ( ) ( ) ( ) ( ) 0 A s K B s G s H s = 则 0 0 = ds dK ,或 A(s)B(s) − A(s)B(s) = 0 (4-7) 根轨迹的分离点(或汇合点)是 A(s)B(s) − A(s)B(s) = 0 的根, (3)满足 A(s)B(s) − A(s)B(s) = 0 的根不一定都是根轨迹的分离点(或汇合 点),分离点(或汇合点)必须在根轨迹上;如果有的根不在根轨迹上,则应该舍去。 规则 6 根轨迹与虚轴的交点 (1)当根轨迹可能和虚轴相交时,需要求根轨迹与虚轴的交点;否则,无需求 取。 (2)根轨迹与虚轴的交点的求取: ①由劳斯判据可求得交点的坐标及相应的 K0 值; ②在特征方程中,令 s = j ,然后使特征方程的实部和虚部分别为零,可求得交点 的坐标及相应的 K0 = Kl 值。 ③根轨迹和虚轴交点处相当于系统处于临界稳定状态。此时增益 Kl 称为临界根轨迹 增益。 规则 7 根轨迹的出射角和入射角 系统中存在开环共轭复极点(或复零点)时,需要求出射角和入射角。 出射角: = = = + + − m i n j l j l i j k 1 1 (2 1) (4-8) 入射角: = = = + + − n j m i l i k j i k 1 1 (2 1) (4-9) 典型开环极点、零点分部及其相应的根轨迹如表 4-1 所示
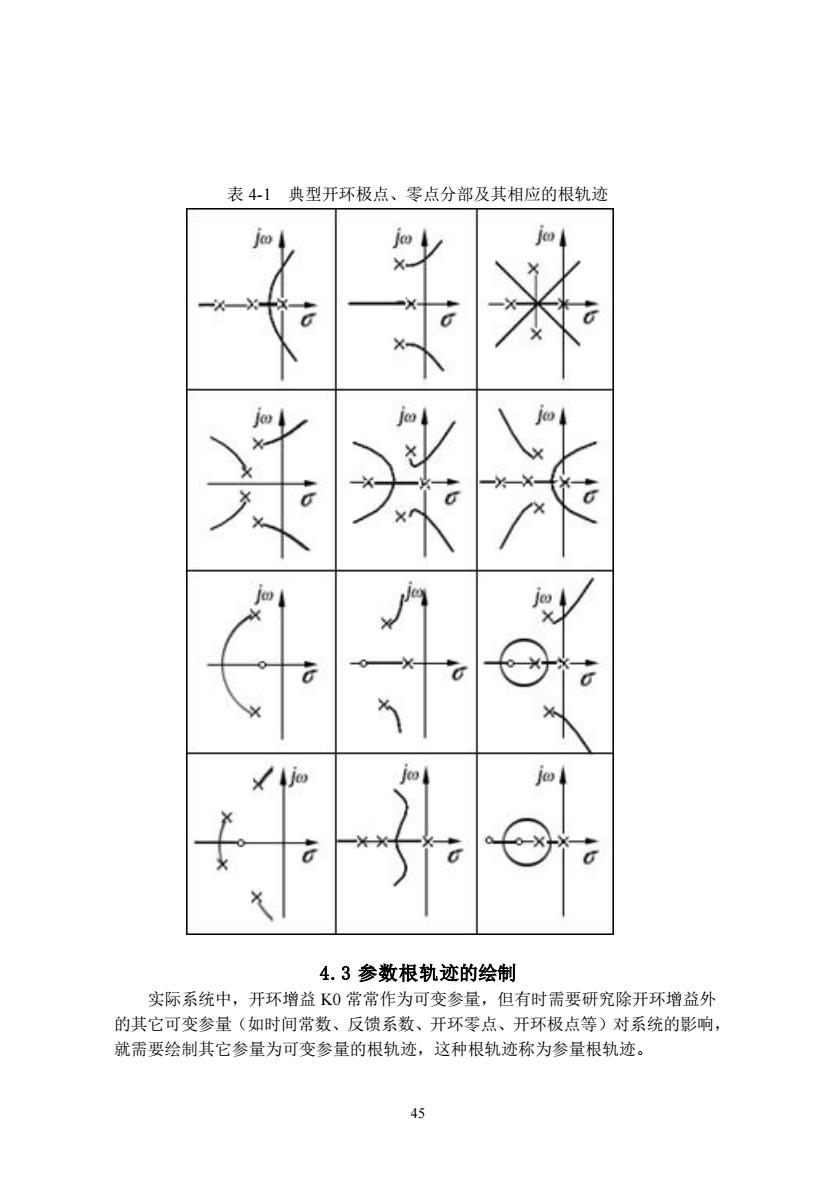
表41典型开环极点、零点分部及其相应的根轨迹 4.3参数根轨迹的绘制 实际系统中,开环增益K0常常作为可变参量,但有时需要研究除开环增益外 的其它可变参量(如时间常数、反馈系数、开环零点、开环极点等)对系统的影响 就需要绘制其它参量为可变参量的根轨迹,这种根轨迹称为参量根轨迹
45 表 4-1 典型开环极点、零点分部及其相应的根轨迹 4.3 参数根轨迹的绘制 实际系统中,开环增益 K0 常常作为可变参量,但有时需要研究除开环增益外 的其它可变参量(如时间常数、反馈系数、开环零点、开环极点等)对系统的影响, 就需要绘制其它参量为可变参量的根轨迹,这种根轨迹称为参量根轨迹

思路:由于根轨迹是利用系统开环传递函数的零点和极点绘制出的,因此将特 征方程式等效变换,导出等效的开环传递函数(此时,需要研究的其它可变参量的 位置与K0相当。),然后再利用根轨迹绘制法则绘制参量根轨迹。 例:设位置随动如图所示,试绘制 以Td为参变量的根轨迹。 R(s) 解:系统的开环传递函数为 +5(1+1s G(s)H(s)=5(L+T,s) s(5s+1) 特征方程式为:l+G(s)H(s)=0→s(5s+)+51+Ts)=0 G(6Hs数=g+02s+1s+0.1-s+0.1+) 4.4非最小相位系统的根轨迹 开环传递函数的零点、极点均位于s左半平面的系统,称为最小相位系统:反 之,则称为非最小相位系统 在控制工程中出现的非最小相位系统,通常为如下三种情况: 1.系统中存在着局部的正反馈回路。 2.系统中含有非最小相位元件。 3系统中含有滞后环节。 正反馈回路回路的根轨迹 C(s) JS)) 内回路的闭环传递函数为 R(s)1-G(s)H(s) 相应的特征方程式为 1-G(s)H(s)=0→G(s)H(s)=1
46 思路:由于根轨迹是利用系统开环传递函数的零点和极点绘制出的,因此将特 征方程式等效变换,导出等效的开环传递函数(此时,需要研究的其它可变参量的 位置与 K0 相当。),然后再利用根轨迹绘制法则绘制参量根轨迹。 例:设位置随动如图所示,试绘制 以 Td 为参变量的根轨迹。 解:系统的开环传递函数为 4.4 非最小相位系统的根轨迹 开环传递函数的零点、极点均位于 s 左半平面的系统,称为最小相位系统;反 之,则称为非最小相位系统 在控制工程中出现的非最小相位系统,通常为如下三种情况: 1.系统中存在着局部的正反馈回路。 2 .系统中含有非最小相位元件。 3 .系统中含有滞后环节。 正反馈回路回路的根轨迹 内回路的闭环传递函数为 相应的特征方程式为 (5 1) 1 s s + 5(1+Tds) R(s) C(s) (5 1) 5(1 ) ( ) ( ) + + = s s T s G s H s d 特征方程式为:1+G(s)H(s) = 0 s(5s +1)+5(1+Td s) = 0 j 0 Td=1.3 -1 1−G(s)H(s) = 0 G(s)H(s) =1 . ( . )( . ) ( ) ( ) s j s j T s s s T s G s H s d d + − + + + + = 0 2 1 0 1 0 1 等效 2 1 ( ) ( ) ( ) ( ) ( ) G s H s G s R s C s − =

KoIIs+ |G(s)H(s)= =1k=0,1,2,. IIs+pl ∠Gs)H6)=∑4s+)-2∠6+p,)=±2kx k=0,1,2,. 幅值条件没有变化,相角条件有变化,因此绘制根轨迹的规则相应变化。 规则3根轨迹在实轴上的分布 实轴上有根轨迹的区段为右侧的开环实极点与开环实零点数目之和为偶数。 规则4根轨迹的渐近线:(当n-m≥2时) 与实轴正方向的夹角 0=F2kn (410) n-m 式中k依次取0,L2一直到获得(n-m)个倾角为止。 规则7根轨迹的出射角和入射角 出射角: 8,=2kr+∑g,-∑0 (411) i=l 入射角: a=2kr+∑0,-2% (4-12) 4.5控制系统根轨迹的性能分析 根轨迹法在系统分析中的应用是多方面的,在参数己知的情况下求系统的特性: 分析参数变化对系统特性的影响(即系统特性对参数变化的敏感度和添加零,极点 对根轨迹的影响):对于高阶系统,运用“主导极点”概念,快速估价系统的基本特 性等 系统的暂态特性取决于闭环零、极点的分布,因而和根轨迹的形状密切相关。 而根轨迹的形状又取决于开环零、极点的分布。那么开环零、极点对根轨迹形状的 影响如何,这是单变量系统根轨迹法的一个基本问题。知道了闭环极点以及闭环零 点(通常闭环零点是容易确定的),就可以对系统的动态性能进行定性分析和定量计 算。 1.加开环极点对控制系统的影响 大量实例表明:增加位于s左半平面的开环极点,将使根轨迹向右半平面移动, 系统的稳定性能降低。例如,设系统的开环传递函数为
47 幅值条件没有变化,相角条件有变化,因此绘制根轨迹的规则相应变化。 规则 3 根轨迹在实轴上的分布 实轴上有根轨迹的区段为右侧的开环实极点与开环实零点数目之和为偶数。 规则 4 根轨迹的渐近线:(当 n − m 2 时) 与实轴正方向的夹角 n m k − = 2 (4-10) 式中 k 依次取 0,1,2 一直到获得( n − m )个倾角为止。 规则 7 根轨迹的出射角和入射角 出射角: = = = + − m i n j l j l i j k 1 1 2 (4-11) 入射角: = = = + − n j m i l i k j i k 1 1 2 (4-12) 4.5 控制系统根轨迹的性能分析 根轨迹法在系统分析中的应用是多方面的,在参数已知的情况下求系统的特性; 分析参数变化对系统特性的影响(即系统特性对参数变化的敏感度和添加零,极点 对根轨迹的影响);对于高阶系统,运用“主导极点”概念,快速估价系统的基本特 性等。 系统的暂态特性取决于闭环零、极点的分布,因而和根轨迹的形状密切相关。 而根轨迹的形状又取决于开环零、极点的分布。那么开环零、极点对根轨迹形状的 影响如何,这是单变量系统根轨迹法的一个基本问题。知道了闭环极点以及闭环零 点(通常闭环零点是容易确定的),就可以对系统的动态性能进行定性分析和定量计 算。 1. 加开环极点对控制系统的影响 大量实例表明:增加位于 s 左半平面的开环极点,将使根轨迹向右半平面移动, 系统的稳定性能降低。例如,设系统的开环传递函数为 ( ) ( ) 1 0,1,2, 1 1 0 = = + + = = = k s p K s z G s H s n j j m i i ( ) ( ) ( ) ( ) 2 0,1,2, 1 1 = + − + = = = = G s H s s z s p k k j n j i m i

G(s)=-K a1>0 (4-13) s(s+a) 则可绘制系统的根轨迹,如图41(a)所示。若增加一个开环极点P,=a2,根据这时 的开环传递函数 (s)= a2>0 (4-14) s(s+a)(s+az) 可绘制系统的根轨迹,如图49b)所示。 6 图41增加开环极点对根轨迹的影响 (a) (b) 图42增加开环零点对根轨迹的影响 由图可见:增加开环极点,使根轨迹的复数部分向右半平面弯曲。若取☑=1、 a2=2,则渐近线的倾角由原米的±90°变为±60°:分离点由原来的-0.5向右移至
48 ( ) ( ) 1 * s s a K G s k + = a1 0 (4-13) 则可绘制系统的根轨迹,如图 4-1(a)所示。若增加一个开环极点 p3 = a2 ,根据这时 的开环传递函数 Gk1 (s)= ( )( ) 1 2 1 s s a s a K + + a2 0 (4-14) 可绘制系统的根轨迹,如图 4-9(b)所示。 jω jω × × × × × (a) (b) 图 4-1 增加开环极点对根轨迹的影响 jω jω × × × × (a) (b) 图 4-2 增加开环零点对根轨迹的影响 由图可见:增加开环极点,使根轨迹的复数部分向右半平面弯曲。若取 a1 =1 、 a2 = 2 ,则渐近线的倾角由原来的 90 o 变为 60o;分离点由原来的-0.5 向右移至 –2 –1 0 -1 -2 -1

-0.422:与分离点相对应的开环增益,由原来的0.25(即K-0.5×0.5=-0.25)减少到 019(即K:-)×0,422×0.578×1.578-019)这意味着,对于具有同样的振荡倾 向,增加开环极点后使开环增益值下降。一般来说,增加的开环极点越靠近虚轴, 其影响越大,使根轨迹向右半平面弯曲就越严重,因而系统稳定性能的降低便越明 显。 2.增加开环零点对控制系统的影响 一般来说,开环传递函数G(s)H(s)增加零点,相当于引入微分作用,使根轨 迹向左半s平面移动,将提高系统的稳定性。例如,图42(a)表示式(4-13)增加 个零点:=-2的根轨迹(并设a=1),轨迹向左半s平面移动,且成为一个圆,结 果使控制系统的稳定性提高。图4-2(b)是式(4-13)增加一对共轭复数零点的根轨迹。 3.利用根轨迹确定系统参数 我们首先讨论当闭环特征根已经选定在根轨迹的某特定位置时如何确定应取的 参数值。由根轨迹的幅值条件,所有在根轨迹上的点必须满足 KΠ- =1 IIk-el 因此根据要求的闭环极点、一50可以由此求得应取的K'值。 [例42引设开环传递函数为 K G,(8)=s+4y+16 (415) 它的根轨迹如图4-3所示,要求闭环极点位于使系统具有5-0.5的阻尼比的位置, 那么增益K应是多大? 解在图43中画出5=0.5的射线,与根轨迹相交得闭环极点的要求位置5。 再画出G(S)的极点到5的三个向量一一+P,o+P2,56+P,由幅值条件 49
49 -0.422;与分离点相对应的开环增益,由原来的 0.25(即 * K =0.5 0.5=0.25)减少到 0.19(即 * K1 = 0.422 0.578 1.578 2 1 =0.19)这意味着,对于具有同样的振荡倾 向,增加开环极点后使开环增益值下降。一般来说,增加的开环极点越靠近虚轴, 其影响越大,使根轨迹向右半平面弯曲就越严重,因而系统稳定性能的降低便越明 显。 2.增加开环零点对控制系统的影响 一般来说,开环传递函数 G(s)H(s) 增加零点,相当于引入微分作用,使根轨 迹向左半 s 平面移动,将提高系统的稳定性。例如,图 4-2(a)表示式(4-13)增加一 个零点 z = −2 的根轨迹(并设 a1 =1 ),轨迹向左半 s 平面移动,且成为一个圆,结 果使控制系统的稳定性提高。图 4-2(b)是式(4-13)增加一对共轭复数零点的根轨迹。 3.利用根轨迹确定系统参数 我们首先讨论当闭环特征根已经选定在根轨迹的某特定位置时如何确定应取的 参数值。由根轨迹的幅值条件,所有在根轨迹上的点必须满足 1 1 1 * = − − = = n j j m i i s p K s z 因此根据要求的闭环极点 s=s0 可以由此求得应取的 * K 值。 [例 4-2] 设开环传递函数为 [( 4) 16] ( ) 2 * + + = s s K G s k (4-15) 它的根轨迹如图 4-3 所示,要求闭环极点位于使系统具有 = 0.5 的阻尼比的位置, 那么增益 * K 应是多大? 解 在图 4-3 中画出 = 0.5 的射线,与根轨迹相交得闭环极点的要求位置 0 s 。 再画出 G (s) k 的极点到 0 s 的三个向量—— 0 p1 s + , 0 p2 s + , 0 p3 s + ,由幅值条件
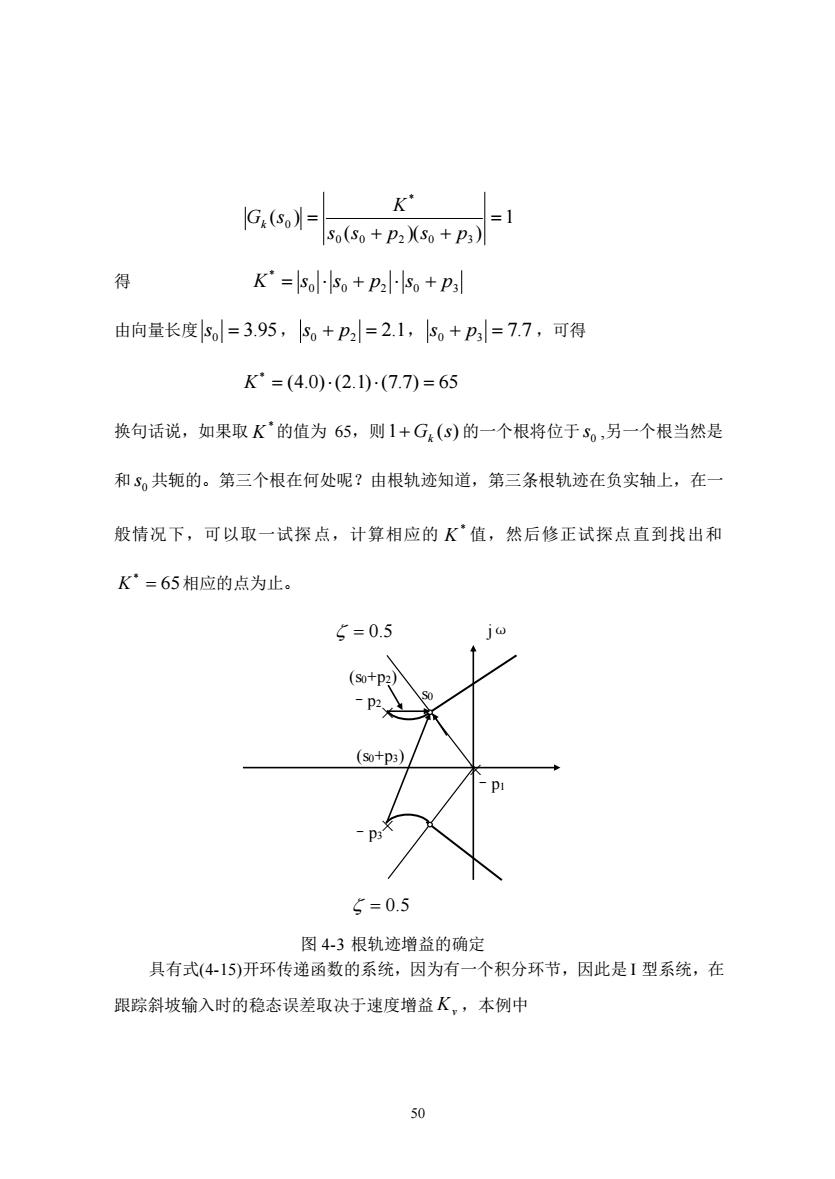
K .((p) 得 K"=Sol-so pa-so+pal 由向量长度=3.95,s+P=21,s+P3=7.7,可得 K=(4.0)-(2.1)-(7.7=65 换句话说,如果取K的值为65,则1+G(s)的一个根将位于S。,另一个根当然是 和3。共轭的。第三个根在何处呢?由根轨迹知道,第三条根轨迹在负实轴上,在 般情况下,可以取一试探点,计算相应的K值,然后修正试探点直到找出和 K=65相应的点为止。 5=0.5 5=0.5 图4-3根轨迹增益的确定 具有式(4-15)开环传递函数的系统,因为有一个积分环节,因此是1型系统,在 跟踪斜坡输入时的稳态误差取决于速度增益K,本例中
50 1 ( )( ) ( ) 0 0 2 0 3 * 0 = + + = s s p s p K G s k 得 0 0 2 0 3 * K = s s + p s + p 由向量长度 s0 = 3.95, s0 + p2 = 2.1, s0 + p3 = 7.7 ,可得 (4.0) (2.1) (7.7) 65 * K = = 换句话说,如果取 * K 的值为 65,则 1 G (s) + k 的一个根将位于 0 s ,另一个根当然是 和 0 s 共轭的。第三个根在何处呢?由根轨迹知道,第三条根轨迹在负实轴上,在一 般情况下,可以取一试探点,计算相应的 * K 值,然后修正试探点直到找出和 65 * K = 相应的点为止。 = 0.5 jω × = 0.5 图 4-3 根轨迹增益的确定 具有式(4-15)开环传递函数的系统,因为有一个积分环节,因此是 I 型系统,在 跟踪斜坡输入时的稳态误差取决于速度增益 Kv ,本例中 × × –p1 –p3 –p2 (s0+p2) (s0+p3) s0