新疆大学：《自动控制理论》课程教学课件（PPT讲稿）第八章 非线性控制系统

自动控制理论 第八章非线性控制系统 新疆大学电气工程学院 第八章非线性控制系统 2025/114

1 第八章 非线性控制系统 2025/1/14 第八章非线性控制系统 新疆大学 电气工程学院 自动控制理论

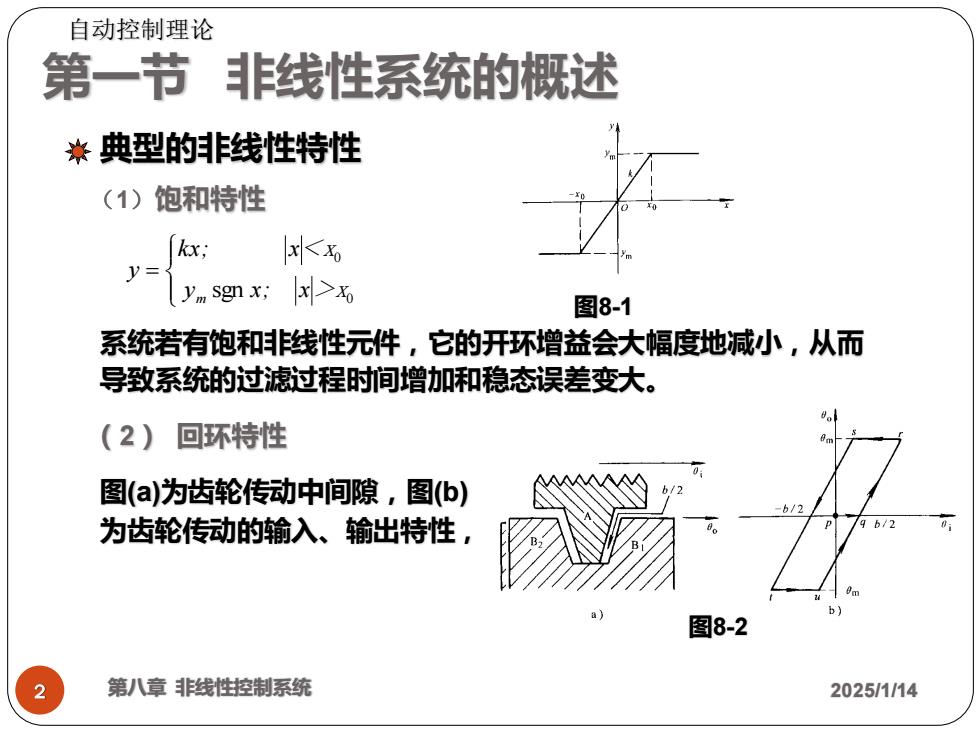
自动控制理论 第一节非线性系统的概述 米典型的非线性特性 (1)饱和特性 kx; 长6 y y sgn x; x>x 图8-1 系统若有饱和非线性元件，它的开环增益会大幅度地减小，从而 导致系统的过滤过程时间增加和稳态误差变大。 (2)回环特性 图(a)为齿轮传动中间隙，图(b) 为齿轮传动的输入、输出特性， b/1 图8-2 2 第八章非线性控制系统 2025/1/14

第一节 非线性系统的概述 2 第八章 非线性控制系统 2025/1/14 典型的非线性特性 （1）饱和特性     = y x; x＞x kx; x＜x y m 0 0 sgn 系统若有饱和非线性元件，它的开环增益会大幅度地减小，从而 导致系统的过滤过程时间增加和稳态误差变大。 （2） 回环特性 图8-1 图8-2 图(a)为齿轮传动中间隙，图(b) 为齿轮传动的输入、输出特性， 自动控制理论

自动控制理论 它的数学表达式为 0,-5 0>0 0。= 阳，+分 8<0 0msgn0。; 0=0 b-齿轮间隙 1)回环非线性特性是多值的，对于一个给定的输入，究竟取那一个值作为 输出，应视该输入的“历史”决定。 2)系统中若有回环非线性元件存在，通常会使系统的输出在相位上产生滞 后，从而导致系统稳定量的减小、动态性能的恶化，甚至使系统产生自持振 荡。 (3)死区特性 0 A y= k(x-4sgn x) 图8-3 3 第八章非线性控制系统 2025/1/14

3 第八章 非线性控制系统 2025/1/14 它的数学表达式为 ( ) ( ) − − −齿轮间隙        = + − = b θ θ ; θ k θ b ; θ＜ k θ b ; θ＞ θ m i i sgn 0 0 2 0 2 0 0    1）回环非线性特性是多值的，对于一个给定的输入，究竟取那一个值作为 输出，应视该输入的“历史”决定。 2）系统中若有回环非线性元件存在，通常会使系统的输出在相位上产生滞 后，从而导致系统稳定量的减小、动态性能的恶化，甚至使系统产生自持振 荡。 （3）死区特性 ( )    = k x -Δ x x＞Δ x＜Δ y sgn 0 图8-3 自动控制理论

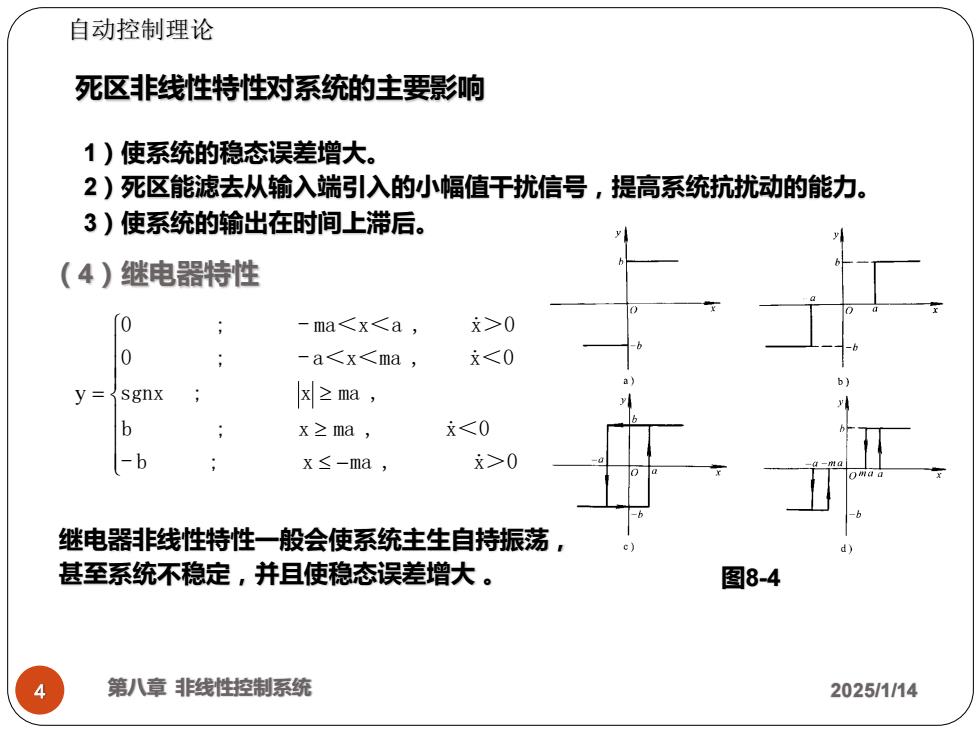
自动控制理论 死区非线性特性对系统的主要影响 1)使系统的稳态误差增大。 2)死区能滤去从输入端引入的小幅值干扰信号，提高系统抗扰动的能力。 3)使系统的输出在时间上滞后。 (4)继电器特性 0 -ma0 0 -a0 继电器非线性特性一般会使系统主生自持振荡， 甚至系统不稳定，并且使稳态误差增大。 图8-4 第八章非线性控制系统 2025/1/14

4 第八章 非线性控制系统 2025/1/14 1）使系统的稳态误差增大。 2）死区能滤去从输入端引入的小幅值干扰信号，提高系统抗扰动的能力。 3）使系统的输出在时间上滞后。 死区非线性特性对系统的主要影响 （4）继电器特性 图8-4           −  =  - b ; x ma , x＞0 b ; x ma , x＜0 sgnx ; x ma , 0 ; - a＜x＜ma , x＜0 0 ; - ma＜x＜a , x＞0     y 继电器非线性特性一般会使系统主生自持振荡， 甚至系统不稳定，并且使稳态误差增大 。 自动控制理论

自动控制理论 嶚非线性系统的特点 1)非线性系统的输出与输入间不存在着比例关系，且不适用叠加原理 2)非线性系统的稳定性不仅与系统的结构和参数有关，而且也与初始 条件和输入信号的大小有关。 下面举例说明初始偏差对系统稳定性影响 设非线性系统的微分方程为 +1-x)x=0 当初始偏差X0,方程具有负实根，相应的系统是稳定的 当x0>1时，1-X<0,方程具有一个正的实根，系统为不稳定 非线性系统常会产生自持振荡 研究非线性系统的方法： 1)描述函数法-一用于研究系统的稳定性和自持振 荡问题。 2)相平面法-只适用于一阶和二阶系统。 3)李雅普诺夫第二法。 图8-5 5 第八章非线性控制系统 2025/1/14

5 第八章 非线性控制系统 2025/1/14 x  +(1− x)x = 0 非线性系统的特点 1）非线性系统的输出与输入间不存在着比例关系,且不适用叠加原理。 2）非线性系统.的稳定性不仅与系统的结构和参数有关,而且也与初始 条件和输入信号的大小有关。 下面举例说明初始偏差对系统稳定性影响 设非线性系统的微分方程为 当初始偏差 x00,方程具有负实根,相应的系统是稳定的 当x0>1时,1-x0<0,方程具有一个正的实根,系统为不稳定 图8-5 非线性系统常会产生自持振荡 1）描述函数法-用于研究系统的稳定性和自持振 荡问题。 2）相平面法-只适用于一阶和二阶系统。 3）李雅普诺夫第二法。 研究非线性系统的方法: 自动控制理论

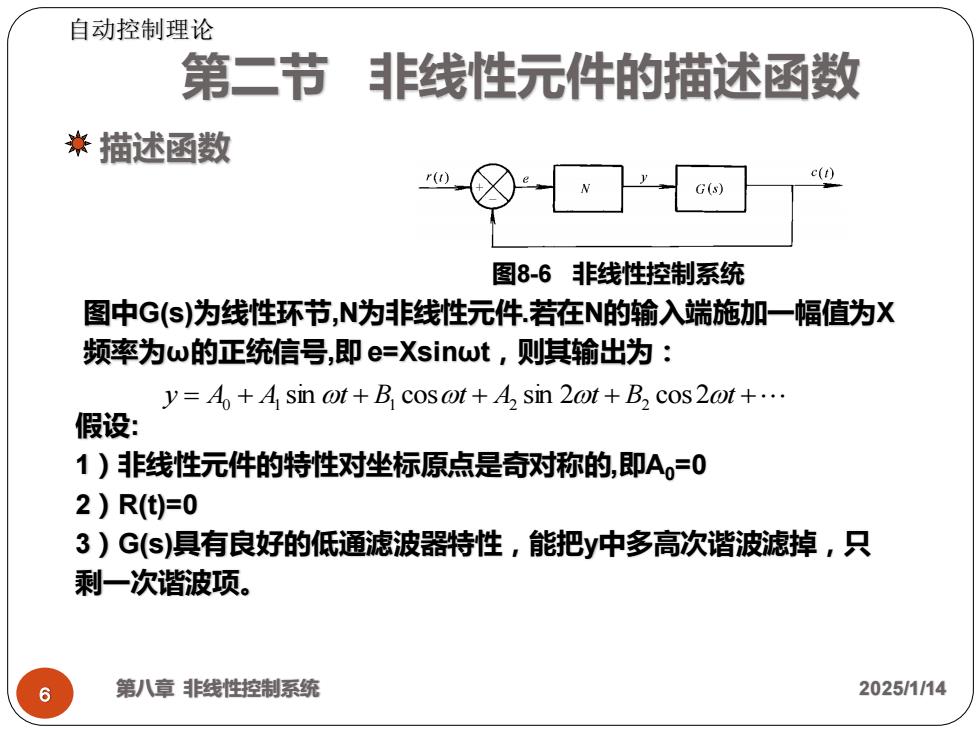
自动控制理论 第二节 非线性元件的描述函数 米描述函数 r(0 e(t) G( 图8-6非线性控制系统 图中G(S)为线性环节，为非线性元件.若在N的输入端施加一幅值为X 频率为w的正统信号，即e=Xsinwt,则其输出为： y=A+4 sin ot+B cosot+4 sin 2ot+B2 cos2ot+. 假设： 1)非线性元件的特性对坐标原点是奇对称的，即A,=0 2)R()=0 3)G(s)具有良好的低通滤波器特性，能把y中多高次谐波滤掉，只 剩一次谐波项。 第八章非线性控制系统 2025/1/14

y = A0 + A1 sin t + B1 cost + A2 sin 2t + B2 cos2t + 第八章 非线性控制系统 2025/1/14 6 描述函数 图8-6 非线性控制系统 图中G(s)为线性环节,N为非线性元件.若在N的输入端施加一幅值为X 频率为ω的正统信号,即 e=Xsinωt，则其输出为： 第二节 非线性元件的描述函数 假设: 1）非线性元件的特性对坐标原点是奇对称的,即A0=0 2）R(t)=0 3）G(s)具有良好的低通滤波器特性，能把y中多高次谐波滤掉，只 剩一次谐波项。 自动控制理论

自动控制理论 则 Jy=A sin ot-+B,cos@t=Ysin(ot+Φ，) 其中 ==arctan ysiawtd(ot)） B= ycosotd(ot) 经过线性化处理后，非线性元件的输出是一个与其输入信号同频率的 正弦函数，仅在幅值和相位上与输入信号有差异。 非线性特性线性化的条件： 1)假设系统的输入)=0 2)非线性元件的静特性不是时间t的函数 3)非线性元件的特性是奇对称的，即有 f(e)=-f(-e) 第八章非线性控制系统 2025/1/14

( ) 1 1 1 1 y = A sint + B cost =Y sin t + ( ) B y td( t) A ysia td t A B Y A B          cos 1 1 , arctan 2 0 1 2 0 1 1 1 1 2 1 2 1 1   = = = + = 第八章 非线性控制系统 2025/1/14 7 则 其中 经过线性化处理后，非线性元件的输出是一个与其输入信号同频率的 正弦函数，仅在幅值和相位上与输入信号有差异。 非线性特性线性化的条件： 1）假设系统的输入r(t)=0 2）非线性元件的静特性不是时间t的函数 3）非线性元件的特性是奇对称的，即有 f (e)= − f (−e) 1 1 自动控制理论

自动控制理论 4)系统的线性部分具有良好低通滤波器的性能，经过线性化后，非线性元 件的输出与输入的关系为 : (arctan N(X)-非线性特性的描述函数 r() c() N(X) G(j) 图8-7用描述函数表示非线性特性的系统 *非线性元件函数的举例 (1)饱和非线性 由图8-8可知，输出y()是一个周期性的奇函数，因而它的傅氏级数展开式 中没有直流项，也没有余弦项。即A=0,B=0,日1=0 y (t)=Ysin ot =A sin ot 式中4=4 ysinotd(ot) 4kX sin otsin oid(ot)+kSsin ofd(o) 8 第八章非线性控制系统 2025/1/14

8 第八章 非线性控制系统 2025/1/14 ( ) 1 1 2 1 2 1 1 1 arctan A B X A B X Y N X  + =  = 4）系统的线性部分具有良好低通滤波器的性能 ，经过线性化后，非线性元 件的输出与输入的关系为 ： N(X)-非线性特性的描述函数 图8-7 用描述函数表示非线性特性的系统 非线性元件函数的举例 （1）饱和非线性 由图8-8可知，输出y(t)是一个周期性的奇函数，因而它的傅氏级数展开式 中没有直流项，也没有余弦项。即 A0=0，B1=0，θ1=0 自动控制理论 ( ) A y td( t) y t Y t A t        = = = 2 0 1 1 1 sin 4 sin sin 式中 k X t td(t) k S td(t)     sin sin sin 4 2 0  = +

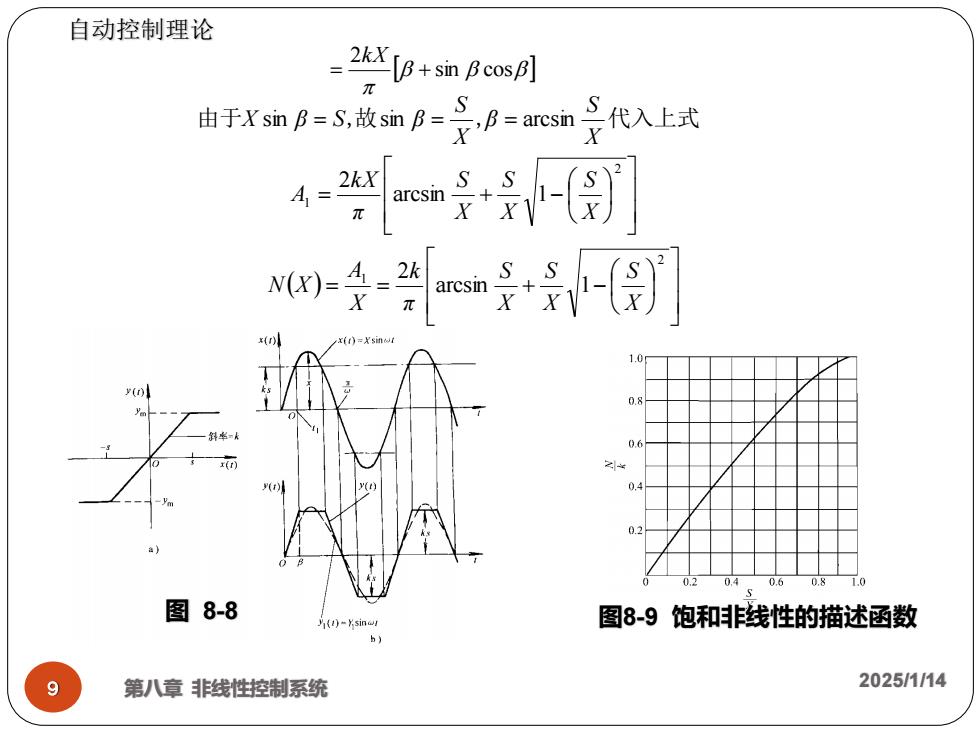
自动控制理论 -2兴p:Bcm 由于XsmB=S故smB=S,B=arcsin代入上式 4 00-m+-气 x( y() 0.4 0.6 0.8 1.0 图8-8 ()-Ysin 图89饱和非线性的描述函数 9 第八章非线性控制系统 2025/1/14

( )               = = + −               = + − = = = 2 1 2 1 arcsin 1 2 arcsin 1 2 sin sin arcsin X S X S X S π k X A N X X S X S X S π k X A X S β X S X β S β 由于 ,故 , 代入上式 第八章 非线性控制系统 2025/1/14 9 图8-9 饱和非线性的描述函数 自动控制理论 图 8-8      sin cos 2 = + k X

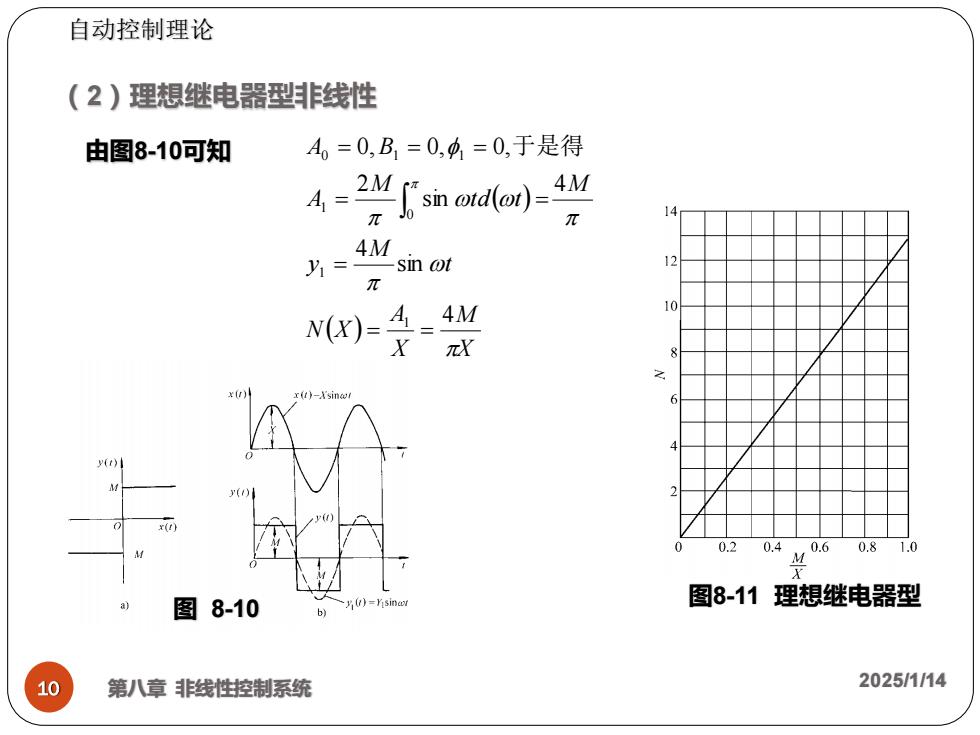
自动控制理论 (2)理想继电器型非线性 由图8-10可知 A0=0,B1=0,中，=0，于是得 2 sn od(o）)-4 4 4M y1= sin ot π N(X)=4=4M 10 XπX t)-sing it) 0 0.20.4.0.60.81.0 M 图8-10 y(1)=Yisinar 图8-11理想继电器型 10 第八章非线性控制系统 2025/1114

( ) ( ) X M X A N X t M y M td t M A A B          4 sin 4 4 sin 2 0, 0, 0, 1 1 0 1 0 1 1 = = = = = = = =  于是得 第八章 非线性控制系统 2025/1/14 10 （2）理想继电器型非线性 图 8-10 由图8-10可知 图8-11 理想继电器型 自动控制理论