
第八章非线性控制系统 前面各章阐述了线性定常系统的分析与综合。严格来说,理想的线性系统是不 存在的,总会有一些非线性因素。前面各章的系统是进行线性化处理后近似当作线 性系统来研究的,从而可以用线性控制理论对系统进行分析和研究。但是,并不是 所有的非线性系统都可以进行线性化处理,对于某些不能进行线性化处理的系统, 称为本质非线性控制系统。非线性控制系统与线性控制系统最重要的区别在于非线 性控制系统不满足叠加原理,且系统的响应与初始状态有关。因此,前面各章用于 分析线性控制系统的有效方法,不能直接用于非线性控制系统。到目前为止,对非 线性控制系统的分析研究,没有一种象线性控制系统那样普遍适用的方法。已有的 方法,在应用上都有一定的局限性。所以对某类非线性控制系统,必须考虑相应的 分析和设计方法。 8.1非线性控制系统概述 实际控制系统中,非线性特性有很多类型,下面只介绍几种常见典型非线性特 性。 一、典型的非线性特性 1.饱和特性 图&-1是饱和非线性的静特性。图中ε()为非线性环节的输入信号,x()为非 线性环节的输出信号。其数学表达式为 0= Ke(t) le)≤a Ka·signe() e(t)>a (81) 式中,K为线性区的斜率,a为线性区的宽度,signe()为开关函数。 对于饱和非线性特性,当输入信号©()超出线性范用后,输出信号x不再随输 入©()的增大而变化,且被限制于某恒定值b(称为饱和值),而b=Ka。 饱和非线性可以由磁饱和、放大器输出饱和、功率限制等引起。一般情况下 系统因存在饱和特性的元件,当输入信号超过线性区时,系统的开环增益会有大幅 度地减小,从而导致系统过渡过程时间的增加和稳态误差的加大。但在某些自动控 制系统中饱和特性能够起到抑制系统振荡的作用。因为在暂态过程中,当偏差信号 增大进入饱和区时,系统的开环放大系数下降,从而抑制了系统振荡。在自动调速 系统中,常人为地引入饱和特性,以限制电动机的最大电流。 x(t) x(t) K K r) e(t) a 图81饱和特性 图8-2 死区特性 117
117 第八章 非线性控制系统 前面各章阐述了线性定常系统的分析与综合。严格来说,理想的线性系统是不 存在的,总会有一些非线性因素。前面各章的系统是进行线性化处理后近似当作线 性系统来研究的,从而可以用线性控制理论对系统进行分析和研究。但是,并不是 所有的非线性系统都可以进行线性化处理,对于某些不能进行线性化处理的系统, 称为本质非线性控制系统。非线性控制系统与线性控制系统最重要的区别在于非线 性控制系统不满足叠加原理,且系统的响应与初始状态有关。因此,前面各章用于 分析线性控制系统的有效方法,不能直接用于非线性控制系统。到目前为止,对非 线性控制系统的分析研究,没有一种象线性控制系统那样普遍适用的方法。已有的 方法,在应用上都有一定的局限性。所以对某类非线性控制系统,必须考虑相应的 分析和设计方法。 8.1 非线性控制系统概述 实际控制系统中,非线性特性有很多类型,下面只介绍几种常见典型非线性特 性。 一、典型的非线性特性 1.饱和特性 图 8-1 是饱和非线性的静特性。图中 e (t)为非线性环节的输入信号,x (t) 为非 线性环节的输出信号。其数学表达式为 = Ka signe t e t a Ke t e t a ( ) ( ) ( ) ( ) x(t) 式中,K 为线性区的斜率, a 为线性区的宽度,signe (t)为开关函数。 对于饱和非线性特性,当输入信号 e (t)超出线性范围后,输出信号 x 不再随输 入 e (t)的增大而变化,且被限制于某恒定值 b(称为饱和值),而 b=K a 。 饱和非线性可以由磁饱和、放大器输出饱和、功率限制等引起。一般情况下, 系统因存在饱和特性的元件,当输入信号超过线性区时,系统的开环增益会有大幅 度地减小,从而导致系统过渡过程时间的增加和稳态误差的加大。但在某些自动控 制系统中饱和特性能够起到抑制系统振荡的作用。因为在暂态过程中,当偏差信号 增大进入饱和区时,系统的开环放大系数下降,从而抑制了系统振荡。在自动调速 系统中,常人为地引入饱和特性,以限制电动机的最大电流。 图 8-1 饱和特性 图 8-2 死区特性 a a x(t) x(t) b - a K e(t) 0 - a K e(t) (8-1)

2.死区特性 图8-2是死区非线性特性。其数学表达式为 0 le(t)≤a x0= K[e(t)-a·signe(t] e(t)>a (8-2) 式中,a为死区宽度,K为死区的斜率。 该特性表现在|e()|≤a范围内,当输入e)变化时,输出x无反应。这一范 围称为死区(或称为不灵敏区)。当输入c()超出死区范围,即|e(0|>a时,输出 x与输入e()成比例变化。 死风特性常见于测量、放大或传动蕴合部件的间隙中。该特性的存在对系统喜 生的影响有:(1)降低了系统的稳态准确度,使稳态误差不可能小于死区值。(2) 对系统暂态性能影响的利弊与系统的结构和参数有关,如某些系统,由于死区特性 的存在,可以抑制系统的振荡:而对另一些系统,死区又能导致系统产生自振荡。 (3)死区能滤去从输入引入的小幅值干扰信号,提高系统抗干扰能力。一些场合, 为提高系统的抗干扰能力,有时要故意引入或增大死区。(4)由于死区存在有时会 引起系统在输出端的滞后。 3.回环特性 回环特性又称为环(间隙)特性。该特性如图8-3(a)所示。其数学表达式为 K[e(t)-a] e)>0 x)=Ke()+a可 e()<0 (8-3) b·signe(t) e(t)=0 式中,a为间隙宽度,K为输出特性的斜率,b为常数。 当输入c()增大并超过a之后,输出x)与输入c(0成比例,随着输入量的增大 输出量沿特性①上升。当输入增大到某值后开始减小时,输出量则保持不变,直至 输入量减小了2a之后,输出量方沿特性②下降。 机械传动中的齿轮间隙是典型的回环特性。图8-3(b)表示具有这种特性的传 动装置。 回环特性的存在,会使系统稳态误差增大,相位滞后增大,系统暂态特性变坏, 甚至使系统不稳定或产生自振荡,因此应消除或减弱它的影响。 x( 2q e(t) e(t) 给入 图8-3回环特性 118
118 2.死区特性 图 8-2 是死区非线性特性。其数学表达式为 − = K e t a signe t e t a e t a [ ( ) ( )] ( ) 0 ( ) x(t) 式中, a 为死区宽度,K 为死区的斜率。 该特性表现在│e (t)│≤ a 范围内,当输入 e (t)变化时,输出 x 无反应。这一范 围称为死区(或称为不灵敏区)。当输入 e (t)超出死区范围,即│e (t)│> a 时,输出 x 与输入 e (t)成比例变化。 死区特性常见于测量、放大或传动藕合部件的间隙中。该特性的存在对系统产 生的影响有:(1)降低了系统的稳态准确度,使稳态误差不可能小于死区值。(2) 对系统暂态性能影响的利弊与系统的结构和参数有关,如某些系统,由于死区特性 的存在,可以抑制系统的振荡;而对另一些系统,死区又能导致系统产生自振荡。 (3)死区能滤去从输入引入的小幅值干扰信号,提高系统抗干扰能力。一些场合, 为提高系统的抗干扰能力,有时要故意引入或增大死区。(4)由于死区存在有时会 引起系统在输出端的滞后。 3.回环特性 回环特性又称为环(间隙)特性。该特性如图 8-3( a )所示。其数学表达式为 = + − = ( ) 0 ( ) 0 ( ) [ ( ) ] [ ( ) ] ( ) 0 x(t) . . . e t e t b signe t K e t a K e t a e t 式中, a 为间隙宽度,K 为输出特性的斜率,b 为常数。 当输入 e(t)增大并超过 a 之后,输出 x(t)与输入 e(t)成比例,随着输入量的增大 输出量沿特性①上升。当输入增大到某值后开始减小时,输出量则保持不变,直至 输入量减小了 2 a 之后,输出量方沿特性②下降。 机械传动中的齿轮间隙是典型的回环特性。图 8-3(b)表示具有这种特性的传 动装置。 回环特性的存在,会使系统稳态误差增大,相位滞后增大,系统暂态特性变坏, 甚至使系统不稳定或产生自振荡,因此应消除或减弱它的影响。 ( a ) (b) 图 8-3 回环特性 a a - a a ② b ① 0 e(t) 1 x(t) 输出部件 输入部件 x (t) 2 a e (t) (8-2) (8-3)

4.继电器特性 x() |x(o) 6 ma e(t) o ma b -b (b) x(t) e(t) c(t) 0 a 6 图8-4继电器特性 图84给出了几种型式的继电器特性。其中图8-4(a)是兼有死区和回环的继 电器特性,。图8-4(b)是理想继电器特性,当吸合电压值a和释放电压值ma很小 时,可视为这种特性。当吸合电压值与释放电压值相同时,则图8-4(©)所示的列 区继电器特性。图8-4()是回环继电器特性,该特性的特点是,反向释放电压与 正向吸合电压相同,以及正向释放电压与反向吸合电压相同。 般继电器总有一定 的吸合电压值,所以特性必然出现死区和回环,所以,实际的非线性继电特性如图 8-4(a)。其数学表达式为 -ma0 0 -a0 式中,a为吸合电压值,ma为释放电压值,b为继电器的饱和输出 继电器非线性特性一般会使系统产生自振荡,甚至导致系统不稳定,并且也使 其稳态误差增大。但继电特性能够使被控制的执行电机始终工作在额定或最大电压 下,可以充分发挥其调节能力,实现快速控制。 5.变放大系数特性 119
119 4.继电器特性 ( a ) (b) (c) (d) 图 8-4 继电器特性 图 8-4 给出了几种型式的继电器特性。其中图 8-4( a )是兼有死区和回环的继 电器特性,。图 8-4(b)是理想继电器特性,当吸合电压值 a 和释放电压值 m a 很小 时,可视为这种特性。当吸合电压值与释放电压值相同时,则图 8-4(c)所示的死 区继电器特性。图 8-4(d)是回环继电器特性,该特性的特点是,反向释放电压与 正向吸合电压相同,以及正向释放电压与反向吸合电压相同。一般继电器总有一定 的吸合电压值,所以特性必然出现死区和回环,所以,实际的非线性继电特性如图 8-4( a )。其数学表达式为 − − − − = • • • • ( ) , ( ) 0 ( ) , ( ) 0 . ( ) ( ) 0 ( ) , ( ) 0 0 ( ) , ( ) 0 ( ) b e t ma e t b e t ma e t b signe t e t a a e t ma e t ma e t a e t x t 式中, a 为吸合电压值,m a 为释放电压值,b 为继电器的饱和输出。 继电器非线性特性一般会使系统产生自振荡,甚至导致系统不稳定,并且也使 其稳态误差增大。但继电特性能够使被控制的执行电机始终工作在额定或最大电压 下,可以充分发挥其调节能力,实现快速控制。 5.变放大系数特性 - a a - a a - a a -m a e(t) x (t) x (t) e(t) x (t) e(t) 0 0 0 0 -b - b - b m a b b e(t) x (t) b (8-4)

变放大系数特性如图8-5所示。其数学表达式 K,e() x()= le(t≤a K2e(t) e(t)>a (8-5) 式中K、K,为输出特性的斜率,a为切换点。 该特性表示,当输入信号幅值不同时,元件的 放大系数也不同。从而使系统在大误差时具有较大 的放大系数,系统的响应迅速:而在小误差时,系 图85变放大系数特性 统具有较小的放大系数,从而系统的响应缓而稳。具有该非线性的系统,其动态品 质较好。 二、非线性系统的特性 非线性元件系统与线性控制系统相比,有如下特点: 1.叠加原理不适用于非线性控制系统。即几个输入信号作用于非线性控制系统 所引起的输出,不再等于每一个输入信号所引起的输出之总和。 2.在线性控制系统中,当输入是正弦信号时,则输出为同频率的正弦信号。 在非线性控制系统中,如果输入是正弦信号,输出就不一定是正弦信号,而是一个 畸变的波形,它可以分解为正弦波和无穷多谐波的叠加。 3.线性控制系统的稳定性,只与系统的结构和参数有关,而与系统输入无关。 非线性控制系统的稳定性,不仅取决于系统的结构和参数,而且与输入信号的幅值 和初始条件有关。对于同一结构和参数的非线性控制系统,在不同的初态下,运动 的最终状态可以完全不同。如当初态(x。,x。)处于较小区域时,(x,x)>0,系统 是稳定的:而(x,x)处于较大区域时,S(x,x)≤0,系统则变得不稳定,甚至还 可能变为更复杂的情况。总之,等效阻尼比5随(x,x)的变化情况决定着非线性系 统的全部动态过程。 4.非线性控制系统常常产生自振荡。线性系统只有两种基本的暂态响应模式: 收敛和发散。当系统处于稳定的临界状态时,才会产生等幅振荡。然而,线性系统 的等幅振荡是暂时性的,只要系统中的参数稍有微小的变化,系统就有临界稳定状 态趋于发散或收敛。但在非线性控制系统中,即使没有外加的输入信号,系统自身 产生一个有一定频率和幅值的稳定振荡,称为自振荡(自持振荡)。自振荡是非线性 控制系统的特有运动模式,它的振幅和频率由系统本身的特性所决定。 三、非线性控制系统的分析研究方法 由于非线性控制系统与线性控制系统有很大的差异,因此,不能直接用前面介 绍的线性理论去分析它,否则会导致错误的结论。对非线性控制系统的分析,还没 有一种象线性控制系统那么普遍的分析、设计方法。目前分析非线性控制系统的常 120
120 变放大系数特性如图 8-5 所示。其数学表达式 为 = K e t e t a K e t e t a x t ( ) ( ) ( ) ( ) ( ) 2 1 式中 K1、 K2 为输出特性的斜率, a 为切换点。 该特性表示,当输入信号幅值不同时,元件的 放大系数也不同。从而使系统在大误差时具有较大 的放大系数,系统的响应迅速;而在小误差时,系 图 8-5 变放大系数特性 统具有较小的放大系数,从而系统的响应缓而稳。具有该非线性的系统,其动态品 质较好。 二、非线性系统的特性 非线性元件系统与线性控制系统相比,有如下特点: 1.叠加原理不适用于非线性控制系统。即几个输入信号作用于非线性控制系统 所引起的输出,不再等于每一个输入信号所引起的输出之总和。 2. 在线性控制系统中,当输入是正弦信号时,则输出为同频率的正弦信号。 在非线性控制系统中,如果输入是正弦信号,输出就不一定是正弦信号,而是一个 畸变的波形,它可以分解为正弦波和无穷多谐波的叠加。 3.线性控制系统的稳定性,只与系统的结构和参数有关,而与系统输入无关。 非线性控制系统的稳定性,不仅取决于系统的结构和参数,而且与输入信号的幅值 和初始条件有关。对于同一结构和参数的非线性控制系统,在不同的初态下,运动 的最终状态可以完全不同。如当初态 ( , ) 0 0 x x • 处于较小区域时, ( , ) 0 • x x ,系统 是稳定的;而 ( , ) 0 0 x x • 处于较大区域时, ( , ) 0 • x x ,系统则变得不稳定,甚至还 可能变为更复杂的情况。总之,等效阻尼比 随 (x, x) • 的变化情况决定着非线性系 统的全部动态过程。 4.非线性控制系统常常产生自振荡。线性系统只有两种基本的暂态响应模式: 收敛和发散。当系统处于稳定的临界状态时,才会产生等幅振荡。然而,线性系统 的等幅振荡是暂时性的,只要系统中的参数稍有微小的变化,系统就有临界稳定状 态趋于发散或收敛。但在非线性控制系统中,即使没有外加的输入信号,系统自身 产生一个有一定频率和幅值的稳定振荡,称为自振荡(自持振荡)。自振荡是非线性 控制系统的特有运动模式,它的振幅和频率由系统本身的特性所决定。 三、非线性控制系统的分析研究方法 由于非线性控制系统与线性控制系统有很大的差异,因此,不能直接用前面介 绍的线性理论去分析它,否则会导致错误的结论。对非线性控制系统的分析,还没 有一种象线性控制系统那么普遍的分析、设计方法。目前分析非线性控制系统的常 1 k x (t) e(t) 0 a - a (8-5) 2 k

用方法有如下三种: 1.描述函数法 一种基于频率域的分析方法。在一定的条件下,用非线性元件 输出的基波信号代替在正弦作用下的非正弦输出,使非线性元件近似于一个线性元 件,从而可以应用乃奎斯特稳定判据对系统的稳定性进行判别。这种方法主要用于 研究非线性系统的稳定性和自振荡问题。如系统产生自振荡,如何求出其振荡的频 率和幅值,以及寻求消除自振荡的方法等。 2.相平面法一种基于时域的分析方法。根据绘制出的文一X相轨迹图,去研 究非线性系统的稳定性和动态性能。这种方法只适用于一、二阶系统。 3.李雅普诺夫第二法这是一种对线性系统和非线性系统都适用的方法。根 据非线性系统动态方程的特征,用相关的方法求出李雅普诺夫函数V(x),然后根据 V(x)和广(x)的性质去判别非线性系统的稳定性。 4.这些方法都有一定的局限性。如相平面法,是一种图解法,能给出稳态和 暂态性能的全部信息,但只适用于一、二阶非线性控制系统。描述函数法是一种近 似的线性方法,虽不受阶次的限制,但只能给出系统的稳定性和自振荡的信息。尽 管如此,它们仍不失为目前分析非线性控制系统有效方法,故得到广泛应用,本章 只介绍描述函数法。 8.2描述函数法 描述函数法是一种近似的线性化方法,它应用了线性理论中频率法的某些结论 和方法,是频率法在非线性控制系统中的扩展。 8.2.1描述函数法的基本思想 设非线性控制系统经过变换和归化可表示为图8-6所示的典型结构。其中N是 非雄M=件,G(S)为系统的线性环节。 c(t) NGC) e)N 30) 图8-6非线性控制系统典型结构图 图8-7非线性元件 我们知道,线性元件在正弦信号输入时,其输出也是同频率的正弦函数,可以 用幅相频率特性来描述。但是对于非线性元件,当输入为正弦信号时,即 e(t)=Asin1,其输出x(t)一般为同频率的非正弦周期函数,即输出不仅含有与 输入同频率的基波分量,而且还含有高次谐波分量。故非线性元件不能直接用幅相 频率特性来描述。 描述函数法的基本思想是将非线性元件输出中的基波分量代替实际的非正弦周 期信号,而略去信号中的高次谐波。这样处理后,就与线性元件在正弦信号信用下 的输出具有形式上的相似,可以仿照幅相频率特性的定义,建立非线性元件的近似 121
121 用方法有如下三种: 1. 描述函数法 一种基于频率域的分析方法。在一定的条件下,用非线性元件 输出的基波信号代替在正弦作用下的非正弦输出,使非线性元件近似于一个线性元 件,从而可以应用乃奎斯特稳定判据对系统的稳定性进行判别。这种方法主要用于 研究非线性系统的稳定性和自振荡问题。如系统产生自振荡,如何求出其振荡的频 率和幅值,以及寻求消除自振荡的方法等。 2. 相平面法 一种基于时域的分析方法。根据绘制出的 x − x 相轨迹图,去研 究非线性系统的稳定性和动态性能。这种方法只适用于一、二阶系统。 3. 李雅普诺夫第二法 这是一种对线性系统和非线性系统都适用的方法。根 据非线性系统动态方程的特征,用相关的方法求出李雅普诺夫函数 V(x),然后根据 V(x)和 V (x) 的性质去判别非线性系统的稳定性。 4. 这些方法都有一定的局限性。如相平面法,是一种图解法,能给出稳态和 暂态性能的全部信息,但只适用于一、二阶非线性控制系统。描述函数法是一种近 似的线性方法,虽不受阶次的限制,但只能给出系统的稳定性和自振荡的信息。尽 管如此,它们仍不失为目前分析非线性控制系统有效方法,故得到广泛应用,本章 只介绍描述函数法。 8.2 描述函数法 描述函数法是一种近似的线性化方法,它应用了线性理论中频率法的某些结论 和方法,是频率法在非线性控制系统中的扩展。 8.2.1 描述函数法的基本思想 设非线性控制系统经过变换和归化可表示为图 8-6 所示的典型结构。其中 N 是 非线性元件, G(s) 为系统的线性环节。 图 8-6 非线性控制系统典型结构图 图 8-7 非线性元件 我们知道,线性元件在正弦信号输入时,其输出也是同频率的正弦函数,可以 用幅相频率特性来描述。但是对于非线性元件,当输入为正弦信号时,即 e(t) = Asin t ,其输出 x(t) 一般为同频率的非正弦周期函数,即输出不仅含有与 输入同频率的基波分量,而且还含有高次谐波分量。故非线性元件不能直接用幅相 频率特性来描述。 描述函数法的基本思想是将非线性元件输出中的基波分量代替实际的非正弦周 期信号,而略去信号中的高次谐波。这样处理后,就与线性元件在正弦信号信用下 的输出具有形式上的相似,可以仿照幅相频率特性的定义,建立非线性元件的近似 e(t) x(t) c(t) r(t) — — G(s) N N

幅相特性,即描述函数。为此要求非线性控制系统满足以下条件: 1.非线性元件N无惯性。 2.非线性元件N的特性是斜对称的,即f(e)=-f(-e)。因此在正弦信号作用 下,输出量的平均值等于零,没有恒定直流分量。前节所例举的典型非线性元件均 满足以上二个条件。 3.系统中的线性部份G(s)具有良好的低通滤波特性。这个条件对一般控制系 统来说是可以满足的,而且线性部份阶次越高,低通滤波特性越好。这一点使得非 线性元件输出量中的高次谐波通过线性部份后,其幅值被衰减的很小,近似认为只 有基波沿着闭环通道传递。显然这种近似的准确性完全取决于非线性元件输出信号 中高次谐波相对于基波成份的比例,高次谐波成份比例小,准确性高,反之,误差 较大。 8.2.2描球函数法的表示式 根据以上的基本思想和应用条件,可推导出非线性元件的数学模型一描述函数。 图&-7所示的非线性元件,假设它的输出量x()只与输入量(t)有关,即 x=f(e) 当输入量为正弦函数e()=Asin o1时,其输出x(t)一般是非正弦周期函数。 将输出x()用富氏级数展开,可以写成 ()(d cos Kor +B sin) (8-6) 考虑到非线性控制系统满足上述应用条件,则级数中的恒定分量A=O,高次谐 波可忽略。故式(8-6)可简化为 x(1)=A coso+B sin ax =Ci sindox+)(8-7) 式中 ',()(or) B ()sin ond(cox) C=42+B2 一基波分量的幅值 122
122 (8-6) 幅相特性,即描述函数。为此要求非线性控制系统满足以下条件: 1. 非线性元件 N 无惯性。 2. 非线性元件 N 的特性是斜对称的,即 f (e) = − f (−e) 。因此在正弦信号作用 下,输出量的平均值等于零,没有恒定直流分量。前节所例举的典型非线性元件均 满足以上二个条件。 3. 系统中的线性部份 G(s) 具有良好的低通滤波特性。这个条件对一般控制系 统来说是可以满足的,而且线性部份阶次越高,低通滤波特性越好。这一点使得非 线性元件输出量中的高次谐波通过线性部份后,其幅值被衰减的很小,近似认为只 有基波沿着闭环通道传递。显然这种近似的准确性完全取决于非线性元件输出信号 中高次谐波相对于基波成份的比例,高次谐波成份比例小,准确性高,反之,误差 较大。 8.2.2 描述函数法的表示式 根据以上的基本思想和应用条件,可推导出非线性元件的数学模型—描述函数。 图 8-7 所示的非线性元件,假设它的输出量 x(t) 只与输入量 e(t) 有关,即 x = f (e) 当输入量为正弦函数 e(t) = Asin t 时,其输出 x(t) 一般是非正弦周期函数。 将输出 x(t) 用富氏级数展开,可以写成 = = + + 0 0 ( ) ( cos sin ) k K k x t A A Kt B Kt 考虑到非线性控制系统满足上述应用条件,则级数中的恒定分量 A0=0,高次谐 波可忽略。故式(8-6)可简化为 ( ) cos sin sin( ) = 1 + 1 = 1 +1 x t A t B t C t 式中 ( ) cos ( ) 1 2 0 1 2 A x t td t = ( )sin ( ) 1 2 0 1 2 B x t td t = 2 1 2 C1 = A1 + B -基波分量的幅值 (8-7)
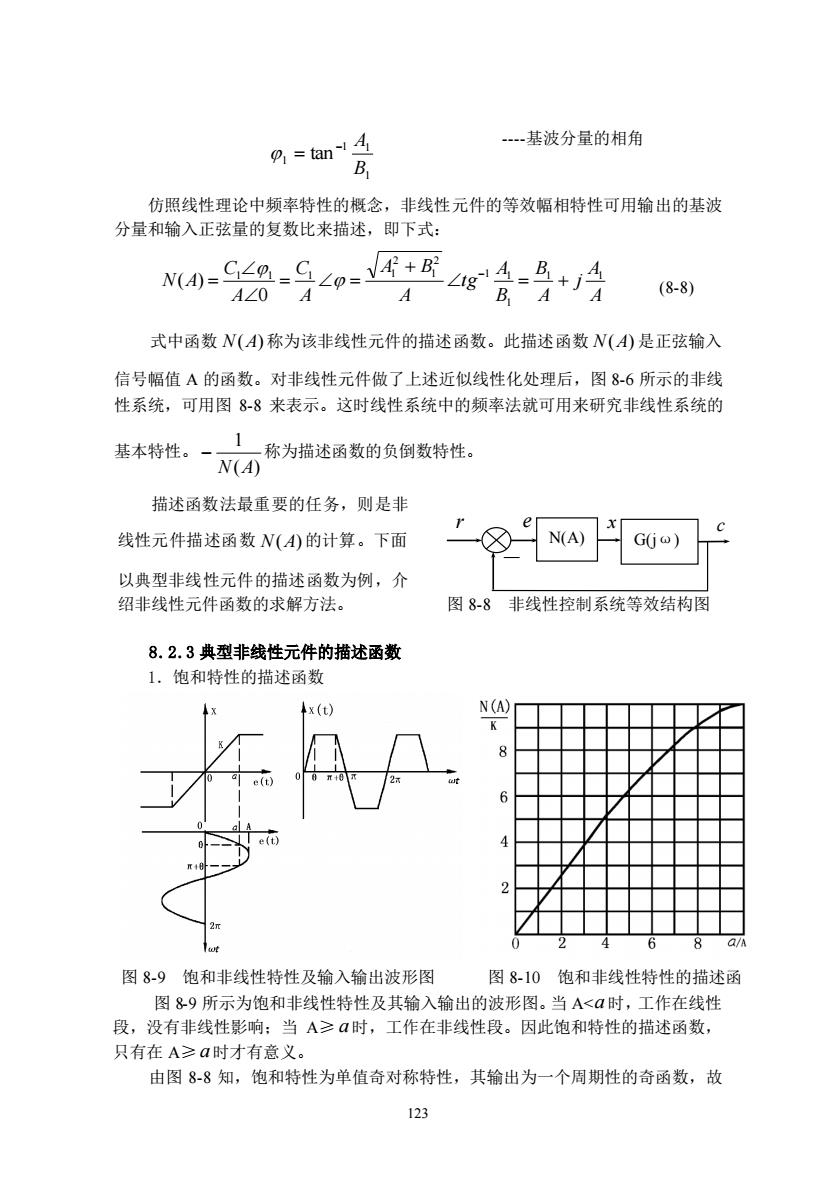
9=tan 基波分量的相角 B 仿照线性理论中频率特性的概念,非线性元件的等效幅相特性可用输出的基波 分量和输入正弦量的复数比来描述,即下式: N0=Sg-S∠0=V霄+R A∠0A A B A (8-8) 式中函数N(A)称为该非线性元件的描述函数。此描述函数N(A)是正弦输入 信号幅值A的函数。对非线性元件做了上述近似线性化处理后,图86所示的非线 性系统,可用图88来表示。这时线性系统中的颜率法就可用来研究非线性系统的 1 基本特性。 称为描述函数的负倒数特性。 N(A) 描述函数法最重要的任务,则是非 线性元件描述函数N(4)的计算。下面 e N(A) G() 以典型非线性元件的描述函数为例,介 绍非线性元件函数的求解方法。 图8-8非线性控制系统等效结构图 8.2.3典型非线性元件的描述函数 1.,饱和特性的描述函数 x(t) (A 图89饱和非线性特性及输入输出波形图 图8-10饱和非线性特性的描述函 图&9所示为饱和非线性特性及其输入输出的波形图。当A<a时,工作在线性 段,没有非线性影响:当A≥☑时,工作在非线性段。因此饱和特性的描述函数, 只有在A≥a时才有意义。 由图8-8知,饱和特性为单值奇对称特性,其输出为一个周期性的奇函数,故
123 (8-8) 1 1 1 1 tan B − A = 仿照线性理论中频率特性的概念,非线性元件的等效幅相特性可用输出的基波 分量和输入正弦量的复数比来描述,即下式: A A j A B B A t g A A B A C A C N A 1 1 1 1 1 2 1 2 1 1 1 1 0 ( ) = + + = = = − 式中函数 N(A) 称为该非线性元件的描述函数。此描述函数 N(A) 是正弦输入 信号幅值 A 的函数。对非线性元件做了上述近似线性化处理后,图 8-6 所示的非线 性系统,可用图 8-8 来表示。这时线性系统中的频率法就可用来研究非线性系统的 基本特性。 ( ) 1 N A − 称为描述函数的负倒数特性。 描述函数法最重要的任务,则是非 线性元件描述函数 N(A) 的计算。下面 以典型非线性元件的描述函数为例,介 绍非线性元件函数的求解方法。 图 8-8 非线性控制系统等效结构图 8.2.3 典型非线性元件的描述函数 1.饱和特性的描述函数 图 8-9 饱和非线性特性及输入输出波形图 图 8-10 饱和非线性特性的描述函 图 8-9 所示为饱和非线性特性及其输入输出的波形图。当 A< a 时,工作在线性 段,没有非线性影响;当 A≥ a 时,工作在非线性段。因此饱和特性的描述函数, 只有在 A≥ a 时才有意义。 由图 8-8 知,饱和特性为单值奇对称特性,其输出为一个周期性的奇函数,故 e x c — — N(A) G(jω) -基波分量的相角 r

有A。=0,A=0,4=0。x)是对称波形,可只写出0~π2区段的表达式 「KAsin o0≤o≤0 x()= Ka 0sm≤月 (8-9) 式中0=sn1 A 由于输出波形的对称性,式(8-7)中A=0,只需确定B,。根据式(8-8)可 求得 B.-x()sin ond(cr) 4 [KAsin2 otd(ot)+Kasin otd(ot) 2m-9 π (A≥a) A 将以上关系代入式(8-8),从而求得饱和非线性特性的描述函数 M=马m导-9 Aπ (A≥a)(8-10) 由上式可见,饱和非线性特性的描述函数只与输入信号的幅值A有关,与频率。无 关。它等效为一个变系数的比例环节,而且在A>a时,等效传递系数总是小于线性 段的斜率K。若以alA为自变量,N(A)/K为因变量,可画出二者的关系曲线如图 &-10所示。当aA>1(即a>A)时,总是等于1,因为在线性区内,N(A)=K。 该图适合于不同K值的饱和特性。 2.死区非线性特性的描述函数 图&11所示为具有死区特性及输入输出波形图。当输入()=Asin ot时,其 输出x()为 0 0≤1≤0 x(t)=K(Asin ot-0) 0≤aot≤π-0 0 π-0≤a≤π 124
124 有 A0 = 0, A1 = 0,1 = 0。 x(t) 是对称波形,可只写出 0~π/2 区段的表达式 = 2 sin 0 ( ) Ka t KA t t x t 式中 A 1 a sin − = 。 由于输出波形的对称性,式(8-7)中 A1 = 0 ,只需确定 B1 。根据式(8-8)可 求得 = + − = = + − 1 2 2 0 2 2 0 1 sin 1 ( ) 2 sin ( ) sin ( ) 4 ( )sin ( ) 1 A a A a A KA a B x t t d t KA t d t Ka t d t 将以上关系代入式(8-8),从而求得饱和非线性特性的描述函数 = = + − 1 −1 2 sin 1 ( ) 2 ( ) A a A a A K a A B N A 由上式可见,饱和非线性特性的描述函数只与输入信号的幅值 A 有关,与频率ω无 关。它等效为一个变系数的比例环节,而且在 A> a 时,等效传递系数总是小于线性 段的斜率 K。若以 a /A 为自变量, N(A)/ K 为因变量,可画出二者的关系曲线如图 8-10 所示。当 a /A>1(即 a >A)时,总是等于 1,因为在线性区内, N(A) = K 。 该图适合于不同 K 值的饱和特性。 2.死区非线性特性的描述函数 图 8-11 所示为具有死区特性及输入输出波形图。当输入 e(t) = Asin t 时,其 输出 x(t) 为 − − − = t K A t t t x t 0 ( sin ) 0 0 ( ) (8-9) ( A a ) (8-10) ( A a )

式中0=s口,K为线性区的斜率。由于死区特性为单值奇对称,所以A。=0, A 4=0,4=0。代入式(8-7)可求得B,为 B=广te侧-usm-men (A≥a) 于是死区特性的描述函数为 (A≥a)(8-11) 这个函数也只有实部。N(A)/K与alA的关系曲线图8-11所示。 x(t) n(A 图811死区特性及输入输出波形图图8-12死区非线性特性的描述函数 3.继电器特性的描述函数 (1)死区-回环继电器特性的描述函数 图812是死区-回环继电器特性及其输入输出的波形图。其输出x()为 [b xt)={0 0≤t<1,02<ol<π+0,π+02<l≤2 π+01≤c1≤π+02
125 式中 A 1 a sin − = ,K 为线性区的斜率。由于死区特性为单值奇对称,所以 A0 = 0, A1 = 0,1 = 0 。代入式(8-7)可求得 B1 为 = − − − = = − − 1 2 2 2 0 1 sin 1 ( ) 2 2 ( sin )sin ( ) 4 ( )sin ( ) 1 A a A a A KA a B x t t d t K A t t d t 于是死区特性的描述函数为 = = − − − 1 −1 2 sin 1 ( ) 2 2 ( ) A a A a A K a A B N A 这个函数也只有实部。 N(A)/ K 与 a /A 的关系曲线图 8-11 所示。 图 8-11 死区特性及输入输出波形图 图 8-12 死区非线性特性的描述函数 3.继电器特性的描述函数 (1) 死区-回环继电器特性的描述函数 图 8-12 是死区-回环继电器特性及其输入输出的波形图。其输出 x(t) 为 − + + + + = 1 2 1 2 1 2 1 2 ( ) 0 0 , , 2 b t t t t b t x t ( A a ) ( A a ) (8-11)

020.060807 图813死区-回环继电器特性及输入 输出波形图 图8-14死区-回环继电器特性的描述函数 代入(8-7)的计算公式,得 ocosomd(or)cood(o) 资a- (A≥a) (8-12) on(c).shetd(on 学+ (A≥a) 从而求得死区-回环继电器特性的描述函数为 N(0=B+4 A -学+-婴m-)4ae (2)理想继电器特性的描述函数 如果图8-13中令a=0,就是理想继电器特性:令式(8-13)中a=0,得到理想 继电器特性的描述函数为 N(A)= (8-14) πA (A≥a) (3)死区继电器特性的描述函数 如果图8-13中令m=1,就是死区继电器特性:令式(8-13)中m=1,得到死区 继电器特性的描述函数为 126
126 图 8-13 死区-回环继电器特性及输入 输出波形图 图 8-14 死区-回环继电器特性的描述函数 代入(8-7)的计算公式,得 ( 1) 2 cos ( ) cos ( ) 1 2 1 2 1 1 = − = − + + m A ba A b t d t b t d t ( 1 ( ) 1 ( ) ) 2 sin ( ) sin ( ) 1 2 2 1 2 1 2 1 A a A b ma B b t d t b t d t = − + − = − + + 从而求得死区-回环继电器特性的描述函数为 ( 1) 2 1 ( ) 1 ( ) 2 ( ) 2 2 2 1 1 + − = − + − + = m A ba j A a A ma A b A B jA N A (2) 理想继电器特性的描述函数 如果图 8-13 中令 a =0,就是理想继电器特性;令式(8-13)中 a =0,得到理想 继电器特性的描述函数为 A b N A 4 ( ) = (3) 死区继电器特性的描述函数 如果图 8-13 中令 m=1,就是死区继电器特性;令式(8-13)中 m =1,得到死区 继电器特性的描述函数为 (8-12) ( A a ) ( A a ) ( A a ) (8-13) ( (8-14) A a )