
自动控制理论 第二章控制系统的数学模型 新疆大学电气工程学院 2025/1114
2025/1/14 第二章控制系统的数学模型 新疆大学 电气工程学院 自动控制理论

自动控制理论 描述系统运动的数学模型 >输入-输出描述 微分方程是这种描述的最基本形式。传递函数、方框图 等其它模型均由它而导出 >状态变量描述 状态方程是这种描述的最基本形式 米建立系统数学模型的方法 > 实验法 >解析法 第二章控制系统的数学模型 2025/1/14
2 第二章 控制系统的数学模型 2025/1/14 描述系统运动的数学模型 自动控制理论 ➢状态变量描述 状态方程是这种描述的最基本形式 建立系统数学模型的方法 ➢ 实验法 ➢ 解析法 ➢ 输入-输出描述 微分方程是这种描述的最基本形式。传递函数、方框图 等其它模型均由它而导出

自动控制理论 第一节列写系统微分方程的一般方法 *用解析法建立系统微分方程的一般步骤 >根据基本的物理定律,列写出系统中一个元件的输入与输出的微分方程 式 > 确定系统的输入量与输出量,消去其余的中间变量,求得系统输出与输 入的微分方程式 例2-1求Uc与Ur的微分方程式 R+1 +u。=u, 解:由基尔霍夫定律得 dt 即i=cdue dt 消去中间变量,则有: dt 图2-1R-L-C电路 3 第二章控制系统的数学模型 2025/1/14
第一节 列写系统微分方程的一般方法 用解析法建立系统微分方程的一般步骤 dt du idt i C C u u u dt di iR l c c c r = = + + = , 即 1 第二章 控制系统的数学模型 2025/1/14 3 自动控制理论 ➢ 根据基本的物理定律,列写出系统中一个元件的输入与输出的微分方程 式 ➢ 确定系统的输入量与输出量,消去其余的中间变量,求得系统输出与输 入的微分方程式 图2-1 R-L-C电路 例2-1求Uc与Ur的微分方程式 解:由基尔霍夫定律得 c r c c u u dt du RC dt d u LC + + = 2 2 消去中间变量 i ,则有:
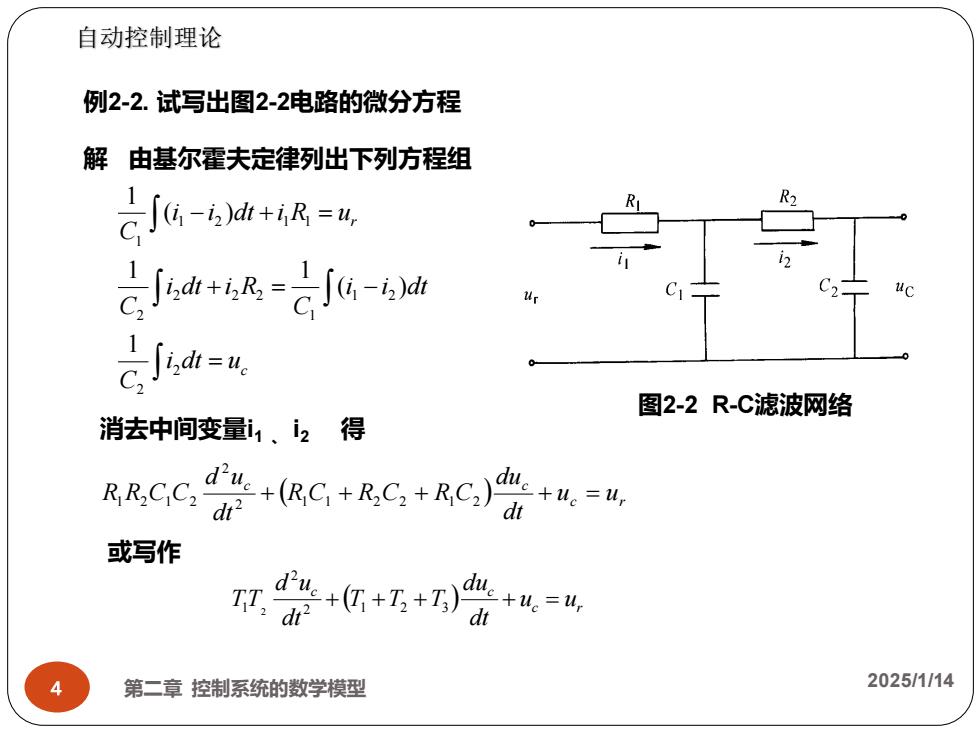
自动控制理论 例2-2.试写出图2-2电路的微分方程 解由基尔霍夫定律列出下列方程组 Cu-i+R-u +6&-2m fou 图2-2R-C滤波网络 消去中间变量1、2得 RRCG器+(风G+见G+RG)陪+=% 或写作 ++不+路+= TT:dr 第二章控制系统的数学模型 2025/1/14
c r i dt u C i i dt C i dt i R C i i dt i R u C = + = − − + = 2 2 1 2 1 2 2 2 2 1 2 1 1 1 1 ( ) 1 1 ( ) 1 1 i ( ) c r c c u u dt du R C R C R C dt d u R R C C + 1 1 + 2 2 + 1 2 + = 2 2 1 2 1 2 ( ) c r c c u u dt du T T T dt d u TT + 1 + 2 + 3 + = 2 2 1 2 第二章 控制系统的数学模型 2025/1/14 4 自动控制理论 图2-2 R-C滤波网络 例2-2. 试写出图2-2电路的微分方程 解 由基尔霍夫定律列出下列方程组 消去中间变量i1 、 i2 得 或写作
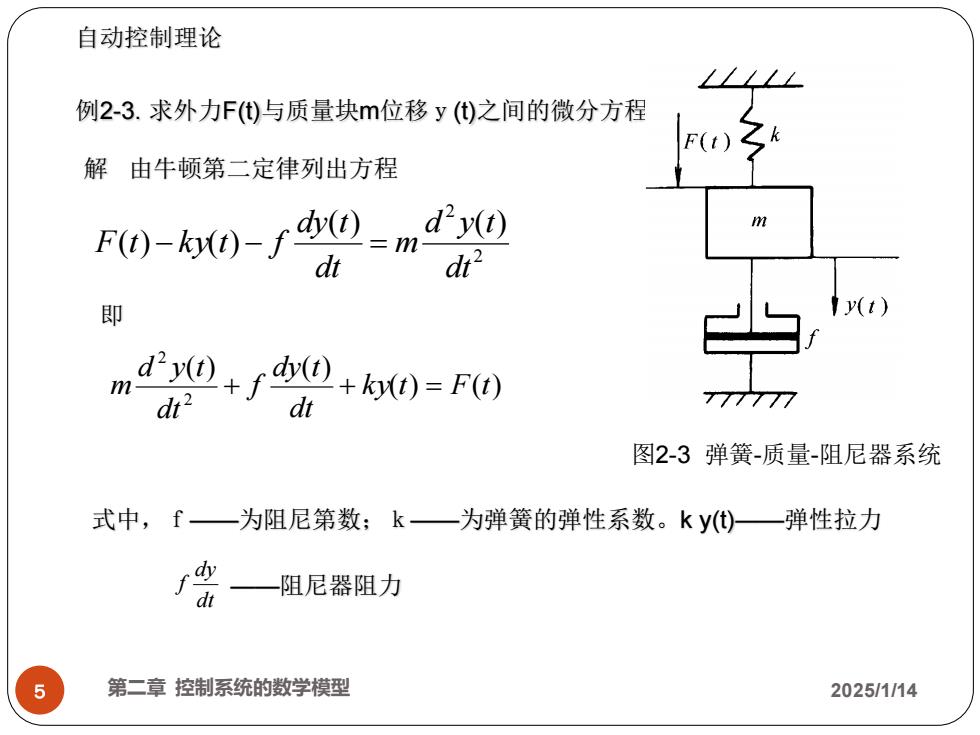
自动控制理论 例2-3.求外力F()与质量块m位移y()之间的微分方程 F()之k 解由牛顿第二定律列出方程 F0-0-f40-m0 dt 即 d@+f0+0=F0 m dt2 dt 777777 图2-3弹簧-质量-阻尼器系统 式中,f一为阻尼第数;k一为弹簧的弹性系数。ky)—弹性拉力 阻尼器阻力 5 第二章控制系统的数学模型 2025/1/14
5 第二章 控制系统的数学模型 2025/1/14 2 2 ( ) ( ) ( ) ( ) dt d y t m dt dy t F t − k y t − f = ( ) ( ) ( ) ( ) 2 2 k y t F t dt dy t f dt d y t m + + = 自动控制理论 例2-3. 求外力F(t)与质量块m位移y(t)之间的微分方程 解 由牛顿第二定律列出方程 图2-3 弹簧-质量-阻尼器系统 即 式中,f——为阻尼第数;k——为弹簧的弹性系数。k y(t)——弹性拉力 dt dy f ——阻尼器阻力
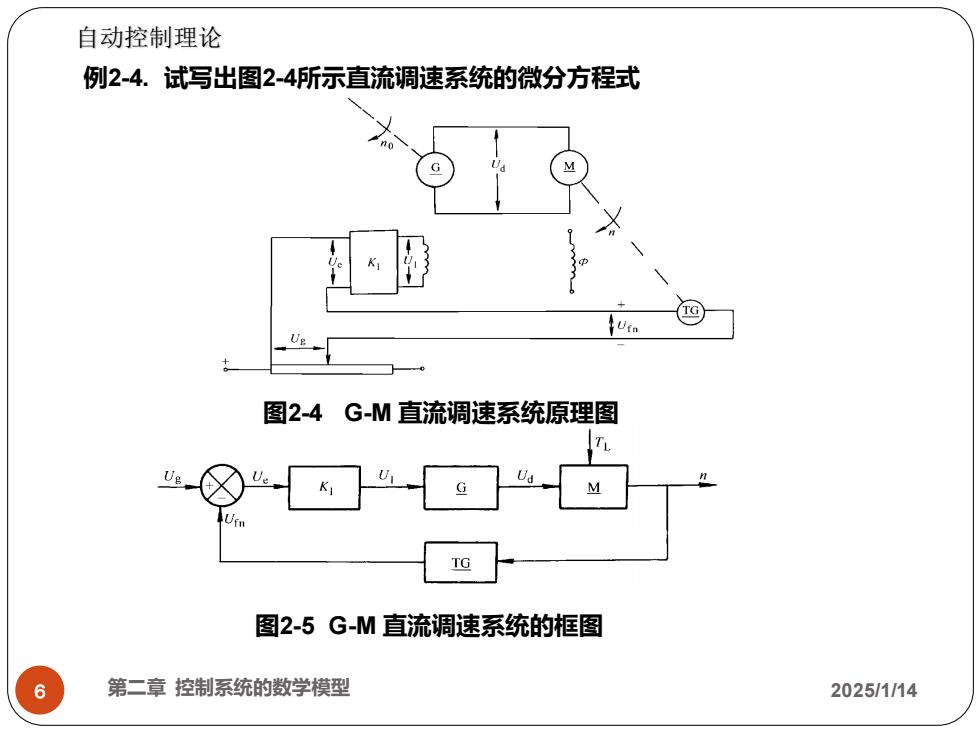
自动控制理论 例2-4.试写出图2-4所示直流调速系统的微分方程式 图2-4G-M直流调速系统原理图 TG 图2-5G-M直流调速系统的框图 6 第二章控制系统的数学模型 2025/1/14
6 第二章 控制系统的数学模型 2025/1/14 自动控制理论 例2-4. 试写出图2-4所示直流调速系统的微分方程式 图2-5 G-M 直流调速系统的框图 图2-4 G-M 直流调速系统原理图
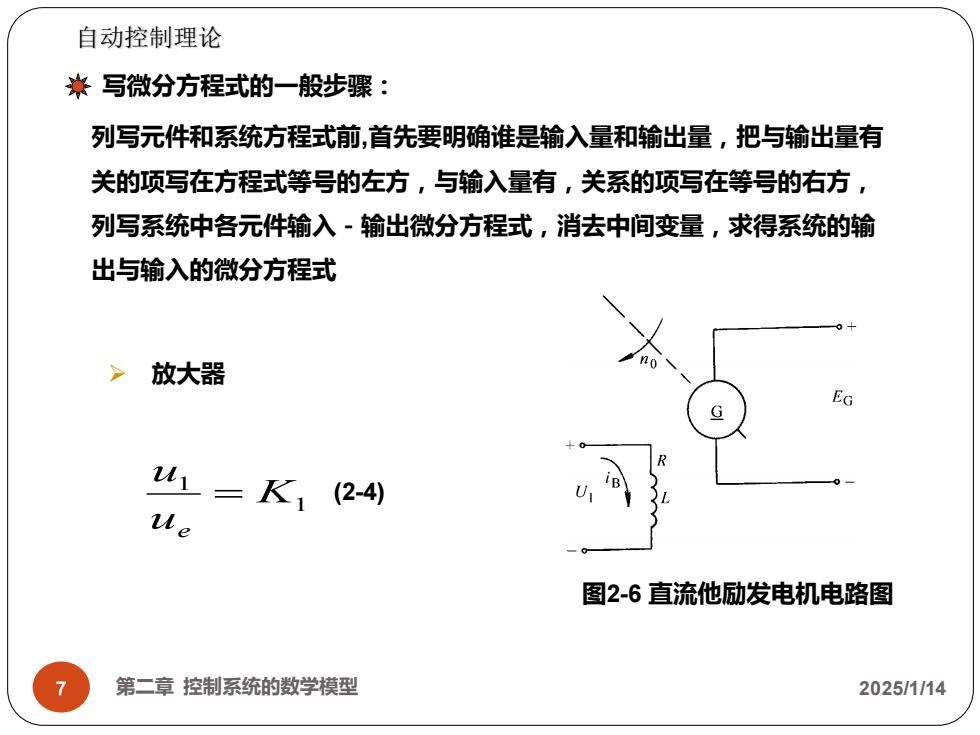
自动控制理论 嶚写微分方程式的一般步骤: 列写元件和系统方程式前,首先要明确谁是输入量和输出量,把与输出量有 关的项写在方程式等号的左方,与输入量有,关系的项写在等号的右方, 列写系统中各元件输入-输出微分方程式,消去中间变量,求得系统的输 出与输入的微分方程式 > 放大器 EG u=K (2-4) 图2-6直流他励发电机电路图 第二章控制系统的数学模型 2025/1/14
7 第二章 控制系统的数学模型 2025/1/14 自动控制理论 列写元件和系统方程式前,首先要明确谁是输入量和输出量,把与输出量有 关的项写在方程式等号的左方,与输入量有,关系的项写在等号的右方, 列写系统中各元件输入-输出微分方程式,消去中间变量,求得系统的输 出与输入的微分方程式 ➢ 放大器 图2-6 直流他励发电机电路图 1 1 K u u e = (2-4) 写微分方程式的一般步骤:
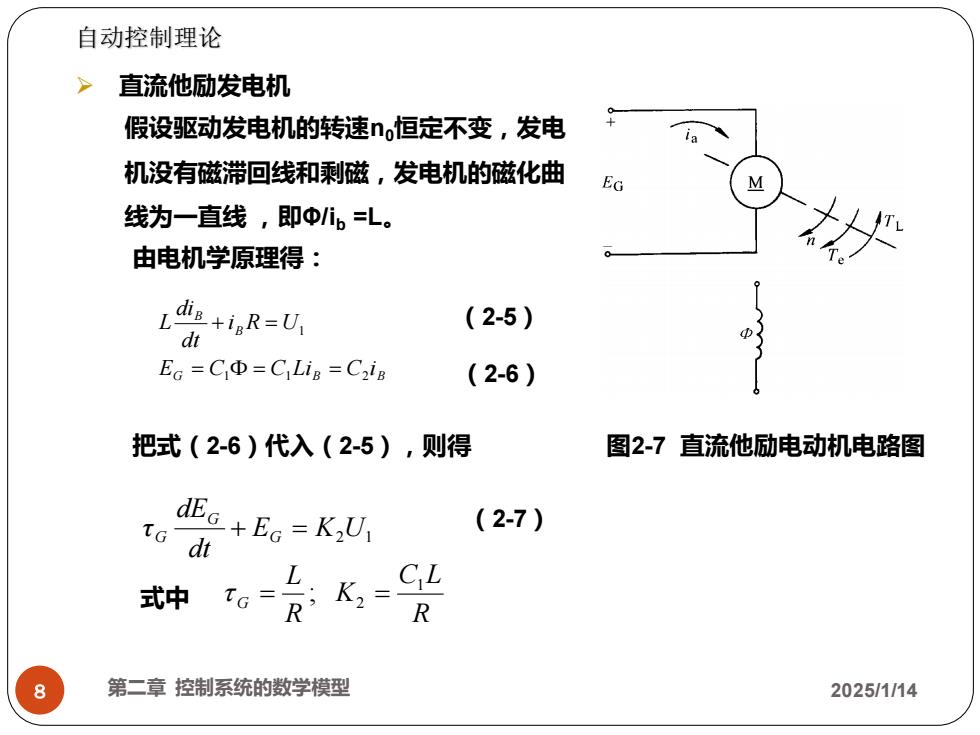
自动控制理论 >直流他励发电机 假设驱动发电机的转速no恒定不变,发电 机没有磁滞回线和剩磁,发电机的磁化曲 EG M 线为一直线,即0ib=L。 由电机学原理得: Ldin+igR=U (2-5) dt EG =CD=CLig =C2iB (2-6) 把式(2-6)代入(2-5),则得 图2-7直流他励电动机电路图 dEc+Ea=KU tG dt (2-7) R 8 第二章控制系统的数学模型 2025/1/14
8 第二章 控制系统的数学模型 2025/1/14 G B B B B E C C Li C i i R U dt di L 1 1 2 1 = = = + = R C L K R L G 1 2 = ; = E K2 U1 dt dE τ G G G + = 自动控制理论 ➢ 直流他励发电机 由电机学原理得: 把式(2-6)代入(2-5),则得 图2-7 直流他励电动机电路图 (2-5) (2-6) (2-7) 式中 假设驱动发电机的转速n0恒定不变,发电 机没有磁滞回线和剩磁,发电机的磁化曲 线为一直线 ,即Φ/ib =L

自动控制理论 >直流他励电动机 被控制量是电动机的转速n控制量:发电机的电动势Ec和负载转矩TL, 由基尔霍夫定律和牛顿第二定律得 。R+L -+Cn=Ea 1-1=375di GD2 dn T。=Cwia 消去上述方程中的中间变量T和,求得 (2-8) 式中,tn GDR称为电动机的机电时间常数:。 375C 称为电动机的电气时间常数 当T=0时,电动机空载运行至稳态时,式(2-8)便蜕化为 n=云EG (n,为电动机的空载转速) (2-9) Ce ! 第二章控制系统的数学模型 2025/1/14
( ) ( 2 -9) 1 0 2 8 375 ( 2 -8) 1 375 0 0 2 2 2 2 ( 为电动机的空载转速) 当 时,电动机空载运行至稳态时,式 便蜕化为 式中, 称为电动机的机电时间常数; 称为电动机的电气时间常数 消去上述方程中的中间变量 和 求得 E n C n T R L C G D R dt dT T C C R E C n dt dn dt d n T i , T C i dt G D dn T T C n E dt di i R L G e L a u m L L a e u G e m a m e a e u a e L e G a a = = − = + + = − + = − = + + = 第二章 控制系统的数学模型 2025/1/14 9 自动控制理论 ➢ 直流他励电动机 被控制量是电动机的转速n控制量:发电机的电动势EG和负载转矩TL。 由基尔霍夫定律和牛顿第二定律得

自动控制理论 >测速发电机 输入量是电动机的转速n,输出量是测速发电机的电压Um,假设 测速发电机的磁场恒定不变,则Un与成线性关系即有 u =an (2-10) 而 ue =ug-us (2-11) 引起系统运动的输入量是经定电压u和负载转矩T(扰动),电 动机的转速n为系统的输出量,经消元后得 d'n ++7路+7 (2-12) 式中,K=KK2,R=RG+Rm 10 第二章控制系统的数学模型 2025/1/14
10 第二章 控制系统的数学模型 2025/1/14 输入量是电动机的转速n,输出量是测速发电机的电压Ufn ,假设 测速发电机的磁场恒定不变,则Ufn与n成线性关系即有 动机的转速n为系统的输出量,经消元后得 引起系统运动的输入量是经定电压u 和负载转矩T (扰动),电 而 g L u u - u (2 -11) u an (2 -10) e g fn fn = = ➢ 测速发电机 ( ) ( ) ( ) (2 -12) 1 2 2 2 2 3 3 T dt dT τ T dt d T τ τ C C R U C K n C Ka dt dn τ τ dt d n τ τ τ dt d n τ τ τ L L a G L G a e u g e e m a G m a G G m = − + + + + + + + + + 1 2 R R G R m 式中, K = K K , = + 自动控制理论