
自动控制理论 第三章控制系统的时域分析 新腰大学电气工程学院
第三章控制系统的时域分析 新疆大学电气工程学院 自动控制理论

自动控制理论 第一节典型的试验信号 染典型的试验信号一般应具备两个条件 (1)信号的数学表达式要简单 (2)信号易于在实验室中获得 一、 阶跃输入 t<0 t≥0 图3-1 式中,R,=常量。R,=山,则称为单位阶跃信号,它的拉氏变换为RS)= 第三章控制系统的时域分析 2025/1/14
第一节 典型的试验信号 典型的试验信号一般应具备两个条件 ( ) s 1 R 1 式中,R0 = 常量。R0 = ,则称为单位阶跃信号,它的拉氏变换为 s = 2 第三章 控制系统的时域分析 2025/1/14 自动控制理论 (1)信号的数学表达式要简单 (2)信号易于在实验室中获得 一、阶跃输入 图3-1 ( ) = t 0 0 t 0 R0 r t <

自动控制理论 二、斜坡信号 0)= vot t≥0 t<0 若。=1,称为单位斜坡信号,拉氏变换为%: 三、等加速度信号 等加速度信号是一种抛物线函数,其数学表达式为 01 t<0 r0)= 1 t≥0 a,=常数,若a,=山称为单位等加速度信号,拉氏变换为 3 第三章控制系统的时域分析 2025/1/14
3 第三章 控制系统的时域分析 2025/1/14 0 2 1 1 s 若v = ,称为单位斜坡信号,拉氏变换为 0 0 3 a a 1 1 s = 常数,若 = ,称为单位等加速度信号,拉氏变换为 自动控制理论 三、等加速度信号 等加速度信号是一种抛物线函数,其数学表达式为 ( ) = a t t 0 2 1 t 0 2 0 1 < r t 二、斜坡信号 ( ) = t 0 0 t 0 < v t r t
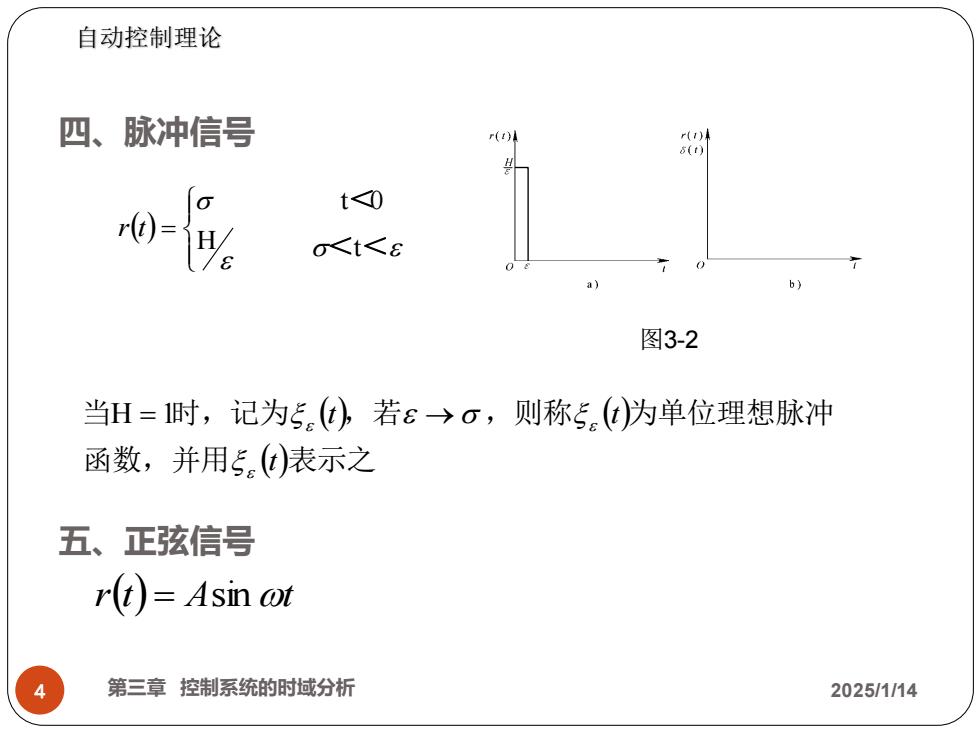
自动控制理论 四、脉冲信号 r() r(1)米 6(t) t<0 0<t<8 b) 图3-2 当H=时,记为5()若ε→o,则称5(d为单位理想脉冲 函数,并用5)表示之 五、正弦信号 r(t)=Asin ot 第三章控制系统的时域分析 2025/1/14
4 第三章 控制系统的时域分析 2025/1/14 ( ) ( ) 函数,并用 ( )表示之 当 时,记为 ,若 ,则称 为单位理想脉冲 t t t H = 1 → r(t) = Asint 五、正弦信号 自动控制理论 四、脉冲信号 图3-2 ( ) = < < < H t t 0 r t
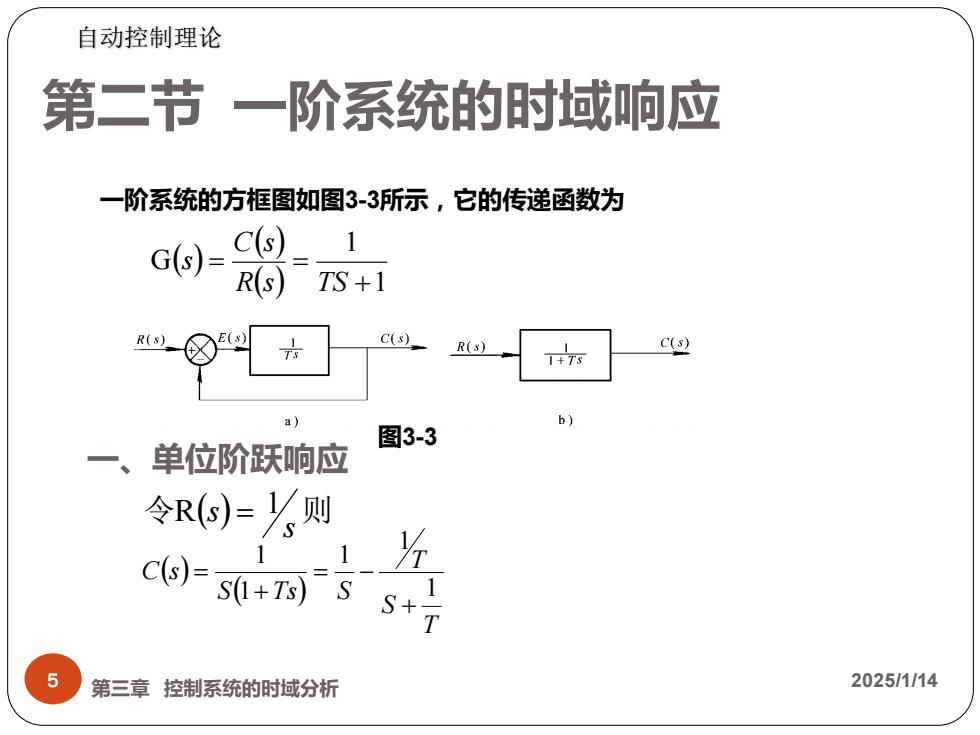
自动控制理论 第二节一阶系统的时域响应 一阶系统的方框图如图3-3所标,它的传递函数为 G6)= C(s) 1 R(s) TS+1 c(s) R(s) C(s) a) 图3-3 单位阶跃响应 令R6)=则 1 C(s)=s(1+7s)s S*T 5 第三章控制系统的时域分析 2025/1/14
第二节 一阶系统的时域响应 ( ) ( ) ( ) 1 1 G + = = R s TS C s s 5 第三章 控制系统的时域分析 2025/1/14 一阶系统的方框图如图3-3所示,它的传递函数为 图3-3 自动控制理论 一、单位阶跃响应 令 ( ) 则s R s = 1 ( ) ( ) T S T S Ts S C s 1 1 1 1 1 + = − + =

自动控制理论 c0=1-e7 当T=时,则有: C(T)=1-e7=0.63 阶跃响应曲线C(t)上升到其终值的63.27,对应的时间就是系统的时间 常数T 二、单位斜坡响应 令R)=为则 1T,T2 C8)s0+丙s2-s+1+S c0-币 2025/11/14 6 第三章控制系统的时域分析
C(T) 1- 0.63 1 = = − T e 2025/1/14 6 第三章 控制系统的时域分析 阶跃 响应曲线 C(t)上升到其终值的63.27,对应的时间就是系统的时间 常数T 自动控制理论 ( ) t T C t e 1 1 − = − 当T = t时,则有: 二、单位斜坡响应 令R( ) 1 2 则 s s = ( ) ( ) 1 TS T S 1 T 1 1 2 2 2 + = − + + = S Ts S C s ( ) = − − − t T C t t T e 1 1

自动控制理论 0=0-c0=-e ess lim e(t)=T 1)00 三、单位脉冲响应 令)=s),则系统的输出 C6=Gs)= 1 S*了 g6=rGo=7e子 米线性定常系统的性质 (1)一个输入信号导数的时域响应高于该输入信号的时域响应的导数 (2)一个输入信号积分的时域响应高于该输入信号的时域响应的积分 结论:了解一种典型信号的响应,就可据知于其它信号作用下的响应。 第三章控制系统的时域分析 2025/1/14
ess ( ) T t = = → lim e t 第三章 控制系统的时域分析 2025/1/14 7 自动控制理论 ( ) ( ) ( ) = − = − − t T r t C t T e 1 e t 1 三、单位脉冲响应 令r(t) = s(t),则系统的输出 ( ) ( ) T S T C s G s 1 1 + = = ( ) ( ) t T e T g s L G s 1 1 1 − − = = 线性定常系统的性质 (1)一个输入信号导数的时域响应高于该输入信号的时域响应的导数 (2)一个输入信号积分的时域响应高于该输入信号的时域响应的积分 结论:了解一种典型信号的响应,就可据知于其它信号作用下的响应
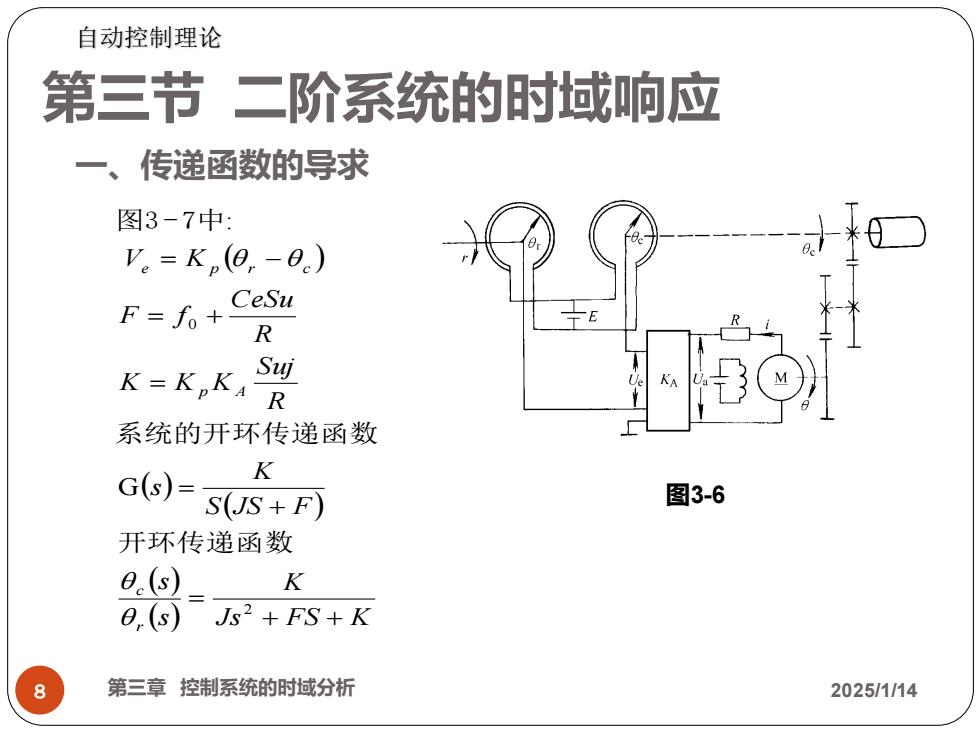
自动控制理论 第三节二阶系统的时域响应 一、传递函数的导求 图3-7中: V。=K(0,-0e) F=f。+ CeSu R K=KpKA R j 系统的开环传递函数 G(s)= K S(JS+F) 图3-6 开环传递函数 0.(s) K 0,(s)Js2+FS+K 第三章控制系统的时域分析 2025/1/14
第三节 二阶系统的时域响应 8 第三章 控制系统的时域分析 2025/1/14 ( ) ( ) ( ) ( ) ( ) Js FS K K s s S JS F K s R Suj K K K R CeSu F f V K r c p A e p r c + + = + = = = + = − 2 0 G : 开环传递函数 系统的开环传递函数 图3 - 7中 一、传递函数的导求 图3-6 自动控制理论

自动控制理论 ⊙(s) 8-□囚☒园回 阳迈 ⊙(s) K oc 5(5+F) 图3-7图3-6所示系统的框图及简化框图 二、二阶系统的单位阶跃响应 标准形式: C(s) (3-13) R(S)s2+25o”s+0n 为系统的阻尼比;o为系统的无阻尼自然频率 9 第三章控制系统的时域分析 2025/1/14
9 第三章 控制系统的时域分析 2025/1/14 图3-7 图3-6所示系统的框图及简化框图 自动控制理论 二、二阶系统的单位阶跃响应 标准形式: ( ) ( ) (3-13) 2 2 2 2 n n n R s s s C s + + = 为系统的阻尼比;n为系统的无阻尼自然频率

自动控制理论 R(s) on C(s) s(s+26@n) 图3-8二阶系统的框图 1、欠阻尼0<5<) s12=-50,+j0nV1-52=-50n+j01 令R)=1,则 Q, 1 s+50n 50n C6)=+aF+o]g+5a,广+o (s+50)2+0a c0-cn时tad 10 第三章控制系统的时域分析 2025/1/14
10 第三章 控制系统的时域分析 2025/1/14 图3-8 二阶系统的框图 自动控制理论 1、 欠阻尼(0<<1) n n n d = − + j − = − + j 2 1.2 s 1 令 ( ) ,则 s R s 1 = ( ) ( ) ( ) ( ) 2 2 2 2 2 2 2 1 n d n n d n n d n s s s s s s C s + + − + + + = − + + = ( ) sin (t 0) 1 1 cos 2 − = − + − C t e t t d d t n