
第七章离散控制系统 7.1引言 离散控制系统与连续控制系统的根本区别,在于连续控制系统中的信号都是时 间的连续函数,而离散控制系统中有一处或多处的信号是脉冲序列或数码形式的。 离散系统与连续系统相比,既有本质上的不同,又有分析研究方面的相似性。 利用2变换法研究离散系统,可以将连续系统中的许多概念和方法,推广应用于线 性离散系统。 典型的计算机控制系统即为离散系统的一种。其原理图如下: ========男 r(t) u.(t0 A/D 数字控制器→DA 被控对象 数字计算机 测量元件 图7一1计算机控制系统典型原理图 离散控制系统的特点: 1.校正装置效果比连续式校正装置好,且由软件实现的控制规律易于改变,控制 灵活。 2.采样信号,特别是数字信号的传递能有效地抑制噪声,从而提高系统抗干扰能力。 3.可用一台计算机分时控制若干个系统,提高设备利用率。 4.可实现复杂控制规律,且可以在运行中实时改变响应参数。 72信号的采样与复现 把连续信号变为离散信号的过程叫做采样,实现采样的装置称为采样器(采样 开关)。反之,把采样后的离散信号恢复为连续信号的过程称为信号的复现。 f() f( 105
105 第七章 离散控制系统 7.1 引言 离散控制系统与连续控制系统的根本区别,在于连续控制系统中的信号都是时 间的连续函数,而离散控制系统中有一处或多处的信号是脉冲序列或数码形式的。 离散系统与连续系统相比,既有本质上的不同,又有分析研究方面的相似性。 利用 z 变换法研究离散系统,可以将连续系统中的许多概念和方法,推广应用于线 性离散系统。 典型的计算机控制系统即为离散系统的一种。其原理图如下: 离散控制系统的特点: 1. 校正装置效果比连续式校正装置好,且由 软件实现的控制规律易于改变,控制 灵活。 2. 采样信号,特别是数字信号的传递能有效地抑制噪声,从而提高系统抗干扰能力。 3. 可用一台计算机分时控制若干个系统,提高设备利用率。 4. 可实现复杂控制规律,且可以在运行中实时改变响应参数。 7.2 信号的采样与复现 把连续信号变为离散信号的过程叫做采样,实现采样的装置称为采样器(采样 开关)。反之,把采样后的离散信号恢复为连续信号的过程称为信号的复现。 A/D 数字控制器 D/A 被控对象 测量元件 e*(t)数字计算机 r(t) e(t) u*(t) uh(t) c(t) _ 图7-1 计算机控制系统典型原理图 采样 t t T ( ) * f t s f (t) 0 0 t ( ) * f t 0 T 采样 t t T ( ) * f t s f (t) 0 0 t ( ) * f t 0 T 采样 t t T ( ) * f t s f (t) 0 0 t ( ) * f t 0 T

图7-2采样过程 采样信号:f0)=∑fkT)心(-kD A-0 离散控制系统的采样定理给出了从采样的离散信号恢复到原来连续信号所必须 的最低采样频率(0,≥20x)。 采样定理可叙述如下:如果采样周期满足下列条件,即 0,=2π/T>20m 或 T<π/om 式中⊙为连续信号f(t)的最高次谐波的角频率。则采样信号f*()就可以 无失真地再恢复为原连续信号∫()。这就是说,如果选择的采样角频率足够高,使 得对连续信号所含的最高次谐波,能做到在一个周期内采样两次以上的话,那么经 采样后所到的脉冲列试句含了原续信的全部信息。右可能桶时理相 波器把原信号毫无失真地恢复出来, 否则采样频率过低,信息损失很多, 原信号就 不能准确复现 采样周期的选择:采样周期T越小,控制效果越好,将增加计算负担且T小到 一定程度,无多大实际意义:反之,采样周期T过大,误差较大,甚至导致整个控 制系统失去稳定。 离散信号的恢复,是在系统中加入代替理想滤波器的实际保持器来实现的。按 恒值外推规律实现的零阶保持器,由于其实现简单,且具有最小的相移,被广泛的 应用于离散控制系统中,其传递函数为 G,(s)=1-e-h 7.3Z变换与Z反变换 线性连续控制系统可用线性微分方程来描述,用拉氏变换分析它的暂态性能及 稳态性能。对于线性离散控制系统则可用线性差分方程来描述,用Z变换来分析它 的暂态性能及稳态性能。Z变换是研究离散系统主要的数学工具,由拉氏变换引导 出来,是离散信号的拉氏变换。 1.:变换定义 变换实质上是拉氏变换的一种扩展,也称作采样拉氏变换。在采样系统中 连续函数信号∫()经过采样开关,变成采样信号∫*()
106 图 7-2 采样过程 采样信号: 离散控制系统的采样定理给出了从采样的离散信号恢复到原来连续信号所必须 的最低采样频率( s 2 max )。 采样定理可叙述如下:如果采样周期满足下列条件,即 2 max s = 2 /T 或 max T / 式中 max 为连续信号 f (t) 的最高次谐波的角频率。则采样信号 f * (t) 就可以 无失真地再恢复为原连续信号 f (t) 。这就是说,如果选择的采样角频率足够高,使 得对连续信号所含的最高次谐波,能做到在一个周期内采样两次以上的话,那么经 采样后所得到的脉冲序列,就包含了原连续信号的全部信息。就有可能通过理想滤 波器把原信号毫无失真地恢复出来。否则采样频率过低,信息损失很多,原信号就 不能准确复现。 采样周期的选择:采样周期 T 越小,控制效果越好,将增加计算负担,且 T 小到 一定程度,无多大实际意义;反之,采样周期 T 过大,误差较大,甚至导致整个控 制系统失去稳定。 离散信号的恢复,是在系统中加入代替理想滤波器的实际保持器来实现的。按 恒值外推规律实现的零阶保持器,由于其实现简单,且具有最小的相移,被广泛的 应用于离散控制系统中,其传递函数为 s e G s Ts h − − = 1 ( ) 7.3 Z 变换与 Z 反变换 线性连续控制系统可用线性微分方程来描述,用拉氏变换分析它的暂态性能及 稳态性能。对于线性离散控制系统则可用线性差分方程来描述,用 Z 变换来分析它 的暂态性能及稳态性能。Z 变换是研究离散系统主要的数学工具,由拉氏变换引导 出来,是离散信号的拉氏变换。 1. z 变换定义 z 变换实质上是拉氏变换的一种扩展,也称作采样拉氏变换。在采样系统中, 连续函数信号 f (t) 经过采样开关,变成采样信号 f * (t) = = − 0 * ( ) ( ) ( ) k f t f kT t kT

∫*0=∑fk60-k切 对上式进行拉氏变换 F*o=ol-2nt (7-1) 从此式可以看出,任何采样信号的拉氏变换中,都含有超越函数如,因此,若仍 用拉氏变换处理采样系统的问题,就会给运算带来很多困难,为此,引入新变量:, 2=eh (7-2) 将F*(S)记作F(),则式(7-1)可以改写为 Fe)=∑fkT= (7-3) A=0 这样就变成了以复变量:为自变量的函数。称此函数为∫*()的:变换。记作 F()=Zf*(t] 因为:变换只对采样点上信号起作用,所以上式也可以写为 F()=Zf()] 应注意,F()是f()的:变换符号,其定义就是式(7-3),不要误以为它是f() 的拉氏变换式F()中的s以:简单置换的结果。将式(7一3)展开 F(a)=f0)z°+fT)z+f(2Tz2+.+fkTz-*+. (7-4) 可见,采样函数的:变换是变量:的幂级数。其一般项(kTz具有明确的物理意 义: 107
107 = = − 0 *( ) ( ) ( ) k f t f kT t kT 对上式进行拉氏变换 = − = = 0 *( ) £ *( ) ( ) k kTs F s f t f k T e (7-1) 从此式可以看出,任何采样信号的拉氏变换中,都含有超越函数 kTs e − ,因此,若仍 用拉氏变换处理采样系统的问题,就会给运算带来很多困难,为此,引入新变量 z , 令 z = Ts e (7-2) 则 z T s ln 1 = 将 F *(s)记作F(z) ,则式(7-1)可以改写为 = − = 0 ( ) ( ) k k F z f kT z (7-3) 这样就变成了以复变量 z 为自变量的函数。称此函数为 f * (t) 的 z 变换。记作 F(z) = Zf *(t) 因为 z 变换只对采样点上信号起作用,所以上式也可以写为 F(z) = Zf (t) 应注意, F(z) 是 f (t) 的 z 变换符号,其定义就是式(7-3),不要误以为它是 f (t) 的拉氏变换式 F(s) 中的 s 以 z 简单置换的结果。将式(7-3)展开 F(z) = f (0)z 0 + f (T)z −1 + f (2T)z −2 ++ f (k T)z −k + (7-4) 可见,采样函数的 z 变换是变量 z 的幂级数。其一般项 k f kT z − ( ) 具有明确的物理意 义:

f(kT)表示采样脉冲的幅值::的幂次表示该采样脉冲出现的时刻。因此它包 含着量值与时间的概念。 2.变换的求法 (1)用定义求 已知时函数f),则 zol=fD= k=0 展开后,根据无穷级数求和公式 a+ag+a时+品g英中M1 即可求出函数的:变换。 (②)用查表法求 若己知函数的拉氏变换(象函数),用部分分式法将其展开,查表对应即可。 3.:反变换 正如同在拉氏变换方法中一样,:变换方法的一个主要目的是要先获得时域函 数f()在:域中的代数解,其最终的时域解可通过反:变换求出。当然,F(:)的 反:变换只能求出∫*(),即只能是∫(k)。如果是理想采样器作用于连续信号 f(),则在1=kT瞬间的采样值f(kT)可以获得。:反变换可以记作 Z-[F()]=f*( (7-5) 求:反变换的方法通常有以下三种: ()部分分式展开法 (2)级数展开法(综合除法) (3)留数法 在求:反变换时,仍假定当k<0时,f(kT)=0。下面介绍最常用的两种求:反变 换的方法。 108
108 f (kT) 表示采样脉冲的幅值; z 的幂次表示该采样脉冲出现的时刻。因此它包 含着量值与时间的概念。 2. z 变换的求法 (1) 用定义求 已知时函数 f (t) ,则 = − = 0 ( ) ( ) k k Z f t f kT z 展开后,根据无穷级数求和公式 q a a aq aq − + + + = 1 2 ,其中 q 1 即可求出函数的 z 变换。 (2) 用查表法求 若已知函数的拉氏变换(象函数),用部分分式法将其展开,查表对应即可。 3. z 反变换 正如同在拉氏变换方法中一样, z 变换方法的一个主要目的是要先获得时域函 数 f (t) 在 z 域中的代数解,其最终的时域解可通过反 z 变换求出。当然, F(z) 的 反 z 变换只能求出 f * (t) ,即只能是 f (kt) 。如果是理想采样器作用于连续信号 f (t) ,则在 t = kT 瞬间的采样值 f (kT) 可以获得。 z 反变换可以记作 ( ) *( ) 1 Z F z = f t − (7-5) 求 z 反变换的方法通常有以下三种: (1) 部分分式展开法 (2) 级数展开法(综合除法) (3) 留数法 在求 z 反变换时,仍假定当 k 0 时, f (kT) = 0 。下面介绍最常用的两种求 z 反变 换的方法

(1)部分分式展开法 此法是将F()通过部分分式分解为低阶的分式之和,直接从:变换表中求出各项对 应的:反变换,然后相加得到∫(kT刀)。 7.4脉冲传递函数 1.脉冲传递函数的定义 零初始条件下,线性定常离散系统输出的:变换与输入的:变换之比,称为脉 冲传递函数。 2.串联环节的脉冲传递函数 假定输出变量前有采样开关(或有一理想的虚拟采样开关),或者输入变量后有 采样开关。则我们分析下面二种情况: (1)二串联环节间有采样开关 图7-3(a)所示两个串联环节间有采样器隔开,所以有 U(z)=G()R() (7-6) C(=)=G2(U,() (7-7) 式中G,(:)、G,(:)分别为线性环节G,(S)、G,(S)的脉冲传递函数,即 G()=ZG(s小,G,()=ZG(s小,则由式(7-6)和(7-7)可得 C(=G()G(R( 所以,图7-3(a)所示系统的脉冲传递函数为 ce-Q-Gec, R() 可见,两个环节间有采样器隔开时,则环节串联等效脉冲传递函数为两个环节的脉 冲传递函数的乘积。同理,n个环节串联,且所有环节之间均有采样器隔开时,则 等效脉冲传递函数为所有环节的脉冲传递函数的乘积。即 G)=G,(a)G2(a).Gn(a) (7-8) 109
109 (1) 部分分式展开法 此法是将 F(z) 通过部分分式分解为低阶的分式之和,直接从 z 变换表中求出各项对 应的 z 反变换,然后相加得到 f (kT) 。 7.4 脉冲传递函数 1.脉冲传递函数的定义 零初始条件下,线性定常离散系统输出的 z 变换与输入的 z 变换之比,称为脉 冲传递函数。 2.串联环节的脉冲传递函数 假定输出变量前有采样开关(或有一理想的虚拟采样开关),或者输入变量后有 采样开关。则我们分析下面二种情况: (1) 二串联环节间有采样开关 图 7-3(a)所示两个串联环节间有采样器隔开,所以有 ( ) ( ) ( ) (7 7) ( ) ( ) ( ) (7 6) 2 1 1 1 = − = − C z G z U z U z G z R z 式中 ( ) 1 G z 、 ( ) 2 G z 分别为线性环节 ( ) 1 G s 、 ( ) 2 G s 的脉冲传递函数,即 ( ) ( ) 1 1 G z = Z G s , ( ) ( ) 2 2 G z = Z G s ,则由式(7-6)和(7-7)可得 ( ) ( ) ( ) ( ) 1 2 C z = G z G z R z 所以,图 7-3(a)所示系统的脉冲传递函数为 ( ) ( ) ( ) ( ) ( ) 1 2 G z G z R z C z G z = = 可见,两个环节间有采样器隔开时,则环节串联等效脉冲传递函数为两个环节的脉 冲传递函数的乘积。同理, n 个环节串联,且所有环节之间均有采样器隔开时,则 等效脉冲传递函数为所有环节的脉冲传递函数的乘积。即 ( ) ( ) ( ) ( ) 1 2 G z G z G z G z n = (7-8)

c*(1) r0r*(2 G(s) 404 G,(s)c() 一G() (2)串联环节间无采样器时 如图7一3(b)所示,由于环节间没有采样器,因而G,(S)环节输入的信号不 是脉冲序列,而是连续函数,所以不能象图7-3(a)那样求G2()=C(e)/U1(e), 而应先把G(s)、G,(s)进行串联运算求出等效环节G,(s)G,(s),则G,(s)G,(s) 的:变换才是R()、C()之间的脉冲传递函数。即 Ge)-cQ-zG.wc.-G.c,) (7-9) R() 式中G,G2(:)表示G(S)G,(s)乘积经采样后的z变换。显然 ZG(s)G,(s)=GG,()G)G,() (7-10) 即各环节传递函数乘积的z变换,不等于各环节传递函数?变换的乘积。 c*) r(t)/r*() 41(1) G(s) G2(s) c() G() 由此可知,两个串联环节间无采样器隔开时,则等效脉冲传递函数等于两个环 节传递函数乘积经采样后的z变换。同理,此结论也使用于多个环节串联而无采样 器隔开的情况,即有 G()=ZG(s)G2(s)G(s)=GG2G() (7-11) 如果串联的多个环节中存在上述两种情况,则分段按上述原则处理。 如果把离散后的传递函数或变量记为G*(),则可以把上述两种情况简单归纳 110
110 (2) 串联环节间无采样器时 如图 7-3(b)所示,由于环节间没有采样器,因而 ( ) 2 G s 环节输入的信号不 是脉冲序列,而是连续函数,所以不能象图 7-3(a)那样求 ( ) ( ) ( ) 2 1 G z = C z U z , 而应先把 ( ) 1 G s 、 ( ) 2 G s 进行串联运算求出等效环节 ( ) ( ) 1 2 G s G s ,则 ( ) ( ) 1 2 G s G s 的 z 变换才是 R(z)、C(z) 之间的脉冲传递函数。即 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 Z G s G s G G z R z C z G z = = = (7-9) 式中 ( ) 1 2 G G z 表示 ( ) ( ) 1 2 G s G s 乘积经采样后的 z 变换。显然 ( ) ( ) ( ) ( ) ( ) 1 2 1 2 1 2 Z G s G s = G G z G z G z (7-10) 即各环节传递函数乘积的 z 变换,不等于各环节传递函数 z 变换的乘积。 由此可知,两个串联环节间无采样器隔开时,则等效脉冲传递函数等于两个环 节传递函数乘积经采样后的 z 变换。同理,此结论也使用于多个环节串联而无采样 器隔开的情况,即有 ( ) ( ) ( ) ( ) ( ) 1 2 1 2 G z Z G s G s G s G G G z = n = n (7-11) 如果串联的多个环节中存在上述两种情况,则分段按上述原则处理。 如果把离散后的传递函数或变量记为 G * (s) ,则可以把上述两种情况简单归纳 ( ) 1 G s ( ) 2 G s *( ) 1 ( ) u t 1 u t c(t) c * (t) ( ) 1 G z ( ) 2 G z r(t) r * (t) ( ) 1 G s ( ) 2 G s ( ) 1 u t c(t) c * (t) G (z) r(t) r * (t)
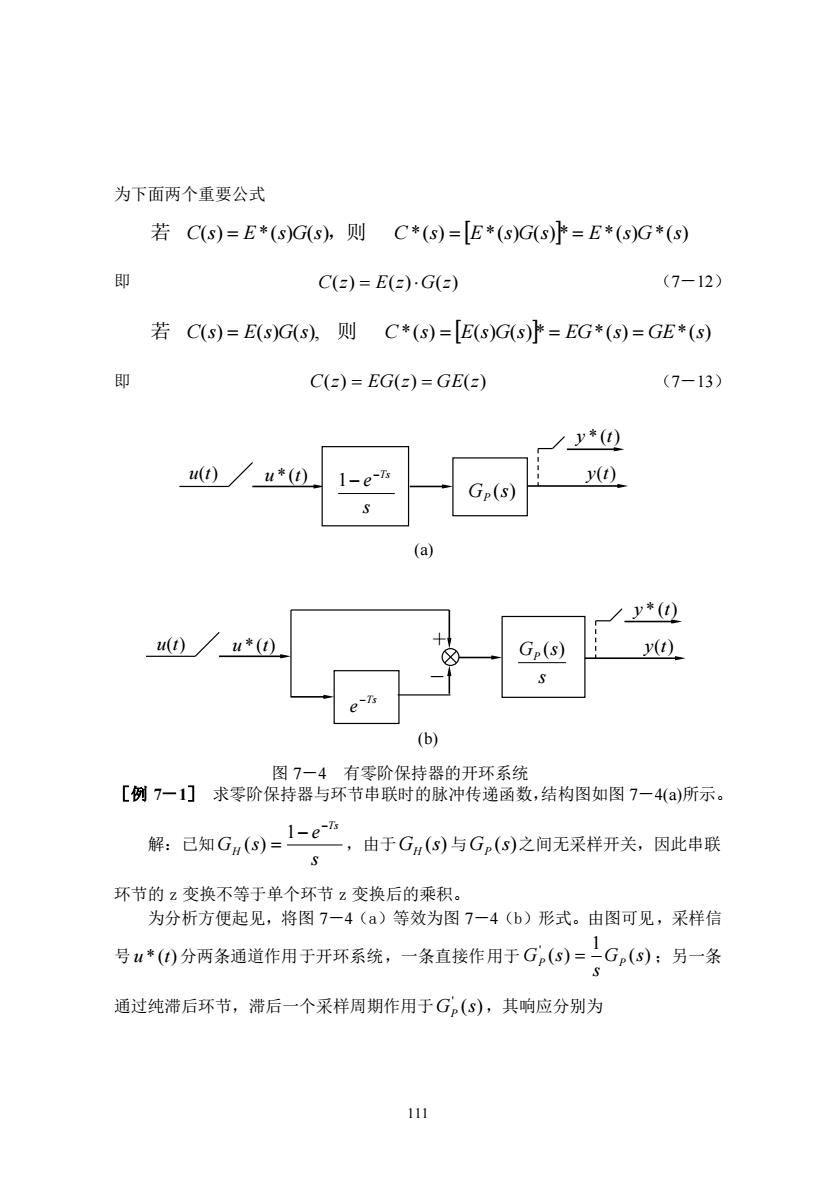
为下面两个重要公式 C(s)=E*(s)G(s),C*(s)=E*(s)G(s)=E*(s)G*(s) C()=E()G() (7-12) C(s)=E(s)G(s).C*(s)=E(s)G(s)=EG*(s)=GE*(s) C()=EG()=GE() (7-13) /y*@ 1-e- y(t) Gp(s) (a) /y*() G(s) y(t) e-k (b) 图7一4有零阶保持器的开环系统 [例7一1]求零阶保持器与环节串联时的脉冲传递函数,结构图如图7一4()所示。 解:已知Gn)=1-e” ,由于G(s)与G。(s)之间无采样开关,因此串联 环节的z变换不等于单个环节z变换后的乘积。 为分析方便起见,将图7-4(a)等效为图7-4(b)形式。由图可见,采样信 号1*(0分两条通道作用于开环系统,一条直接作用于G,(⊙)=上G,(S):另一条 通过纯滞后环节,滞后一个采样周期作用于G(),其响应分别为 111
111 为下面两个重要公式 若 C(s) = E*(s)G(s),则 C*(s) = E*(s)G(s)* = E*(s)G*(s) 即 C(z) = E(z)G(z) (7-12) 若 C(s) = E(s)G(s), 则 C*(s) = E(s)G(s)* = EG*(s) = GE*(s) 即 C(z) = EG(z) = GE(z) (7-13) [例 7-1] 求零阶保持器与环节串联时的脉冲传递函数,结构图如图 7-4(a)所示。 解:已知 s e G s Ts H − − = 1 ( ) ,由于 G (s) H 与 G (s) P 之间无采样开关,因此串联 环节的 z 变换不等于单个环节 z 变换后的乘积。 为分析方便起见,将图 7-4(a)等效为图 7-4(b)形式。由图可见,采样信 号 u *(t) 分两条通道作用于开环系统,一条直接作用于 ( ) 1 ( ) ' G s s G s P = P ;另一条 通过纯滞后环节,滞后一个采样周期作用于 ( ) ' G s P ,其响应分别为 s e −Ts 1− G (s) P u(t) u *(t) y(t) y * (t) (a) Ts e − s G s P ( ) y(t) y * (t) u(t) u *(t) + - (b) 图 7-4 有零阶保持器的开环系统

xe-G.ewe-zs.ove ge=cee)=99e 所以 Y(e)=Y(e)-Y2(e)=(1-:)Gp(e)U(e) 最后求得开环脉冲传递函数为 a得] Ls」 (7-50) 3.闭环脉冲传递函数 虽然离散控制系统的结构不变,由于采样开关的位置不同,对应的闭环脉冲传 递函数也不同。因此,这类系统的闭环传递函数没有一般计算公式。对于比较复杂 的离散控制系统,其闭环脉冲传递函数的计算将是十分复杂和困难的。 求取步骤:根据系统的结构写出各变量之间的关系式,利用两个重要结论,消 去中间变量,求出系统输出量的z变换表达式。如果R(2)单独存在,则可进一步求 出系统的闭环脉冲传递函数。 比较常见的一种离散控制系统的结构形式如图7-5所示,其闭环脉冲传递函数 为: C() GG2() R()1+GG,H() 式中,G,G2H()=ZG(s)G2(s)H(s】 H(S) G,G2()=ZIG,(s)G2(s】 其中G,G,H()为系统的开环脉冲传递函数。 7-5典型离散控制系统的结构图 当G,(s),G2(s)之间有采样开关存在,则 图7-5变换为图7-6,其闭环脉冲传递函数 og0ya回-X-G回9吧 为: C() G(E)G2(E) H(s) R()1+G()G,H() 式中,G2H()=Z1G2(s)H(s] 7-6典型离散控制系统的结构图 12
112 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 ' 1 2 ' 1 U z s G s Y z z G z U z z Z U z s G s Y z G z U z Z P P P P = = = = − − 所以 ( ) ( ) ( ) (1 ) ( ) ( ) 1 ' 1 2 ' 2 Y z Y z Y z z G z U z P − = − = − 最后求得开环脉冲传递函数为 − = = s G s Z z z U z Y z G z P 1 ( ) ( ) ( ) ( ) (7-50) 3.闭环脉冲传递函数 虽然离散控制系统的结构不变,由于采样开关的位置不同,对应的闭环脉冲传 递函数也不同。因此,这类系统的闭环传递函数没有一般计算公式。对于比较复杂 的离散控制系统,其闭环脉冲传递函数的计算将是十分复杂和困难的。 求取步骤:根据系统的结构写出各变量之间的关系式,利用两个重要结论,消 去中间变量,求出系统输出量的 z 变换表达式。如果 R(z)单独存在,则可进一步求 出系统的闭环脉冲传递函数。 比较常见的一种离散控制系统的结构形式如图 7-5 所示,其闭环脉冲传递函数 为: 1 ( ) ( ) ( ) ( ) 1 2 1 2 G G H z G G z R z C z + = 式中, ( ) [ ( ) ( ) ( )] 1 2 1 2 G G H z = Z G s G s H s ( ) [ ( ) ( )] 1 2 1 2 G G z = Z G s G s 其中 ( ) 1 2 G G H z 为系统的开环脉冲传递函数。 7-5 典型离散控制系统的结构图 当 ( ), ( ) 1 2 G s G s 之间有采样开关存在,则 图 7-5 变换为图 7-6 ,其闭环脉冲传递函数 为: 1 ( ) ( ) ( ) ( ) ( ) ( ) 1 2 1 2 G z G H z G z G z R z C z + = 式中, ( ) [ ( ) ( )] 2 2 G H z = Ζ G s H s 7-6 典型离散控制系统的结构图 ( ) 1 G s H(s) R(s) T E(s) C(s) ( ) 2 G s ( ) 1 G s H(s) R(s) T E(s) ( ) 2 G s C(s)

7.5离散控制系统的性能分析 与线性定常连续控制系统一样,线性定常离散控制系统也有稳定性、瞬态响应 和稳态误差等性能指标。 1离散系统的稳定性 离散系统稳定的充分必要条件是:系统的闭环极点均在:平面上以原点为中心 的单位圆内。即<1i=12,.m。 因此,可以通过求解闭环特征方程式的根来判断离散系统的稳定性。但当系统 的阶次较高或有待定常数时,采用此法不太合适,可以通过双线性变换 w-1 将:平面上的单位圆内部分映射到W平面的左半平面,即可使用劳斯稳定判据判断 离散系统的稳定性。 Im 7-7s平面与z平面的映射关系 2.稳态误差 单位反馈的离散系统(即图7-5中H(S)=1)的的稳态误差为 co)=lm(-0+G白 R(=) 其中G(:)=G,G,()为开环脉冲传递函数,通常选用三种典型输入信号,即单 位阶跃信号、单位斜坡信号和单位抛物线信号,对应R()变换分别为 T T2(e+1) -02-9 典型例题分析: 例7-2已知系统如图7-8所示,试分析系统E(X一kC) 的稳定性。 5(s+1) 解:解题的关键是根据己知条件求出离散控 制系统的特征方程(即闭环脉冲传递函数的分 113
113 7.5 离散控制系统的性能分析 与线性定常连续控制系统一样,线性定常离散控制系统也有稳定性、瞬态响应 和稳态误差等性能指标。 1.离散系统的稳定性 离散系统稳定的充分必要条件是:系统的闭环极点均在 z 平面上以原点为中心 的单位圆内。即 z 1 (i 1, 2, n) i = 。 因此,可以通过求解闭环特征方程式的根来判断离散系统的稳定性。但当系统 的阶次较高或有待定常数时,采用此法不太合适,可以通过双线性变换 1 1 − + = w w z 将 z 平面上的单位圆内部分映射到 w 平面的左半平面,即可使用劳斯稳定判据判断 离散系统的稳定性。 7-7 s 平面与 z 平面的映射关系 2.稳态误差 单位反馈的离散系统(即图 7-5 中 H(s) = 1 )的的稳态误差为 1 ( ) ( ) ( ) lim ( 1) 1 G z R z e z z + = − → 其中 ( ) ( ) 1 2 G z = G G z 为开环脉冲传递函数,通常选用三种典型输入信号,即单 位阶跃信号、单位斜坡信号和单位抛物线信号,对应 R(z) 变换分别为 3 2 2 2( 1) ( 1) , ( 1) , 1 − + − − z T z z z Tz z z 典型例题分析: [例 7-2]已知系统如图 7-8 所示,试分析系统 的稳定性。 解:解题的关键是根据已知条件求出离散控 制系统的特征方程(即闭环脉冲传递函数的分 s(s +1) R(s) K T =1s E(s) C(s) Re j Im 0 [S] 0 [Z]

母)。 图7-8离散控制系统 由图7-8可知,系统的开环脉冲传递函数为: K K1-e7) G=ZG)-Z片s+e-We7 其闭环脉冲传递函数为 C(=)_G(=) R(E)1+G(E) 则其特征方程为1+G(e)=0,(仁-1(:-eT)+K(l-eT)=0 因为T=1s,所以e1=0.368 1.当K1时代入上式并整理得 2-0.736:+0.368=0,52=-0.368±j0.482 由于52=V0.3682+0.4822=0.6071,所以系统是不稳定的。 3.下面分析稳定时K的取值范用 将:=”+!代入特征方程为仁-1WE-e-T)+K1-e1)=0 e-1 整理得 0.632Kw2+1.264w+(2.736-0.632K)=0 列劳斯表: w2 0.632K 2.736-0.632K 1264 w02.736-0.632K 为使系统稳定,要求劳斯表中第一列的系数均大于零,于是有 00时总是稳定的。有 了采样器后,系统稳定时K的范围就有了限制,加大K会导致系统不稳定。通常, 减小采样周期T,使系统工作尽可能接近于相应的连续系统,那么增益K的取值花 围可以加大。 [例7-3]试确定例7-5中系统对于单位阶跃输入、单位斜坡输入和单位抛物线输 入时的稳态误差。 解:解题的关键是根据已知条件求出开环脉冲传递函数, 系统的开环脉冲传递函数为: l-e-) G()=ZIG(s】= (e-10e-e7) 114
114 母)。 图 7-8 离散控制系统 由图 7-8 可知,系统的开环脉冲传递函数为: ( 1)( ) (1 ) ( 1) 1 ( ) [ ( )] T T z z e Kz e s K s K s s K G z G s − − − − − = + = − + = Z = Z Z 其闭环脉冲传递函数为 1 ( ) ( ) ( ) ( ) G z G z R z C z + = 则其特征方程为 1+ ( ) = 0, ( −1)( − ) + (1− ) = 0 −T −T G z z z e Kz e 因为 T=1 s,所以 0.368 1 = − e 1.当 K=1 时代入上式并整理得 0.736 0.368 0, 1,2 0.368 0.482 2 z − z + = z = − j 由于 0.368 0.482 0.607 1 2 2 z1,2 = + = ,所以系统是稳定的。 2.当 K=5 时,特征方程为 1.792 0.368 0, 1 0.237 2 1.555 2 z + z + = z = − z = − 由于 z2 =1.555 1 ,所以系统是不稳定的。 3.下面分析稳定时 K 的取值范围 将 1 1 − + = w w z 代入特征方程为 ( −1)( − ) + (1− ) = 0 −T −T z z e Kz e 整理得 0.632 1.264 (2.736 0.632 ) 0 2 Kw + w+ − K = 列劳斯表: w K w w K K 2.736 0.632 1.264 0.632 2.736 0.632 0 1 2 − − 为使系统稳定,要求劳斯表中第一列的系数均大于零,于是有 0 K 4.32 可以看出,当系统中没有采样器时,二阶连续系统在 K 0 时总是稳定的。有 了采样器后,系统稳定时 K 的范围就有了限制,加大 K 会导致系统不稳定。通常, 减小采样周期 T ,使系统工作尽可能接近于相应的连续系统,那么增益 K 的取值范 围可以加大。 [例 7-3]试确定例 7-5 中系统对于单位阶跃输入、单位斜坡输入和单位抛物线输 入时的稳态误差。 解:解题的关键是根据已知条件求出开环脉冲传递函数。 系统的开环脉冲传递函数为: ( 1)( ) (1 ) ( ) [ ( )] T T z z e Kz e G z Z G s − − − − − = =