新疆大学：《自动控制理论》课程教学资源（教案讲义）第三章 时域分析法

第三章控制系统的时域分析法 丝析和设计系统的首要工作是确定系统的数学模器 。一旦建立了合理的、便于分析的数 ，就可以对已组成的控制系统进行分析，从而得出系统性能的改进方法。 经典控制理论中，常用时域分析法、根轨迹法或频率分析法来分析控制系统的性能。本 章介绍的时与 “是通过传递函数、拉氏变换及反变换求出系统在典型输入下的输出表达 R(s) 式，从而分析 间向应的全部信息。与其他分析法出较，时域分析法是一种直接分析法 具有直观和准确的优点，尤其适用于 二阶系统性能的分析和计算。对二阶以上的高阶系 统则须采用频率分析法和根轨迹法 3.1典型输入信号 控制系统的输出响应是系统数学模型的解。系统的输出响应不仅取决于系统本身的结 盈软数，初找盗品都食入信S的形式省初险状态以作梦一定。如现定为E边 为统 的形式 响应由系 身的结 数米确员 因而更便于对各种系统进行比较和研究。自动控制系统常用的典型输入信号有如图3一1所 示几种形式： 名称 曲线 时域表达式 复域表达式 r(t) R10120 阶跃函数 R=1单位阶跃函数 nt) 611≥0 斜坡函到 h=】单位斜坡函数 n(t) 加速度函数 120 单位加速度函数 r(t) 801-0 脉冲函数 6u) 单位理相歌冲函数 r(t) 正弦函数 Asinox 图31典型输入信号 3.2一阶系统的时域响应 凡是可用一阶微分方程描述的系统称一阶系统。 一阶系统的传递函数为 G6)=Ts+1 式中T称为时间常数，它是表征系统惯性的一个重要参数。所以一阶系统是一个非周期的 惯性环 下面分析在单位阶跃响应三种不同的典型输入信号作用下一阶系统的时域分析 R(s) 1C(s) Ts 19

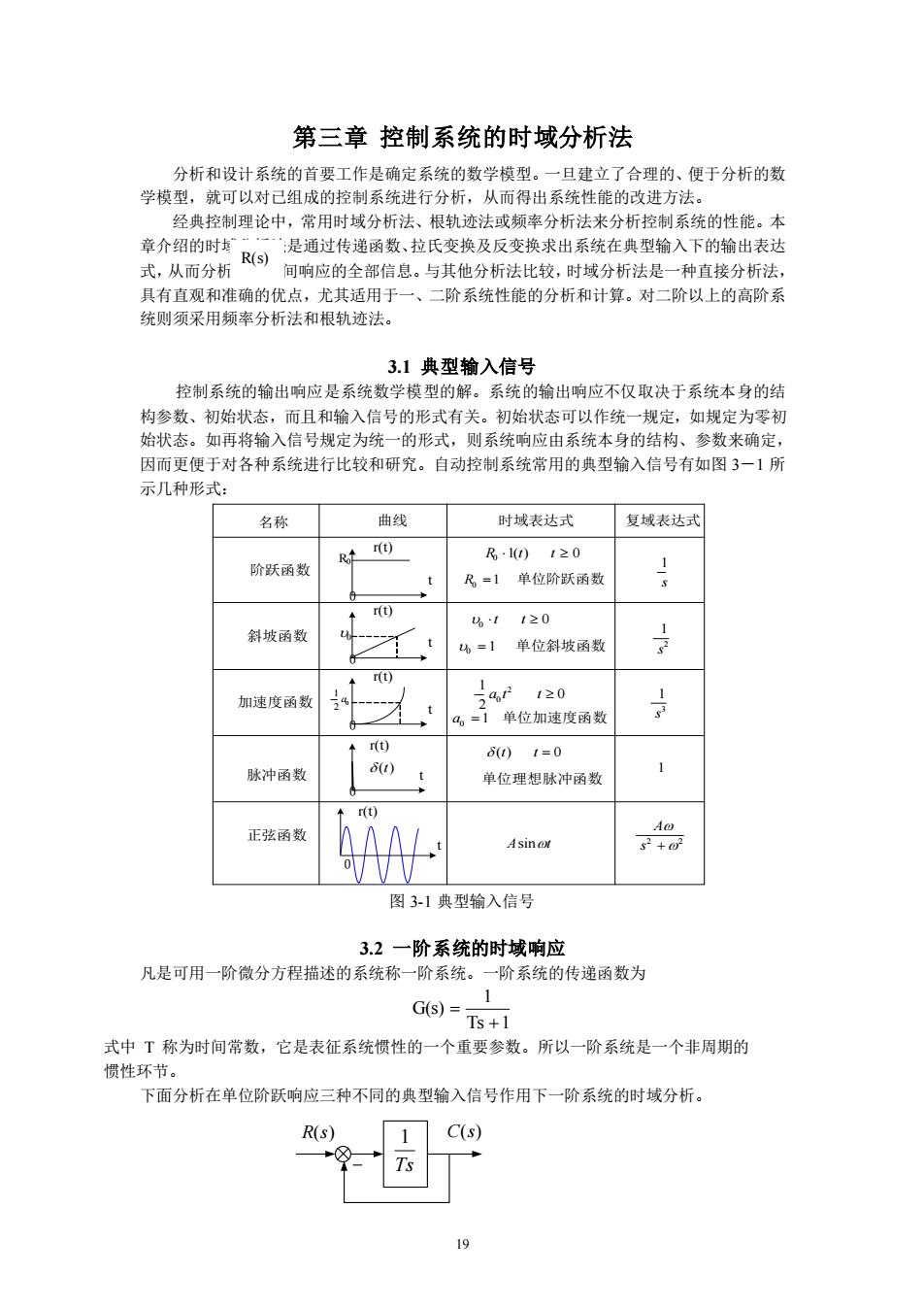
19 第三章 控制系统的时域分析法 分析和设计系统的首要工作是确定系统的数学模型。一旦建立了合理的、便于分析的数 学模型，就可以对已组成的控制系统进行分析，从而得出系统性能的改进方法。 经典控制理论中，常用时域分析法、根轨迹法或频率分析法来分析控制系统的性能。本 章介绍的时域分析法是通过传递函数、拉氏变换及反变换求出系统在典型输入下的输出表达 式，从而分析系统时间响应的全部信息。与其他分析法比较，时域分析法是一种直接分析法， 具有直观和准确的优点，尤其适用于一、二阶系统性能的分析和计算。对二阶以上的高阶系 统则须采用频率分析法和根轨迹法。 3.1 典型输入信号 控制系统的输出响应是系统数学模型的解。系统的输出响应不仅取决于系统本身的结 构参数、初始状态，而且和输入信号的形式有关。初始状态可以作统一规定，如规定为零初 始状态。如再将输入信号规定为统一的形式，则系统响应由系统本身的结构、参数来确定， 因而更便于对各种系统进行比较和研究。自动控制系统常用的典型输入信号有如图 3－1 所 示几种形式： 名称 阶跃函数 斜坡函数 加速度函数 脉冲函数 正弦函数 曲线 时域表达式 复域表达式 ０ t r(t) ０ t r(t) ０ t r(t) R0 0 ０ t r(t) 0 2 1 a  (t) R0 1(t) t  0 0 t t  0 0 2 1 2 a0 t t   (t) t  0 Asint R0 1 单位阶跃函数 0  1 单位斜坡函数 a0  1 单位加速度函数 单位理想脉冲函数 s 1 2 1 s 3 1 s 1 2 2   s  A ０ t r(t) 图 3-1 典型输入信号 3.2 一阶系统的时域响应 凡是可用一阶微分方程描述的系统称一阶系统。一阶系统的传递函数为 Ts 1 1 G(s)   下面分析在单位阶跃响应三种不同的典型输入信号作用下一阶系统的时域分析。 式中 T 称为时间常数，它是表征系统惯性的一个重要参数。所以一阶系统是一个非周期的 惯性环节。 R(s) Ts 1 R(s) C(s)

当输入信号r)=1()时，Rs=1s,系统输出量的拉氏变换为 cs)=s+)s+1 对上式取拉氏反变换，得单位阶跃响应为 c0-1-e7 (t≥0) 由此可见，一阶系统的阶跃响应是一条初始值为0，按指数规律上升到稳态值1的曲线， 如图32所示。由系统的输出响应可得到如下的性能。 (1)由于c)的终值为1，因此系统稳态误差为0。 T时，-0632。这表明当系统的单位阶跃响应达到稳态值的63.2%时的时间。 单位阶跃响应曲线的初始斜率为 这表明一阶系统的单位阶跃响应如果以初始速度上升到稳态值1，所需的时间恰好等于 =1 e-w 图32一阶系统的时域响应 (3)根据暂态性能指标的定义可以求得 调节时间为 t.=3Ts+5%的提差带 t.=4T(s) (士2%的误差带) 延迟时间为 t4=0.69T(s) 上升时间为 t,=2.20T(s) 峰值时间和超调量都为0。 3.3二阶系统的阶跃响应 凡是可用二阶微分方程描写的系统称为二阶系统。 在工程实我中 阶系统不乏其例 特别是，不少高阶系统在一定条件下可用二阶系统的特性来近似表征。因此，研究典型二阶 系统的分析和计算方法，具有较大的实际意义。 3.3.1二阶系统的数学模型 典型的二阶系统动态结构图如图，系统的开环传递函数为 K R(s) C(s) G)=s5+Ds6+20,】 (Ts+D 系统的闭环传递函数为

20 当输入信号 r(t)=1(t)时，R(s)=1/s，系统输出量的拉氏变换为 1 1 s(Ts 1) 1 c(s)   −   TS T s 对上式取拉氏反变换，得单位阶跃响应为 c(t)  1− (  0) − e t T t 由此可见，一阶系统的阶跃响应是一条初始值为 0，按指数规律上升到稳态值 1 的曲线， 如图 3-2 所示。由系统的输出响应可得到如下的性能。 (1)由于 c(t)的终值为 1，因此系统稳态误差为 0。 (2)当 t=T 时，c(T)=0.632。这表明当系统的单位阶跃响应达到稳态值的 63.2%时的时间， 就是该系统的时间常数 T。 单位阶跃响应曲线的初始斜率为 T e T t T t t 1 1 dt dc(t) 0 0    −  这表明一阶系统的单位阶跃响应如果以初始速度上升到稳态值 1，所需的时间恰好等于 T。 图 3-2 一阶系统的时域响应 (3)根据暂态性能指标的定义可以求得 调节时间为 ts =3T(s) (±5%的误差带) ts =4T(s) (±2%的误差带) 延迟时间为 td =0.69T(s) 上升时间为 tr =2.20T(s) 峰值时间和超调量都为 0。 3.3 二阶系统的阶跃响应 凡是可用二阶微分方程描写的系统称为二阶系统。在工程实践中，二阶系统不乏其例; 特别是，不少高阶系统在一定条件下可用二阶系统的特性来近似表征。因此，研究典型二阶 系统的分析和计算 方法，具有较大的实际意义。 3.3.1 二阶系统的数学模型 典型的二阶系统动态结构图如图，系统的开环传递函数为 ( 1) ( 2 ) ( ) 2 n n s Ts s s K G s       系统的闭环传递函数为 0 0.632 T C(t) t T c t e / ( ) 1 −  − 0 0.632 T t C(t) 1 t T t e / ( ) 1 −  − 0.95 3T R(s) s(Ts1) K C(s)

C(s)K R72+5+K2+2G,3+ 其中5为典型二阶系统的阻尼比（或相对阻尼比），©为无阻尼振荡频率或称自然振荡 角频率。系统闭环传递函数的分母等于零所得方程式称为系统的特征方程式。典型二阶系统 的特征方程式为 s2+2∠0n3+0n2=0 它的两个特征根是512=-0n±0。V2-1 当01，称为过阻尼状态。特征根为两个不相等的负实根。 当50，称为无阻尼状态。特征根为一对纯虚根。 和@。是二阶系统两个重要参数，系统响应特性完全由这两个参数来描述。 3.3.2二阶系统的时域响应 下面分几种情况来分析二阶系统的暂态特性。 (1)欠阻尼情况(0<<1) 由于0<5<1，则系统的一对共轭复数根可写为 s12=-0n±j0V1-5 当输入信号为单位阶跃函数时，系统输出量的拉氏变换为 G8-+2+欧对 =+a+++a 3+50n 式中0：=0V一S2。对上式进行拉氏反变换，则欠阻尼二阶系统的单位阶跃响应为 0=1-ems-Fou+2hi-Gon ,+0 =1-1 式中 sinB=1-5.cosB=5

21 2 2 2 2 ( ) 2 ( ) n n n Ts s K s s K R s C s          其中  为典型二阶系统的阻尼比（或相对阻尼比），n 为无阻尼振荡频率或称自然振荡 角频率。系统闭环传递函数的分母等于零所得方程式称为系统的特征方程式。典型二阶系统 的特征方程式为 s 2 0 2 2  n s n  它的两个特征根是 s 1 2 1,2  −n n  − 当 01，称为过阻尼状态。特征根为两个不相等的负实根。 当  =0，称为无阻尼状态。特征根为一对纯虚根。  和n 是二阶系统两个重要参数，系统响应特性完全由这两个参数来描述。 3.3.2 二阶系统的时域响应 下面分几种情况来分析二阶系统的暂态特性。 （1）欠阻尼情况（0<  <1） 由于 0<  <1，则系统的一对共轭复数根可写为 2 s1,2  −n  jn 1− 当输入信号为单位阶跃函数时，系统输出量的拉氏变换为 2 2 2 2 2 2 2 ( ) ( ) 1 1 s 2 s (s) n d n n d n n n n s s s s s C            −     −     式中 2  d   n 1− 。对上式进行拉氏反变换，则欠阻尼二阶系统的单位阶跃响应为 sin( ) ( 0) 1 1 1 sin 1 ) 1 (t) 1 (cos 1 2 2 2 2   −  − − −  − −  − − e t t c e t t d t n n t n n            式中 2 sin  1− , cos  

B-arctan -arccos 由上式知欠阻尼二阶系统的单位阶跃响应由两部分组成，第一项为稳态分量，第二项为 暂态分量。它是一个幅值按指数规律衰减的有阻尼的正弦振荡，振荡角频率为®。·响应曲 线如图所示。 (2)临界阻尼情况(5=1) 当5=1时，系统有两个相等的负实根，为 512=0。 在单位阶跃函数作用下，输出量的拉氏变换为 C(s)(s+0)3+0 其反拉氏变换为 c0=1-ew1+o) (u20) 上式表明，临界阻尼二阶系统的单位阶跃响应是稳态值为1的非周期上升过程，整个响 应特性不产生振荡。响应曲线如图所示。 (3)过阻尼情况(5>1) 当>1时，系统有两个不相等的负实根 s2=-5o,±oV2-i 当输入信号为单位阶跃函数时，输出量的拉氏变换为： qo-。- 其反变换为 1 e-e 0=12-+ge司≥0 上式表明，系统响应含有两个单调衰减的指数项，它们的代数和决不会超过稳态值1，因而 过阻尼二阶系统的单位阶跃响应是非振荡的。响应曲线如图33所示。 (4)无阻尼情况(5-0) 当5-0时输出量的拉氏变换为

22     arccos 1 arctan 2  −  由上式知欠阻尼二阶系统的单位阶跃响应由两部分组成，第一项为稳态分量，第二项为 暂态分量。它是一个幅值按指数规律衰减的有阻尼的正弦振荡，振荡角频率为  d 。响应曲 线如图所示。 （2）临界阻尼情况（  =1） 当  =1 时，系统有两个相等的负实根，为 1,2   n s 在单位阶跃函数作用下，输出量的拉氏变换为 n n n n n n s s s s s s C s        −   −    1 ( ) 1 ( 2 ) ( ) 2 2 2 2 其反拉氏变换为 ( )  1− (1 ) (  0) − c t e t t n t n   上式表明，临界阻尼二阶系统的单位阶跃响应是稳态值为 1 的非周期上升过程，整个响 应特性不产生振荡。响应曲线如图所示。 （3）过阻尼情况（  >1） 当>1 时，系统有两个不相等的负实根 s 1 2 1,2  −n n  − 当输入信号为单位阶跃函数时，输出量的拉氏变换为： s s s C n 1 (s -s )( ) (s) 1 2 2  −   其反变换为 ] 1 1 [ 2 1 1 (t) 1 2 ( 1) 2 ( 1) 2 2 2 2 2  − − − − −  − − − − −  −         t    t n n e e c 上式表明，系统响应含有两个单调衰减的指数项，它们的代数和决不会超过稳态值 1，因而 过阻尼二阶系统的单位阶跃响应是非振荡的。响应曲线如图 3-3 所示。 （4）无阻尼情况（  =0） 当  =0 时输出量的拉氏变换为 （t≥0）

C(s)= s(s"+o) 特征方程式的根为 S12=-j0 因此二阶系统的输出响应为 C(t)=1-cos@! (t≥0】 上式表明，系统为不衰减的振荡，其振荡频率为@ di) 系统属不稳定系统。 综上所述，可以看出，在不同阻尼比时， 二阶系统的闭环极点和暂态响应有很大区别。阻尼 =1.0 比5为二阶系统的重要特征参量。当5=0时，系统不能 2。 正常工作，而在(>1时，系统暂态响应又进行得太慢， 所以，对二阶系统来说，欠阻尼情况是最有意义的， 图3-3二阶系统单位阶跃响应 下面讨论这种情况下的暂态特性指标。 3.3.3二阶系统阶跃响应的性能指标 典型二阶系统单位耽跃响应如图34所示。 c(co) tt 图34典型二阶系统单位阶跃响应 延迟时间指输出响应第一次达到稳态值50%所需的时间。 上升时间 指输出响应从稳态值的10%上升到90%所需的时间。对有振荡的系统 则取响应从零到第一次达到稳态值所需的时间。 峰值时间指输出响应超过稳态值而达到第一个峰值（即c()所需的时间。 调节时间t。指当输出量c0)和稳态值c(∞)之间的偏差达到允许范围（一般取2%或 5%)以后不再超过此值所需的最短时间。 最大超调量（或称超调量）M 指暂态过程中输出响应的最大值超过稳态值的百分 数。即 M,%=t,小-coj ×100% c(oo)

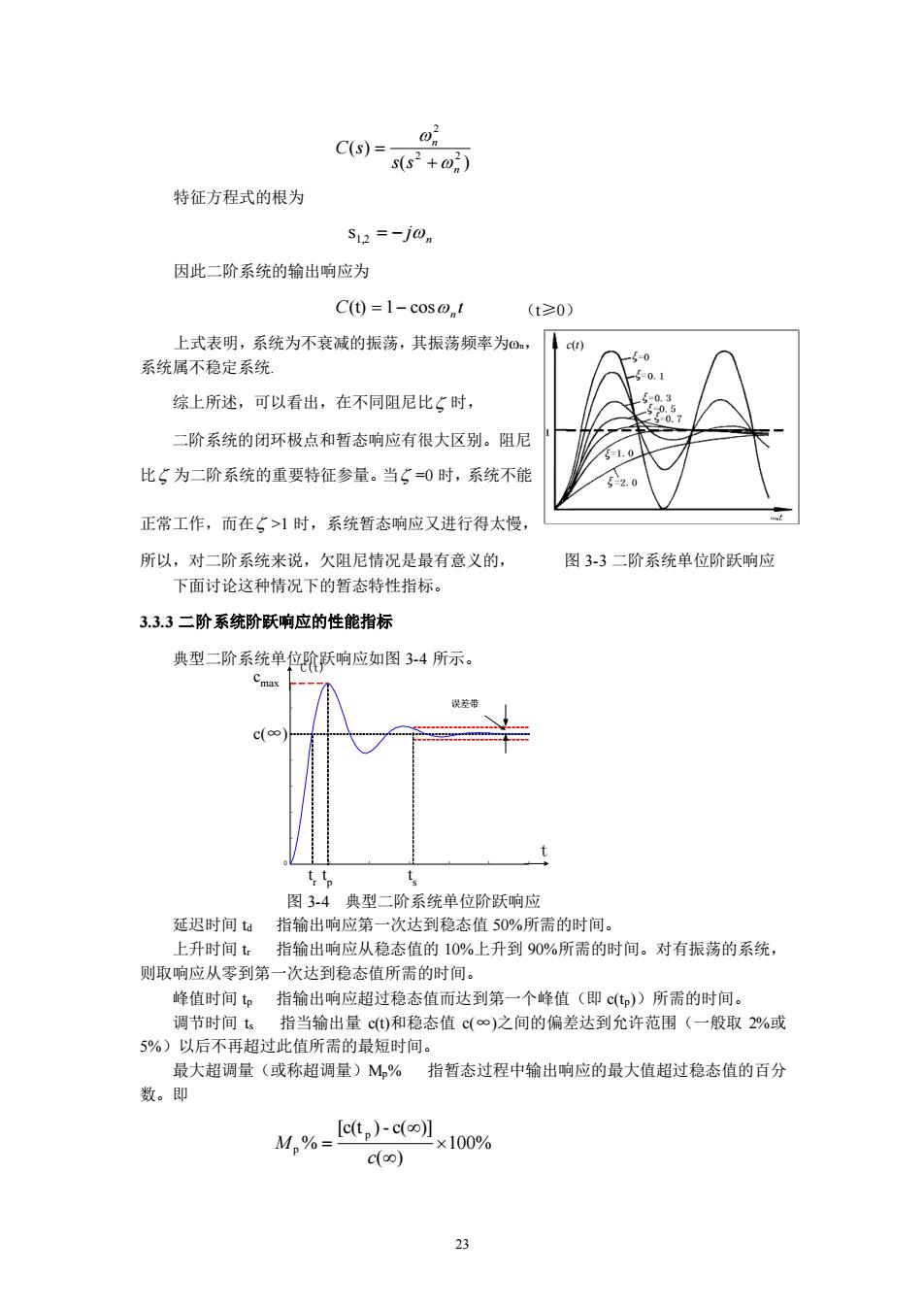
23 ( ) ( ) 2 2 2 n n s s C s     特征方程式的根为 n s1,2  − j 因此二阶系统的输出响应为 C t n (t)  1− cos 上式表明，系统为不衰减的振荡，其振荡频率为n， 系统属不稳定系统. 综上所述，可以看出，在不同阻尼比  时， 二阶系统的闭环极点和暂态响应有很大区别。阻尼 比  为二阶系统的重要特征参量。当  =0 时，系统不能 正常工作，而在  >1 时，系统暂态响应又进行得太慢， 所以，对二阶系统来说，欠阻尼情况是最有意义的， 图 3-3 二阶系统单位阶跃响应 下面讨论这种情况下的暂态特性指标。 3.3.3 二阶系统阶跃响应的性能指标 典型二阶系统单位阶跃响应如图 3-4 所示。 图 3-4 典型二阶系统单位阶跃响应 延迟时间 td 指输出响应第一次达到稳态值 50%所需的时间。 上升时间 tr 指输出响应从稳态值的 10%上升到 90%所需的时间。对有振荡的系统， 则取响应从零到第一次达到稳态值所需的时间。 峰值时间 tp 指输出响应超过稳态值而达到第一个峰值（即 c(tp)）所需的时间。 调节时间 ts 指当输出量 c(t)和稳态值 c(∞)之间的偏差达到允许范围（一般取 2%或 5%）以后不再超过此值所需的最短时间。 最大超调量（或称超调量）Mp% 指暂态过程中输出响应的最大值超过稳态值的百分 数。即 100% ( ) [c(t ) - c( )] % p p     c M （t≥0） c(t) 0 误差带 t C(t) c(∞) cmax t r t p t s

稳态误差C,指系统输出实际值与希望值之差。 在上述几项指标中，峰值时间p、上升时间和延迟时间u均表征系统响应初始阶段的 快慢：调节时间表征系统过渡过程（暂态过程）的持续时间，从总体上反映了系统的快速 性：而超调量M,%标志暂态过程的稳定性：稳态误差反映系统复现输入信号的最终精度。 上升时间 根据定义，当=时，0)=1 1 yt,)=1- sndo)=1 则 -存esmo6+m=0 由于 g*0e40 1 所以有 al+B= 于是上升时间 i=(r-B)/o对 显然，增大或减小5，均能减小，从而加快系统的初始响应速度。 峰值时间G 将式c)对时间t求导，并令其为零，可求得峰值时间即 to) 因为 IgB=- 0p-0,2 被峰自时涧定义，它对应大超调量，即0第一次出现蜂值所对应的时间么所以应取 π (t≥0) 上式说明，峰值时间恰好等于阻尼振荡周期的一半，当一定时极点距实轴越远，越 最大超调量L% 当tp时，c)有最大值ct)m,即c)m=ctp。对于单位阶跃输入，系统的稳态值c(∞Fl, 得最大输出为

24 稳态误差 ess 指系统输出实际值与希望值之差。 在上述几项指标中，峰值时间 tp、上升时间 tr和延迟时间 td 均表征系统响应初始阶段的 快慢；调节时间 ts 表征系统过渡过程（暂态过程）的持续时间，从总体上反映了系统的快速 性；而超调量 Mp%标志暂态过程的稳定性；稳态误差反映系统复现输入信号的最终精度。 上升时间 tr 根据定义，当 t=tr 时，y(tr)=1 sin( ) 1 1 1 (t ) 1 2 r   −  − −     d r t y e t n r 则 sin( ) 0 1 1 2   − −     d r t e t n r 由于 0, 0 1 1 2   − − n r t e   所以有 dtr +β=π 于是上升时间 tr=（π-β）/d 显然，增大n 或减小  ，均能减小 tr，从而加快系统的初始响应速度。 峰值时间 tp 将式 c(t)对时间 t 求导，并令其为零，可求得峰值时间 tp，即 [ sin( ) cos( )] 0 1 (t) 1 2 −     −   − − −          d p t d p d t p n t t e t e t dt dc n p n p 从而 得     2 1 ( ) − tg d t p   因为    2 1− tg  从而得 dtp=0, π,2π,. 按峰值时间定义，它对应最大超调量，即 c(t)第一次出现峰值所对应的时间 tp,所以应取 n d p t      2 1−   上式说明，峰值时间恰好等于阻尼振荡周期的一半，当一定时极点距实轴越远，tp 越 小。 最大超调量 Mp% 当 t=tp 时,c(t)有最大值 c(t)max,即 c(t)max= c(tp)。对于单位阶跃输入，系统的稳态值 c(∞)=1， 得最大输出为 （t≥0）

c(t)mx =c(tp)=1- -sx+网 因为 s(π+B)=-snB=-G月 所以 d(l)=1+e 则超调量为 M%=ex100% 可见超调量仅由5决定，越大，%越小。 调节时间5 根据调节时间的定义，应由下式求出 m4,+osA c=c∞)-c0=e9 由上式可看出，求解上式十分困难。由于正弦函数存在，：值与5间的函数关系是不 连续的，为了简便起见，可采用近似的计算方法，忽略正弦函数的影响，认为指数函数衰减 到△=-0.05或△=0.02时，暂态过程即进行完毕。这样得到 e- -=A 即 1 -n△V1-52) 由此求得 aB-1-61 3 1(5%)= 1,(2%)= 通过以上分析可知，近似与5@成反比。在设计系统时，（通常由要求的最大超调量 决定，所以调节时间，由无阻尼自然振荡频率@所决定。也就是说，在不改变超调量的条件 下，通过改变@值米改变调节时间

25 sin( ) 1 (t) ( ) 1 2 1 max 2       −   − − − e c c t p 因为 2 sin(  )  −sin   − 1− 所以 2 1 ( ) 1   − − c t   e p 则超调量为 % 100% 2 1   − −   M p e 可见超调量仅由  决定,  越大，p%越小。 调节时间 ts 根据调节时间的定义, ts 应由下式求出    −    −  − sin( ) 1 ( ) ( ) 2     d s t t e c c c t n s 由上式可看出，求解上式十分困难。由于正弦函数存在，ts 值与  间的函数关系是不 连续的，为了简便起见，可采用近似的计算方法，忽略正弦函数的影响，认为指数函数衰减 到Δ=0.05 或Δ=0.02 时，暂态过程即进行完毕。这样得到 y e n s t   − − 2 1   即 ln( 1 ) 1 2    −  − n s t 由此求得 n n s t    3 ln(1 )] 2 1 [3 1 (5%) 2  − −  n n s t    4 ln(1 )] 2 1 [4 1 (2%) 2  − −  通过以上分析可知，ts 近似与  n 成反比。在设计系统时，  通常由要求的最大超调量 决定，所以调节时间 ts 由无阻尼自然振荡频率n 所决定。也就是说，在不改变超调量的条件 下，通过改变n 值来改变调节时间 ts

例31】已知单位反馈随动系统如图3-5所 示.若K=16,T=025s.试求 R(s) (1)典型二阶系统的特征参数5和0，： (2)动态性能指标M,和1，(5%： (3)欲使M。=16%,当T不变时，K应取何值。 图3-5随动系统结构图 解：[题意分析]这是一道典型二阶系统求性能指标的练习题。关键是要抓住二阶系 统闭环传递函数的标准形式与特征参数5和®，的对应关系，然后由对应公式去求性能指 标。 [解题步瓓 1.由系统结构图可求出闭环系统的传递函数为 C(s) 人 K/T 2。与典型=阶系统传递函数的标准形式9 02 `R回s2+2505+进行比较，可知： 52KT 己知K、T值，由上式可得 16 0n=K=o=8ad1s.g=2,/702 1 3.由性能指标计算公式，可以求出： M,6-e高×100%=e器x10%-4% 3 3 1. 0,025x8=1.54=5%0 4为使M,=166.由公式M,%=e六×10w%可求府 5= [n M]2 [n0.162 -hM示“h8可=05 即应使5由0.25增大到0.5，此时由 1 1 1 5=2K 可以求出K 474x025x05=4 即K值应由16减小到4，即诚小了4倍。 【例32！设二阶控制系统的单位阶跃响应c()↑ 曲线如图3-6所示。如果该系统为单位反馈控 1.2 制系统，试确定其开环传递函数及闭环传递函 1 数· 解：[题意分析]这是一道由性能指标反求 二阶系统的参数5和⊙的题目。关健是①由 单位阶跃响应曲线求出M,和1。，②由M。 1,求出5和0n,③根据5和on, 图3-6单位阶跃响应曲线

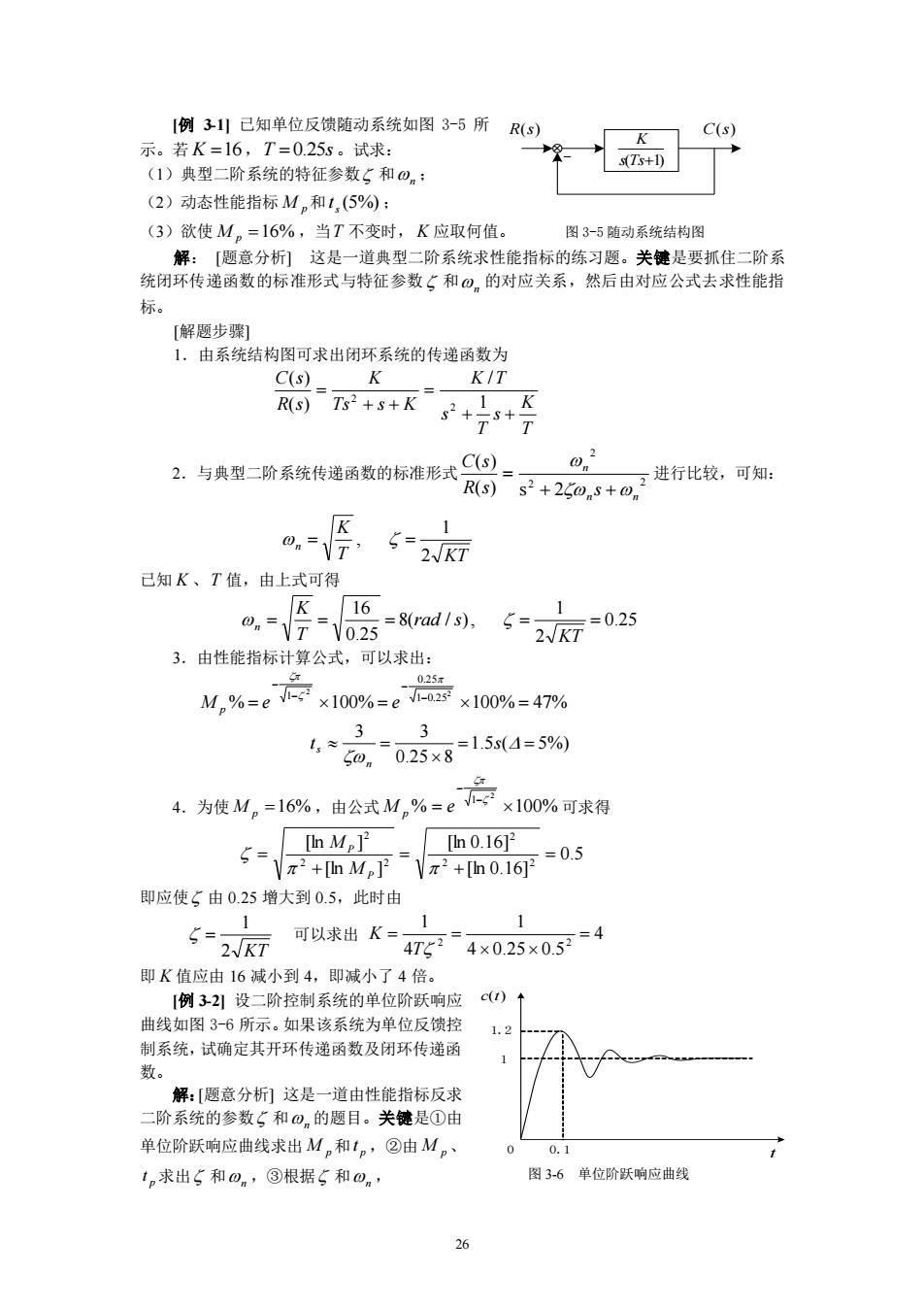
26 [例 3-1] 已知单位反馈随动系统如图 3-5 所 示。若 K 16，T  0.25s 。试求： （1）典型二阶系统的特征参数  和 n ； （2）动态性能指标 M p 和 (5%) s t ； （3）欲使 M p 16% ，当 T 不变时， K 应取何值。 图 3-5 随动系统结构图 解： [题意分析] 这是一道典型二阶系统求性能指标的练习题。关键是要抓住二阶系 统闭环传递函数的标准形式与特征参数  和 n 的对应关系，然后由对应公式去求性能指 标。 [解题步骤] 1．由系统结构图可求出闭环系统的传递函数为 T K s T s K T Ts s K K R s C s       1 / ( ) ( ) 2 2 2．与典型二阶系统传递函数的标准形式 2 2 2 ( ) s 2 ( ) n n n R s s C s       进行比较，可知： T KT K n 2 1   ,   已知 K 、T 值，由上式可得 0.25 2 1 8( / ), 0.25 16      KT rad s T K n  3．由性能指标计算公式，可以求出： % 100% 100% 47% 2 2 1 0.25 0.25 1      − − − −    M e e p 1.5 ( 5%) 0.25 8 3 3        t s n s 4．为使 M p 16% ，由公式 % 100% 2 1   − −   M e p 可求得 0.5 [ln 0.16] [ln 0.16] [ln ] [ln ] 2 2 2 2 2 2         P P M M 即应使  由 0.25 增大到 0.5，此时由 2 KT 1   可以求出 4 4 0.25 0.5 1 4 1 2 2      T K 即 K 值应由 16 减小到 4，即减小了 4 倍。 [例 3-2] 设二阶控制系统的单位阶跃响应 曲线如图 3-6 所示。如果该系统为单位反馈控 制系统，试确定其开环传递函数及闭环传递函 数。 解：[题意分析] 这是一道由性能指标反求 二阶系统的参数  和 n 的题目。关键是①由 单位阶跃响应曲线求出 M p 和 p t ，②由 M p 、 p t 求出  和 n ，③根据  和 n ， R(s) s(Ts1) K C(s) 0 0.1 1 1.2 c(t) t 图 3-6 单位阶跃响应曲线

写出典型二阶系统的开环传递函数及闭环传递函数。 [解题步骤 1.由图35可知本例题系统为欠阻尼系统，可以从上图直接得出： M,=12-1×10%=20%,1,=0.15 1 2.由M,%=e高×10%=20% 可以解得：5= [h0.22 云2+hM,了r+h02T=0456 0= =35.3rad/s 1v1-5 3.系统开环传递函数为： G(s)= 1246.1 s+260n)5(s+32.2 闭环传递函数为：C 1246.1 +26@5++322s+1246 由以上讨论，可得到如下结论 女阻尼比5是二阶系统的重要参数，由5值的大小，可以间接判断一个二阶系统的暂 态品质。在过阻尼的情况下，暂态特性为单调变化曲线，没有超调量和振荡，但调节时间较 长，系统反应迟缓。当S≤0时输出量作等幅振荡或发散振荡，系统不能稳定工作。 女一般情况下，系统在欠阻尼情况下工作。但是5过小，则超调量大，振荡次数多， 调节时间长，暂态特性品质差。应该注意，超调量只和阻尼比有关。因此，通常可以根据允 许的超调量来选择阻尼比5。 女调节时间与系统阻尼比和这两个特征参数的乘积成反比。在阻尼比一定时，可 通过改变来改变暂态响应的持续时间。@越大，系统的调节时间越短。 ☆为了限制超调量，并使调节时间，较短，阻尼比一般在0.4~0.8之间，这时阶跃响 应的超调量将在25%~1.5%之间。 3.3.4.改善系统督态性能的方法： C(s ①在系统中加入比例微分环节 s+2.1 比例一微分控制的二阶系统如图36所示： T为微分器的时间常数。由图可见，系统输出量 同时受误差信号及其速率的双重作用 因而比例一微分控制是一种早期拉制， 图3-6比例-微分控制 可在出现位置误差前提前产生修正作用，从而达到改善系统性能的目的。 ②在系统中加入速度反馈环节

27 写出典型二阶系统的开环传递函数及闭环传递函数。 [解题步骤] 1．由图 3-5 可知本例题系统为欠阻尼系统，可以从上图直接得出： 100% 20% 1 1.2 1   − M p  ， t s p  0.1 2．由 % 100% 20% 2 1    − −   M e p 可以解得： 0.456 [ln 0.2] [ln 0.2] [ln ] [ln ] 2 2 2 2 2 2         P P M M rad s t p n 35.3 / 1 2  −     3．系统开环传递函数为： ( 32.2) 1246.1 ( 2 ) ( ) 2     s s s s G s n n   闭环传递函数为： 32.2 1246.1 1246.1 ( ) 2 ( ) 2 2 2 2       R s s s s s C s n n n    由以上讨论，可得到如下结论： ☆ 阻尼比  是二阶系统的重要参数，由  值的大小，可以间接判断一个二阶系统的暂 态品质。在过阻尼的情况下，暂态特性为单调变化曲线，没有超调量和振荡，但调节时间较 长，系统反应迟缓。当  ≤0 时输出量作等幅振荡或发散振荡，系统不能稳定工作。 ☆ 一般情况下，系统在欠阻尼情况下工作。但是  过小，则超调量大，振荡次数多， 调节时间长，暂态特性品质差。应该注意，超调量只和阻尼比有关。因此，通常可以根据允 许的超调量来选择阻尼比  。 ☆ 调节时间与系统阻尼比  和n 这两个特征参数的乘积成反比。在阻尼比一定时，可 通过改变n 来改变暂态响应的持续时间。n 越大，系统的调节时间越短。 ☆ 为了限制超调量，并使调节时间 ts 较短，阻尼比一般在 0.4～0.8 之间，这时阶跃响 应的超调量将在 25% ～ 1.5%之间。 3.3.4．改善系统暂态性能的方法： ①在系统中加入比例微分环节 比例—微分控制的二阶系统如图 3-6 所示： Td 为微分器的时间常数。由图可见，系统输出量 同时受误差信号及其速率的双重作用。 因而比例—微分控制是一种早期控制， 图 3-6 比例—微分控制 可在出现位置误差前提前产生修正作用，从而达到改善系统性能的目的。 ②在系统中加入速度反馈环节 R(s) ( 2 ) 2 n n s s    1  C(s) T sd E(s)

将输出的速度信号反馈到系统输入端，并与误差信号比较，同样可以增大阻尼比，改 善系统动态性能。如图3-7所示 以上两种方法都可以增大阻尼比(，减小超调量和调整时间。 29-+2」厂 C(s) 图3-7速度反馈控制 例3-3引控制系统框图如图3-8所示。要 求系统单位阶跃响应的超调量M。=9.5%, R(s) 10C(s) +-05s+ 且峰值时间1。=0.5s。试确定K与x的值， 可 并计算在此情况下系统上升时间·和调整 间1，(2%). 解：「题意分析这是一道由性能指标反求 图3-8控制系统框图 二阶系统的参数的愿目。关键是要找出：①K1、T与S和0n的关系，②M。、【,与5和 0n的关系，③以5和0n为桥梁米确定K1、t的值。 [解题步骤 1.由图3-6可得控制系统的闭环传递函数为： C(s) 20K, R()s2+(2+20r)5+20K 与典型二阶系统的传递函最C⊙ 2 ）S+20,5+包比较，可得 m,2=20K1,2n=2+20z 2.由题设条件 M。=eFx10%=0.095,1,= f05x 可解得：5=0.6,0=7.854 3.因此求得：K=%=308,r=2-2=037 20 34高阶系统的时域分析 设高阶系统的传递函数可表示为： 6)=6”+6s+b5+6 (n≥m) (3-23) dos"+ajs"+.as+a 设闭环传递函数的零点为-24，2，2a,极点为p1,p,Pa,则闭环传递函数可表示为 Y)=K+X6+6+) （(n2m) (s+ps+p2).(s+p) 当输入信号为单位阶跃信号时，输出信号为： 28

28 将输出的速度信号反馈到系统输入端，并与误差信号比较，同样可以增大阻尼比，改 善系统动态性能。如图 3-7 所示 以上两种方法都可以增大阻尼比  ，减小超调量和调整时间。 图 3-7 速度反馈控制 [例 3-3]控制系统框图如图 3-8 所示。要 求系统单位阶跃响应的超调量 M p  9.5% ， 且峰值时间 t s p  0.5 。试确定 K1 与  的值， 并计算在此情况下系统上升时间 r t 和调整时 间 (2%) s t 。 解：[题意分析] 这是一道由性能指标反求 图 3-8 控制系统框图 二阶系统的参数的题目。关键是要找出：① K1 、 与  和 n 的关系，② M p 、 p t 与  和 n 的关系，③以  和 n 为桥梁来确定 K1 、 的值。 [解题步骤] 1．由图 3-6 可得控制系统的闭环传递函数为： 1 2 1 (2 20 ) 20 20 ( ) ( ) s s K K R s C s      与典型二阶系统的传递函数 2 2 2 ( ) s 2 ( ) n n n R s s C s       比较，可得  20 , 2 2 20 1 2 n  K n   2．由题设条件： 100% 0.095 2 1    − − M e p ，t s n p 0.5 1 2  −     可解得：   0.6, n  7.854 3．因此求得： 0.37 20 2 2 3.08, 20 2 1  −    n n K    3.4 高阶系统的时域分析 设高阶系统的传递函数可表示为： ( ) . . ( ) 1 1 0 1 1 1 0 1 n m a s a s a s a b s b s b s b s n n n n m m m m         − − − −  设闭环传递函数的零点为-z1,-z2,.,-zm，极点为-p1,-p2,., -pn，则闭环传递函数可表示为： ( ) ( )( ).( ) ( )( ).( ) ( ) 1 2 1 2 n m s p s p s p K s z s z s z Y s n m         当输入信号为单位阶跃信号时，输出信号为： ( 2 ) 2 n n s s    C(s) K sT R(s) E(s) K1 R(s) C(s)  s (0.5 1) 10 s s  （3-23）