《电路》课程参考书籍（ELCTRIC CIRCUIT）CAPTER 6 SINUSOIDSAND PHASORS

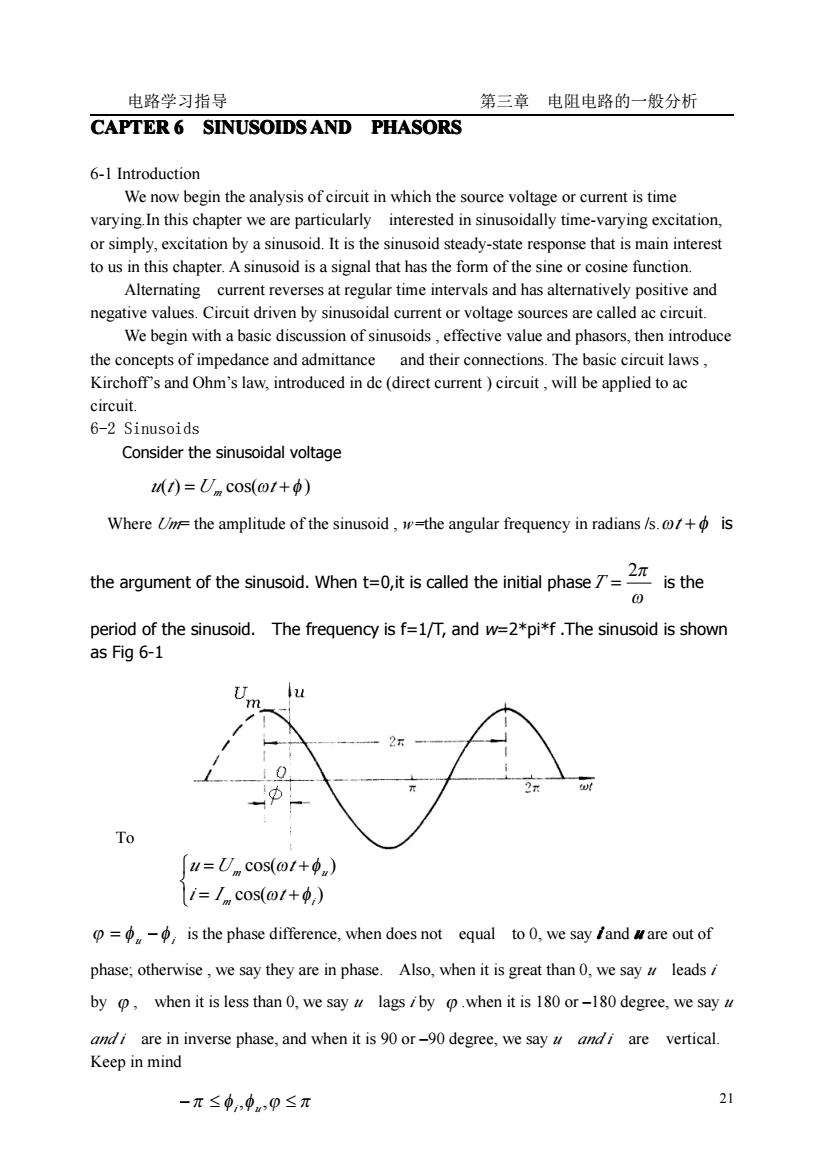
电路学习指导 第三章电阻电路的一般分析 CAPTER6 SINUSOIDSAND PHASORS 6-1 Introduction We now begin the analysis of circuit in which the source voltage or current is time varying. In this chapter we are particularly interested in sinusoidally time-varying excitation, or simply, excitation by a sinusoid. It is the sinusoid steady-state response that is main interest to us in this chapter. A sinusoid is a signal that has the form of the sine or cosine function. Alternating current reverses at regular time intervals and has alternatively positive and negative values. Circuit driven by sinusoidal current or voltage sources are called ac circuit. We begin with a basic discussion of sinusoids, effective value and phasors, then introduce the concepts of impedance and admittance and their connections. The basic circuit laws, Kirchoff's and Ohm's law, introduced in de (direct current ) circuit, will be applied to ac circuit. 6-2 Sinusoids Consider the sinusoidal voltage u(1)=Umcos(1+φ) Where Um=the amplitude of the sinusoid, w=the angular frequency in radians /s. o+ is the argument of the siusoid.When tex iti s allete initial phase-In is the period of the sinusoid. The frequency is f=1/T, and w=2*pi*f. The sinusoid is shown as Fig 6-1 U u m 2元 0 —# π 2元 wl To u=Umcos(1+φn) i=Imcos(o1+φ) p=u-o,is the phase difference,when does not equal to 0,we say /and ware out of phase; otherwise, we say they are in phase. Also, when it is great than 0， we say leads / by o,when it is less than O,we say u lagsiby o.when it is 180 or-180 degree,we say u and i are in inverse phase, and when it is 90 or-90 degree, we say u and i are vertical. Keep in mind -丌≤,,甲≤丌 21

电路学习指导 第三章 电阻电路的一般分析 21 CAPTER 6 SINUSOIDS SINUSOIDS SINUSOIDS SINUSOIDS AND PHASORS PHASORS PHASORS PHASORS 6-1 Introduction We now begin the analysis of circuit in which the source voltage or current is time varying.In this chapter we are particularly interested in sinusoidally time-varying excitation, or simply, excitation by a sinusoid. It is the sinusoid steady-state response that is main interest to us in this chapter. A sinusoid is a signal that has the form of the sine or cosine function. Alternating current reverses at regular time intervals and has alternatively positive and negative values. Circuit driven by sinusoidal current or voltage sources are called ac circuit. We begin with a basic discussion of sinusoids , effective value and phasors, then introduce the concepts of impedance and admittance and their connections. The basic circuit laws , Kirchoff’s and Ohm’s law, introduced in dc (direct current ) circuit , will be applied to ac circuit. 6-2 Sinusoids Consider the sinusoidal voltage Where Um= the amplitude of the sinusoid , w=the angular frequency in radians /s.ωt +φ is the argument of the sinusoid. When t=0,it is called the initial phase ω 2π T = is the period of the sinusoid. The frequency is f=1/T, and w=2*pi*f .The sinusoid is shown as Fig 6-1 Fig.6-1 To ϕ = φ u −φ i is the phase difference, when does not equal to 0, we say i and u are out of phase; otherwise , we say they are in phase. Also, when it is great than 0, we say u leads i by ϕ , when it is less than 0, we say u lags i by ϕ .when it is 180 or –180 degree, we say u and i are in inverse phase, and when it is 90 or –90 degree, we say u and i are vertical. Keep in mind u(t) =U cos(ωt +φ ) m ⎩ ⎨ ⎧ = + = + cos( ) cos( ) m i m u i I t u U t ω φ ω φ −π ≤ φi,φu ,ϕ ≤ π

电路学习指导 第三章电阻电路的一般分析 A direct source applied to the resistor R in a period causes the energy is While a alterating current through the same resistor in a period causes the energy is Tf they are equal,I is called the effective value ofi 75 1= 6-4 Complex number 1 Rectangular form 法m✉ 个+ =rZ=e 中■ Wherer is the magnitude is the phase or angle. =行些玩，产与得张) x=rcoso,y=rsind ∴.z=cosp+/sino), triangleform Complex number operations Addition and subtractionParallelogram Triangle 以边运电 MultiplicationSquare root E=F∠A Reciprocal

电路学习指导 第三章 电阻电路的一般分析 22 A direct source applied to the resistor R in a period causes the energy is RI T 2 While a alternating current through the same resistor in a period causes the energy is ∫ T Ri dt 0 2 Tf they are equal , I is called the effective value of i. 6-4 Complex number 1 Rectangular form x is the real part, y is the imaginary part 2 Polar or exponential form Where r is the magnitude ϕ is the phase or angle. Vector (shown as Fig.6-2) Complex Complex Complex Complex number operations operations operations operations1 Addition and subtractionParallelogram Triangle Fig.6-3 Fig.6-4 Division MultiplicationSquare root Reciprocal ∫ = T i dt T I 0 1 2 ⎪ ⎩ ⎪ ⎨ ⎧ = = 2 2 m m I I U U z = x + jy, j = −1 φ φ j z = r∠ = re ( ) ( ) 1 2 1 2 1 2 z ± z = x ± x + j y ± y 1 2 2 1 2 1 = ∠φ −φ r r z z 1 2 = 1 2∠φ1 +φ2 z z rr 2 φ z = r∠ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ∴ = + = = = + = − triangleform z r j x r y r x y r x y tg (cos sin ), cos , sin , 2 2 1 φ φ φ φ φ

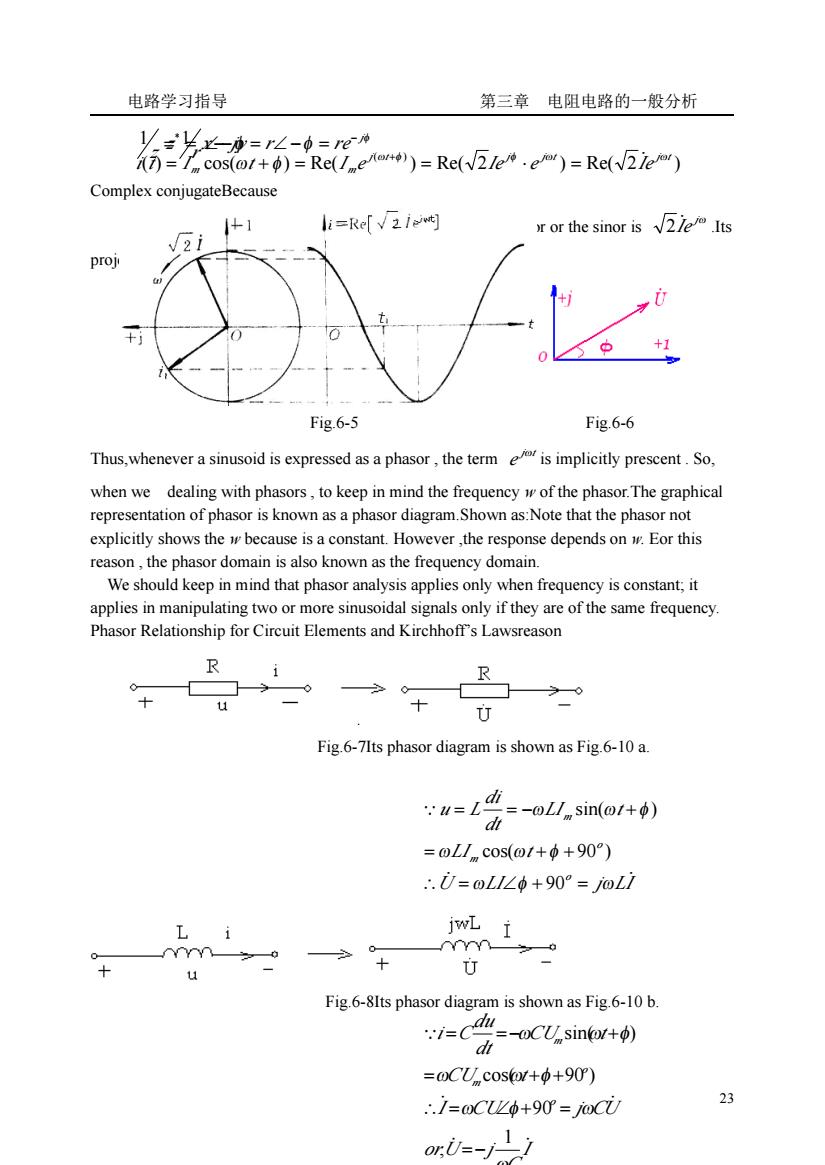
电路学习指导 第三章电阻电路的一般分析 养步62-Rmi=Raw5 Complex conjugateBecause 从1 li=Rel2u] or or the sinor is Its i proj Fig.6-5 Fig.6-6 Thus,whenever a sinusoid is expressed as a phasor,the termis implicitly prescent.So. when we dealing with phasors,to keep in mind the frequencyof the phasor.The graphical representation of phasor is known as a phasor diagram.Shown as:Note that the phasor not explicitly shows thebecause is a constant.However the response dependsonEor this reason,the phasor domain is also known as the frequency domain We should keep in mind that phasor analysis applies only when frequency is constant;it applies in manipulating two or more sinusoidal signals only if they are of the same frequency. Phasor Relationship for Circuit Elements and Kirchhoffs Lawsreason R + u U Fig 6-7Its phasor diagram is shown as Fig6-10 a. =-@L/sin(@/+6) =oL/cos(++90) .0=oL1∠中+90°=oLi L i 三 u Fig.6-8Its phasor diagram is shown as Fig.6-10 b. =-@CUsin+) =OCUcost+6+90) ∴1=0CL0+90=0CU ori=-111

电路学习指导 第三章 电阻电路的一般分析 23 Complex conjugateBecause φ φ I = Ie = I∠ j ̇ is the representation of i(t),The rotate phasor or the sinor is jω Iė 2 .Its projection on the real axis is i(t) Fig.6-5 Fig.6-6 Thus,whenever a sinusoid is expressed as a phasor , the term j t e ω is implicitly prescent . So, when we dealing with phasors , to keep in mind the frequency w of the phasor.The graphical representation of phasor is known as a phasor diagram.Shown as:Note that the phasor not explicitly shows the w because is a constant. However ,the response depends on w. Eor this reason , the phasor domain is also known as the frequency domain. We should keep in mind that phasor analysis applies only when frequency is constant; it applies in manipulating two or more sinusoidal signals only if they are of the same frequency. Phasor Relationship for Circuit Elements and Kirchhoff’s Lawsreason Fig.6-7Its phasor diagram is shown as Fig.6-10 a. Fig.6-8Its phasor diagram is shown as Fig.6-10 b. = ∠−φ z r 1 1 φ φ j z x jy r re − = − = ∠− = * ( ) cos( ) Re( ) Re( 2 ) Re( 2 ) j( t ) j j t j t m m i t I t I e Ie e Ie ω φ φ ω ω ω φ = ̇ = + = = ⋅ + U LI j LI LI t LI t dt di u L o o m m ̇ ̇ ∵ ω φ ω ω ω φ ω ω φ ∴ = ∠ + = = + + = = − + 90 cos( 90 ) sin( ) I C orU j I CU j CU CU t CU t dt du i C o o m m ̇ ̇ ̇ ̇ ∵ ω ω φ ω ω ω φ ω ω φ 1 , 90 cos( 90 ) sin( ) =− ∴ = ∠ + = = + + = =− +

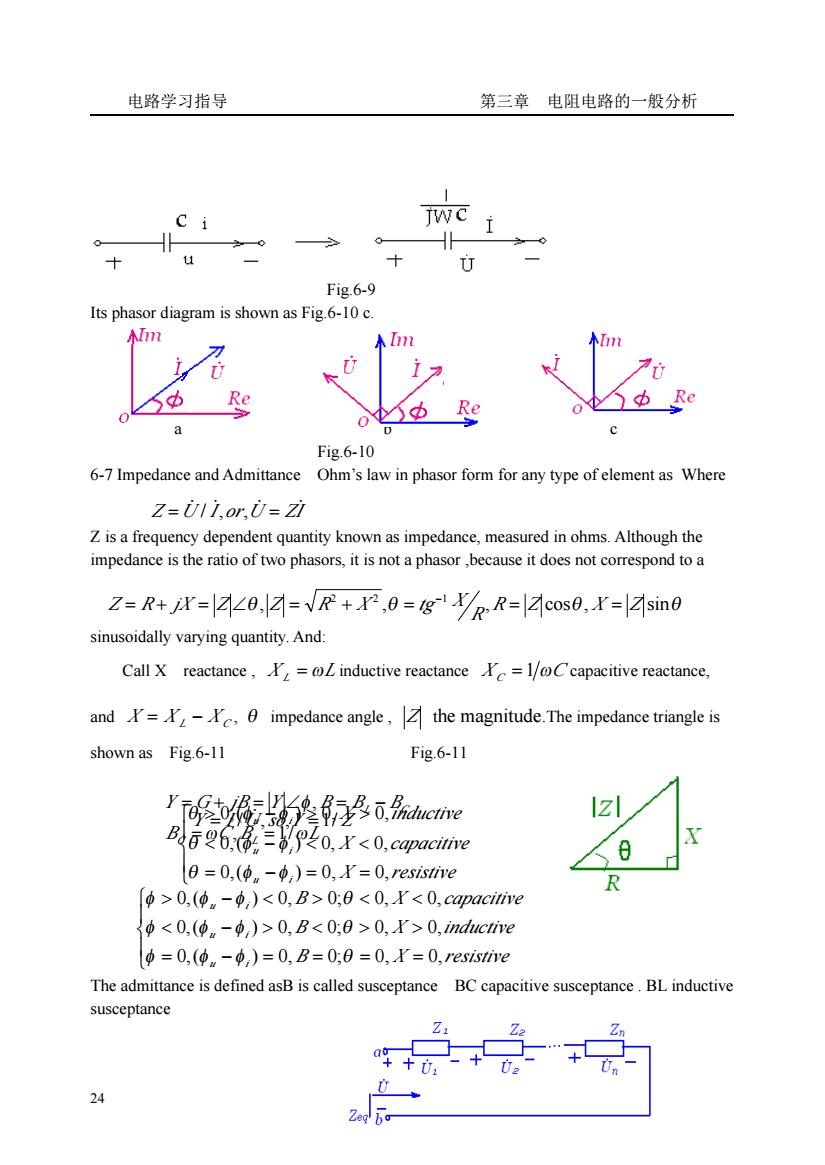
电路学习指导 第三章电阻电路的一般分析 wC i 0 H 11 Fig.6-9 Its phasor diagram is shown as Fig.6-10 c. m 刀 i a 电型 Fig.6-10 6-7 Impedance and Admittance Ohm's law in phasor form for any type ofelement as Where Z=ili.or.i=zt Z is a frequency dependent quantity known as impedance,measured in ohms.Although the impedance is the ratio of two phasors,it is not a phasor,because it does not correspond to a Z=R+X=∠0，A=√R+r,0=g'R=cos0,r=sin0 sinusoidally varying quantity.And: Call X reactance,=oL inductive reactance =l/Ccapacitive reactance, and=-c.0 impedance angle,the magnitude.The impedance triangle is shown as Fig.6-11 Fig.6-11 12 :.x0,(p.-p,)0:80,B0,r>0,inductive p=0,(pn-p,)=0,B=0,0=0,r=0,resistive The admittance is defined asB is called susceptance BC capacitive susceptance.BL inductive susceptance

电路学习指导 第三章 电阻电路的一般分析 24 Fig.6-9 Its phasor diagram is shown as Fig.6-10 c. a b c Fig.6-10 6-7 Impedance and Admittance Ohm’s law in phasor form for any type of element as Where Z is a frequency dependent quantity known as impedance, measured in ohms. Although the impedance is the ratio of two phasors, it is not a phasor ,because it does not correspond to a sinusoidally varying quantity. And: Call X reactance , X L = ωL inductive reactance X C = 1 ωC capacitive reactance, and X = X L − X C , θ impedance angle , Z the magnitude.The impedance triangle is shown as Fig.6-11 Fig.6-11 The admittance is defined asB is called susceptance BC capacitive susceptance . BL inductive susceptance Z U I or U ZI = ̇ ̇ ̇ = ̇ / , , θ , ,θ , cosθ, sinθ 2 2 1 R Z X Z R Z = R + jX = Z ∠ Z = R + X = tg X = = − ⎪ ⎩ ⎪ ⎨ ⎧ = − = = − > > X resistive X capacitive X inductive u i u i u i 0,( ) 0, 0, 0,( ) 0, 0, 0,( ) 0, 0, θ φ φ θ φ φ θ φ φ Y = I ̇ /U̇ ,so,Y =1/ Z B C B L Y G jB Y B B B C L L C ω ω φ , 1/ , = = = + = ∠ = − ⎪ ⎩ ⎪ ⎨ ⎧ = − = = = = > > − < < B X resistive B X inductive B X capacitive u i u i u i 0,( ) 0, 0; 0, 0, 0,( ) 0, 0; 0, 0, 0,( ) 0, 0; 0, 0, φ φ φ θ φ φ φ θ φ φ φ θ

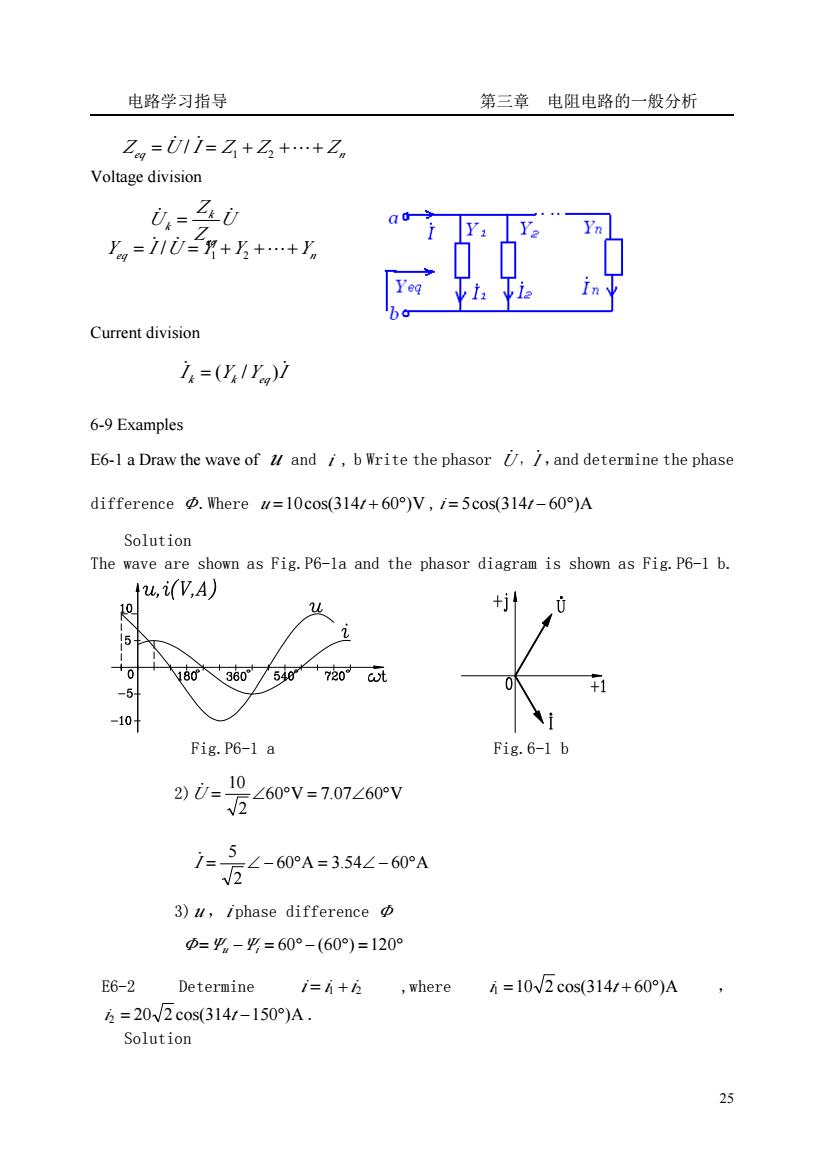
电路学习指导 第三章电阻电路的一般分析 Z=011=Z+Z3+.+Z。 Voltage division 0-三d Y. Yn =11U=月+乃+.+ Current division i=(y1y)1 6-9 Examples E6-1 a Draw the wave of and i,b Write the phasor /and determine the phase difference Where w=10cos(314/+60)V,/=5cos(314/-60)A Solution The wave are shown as Fig.P6-la and the phasor diagram is shown as Fig.P6-1 b. ,(V,A) 10 1 036o/50+720 +1 -5 10 Fig.P6-1 a Fig.6-1 b <60V=707∠60V 2)0=-10 万-60A=3.54∠-60A 3)u,iphase difference =平-g=60°-(60)=120° E6-2 Determine i=i+乃 where =10W2c0s(3141+60)A 5=20√2cos(314/-150°)A. Solution 25

电路学习指导 第三章 电阻电路的一般分析 25 Voltage division Current division 6-9 Examples E6-1 a Draw the wave of u and i , b Write the phasor U̇ ， I ̇ ，and determine the phase difference Φ.Where u =10cos(314t + 60°)V , i = 5cos(314t − 60°)A Solution The wave are shown as Fig.P6-1a and the phasor diagram is shown as Fig.P6-1 b. Fig.P6-1 a Fig.6-1 b 2) 60 V 7.07 60 V 2 10 U = ∠ ° = ∠ ° ̇ 60 A 3.54 60 A 2 5 I = ∠ − ° = ∠ − ° ̇ 3) u ，i phase difference Φ Φ=Ψu −Ψi = 60° − (60°) =120° E6-2 Determine i = i1 + i2 ,where i1 =10 2 cos(314t + 60°)A ， i2 = 20 2 cos(314t −150°)A . Solution eq Z Z Zn Z =U̇ / I ̇ = 1 + 2 +⋯+ U Z Z U eq k k ̇ = ̇ eq U Y Y Yn Y = I ̇ / ̇ = 1 + 2 +⋯+ I Y Y I k k eq ̇ ̇ = ( / )

电路学习指导 第三章电阻电路的一般分析 Using phasor to calculate it /=10∠60°A,2=20∠-150°A 7=7+2=10∠60°A+20∠-150°A =(5+j8.66)A+(-17.32-j10)A =(-12.32-j1.34)A =12.39∠-173.8A ∴1=12.39V2cos(314r-173.8)A E6-3 The circuit is shown as Fig E6-3,the reading of A,is 5A,A,is 20A, As is 25A,determine the reading of A and Aa. Solution Because R,L and C are connected in parallel,we can assume (=(0V According to the relationship of voltage and current of R.L and C,we get 1=5∠0°A，=-j20A=20∠90°A,=j25A=25∠90°A KCL:4=2+3=-j20A+j25A=j5A=5∠90°A 1=i+14=i+2+2=5+j5A=7.07∠45A .'.so the reading of A is 7.07A,the reading of A is 5A. g104 L 43 RI ·① Fig.P6-3 Fig.6-4 E6-4 The circuit is shown as Fig E6-4,the reading of the voltage meters are: Vi:15V:V2:80V:V3:100V,determine the reading ofV. Solution Because R、L and C are connected in series,we can assume=∠0°A According to the relationship of voltage and current of R,L and C,we getU=15∠0V,2=80∠90V,0=100∠-90V KVL:i=+2+3=(15∠0°+80∠90°+100∠-90)V =15-20V=25∠-53.13V

电路学习指导 第三章 电阻电路的一般分析 26 Using phasor to calculate it I ̇ 1 =10∠60°A ， I ̇ 2 = 20∠ −150°A I ̇ = I ̇ 1 + I ̇ 2 =10∠60°A + 20∠ −150°A = (5 + j8.66)A + (−17.32 − j10)A = (−12.32 − j1.34)A =12.39∠ −173.8°A ∴i1 =12.39 2 cos(314t −173.8°)A E6-3 The circuit is shown as Fig E6-3, the reading of A1 is 5A ， A2 is 20A ， A3 is 25A , determine the reading of A and A4 . Solution Because R 、 L and C are connected in parallel，we can assume U̇ =U∠0°V According to the relationship of voltage and current of R 、 L and C , we get I ̇ 1 = 5∠0°A ， I ̇ 2 = −j20A = 20∠90°A , I ̇ 3 = j25A = 25∠90°A KCL ： I ̇ 4 = I ̇ 2 + I ̇ 3 = −j20A + j25A = j5A = 5∠90°A I ̇ = I ̇ 1 + I ̇ 4 = I ̇ 1 + I ̇ 2 + I ̇ 2 = 5 + j5A = 7.07∠45°A ∴so the reading of A is 7.07A，the reading of A4 is 5A . Fig.P6-3 Fig.6-4 E6-4 The circuit is shown as Fig E6-4, the reading of the voltage meters are: V1 ：15V ； V2 ：80V ；V3：100V , determine the reading ofV. Solution Because R 、 L and C are connected in series，we can assume I ̇ = I∠0°A According to the relationship of voltage and current of R 、 L and C , we get U̇ 1 =15∠0°V ，U̇ 2 = 80∠90°V ，U̇ 1 =100∠ − 90°V KVL：U̇ =U̇ 1 +U̇ 2 +U̇ 3 = (15∠0° + 80∠90° +100∠ − 90°)V =15 − j20V = 25∠ − 53.13°V

电路学习指导 第三章电阻电路的一般分析 The reading of the voltmeter V is 25V. E6-5 In the circuit Fig.E6-5),the angular frequency is the effective value of thecurrent is 1A,determine the effective value of the voltage U Fig.E6-5 Solution u=12+(2-3)2 x1=v E6-6 Determine the input impedance (Fig.E6-6,is known ) R ao- ao L3 bo (a) (b) Fig.E6-6 Solution a)a=R+8C*(6+jo (B+jo0x(B+o己 joC+(j) 1 (b)Z= 民+ja☑++C E6-6The circuit is shown as Fig.E6-7a,determine current iand the voltage phasor of each element,and draw the phasor diagram.Where R=150,L=12mH, C=5u F, M=100√2cos(50001)V +0R-+0 Solution i Uc 0=100∠0V,ZR=152,Z=joL=j602, 2e"mG-H0 Fig.E6-7 a Z=Z+Z+Z=15+j60-j40=15+j202 =25∠53.132 27

电路学习指导 第三章 电阻电路的一般分析 27 The reading of the voltmeter V is 25V . E6-5 In the circuit ( Fig .E6-5), the angular frequency isω, the effective value of thecurrent is 1A, determine the effective value of the voltage U. I 1Ω j2Ω -j3Ω U Fig.E6-5 Solution 2 2 u V = + − × = 1 (2 3) 1 2 E6-6 Determine the input impedance Zab (Fig.E6-6,ω is known ). (a) (b) Fig.E6-6 Solution (a) ( j ) j 1 ( j ) j 1 2 2 ab 1 R L C R L C Z R ω ω ω ω + + × + = + ；(b) ) j 1 ( j ) ( ) j 1 ( j ) ( 1 2 1 2 ab C R L R C R L R Z ω ω ω ω + + + + × + = E6-6The circuit is shown as Fig.E6-7a , determine current and the voltage phasor of each element, and draw the phasor diagram. Where R =15Ω ， L =12mH ， C = 5μ F ， u =100 2 cos(5000t)V . Solution U̇ =100∠0°V ， ZR =15Ω, Z L = jωL = j60Ω, = = −j40Ω j 1 C ZC ω Fig.E6-7 a Zeq = Z R + Z L + ZC =15 + j60 − j40 =15 + j20Ω = 25∠53.13°Ω

电路学习指导 第三章电阻电路的一般分析 7-010020° 石2525313=45313A 4+j R=Ri=60∠-53.13V d=joLi=240∠36.87V -53.13° +1 Uc tc=2=160c-14s13v So the phasor diagram is Fig.E6-7 b The sinusoid is /=42 cos(5000/-53.13)A E6-8In circuit shown as Fig.E6-8 a,R=50,R=22,@L=350, =382, @C is=52-15A,determine Ze and,and draw the phasor diagram S 1 jaL3 Fig.E6-8a Fig.E6-8 b Solution: Z=R+joL=5+j350:Z3=及+ 0c=2-j38n 43-5+i352-j38=176.74808n Ze-Zi+Za 5+i35+2-i38 t iviao=Z2人=5+j385-15=2498<-7879A: 2-j38 么=Z26=5+5×54-15=2320026A 5+j35 So the phasor diagram is shown as Fig.E6-8 b

电路学习指导 第三章 电阻电路的一般分析 28 4 53.13 A 25 53.13 100 0 eq = ∠ ° ∠ ∠ = = � � ̇ ̇ Z U I U̇R = RI ̇ = 60∠ − 53.13°V U̇ L = jωLI ̇ = 240∠36.87°V 160 143.13 V j 1 = I = ∠ − ° C UC ̇ ̇ ω So the phasor diagram is Fig.E6-7 b The sinusoid is i = 4 2 cos(5000t − 53.13°)A E6-8In circuit shown as Fig.E6-8 a, R1 = 5Ω ， R2 = 2Ω ,ωL = 35Ω , = 38Ω 1 ωC ， I ̇S = 5∠ −15°A ，determine Zeq and 1I ̇ 、 2 I ̇ ，and draw the phasor diagram Fig.E6-8a Fig.E6-8 b Solution: Z1 = R1 + jωL = 5 + j35Ω ； = + = 2 − j38Ω j 1 2 2 C Z R ω = ∠ °Ω + + + = + = 176.7 18.08 5 j35 2 - j38 (5 j35)(2- j38) 1 2 1 2 eq Z Z Z Z Z Current division 5 15 24.98 78.79 A 5 j35 2 - j38 2 - j38 S 1 2 2 1 × ∠ − ° = ∠ − ° + + = + = I Z Z Z I ̇ ̇ ； 5 15 23.20 90.26 A 5 j35 2 - j38 5 j35 S 1 2 1 2 × ∠ − ° = ∠ ° + + + = + = I Z Z Z I ̇ ̇ So the phasor diagram is shown as Fig.E6-8 b

电路学习指导 第三章电阻电路的一般分析 6-10 Problems P6-1M=100W2cos314-120)V,h=502cos(314r+60)V (1)Draw their waves and determinetheir effective values,initial phases, frequencies and periods. (2)Write the corresponding phasors,draw phasor diagram and determine their phase defference. P6-2 Turn these complex numbers into the rectangular form. (1)5∠60°；(2)45∠120°：(3)3.2∠-178°，（④）28∠-295 P6-3 Turn these complex numbers into the exponential form. (1)3.2+j7.5:(2)0.3-j1.5:(3)-125+j94.3:(4)-6-j8 P6-4M=10W2cos(o1+35)V,h=15V2cos1-45)V Determine(1)M=M+h:(②）u=M-h P6-5么=(30+j40)V,=50∠-30V,=(-15+j8)V,0=100∠45V, f=5OH.Write the sinusoid、h、M;(2)Determine =☑+，0。=2+U；(3)Draw phasor diagram,. P6-6☑=50∠30V，☑=100∠-45V，f=100Hz.(1)Write the phase differences between、h、and ua:(②)determine=h+hand =(3)Draw phasor diagram. P6-7i=5cos(3141-120)A,5=10cos(3141+60)A,5=4c0s(314/+60)A (1)Draw the wave of:(2)Write the phasor and draw the phasor diagram. P6-8 U=(100-j50)V,its period is T=10s,Write the instantaneous form. P6-9 The circuit is shown as Fig.P6-9,/=5v/2cos(314/+20)AA,L=10mH, R=50,determine i m and u. ++ u Fig.P6-9 P6-10 In Fig.P6-10a 30V,V2:60V:In Fig.6-10b Vi:20V,V2 80V, V:100V,determine the reading of V. 29

电路学习指导 第三章 电阻电路的一般分析 29 6-10 Problems P6-1 u1 =100 2 cos(314t −120°)V , u2 = 50 2 cos(314t + 60°)V (1) Draw their waves and determinetheir effective values, initial phases, frequencies and periods. (2)Write the corresponding phasors , draw phasor diagram and determine their phase defference. P6-2 Turn these complex numbers into the rectangular form. (1) 5∠60° ； (2) 45∠120° ； (3) 3.2∠ −178°； (4) 28∠ − 295° P6-3 Turn these complex numbers into the exponential form. (1) 3.2 + j7.5 ； (2) 0.3 − j1.5； (3) −125 + j94.3 ； (4) − 6 − j8 P6-4 u1 =10 2 cos(ωt + 35°)V , u2 =15 2 cos(ωt − 45°)V Determine (1) u = u1 + u2 ； (2) u = u1 − u2 P6-5 U̇ 1 = (30 + j40)V ,U̇ 2 = 50∠ − 30°V ,U̇ 3 = (−15 + j8)V,U̇ 4 =100∠45°V , f = 50HZ .Write the sinusoid u1 、 u2 、 u3 、 u4 ； (2)Determine U5 U1 U3 ̇ ̇ ̇ = + ,U6 U2 U4 ̇ = ̇ + ̇ ；(3)Draw phasor diagram. P6-6 U̇ 1 = 50∠30°V , U̇ 2 =100∠ − 45°V , f =100HZ .(1)Write the phase differences between u1 、 u2 、 u1 and u2 ；(2)determine u3 = u1 + u2 and u4 = u1 − u2 ；(3) Draw phasor diagram. P6-7 i1 = 5cos(314t −120°)A ，i2 =10cos(314t + 60°)A ，i3 = 4cos(314t + 60°)A (1)Draw the wave of i1；(2)Write the phasor and draw the phasor diagram. P6-8 U̇ = (100 − j50)V ，its period is 10 s −3 T = ，Write the instantaneous form. P6-9 The circuit is shown as Fig.P6-9 , i = 5 2 cos(314t + 20°)A A， L =10mH ， R = 5Ω ,determine uR 、uL and u . Fig.P6-9 P6-10 In Fig.P6-10a V1：30V， V2 ：60V；In Fig.6-10b V1：20V， V2 ：80V， V3：100V, determine the reading of V

电路学习指导 第三章电阻电路的一般分析 西 ↑W2 R R ⑦ 应 i⑦ Fig.P6-10 a Fig.P6-10 b P6-11 A1=5A,A2 =20A,A3=32A (shown as Fig.P6-11),determine the reading ofA 。④ (A2 H④ Fig.P6-11 Fig.P6-12 P6-12 The voltage and the current are given below,what element P can be? ①"=10cos00r+459V ②/w=10sin100jV i=2sin10r+135)A i=2cos(100r)A (3)u=-10cosN 0J"=10cos314/+45V /=-sin/A i=2cos(314)A P6-13 The circuit is shown as Fig.6-13,=/=10A.Determine and is. Fig.P6-13 F1g.P6-14 P6-14 The circuit is shown as Fig.6-14,/s=220A,Determine and U,And draw the phasor diagram. P6-15 The circuit is shown as Fig.6-15,=/=/3=2A,Determine/and P6-16 Wrte the U or Y of the circuit shown as Fig.P6-15(@is known).And draw the phasor diagram. 30

电路学习指导 第三章 电阻电路的一般分析 30 Fig.P6-10 a Fig.P6-10 b P6-11 A1 = 5A , A2 = 20A , A3 = 32A (shown as Fig.P6-11), determine the reading of A . Fig.P6-11 Fig.P6-12 P6-12 The voltage and the current are given below , what element P can be? (1) ⎩ ⎨ ⎧ = + ° = + ° 2sin(10 135 )A 10cos(10 45 )V i t u t (2) ⎩ ⎨ ⎧ = = 2cos(100 )A 10sin(100 )V i t u t (3) ⎩ ⎨ ⎧ = − = − sin A 10cos V i t u t (4) ⎩ ⎨ ⎧ = = + ° 2cos(314 )A 10cos(314 45 )V i t u t P6-13 The circuit is shown as Fig.6-13， I1 = I 2 =10A . Determine I ̇ and US ̇ . Fig.P6-13 Fig.P6-14 P6-14 The circuit is shown as Fig.6-14， I ̇S = 2∠0°A , Determine I ̇ and U̇ ，And draw the phasor diagram. P6-15 The circuit is shown as Fig.6-15， I1 = I 2 = I 3 = 2A，Determine I ̇ and P6-16 Wrte the U or Y of the circuit shown as Fig.P6-15 (ω is known) .And draw the phasor diagram