
电路学习指导 第七章相量法 第七章相量法 一.基本要求 1.了解正弦量及其三要素,掌握幅值和有效值、频率和周期、相位和相位差的关系,会画 正弦量的波形图。 2.熟练掌握复数代数形式和指数形式之间的相互转换。 3.熟练掌握正弦量与相量之间的变换关系,会画相量图。 4.掌握感抗、容抗的概念。 5.熟悉基尔霍夫定律、欧姆定律的相量形式。 二.本章要点 1.正弦电流i=I cos(ao1+g,),正弦电压u=U cos(o+业):正弦量的三要素是振幅、角 频率和初相。三要素可以确定一个正弦量,也是正弦量之间进行比较和区分的依据。 2正弦量的有效值与报幅的关系为:1一方,人=51:U=方,U.=0 正弦量的周期T),颜率()与角频()的关系为:了=行。=2对- 3.复数的表示形式有代数形式,三角形式和指数形式三种,电工中常用代数形式和指数形 式,要熟练掌握这两种形式间的转换。 4.相量法即是用复数表示正弦量,从而使同频率正弦量的运算简化。振幅相量的模是正弦 量的幅值,它的幅角是正弦量的初相(m=1m∠华),有效值相量(简称相量)的模是正 弦量的有效值,它的幅角是正弦量的初相(1=1上华)。相量和正弦量之间是对应关系, 而不是相等。 5.相量图是在复平面上用有向线段表示相量,相量图形象直观,对正弦交流电路的分析求 解很有帮助。 6.电阻、电感、电容元件伏安关系的相量形式及电阻、电抗 元件 伏安关系 电阻、电抗 相量图 。1 UR=Ri -1-t UL=jX.i XL=@L h-i =joLi 1 Uc=-jXel -i Uc- Xe=C =-joci 56
电路学习指导 第七章 相量法 56 第七章 相量法 一. 基本要求 1.了解正弦量及其三要素,掌握幅值和有效值、频率和周期、相位和相位差的关系,会画 正弦量的波形图。 2.熟练掌握复数代数形式和指数形式之间的相互转换。 3.熟练掌握正弦量与相量之间的变换关系,会画相量图。 4.掌握感抗、容抗的概念。 5.熟悉基尔霍夫定律、欧姆定律的相量形式。 二.本章要点 1.正弦电流 i = Im cos(t +Ψi) ,正弦电压 u =Um cos(t +Ψu ) ;正弦量的三要素是振幅、角 频率和初相。三要素可以确定一个正弦量,也是正弦量之间进行比较和区分的依据。 2.正弦量的有效值与振幅的关系为: I Im 2 1 = , Im = 2I ; U Um 2 1 = , Um = 2U 。 正弦量的周期( T ),频率( f )与角频率( )的关系为: T f 1 = , T f 2π = 2 = 。 3.复数的表示形式有代数形式,三角形式和指数形式三种,电工中常用代数形式和指数形 式,要熟练掌握这两种形式间的转换。 4.相量法即是用复数表示正弦量,从而使同频率正弦量的运算简化。振幅相量的模是正弦 量的幅值,它的幅角是正弦量的初相( Im = ImΨi ),有效值相量(简称相量)的模是正 弦量的有效值,它的幅角是正弦量的初相( I = IΨi )。相量和正弦量之间是对应关系, 而不是相等。 5.相量图是在复平面上用有向线段表示相量,相量图形象直观,对正弦交流电路的分析求 解很有帮助。 6.电阻、电感、电容元件伏安关系的相量形式及电阻、电抗 元件 伏安关系 电阻、电抗 相量图

电路学习指导 第七章相量法 7.基尔霍夫定律的相量形式KCL:对任一节点有Σi=0:KL:对任一回路有ΣU=0。 三.典型例题 例7-1已知:u=10cos(3141+60)V,i=5cos(3141-60)A。要求:1)画出,i的 波形图:2)写出相量心,并画出相量图:3)求,1的相位差Φ。 解:1)画,i波形图。 u,i(V,A) v83605g720t -10+ 图7-14,i波形图 图7-20,1相量图 90-号∠v-7mzwv ∠-60A=354∠-60A i=s 3)u,i的相位差中 中=平.-g=60°-(60)=120 例7-2己知:1=10W2c0s(3141+60)A,2=20V2cos(3141-150)A。求i=1+2。 解:用相量法求解。 i1=10∠60°A,i2=20∠-150°A i=i1+j2=10∠60°A+20∠-150°A =(5+j8.66)A+(-17.32-j10)A =(-12.32-j1.34A =12.39∠-173.8A ∴i1=12.39√2cos3141-173.8)A 例7-3图示电路,电流表A1读数为5A,A2读数为20A,A读数为25A。求电流 表A及A:的读数。 解:这是R、L、C并联电路,设0=U∠0V为参考相量。 由R、L、C中电压、电流相位关系,可以很方便地确定并联支路电流的初相。 i1=5∠0°A,i2=-20A=20∠90A,i3=j25A=25∠90°A 57
电路学习指导 第七章 相量法 57 7.基尔霍夫定律的相量形式 KCL :对任一节点有 I = 0 ; KVL :对任一回路有 U = 0 。 三.典型例题 例 7-1 已知: u =10cos(314t + 60)V , i = 5cos(314t − 60)A。要求:1)画出 u ,i 的 波形图;2)写出相量 U , I ,并画出相量图;3)求 u ,i 的相位差 Φ。 解:1)画 u , i 波形图。 图 7-1 u,i 波形图 图 7-2 U I , 相量图 2) 60 V 7.07 60 V 2 10 U = = 60 A 3.54 60 A 2 5 I = − = − 3) u ,i 的相位差 Φ Φ=Ψu −Ψi = 60 − (60) =120 例 7-2 已知: i1 =10 2 cos(314t + 60)A ,i2 = 20 2 cos(314t −150)A 。求 i = i1 + i2 。 解:用相量法求解。 I 1 =1060A , I 2 = 20 −150A I = I 1 + I 2 =1060A + 20 −150A = (5+ j8.66)A + (−17.32 − j10)A = (−12.32 − j1.34)A =12.39 −173.8A ∴ i1 =12.39 2 cos(314t −173.8)A 例 7-3 图示电路,电流表 A1 读数为 5A ,A2 读数为 20A ,A3 读数为 25A 。求电流 表 A 及 A4 的读数。 解:这是 R 、 L、C 并联电路,设 U =U0V 为参考相量。 由 R 、 L、C 中电压、电流相位关系,可以很方便地确定并联支路电流的初相。 I 1 = 50A , I 2 = −j20A = 2090A , I 3 = j25A = 2590A

电路学习指导 第七章相量法 由KCL:i4=i2+i3=-20A+25A=j5A=5∠90°A i=i1+i4=i1+i2+i2=5+j5A=7.07∠45°A .电流表读数:A为7.07A,A为5A 10@ i tie tis A2A3 图7-3例7-3图 图7-4例7-4图 例7-4图示电路电压表读数为V:15V::80V:V:100V。求电压表V的 读数。 解:这是R、L、C串联电路,可设电流=I∠O°A为参考相量。则各元件电压的初 相即可确定。 U1=15∠0V,U2=80∠90V,U1=100∠-90V 由KL:0=U1+U2+03=(15∠0°+80∠90°+100∠-90)V =15-j20V=25∠-53.13V 电压表V的读数为25V。 四.习题 7-1已知:4=1005c0s(6141-120V,4=502cs3141+60V (①)画出它们的波形图,求出它们的有效值、初相、频率f和周期T: (②)写出它们的相量并画出其相量图,求出它们的相位差。 7一2把下列复数化为代数形式 (1)5∠60°;(2)45∠120°:(3)3.2∠-178°:(4)28∠-295° 7-3把下列复数化为指数形式 (1)3.2+j7.5:(2)0.3-j1.5(3)-125+j94.3:(4)-6-j8 7-4己知:=102cos(+35)V,h=152cos(a-45)V 求:(1)=h+:(②)=山- 7-5已知:U1=(30+j40)V,U2=50∠-30V,U3=(-15+j8)V,04=100∠45V, f=50HZ。求:(1)写出对应正弦量山、3、4:(2)U3=U1+03,0=U2+U4: (3)画出对应的相量图。 7-6己知:01=50∠30V,02=100∠-45V,,f=100HZ.求:(1)写出正弦量山、 山、山与山的相位差中:(②)求山=山+山及山4=山-山2:(3)画出对应的相量图。 7-7己知:4=5cos(3141-120)A,i2=10cos(3141+60)A,3=4c0s(3141+60)A 求:(1)画出的波形图:(2)写出对应的相量,并画出它们相量图。 58
电路学习指导 第七章 相量法 58 由 KCL : I 4 = I 2 + I 3 = −j20A + j25A = j5A = 590A I = I 1 + I 4 = I 1 + I 2 + I 2 = 5+ j5A = 7.0745A ∴电流表读数: A 为 7.07 A, A4 为 5A 图 7-3 例 7-3 图 图 7-4 例 7-4 图 例 7-4 图示电路电压表读数为 V1 :15V ; V2 :80V ; V 3 :100V 。求电压表 V 的 读数。 解:这是 R 、L、C 串联电路,可设电流 I = I0A 为参考相量。则各元件电压的初 相即可确定。 U 1 =150V,U 2 = 8090V ,U 1 =100 − 90V 由 KVL :U =U 1 +U 2 +U 3 = (150+8090+100−90)V =15 − j20V = 25−53.13V 电压表 V 的读数为 25V 。 四.习题 7-1 已知: u1 =100 2 cos(314t −120)V, u2 = 50 2 cos(314t + 60)V (1) 画出它们的波形图,求出它们的有效值、初相、频率 f 和周期 T ; (2) 写出它们的相量并画出其相量图,求出它们的相位差。 7-2 把下列复数化为代数形式 (1) 560 ; (2) 45120 ; (3) 3.2 −178 ; (4) 28 − 295 7-3 把下列复数化为指数形式 (1) 3.2 + j7.5 ; (2) 0.3− j1.5 ; (3) −125 + j94.3 ; (4) − 6 − j8 7-4 已知: u1 =10 2 cos(t + 35)V , u2 =15 2 cos(t − 45)V 求:(1) u = u1 + u2 ; (2) u = u1 −u2 7-5 已知: U 1 = (30 + j40)V ,U 2 = 50 − 30V ,U 3 = (−15 + j8)V ,U 4 =10045V , f = 50HZ 。求:(1)写出对应正弦量 u1、u2 、u3 、u4 ;(2) U5 U1 U3 = + ,U6 U2 U4 = + ; (3)画出对应的相量图。 7-6 已知: U 1 = 5030V , U 2 =100 − 45V , f =100HZ 。求:(1)写出正弦量 u1 、 u2 、 u1 与 u2 的相位差 Φ ;(2)求 u3 = u1 + u2 及 u4 = u1 − u2 ;(3)画出对应的相量图。 7-7 已知: i1 = 5cos(314t −120)A ,i2 =10cos(314t + 60)A ,i3 = 4cos(314t + 60)A 求:(1)画出 1i 的波形图;(2)写出对应的相量,并画出它们相量图

电路学习指导 第七章相量法 7-8己知正弦电压的相量0=(100-j50)V,其周期T=10-3S,写出其瞬时表达式 7-9图示电路中i=5√cos(314t+20)AA,L=10mH,R=5Q。求g、4和u。 + u 题7-9图 7-10(a)图电路中V:30V,V2:60V:(⑥)附图电路中V:20V,V2:80V,V 1O0V。分别求这两个电路中电压表V的读数。 0 (V2 0 (a) (6) 题7-10图 7-11图示电路中A=5A,A2=20A,A3=32A。求电流表A的读数。 C u ④ 。 题7-11图 题7-12图 7-12附图中的电压、电流分别为下述4种情况时,P可能是什么元件。 )=10cos0r+459V ②)=10sn(10V 1i=2sin101+135o)A i=2cos(100t)A (3)u=-10cosrv li=-sintA 4④=10cos(3141+45V i=2cos(3141)A 59
电路学习指导 第七章 相量法 59 7-8 已知正弦电压的相量 U = (100 − j50)V ,其周期 10 S −3 T = ,写出其瞬时表达式。 7-9 图示电路中 i = 5 2 cos(314t + 20)A A, L =10mH ,R = 5 。求 uR 、uL 和 u 。 题 7-9 图 7-10 (a)图电路中 V1 :30V ,V2 :60V ;(b)附图电路中 V1 :20V ,V2 :80V , V3: 100 V 。分别求这两个电路中电压表 V 的读数。 (a) (b) 题 7-10 图 7-11 图示电路中 A1 = 5A, A2 = 20A , A3 = 32A 。求电流表 A 的读数。 题 7-11 图 题 7-12 图 7-12 附图中的电压、电流分别为下述 4 种情况时, P 可能是什么元件。 (1) = + = + 2sin(10 135 )A 10 cos(10 45 )V i t u t (2) = = 2cos(100 )A 10sin(100 )V i t u t (3) = − = − sin A 10cos V i t u t (4) = = + 2cos(314 )A 10cos(314 45 )V i t u t
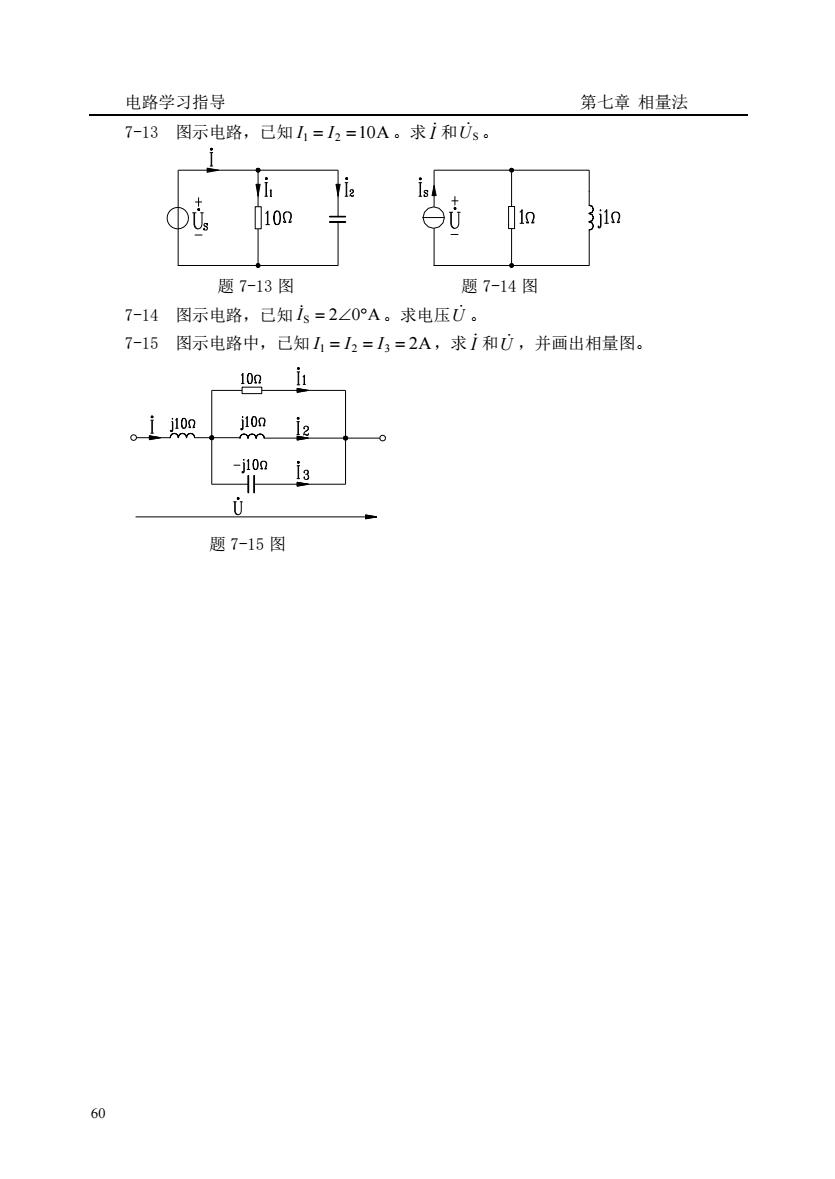
电路学习指导 第七章相量法 7-13图示电路,已知1=12=10A。求i和s。 010n 01n 3jlo 题7-13图 题7-14图 7-14图示电路,已知s=2∠0°A。求电压U。 7-15图示电路中,已知11=12=13=2A,求j和U,并画出相量图。 o140n j100 日 -j10n 0 题7-15图 60
电路学习指导 第七章 相量法 60 7-13 图示电路,已知 I1 = I2 =10A 。求 I 和 US 。 题 7-13 图 题 7-14 图 7-14 图示电路,已知 I S = 20A 。求电压 U 。 7-15 图示电路中,已知 I1 = I2 = I3 = 2A ,求 I 和 U ,并画出相量图。 题 7-15 图