
电路学习指导 第三章电阻电路的一般分析 第三章电阻电路的一般分析 一、基本要求 1、学生通过学习本章会熟练运用结点电压法求解电路,包括含有理想电压源,受控源的 电路。 2、会运用支路电流法、网孔电流法、回路电流法求解电路,包括含有理想电流源,受控 源的电路。 二、本章要点 本章主要介绍求解电路的一般分析方法,这种方法不要求改变电路结构。首先选择一组 合适的电路变量(电流或电压),根据KCL和KVL及元件的电压、电流关系(VCR)建 立该组变量的独立方程组,然后从方程组中解出电路变量。 1、支路电流法: 是以支路电路作为未知量的求解方法。分析电路时,对于n个结点,b条支路的电路 根据KCL,列出(m-1)个结点电流方程,同时根据KVL列出m-b-m-)个独立回路电压 方程,于是,总共得到以支路电流为未知量(即变量)的b独立方程。 必须指出:如果电路的某一个支路含有恒流源,则此支路电流即为该恒流源的电流, 在列含有恒流源回路的电压方程时,可设恒流源的端电压U为未知量。 2、网孔电流法: 是以“假想网孔电流”作为独立变量求解电路的方法,称为网孔电流法。它仅使用 于平面电路。对具有m个网孔的平面电路,网孔电路的一般形式有: (3-1) Rmim+Rm2im2+Rmimt.+Rmmimm=Usmm 3.回路电流法 是以“假想回路电流”作为独立变量的求解电路的方法称为回路电流法。 网孔电流法仅适用于平面电路回路电流法,则无此限制,它适用于平面或非平面电。 对于b条支路,n个结点的电路,回路数(1=b-n+1)与网孔电流法方程(3-1)相似,可 以写出回路电流方程的一般形式,有 Rin+Ri+R+R=Usn (3-2) R21n+R222+R23++R2=U522 Rnin+Rpip+Ri+.+R=Us 21
电路学习指导 第三章 电阻电路的一般分析 21 第三章 电阻电路的一般分析 一、基本要求 1、学生通过学习本章会熟练运用结点电压法求解电路,包括含有理想电压源,受控源的 电路。 2、会运用支路电流法、网孔电流法、回路电流法求解电路,包括含有理想电流源,受控 源的电路。 二、本章要点 本章主要介绍求解电路的一般分析方法,这种方法不要求改变电路结构。首先选择一组 合适的电路变量(电流或电压),根据 KCL 和 KVL 及元件的电压、电流关系(VCR)建 立该组变量的独立方程组,然后从方程组中解出电路变量。 1、支路电流法: 是以支路电路作为未知量的求解方法。分析电路时,对于 n 个结点,b 条支路的电路 根据 KCL,列出(n-1)个结点电流方程,同时根据 KVL 列出 m=b-(n-1)个独立回路电压 方程,于是,总共得到以支路电流为未知量(即变量)的 b 独立方程。 必须指出:如果电路的某一个支路含有恒流源,则此支路电流即为该恒流源的电流, 在列含有恒流源回路的电压方程时,可设恒流源的端电压 U 为未知量。 2、网孔电流法: 是以“假想网孔电流”作为独立变量求解电路的方法,称为网孔电流法。它仅使用 于平面电路。对具有 m 个网孔的平面电路,网孔电路的一般形式有: R11im1+R12im2+R13im3+.+R1mimm=uS11 R21im1+R22im2+R23im3+.+R2mimm=uS22 . Rm1im1+Rm2im2+Rm3im3+.+Rmmimm=uSmm 3. 回路电流法 是以“假想回路电流”作为独立变量的求解电路的方法称为回路电流法。 网孔电流法仅适用于平面电路,回路电流法, 则无此限制,它适用于平面或非平面电。 对于 b 条支路,n 个结点的电路,回路数(l=b-n+1)与网孔电流法方程(3-1)相似,可 以写出回路电流方程的一般形式,有 R11il1+R12il2+R13il3+.+R1lill=uS11 R21il1+R22il2+R23il3+.+R2lill=uS22 . Rl1il1+Rl2iL2+Rl3il3+.+Rllill=uSll (3-1) (3-2)

电路学习指导 第三章电阻电路的一般分析 (1)式(3-1)和(3-2)中有相同下标的电阻R1.R2R:等是各网孔和各回路的自阻,有不 同下标的电阻R2.R:R,等是各网孔和回路的互阻。 (2)自阻总是正的,互阻取正还是取负,则由相关的两个网孔电流和回路电流通过公共电阻 时两者的参考方向是否相同来决定,相同时取正,相反时取负。显然,若两个回路和网孔间 没有公共电阻,则相应的互阻为零 (3)方程右方的UsU22分别为网孔和回路1,2等中电压源的代数和,取和时,各电 压源的方向与网孔和回路电流的方向一致的电压源前应取“一”号,否则取“+”号。 4.结点电压法 结点电压法是以结点电压为未知量,应用KCL列出结点电流方程,然后用结点电压 来表示各支路电流代入结点电流方程。一个具有(+1)个结点,b条支路的电路当选定 任一结点为参考结点后,其余的n个结点是独立的,它的结点电压方程有: (3-3) 式(3-3)中具有相同下标的电导G.Gm.G33等是各结点的自电导,具有不同下标的电导 G2.G:等是各结点间的互电导而自导总是正的,互导总是负的。显然,如果两个结点之 间没有电导的支路而直接相连,则相应的互导为零。此外,在分析电路中遇到的特殊情 况,将通过实例给予分析和说明。 5.特殊问愿 在支路电流法,网孔电流法,回路电流法和结点电压法中遇到受空源时如何处理? (1)当电路中含有受控源时,先将受控电源视为独立电源列写方程,再将受控源的控制量 用支路电流、网孔电流、回路电流、结点电压来表示后带入方程加以整理.其余情况将通 过实列给予加以分析。 三、典型例题 例3一1如图3一1所示电路,试用支路电流法求各支路电流,2,。 解:(1)选定各支路电流的参考方向如图所示。 112 (2)结点数2、独立结点数: n-1=2-1=1个, 故只能列一个kCL方程: -I1+H2+H3=0 ① (3)独立回路数 b-(n-1)=3-1=2: 以支路电流为变量按顺时针绕行方向列出网孔 回路的KVL方程: 图3一1例3-1图 22
电路学习指导 第三章 电阻电路的一般分析 22 (1)式(3-1)和(3-2)中有相同下标的电阻 R11,R22,R33 等是各网孔和各回路的自阻,有不 同下标的电阻 R12,R23,R31 等是各网孔和回路的互阻。 (2)自阻总是正的,互阻取正还是取负,则由相关的两个网孔电流和回路电流通过公共电阻 时两者的参考方向是否相同来决定,相同时取正,相反时取负。显然,若两个回路和网孔间 没有公共电阻,则相应的互阻为零. (3)方程右方的 uS11,uS22,.分别为网孔和回路 1,2.等中电压源的代数和,取和时,各电 压源的方向与网孔和回路电流的方向一致的电压源前应取“—”号,否则取“+”号。 4.结点电压法 结点电压法是以结点电压为未知量,应用 KCL 列出结点电流方程,然后用结点电压 来表示各支路电流代入结点电流方程。一个具有(n+1)个结点,b 条支路的电路当选定 任一结点为参考结点后,其余的 n 个结点是独立的,它的结点电压方程有: G11un1+ G12un1+ G13un3+ . + G1nunn=iS11 G21un1+ G22un2+ G23un3+ . + G2nunn=iS11 . Gn1un1+ Gn2un2+ Gn3un3+ . + Gnnunn=iSnn 式(3-3)中具有相同下标的电导 G11,G22,G33 等是各结点的自电导,具有不同下标的电导 G12,G13.等是各结点间的互电导而自导总是正的,互导总是负的。显.然,如果两个结点之 间没有电导的支路而直接相连,则相应的互导为零。此外,在分析电路中遇到的特殊情 况,将通过实例给予分析和说明。 5.特殊问题 在支路电流法,网孔电流法,回路电流法和结点电压法中遇到受空源时如何处理? (1)当电路中含有受控源时,先将受控电源视为独立电源列写方程,再将受控源的控制量 用支路电流、网孔电流、回路电流、结点电压来表示后带入方程加以整理.其余情况将通 过实列给予加以分析。 三、 典型例题 例 3-1 如图 3—1 所示电路,试用支路电流法求各支路电流 I1,I2,I3 。 解:(1)选定各支路电流的参考方向如图所示。 (2)结点数 2、独立结点数: n-1=2-1=1 个, 故只能列一个 KCL 方程: -I1+I2+I3=0 ① (3)独立回路数: l=b-(n-1)=3-1=2; 以支路电流为变量按顺时针绕行方向列出网孔 回路的 KVL 方程: 图 3—1 例 3-1 图 (3-3)
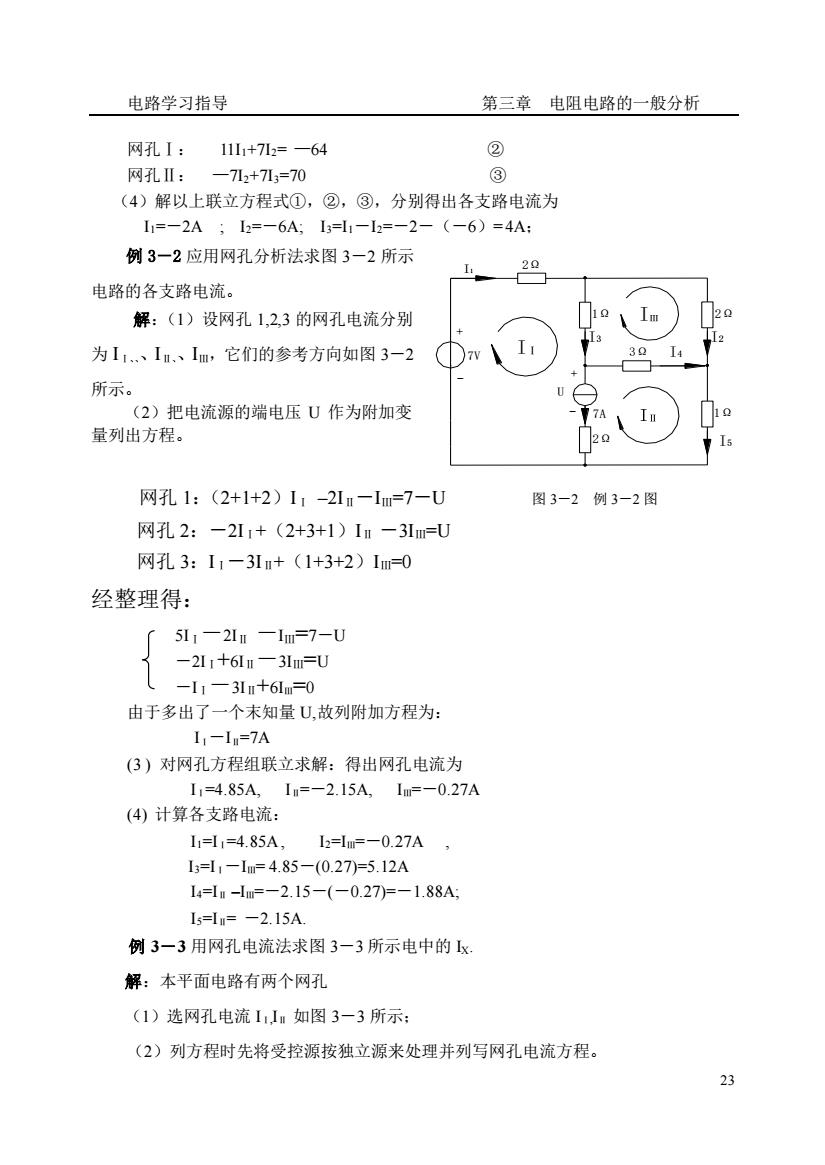
电路学习指导 第三章电阻电路的一般分析 网孔I: 11l1+72=-64 ② 网孔Ⅱ:-712+713=70 (4)解以上联立方程式①,②,③,分别得出各支路电流为 I1=-2A;I2=-6A;I=l1-I2=-2-(-6)=4A: 例3一2应用网孔分析法求图3一2所示 20 电路的各支路电流。 解:(1)设网孔1,2,3的网孔电流分别 为11、I.、Im,它们的参考方向如图3一2 所示。 (2)把电流源的端电压U作为附加变 量列出方程。 网孔1:(2+1+2)11-21m-1m=7-U 图3-2例3-2图 网孔2:-211+(2+3+1)1m-31m=U 网孔3:11-31m+(1+3+2)1m=0 经整理得: 「5L1-21n-lm=7-U -2I1+6ln一3m=U -1-3+61-0 由于多出了一个末知量U,故列附加方程为: 1,-1a=7A (3)对网孔方程组联立求解:得出网孔电流为 11=4.85A,In=-2.15A,1m=-0.27A (④计算各支路电流: 11=L,=485A 12=l=-0.27A I=l1-1m=4.85-(0.27)=5.12A 14=lm-1m=-2.15-(-0.27)=-1.88A I5=m=-2.15A 例3一3用网孔电流法求图3一3所示电中的x 解:本平面电路有两个网孔 (1)选网孔电流1m如图3一3所示: (2)列方程时先将受控源按独立源来处理并列写网孔电流方程。 23
电路学习指导 第三章 电阻电路的一般分析 23 网孔Ⅰ: 11I1+7I2= —64 ② 网孔Ⅱ: —7I2+7I3=70 ③ (4)解以上联立方程式①,②,③,分别得出各支路电流为 I1=-2A ; I2=-6A; I3=I1-I2=-2-(-6)= 4A; 例 3-2 应用网孔分析法求图 3-2 所示 电路的各支路电流。 解:(1)设网孔 1,2,3 的网孔电流分别 为 IⅠ、IⅡ、IⅢ,它们的参考方向如图 3-2 所示。 (2)把电流源的端电压 U 作为附加变 量列出方程。 网孔 1:(2+1+2)IⅠ –2IⅡ-IⅢ=7-U 图 3-2 例 3-2 图 网孔 2:-2IⅠ+(2+3+1)IⅡ -3IⅢ=U 网孔 3:IⅠ-3IⅡ+(1+3+2)IⅢ=0 经整理得: 5IⅠ-2IⅡ -IⅢ=7-U -2IⅠ+6IⅡ-3IⅢ=U -IⅠ-3IⅡ+6IⅢ=0 由于多出了一个末知量 U,故列附加方程为: IⅠ-IⅡ=7A (3 ) 对网孔方程组联立求解:得出网孔电流为 IⅠ=4.85A, IⅡ=-2.15A, IⅢ=-0.27A (4) 计算各支路电流: I1=IⅠ=4.85A, I2=IⅢ=-0.27A , I3=IⅠ-IⅢ= 4.85-(0.27)=5.12A I4=IⅡ –IⅢ=-2.15-(-0.27)=-1.88A; I5=IⅡ= -2.15A. 例 3-3 用网孔电流法求图 3-3 所示电中的 IX. 解:本平面电路有两个网孔 (1)选网孔电流 IⅠ,IⅡ 如图 3-3 所示; (2)列方程时先将受控源按独立源来处理并列写网孔电流方程。 + 7A 2Ω - - U I5 1Ω I3 1Ω + IⅠ 7V I1 2Ω 2Ω I2 3Ω I4 IⅢ
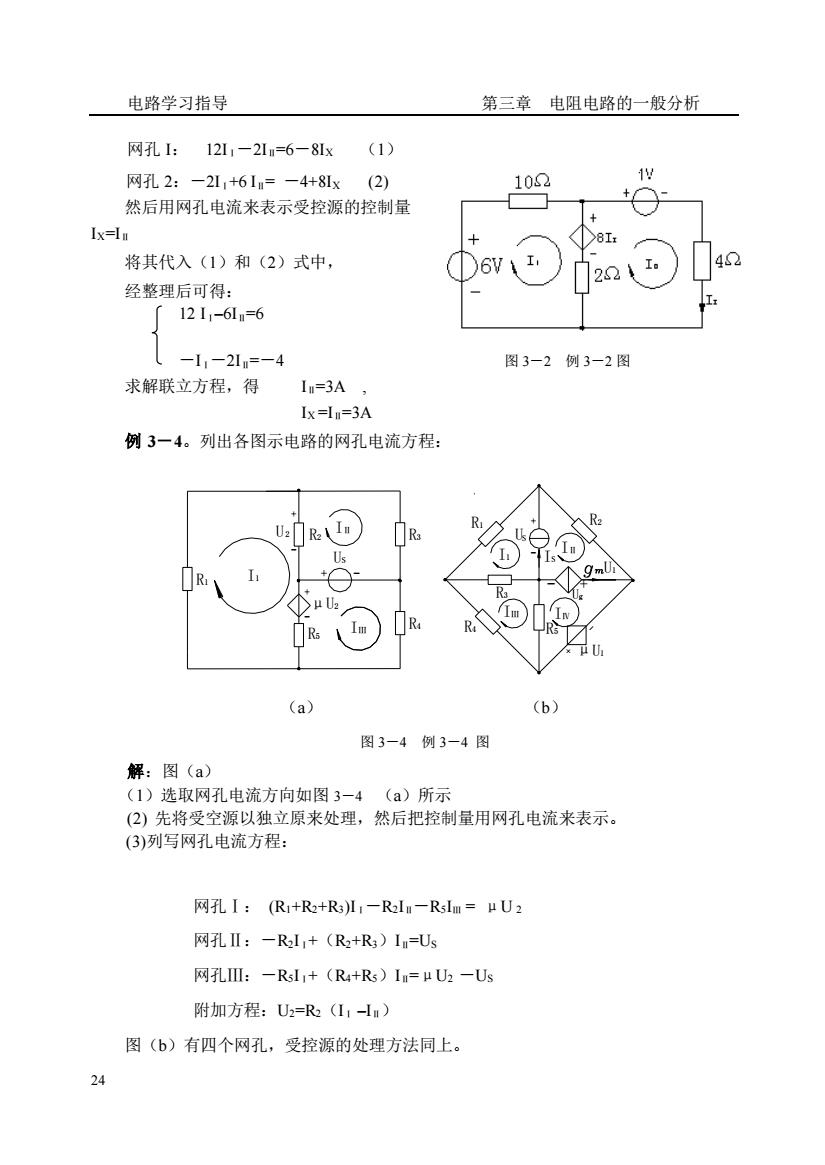
电路学习指导 第三章电阻电路的一般分析 网f孔:121-2I=6-81x(1) 网孔2:-21,+61=-4+8x(2) 102 然后用网孔电流来表示受控源的控制量 Ix=I >81 将其代入(1)和(2)式中 22. 42 经整理后可得: 12I1-6m=6 L-1.-21=-4 图3-2例3-2图 求解联立方程,得 I=3A, Ix=I1=3A 例3一4。列出各图示电路的网孔电流方程: J (b) 图3-4例3-4图 解:图(a) (1)选取网孔电流方向如图3-4(a)所示 (2)先将受空源以独立原来处理,然后把控制量用网孔电流来表示。 (3)列写网孔电流方程: 网孔I:(R+R+R)-Rla-Rsm=uU 网孔Ⅱ:-Rl,+(R+R3)I=Us 网孔I:-Rsl+(R4+Rs)I=μU2-Us 附加方程:U2=R(11-) 图(b)有四个网孔,受控源的处理方法同上。 24
电路学习指导 第三章 电阻电路的一般分析 24 网孔 I: 12IⅠ-2IⅡ=6-8IX (1) 网孔 2:-2IⅠ+6 IⅡ= -4+8IX (2) 然后用网孔电流来表示受控源的控制量 IX=IⅡ 将其代入(1)和(2)式中, 经整理后可得: 12 IⅠ–6IⅡ=6 -IⅠ-2IⅡ=-4 图 3-2 例 3-2 图 求解联立方程,得 IⅡ=3A , IX =IⅡ=3A 例 3-4。列出各图示电路的网孔电流方程: R1 I1 + - μU2 R5 - + IⅢ R4 U2 R2 - + US IⅡ R3 U1 R4 R3 IⅢ R5 + - μU1 Ug IⅣ - + R1 US I1 - + R2 IⅡ IS (a) (b) 图 3-4 例 3-4 图 解:图(a) (1)选取网孔电流方向如图 3-4 (a)所示 (2) 先将受空源以独立原来处理,然后把控制量用网孔电流来表示。 (3)列写网孔电流方程: 网孔Ⅰ: (R1+R2+R3)IⅠ-R2IⅡ-R5IⅢ = μU 2 网孔Ⅱ:-R2IⅠ+(R2+R3)IⅡ=US 网孔Ⅲ:-R5IⅠ+(R4+R5)IⅡ=μU2 -US 附加方程:U2=R2(IⅠ –IⅡ) 图(b)有四个网孔,受控源的处理方法同上
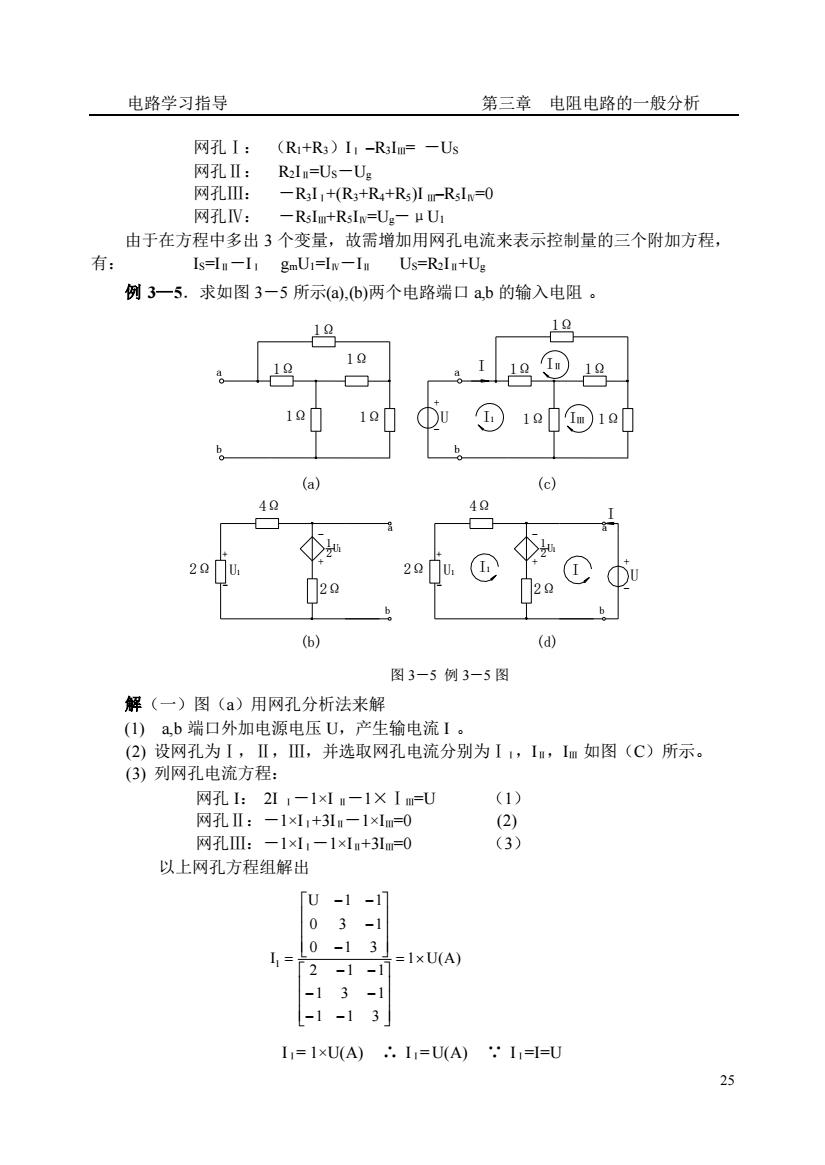
电路学习指导 第三章电阻电路的一般分析 网孔I: (R+R3)I1-R3Im=-Us 网孔: R2I=Us-U: K网孔Π: -R3I:+(R3+R4+Rs)ImrRsIN-0 网V: -Rslr+Rln=Ue-μU1 由于在方程中多出3个变量,故需增加用网孔电流来表示控制量的三个附加方程 有 Is=I-11 gmU1=IN-In Us=R2l+Ug 例3一5.求如图3一5所示(a.b)两个电路端口ab的输入电阻。 19 19 19 19 10h 1 6 40 40 20 2 U. ①u 2 6 (d) 图3-5例3-5图 解(一)图(a)用网孔分析法米解 (1)ab端口外加电源电压U,产生输电流1。 (2)设网孔为I,Ⅱ,并选取网孔电流分别为I,I,【m如图(C)所示。 (3)列网孔电流方程: 网孔1:2I1-1×lm-1×1=U (1) 网孔Ⅱ:-1×11+31m-1×1m=0 2) 网孔:一1×1-1×n+3m=0 (3) 以上网孔方程组解出 「u-1-11 03-1 0-13 2-1 =1×U(A) -13- -1-13 I=1xU(A).1=U(A) 25
电路学习指导 第三章 电阻电路的一般分析 25 网孔Ⅰ: (R1+R3)IⅠ –R3IⅢ= -US 网孔Ⅱ: R2IⅡ=US-Ug 网孔Ⅲ: -R3IⅠ+(R3+R4+R5)I Ⅲ–R5IⅣ=0 网孔Ⅳ: -R5IⅢ+R5IⅣ=Ug-μU1 由于在方程中多出 3 个变量,故需增加用网孔电流来表示控制量的三个附加方程, 有: IS=IⅡ-IⅠ gmU1=IⅣ-IⅡ US=R2IⅡ+Ug 例 3—5.求如图 3-5 所示(a),(b)两个电路端口 a,b 的输入电阻 。 1Ω b a b a U + - I1 IⅡ IⅢ b a + - 2Ω U1 + - 1 2 U1 2Ω 2Ω 2Ω U1 - + + - 4Ω b a U 1 2 1 I1 I I - U + I 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 1Ω 4Ω (a) (c) (b) (d) 图 3-5 例 3-5 图 解(一)图(a)用网孔分析法来解 (1) a,b 端口外加电源电压 U,产生输电流 I 。 (2) 设网孔为Ⅰ,Ⅱ,Ⅲ,并选取网孔电流分别为ⅠⅠ,IⅡ,IⅢ 如图(C)所示。 (3) 列网孔电流方程: 网孔 I: 2I Ⅰ-1×I Ⅱ-1×ⅠⅢ=U (1) 网孔Ⅱ:-1×IⅠ+3IⅡ-1×IⅢ=0 (2) 网孔Ⅲ:-1×IⅠ-1×IⅡ+3IⅢ=0 (3) 以上网孔方程组解出 1 U(A) 1 1 3 1 3 1 2 1 1 0 1 3 0 3 1 U 1 1 I 1 = − − − − − − − − − − = IⅠ= 1×U(A) ∴ IⅠ= U(A) ∵ IⅠ=I=U
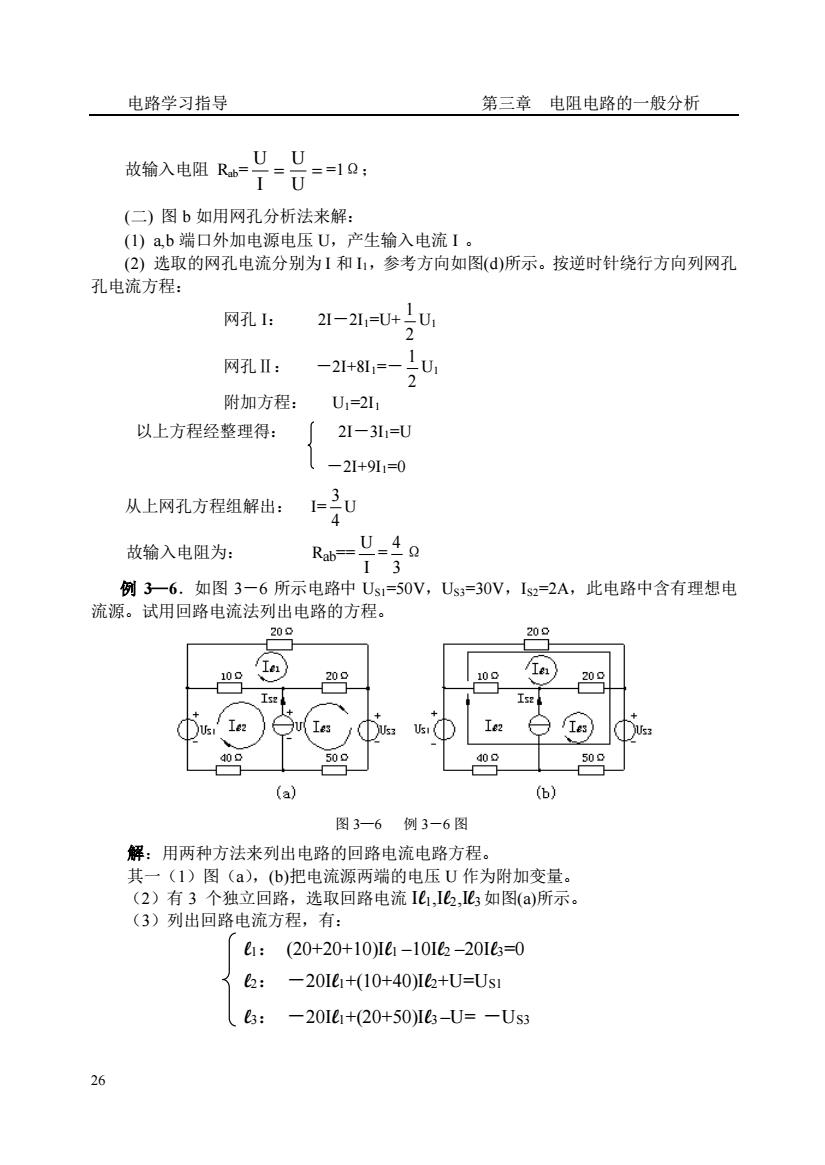
电路学习指导 第三章电阻电路的一般分析 故输入电阻R·=· 7=10: (二)图b如用网孔分析法来解: (1)ab端口外加电源电压U,产生输入电流1。 (2)选取的网孔电流分别为1和,参考方向如图(@d)所示。按逆时针绕行方向列网孔 孔电流方程: 网孔: 21-21=U4U 网孔Ⅱ: -28-一2" 附加方程: U1=2I1 以上方程经整理得: 2I-31=U -21+9I=0 从上网孔方程组解出:0 故输入电阻为: Ra-U-0 例3一6.如图3-6所示电路中Us1=50V,Us3=30V,Is2=2A,此电路中含有理想电 流源。试用回路电流法列出电路的方程。 0 20 109 09 100 209 Ie 白© 409 (a) 6) 图3一6例3-6图 解:用两种方法来列出电路的回路电流电路方程。 其一(1)图(a),(b)把电流源两端的电压U作为附加变量。 (2)有3个独立回路,选取回路电流I,16,心如图(a)所示。 (3)列出回路电流方程,有: L:(20+20+10)IG-10I6-20I6=0 6: -20IC+(10+40)IC2+U=Us1 -20I+20+50)I03-U=-Us3 26
电路学习指导 第三章 电阻电路的一般分析 26 故输入电阻 Rab= = = U U I U =1Ω; (二) 图 b 如用网孔分析法来解: (1) a,b 端口外加电源电压 U,产生输入电流 I 。 (2) 选取的网孔电流分别为 I 和 I1,参考方向如图(d)所示。按逆时针绕行方向列网孔 孔电流方程: 网孔 I: 2I-2I1=U+ 2 1 U1 网孔Ⅱ: -2I+8I1=- 2 1 U1 附加方程: U1=2I1 以上方程经整理得: 2I-3I1=U -2I+9I1=0 从上网孔方程组解出: I= 4 3 U 故输入电阻为: Rab== I U = 3 4 Ω 例 3—6.如图 3-6 所示电路中 US1=50V,US3=30V,IS2=2A,此电路中含有理想电 流源。试用回路电流法列出电路的方程。 图 3—6 例 3-6 图 解:用两种方法来列出电路的回路电流电路方程。 其一(1)图(a),(b)把电流源两端的电压 U 作为附加变量。 (2)有 3 个独立回路,选取回路电流 Il1,Il2,Il3 如图(a)所示。 (3)列出回路电流方程,有: l1: (20+20+10)Il1 –10Il2 –20Il3=0 l2: -20Il1+(10+40)Il2+U=US1 l3: -20Il1+(20+50)Il3 –U= -US3

电路学习指导 第三章电阻电路的一般分析 因多出一个变量,必须列一个附加方程 Is2=IC3-I62=2A: 经整理得: 50I1-10I02-20Ie=0 1016+50I62+U=50 -20IC1+70I03-U=-30 I6-I2=2A 由此可见,如果在含有理想电流源的支路比较多时列方程及解方程都有困难。所以 为了避免这个困难,这道题也可以这样选取独立回路。回路电流方向如图(b)所示。 (二),图b:(1)把理想电流源仅仅属于一个回路来选取独立回路 (2)回路电流参考方向如图所示。(有3个独立回路) (3)列方程: fL1:(20+20+10)1L1+20Il2-20IL=0 了6:20I1+(20+50+40)Il+50IL3=Us1-Usg Len: I03=Is2=2A 经整理得: 5010+2012-20I3-0 2014+11012+50163=20 1L=5=2A 由此可见,此种方法比前一种方法减少了两个变量,解方程也比较方便,所以象这 种情况下还是用这种方法比较合适。 例3一7.应用回路电流法求图3一7所 示的各支路电流。 解:(1)此电路共有3个独立回路。 (2)先将受控电流源以独立源来处 理,然后把控制量用回路电路来表示。 (3)根据电流源只能属于一个回路的 原则选取回路电流IL1I213 (4)列出回路电流方程,有 图3-7例3-7图 C16=5A I6=5U -2101+2162+1+2+21L3=-0 附加方程:U1=211一1 27
电路学习指导 第三章 电阻电路的一般分析 27 因多出一个变量,必须列一个附加方程; IS2=Il3 –Il2=2A; 经整理得: 50Il1-10Il2-20Il3=0 -10Il1+50Il2+U=50 -20Il1+70Il3-U= -30 Il3-Il2=2A 由此可见,如果在含有理想电流源的支路比较多时列方程及解方程都有困难。所以 为了避免这个困难,这道题也可以这样选取独立回路。回路电流方向如图(b)所示。 (二),图(b);(1)把理想电流源仅仅属于一个回路来选取独立回路 。 (2)回路电流参考方向如图所示。(有 3 个独立回路) (3)列方程: l 1: (20+20+10)I l1+20I l 2 –20I l3=0 l2: 20I l1+(20+50|+40)Il2+50I l 3=US1-US3 l 3: I l3=IS2=2A 经整理得: 50 I l1 +20 I l2 -20 I l3 =0 20 I l1 +110 I l2 +50 I l3 =20 I l3=IS=2A 由此可见,此种方法比前一种方法减少了两个变量,解方程也比较方便,所以象这 种情况下还是用这种方法比较合适。 例 3—7.应用回路电流法求图 3-7 所 示的各支路电流。 解:(1)此电路共有 3 个独立回路。 (2)先将受控电流源以独立源来处 理,然后把控制量用回路电路来表示。 (3)根据电流源只能属于一个回路的 原则选取回路电流 I l 1 ,I l2, I l3 (4)列出回路电流方程,有 图 3—7 例 3-7 图 I l1 =5A I l2 =5U1 -2 I l1+2 I l2 +(1+2+2)I l3=0 附加方程:U1=2 (I l1- I l3)
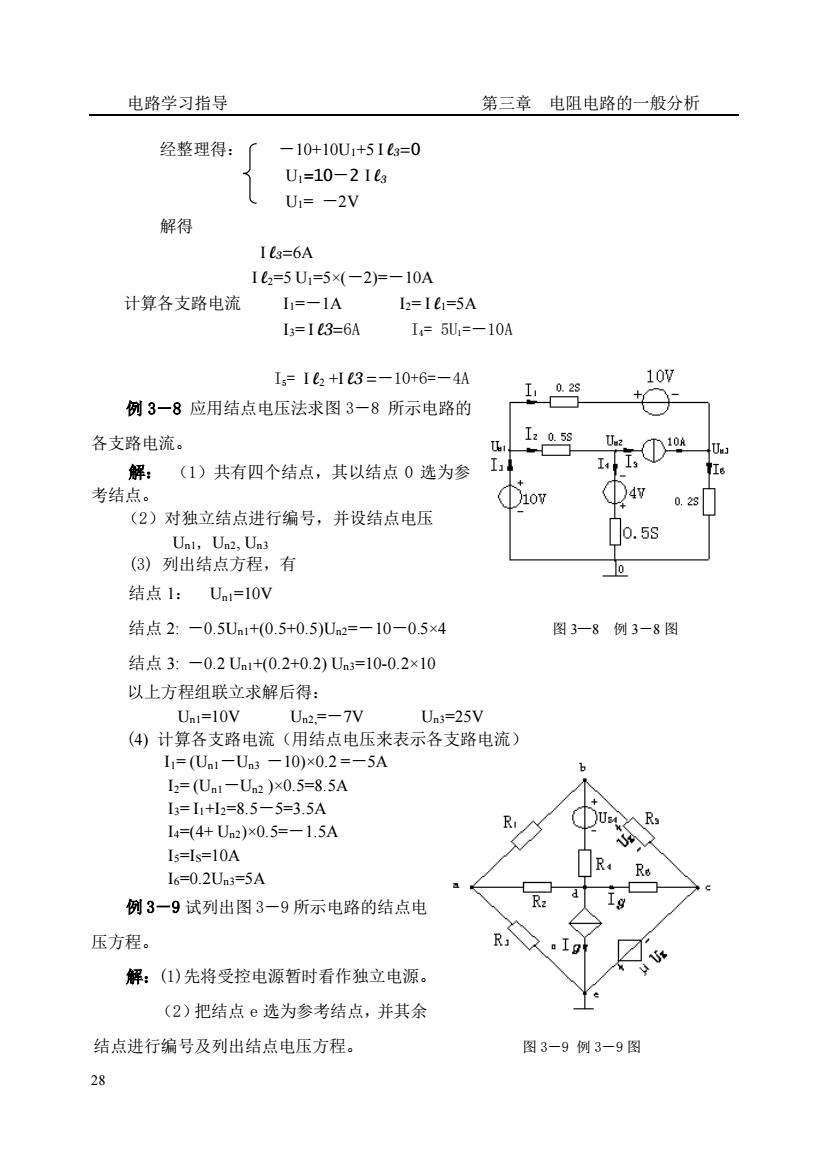
电路学习指导 第三章电阻电路的一般分析 经整理得: -10+10U1+5143=0 U1=10-213 U1=-2V 解得 =6A I82=5U1=5×(-2)=-10A 计算各支路电流 =-1A I2=I=5A I3=I3=6A I=5U=-10A I=I62+H3=-10+6=-4A 10W 102 例3一8应用结点电压法求图3一8所示电路的 各支路电流。 3058 I. ①0 解:(1)共有四个结点,其以结点0选为参 I 11 考结点。 (2)对独立结点进行编号,并设结点电压 Unl,Ua2,Un3 0.5s (③)列出结点方程,有 0 结点1:Un=10V 结点2:-0.5Un1+0.5+0.5U2=-10-05×4 图3一8例3-8图 结点3:-0.2Un1+0.2+0.2)Un=10-0.2×10 以上方程组联立求解后得: U=10V Un2.=-7V U:=25V (4)计算各支路电流(用结点电压来表示各支路电流) 1=(Un1-Un3-10)×0.2=-5A 12=(Ua1-Ua2)×0.5=8.5A =1+l=8.5-5=3.5A L4-(4+U2)×0.5=-1.5A I=I=10A R I6=0.2Un3=5A 例3一9试列出图3一9所示电路的结点电 压方程。 R 解:(1)先将受控电源暂时看作独立电源。 (2)把结点e选为参考结点,并其余 结点进行编号及列出结点电压方程。 图3-9例3-9图 28
电路学习指导 第三章 电阻电路的一般分析 28 经整理得: -10+10U1+5 I l3=0 U1=10-2 I l3 U1= -2V 解得 I l3=6A I l2=5 U1=5×(-2)=-10A 计算各支路电流 I1=-1A I2= I l1=5A I3= I l3=6A I4= 5U1=-10A I5= I l2 +I l3 =-10+6=-4A 例 3-8 应用结点电压法求图 3-8 所示电路的 各支路电流。 解: (1)共有四个结点,其以结点 0 选为参 考结点。 (2)对独立结点进行编号,并设结点电压 Un1, Un2, Un3 (3) 列出结点方程,有 结点 1: Un1=10V 结点 2: -0.5Un1+(0.5+0.5)Un2=-10-0.5×4 图 3—8 例 3-8 图 结点 3: -0.2 Un1+(0.2+0.2) Un3=10-0.2×10 以上方程组联立求解后得: Un1=10V Un2,=-7V Un3=25V (4) 计算各支路电流(用结点电压来表示各支路电流) I1= (Un1-Un3 -10)×0.2 =-5A I2= (Un1-Un2 )×0.5=8.5A I3= I1+I2=8.5-5=3.5A I4=(4+ Un2)×0.5=-1.5A I5=IS=10A I6=0.2Un3=5A 例 3-9 试列出图 3-9 所示电路的结点电 压方程。 解:(1)先将受控电源暂时看作独立电源。 (2)把结点 e 选为参考结点,并其余 结点进行编号及列出结点电压方程。 图 3-9 例 3-9 图
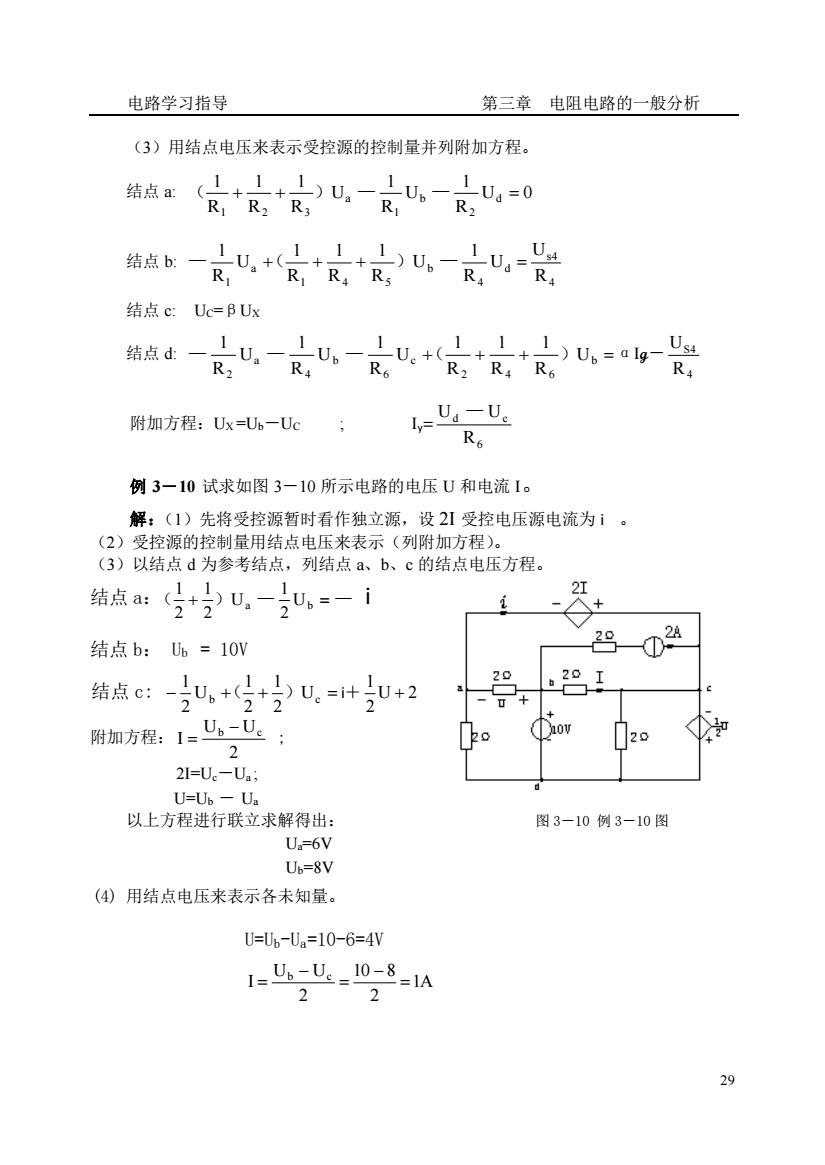
电路学习指导 第三章电阻电路的一般分析 (3)用结点电压来表示受控源的控制量并列附加方程。 结点a 官+官)u,一u-u,=0 1 u+++)u一是 结点b一R 1 结点c:Uc=BUx 结点d: U一R4 R2 U一R6 U.a lg-Ust R 附加方程:Ux=U6一Uc; 1,0g-U R。 例3一10试求如图3一10所示电路的电压U和电流1。 解:(1)先将受控源暂时看作独立源,设2I受控电压源电流为ⅰ。 (2)受控源的控制量用结点电压来表示(列附加方程)。 (3)以结点d为参考结点,列结点a、b、c的结点电压方程。 结点a:(+U,-u=-i 结点b:h=10V 29 结点c:-,+u.=计+2 20 -+ 附加方程:1=,U: ov 20 ① 2=U。-U2 U=U-U. 以上方程进行联立求解得出: 图3-10例3-10图 U=6V Ub=8V (4)用结点电压来表示各未知量。 U=U。-U4=10-6=4V 1=U-u_10-8-1A 29
电路学习指导 第三章 电阻电路的一般分析 29 (3)用结点电压来表示受控源的控制量并列附加方程。 结点 a: U 0 R 1 U R 1 U R 1 R 1 R 1 d 2 b 1 a 1 2 3 ( + + ) — — = 结点 b: 4 s4 d 4 b 1 4 5 a 1 R U U R 1 U R 1 R 1 R 1 U R 1 — +( + + ) — = 结点 c: UC=βUX 结点 d: + + + b = 2 4 6 c 6 b 4 a 2 U R 1 R 1 R 1 U R 1 U R 1 U R 1 — — — ( ) αIg- 4 S4 R U 附加方程:UX =Ub-UC ; Iy= 6 d c R U — U 例 3-10 试求如图 3-10 所示电路的电压 U 和电流 I。 解:(1)先将受控源暂时看作独立源,设 2I 受控电压源电流为 i 。 (2)受控源的控制量用结点电压来表示(列附加方程)。 (3)以结点 d 为参考结点,列结点 a、b、c 的结点电压方程。 结点 a:( + ) a — Ub = — 2 1 U 2 1 2 1 i 结点 b: Ub = 10V 结点 c: − b + + Uc = 2 1 2 1 U 2 1 ( ) i+ U 2 2 1 + 附加方程: 2 U U I b − c = ; 2I=Uc-Ua ; U=Ub - Ua 以上方程进行联立求解得出: 图 3-10 例 3-10 图 Ua=6V Ub=8V (4) 用结点电压来表示各未知量。 U=Ub-Ua=10-6=4V 1A 2 10 8 2 U U I b c = − = − =
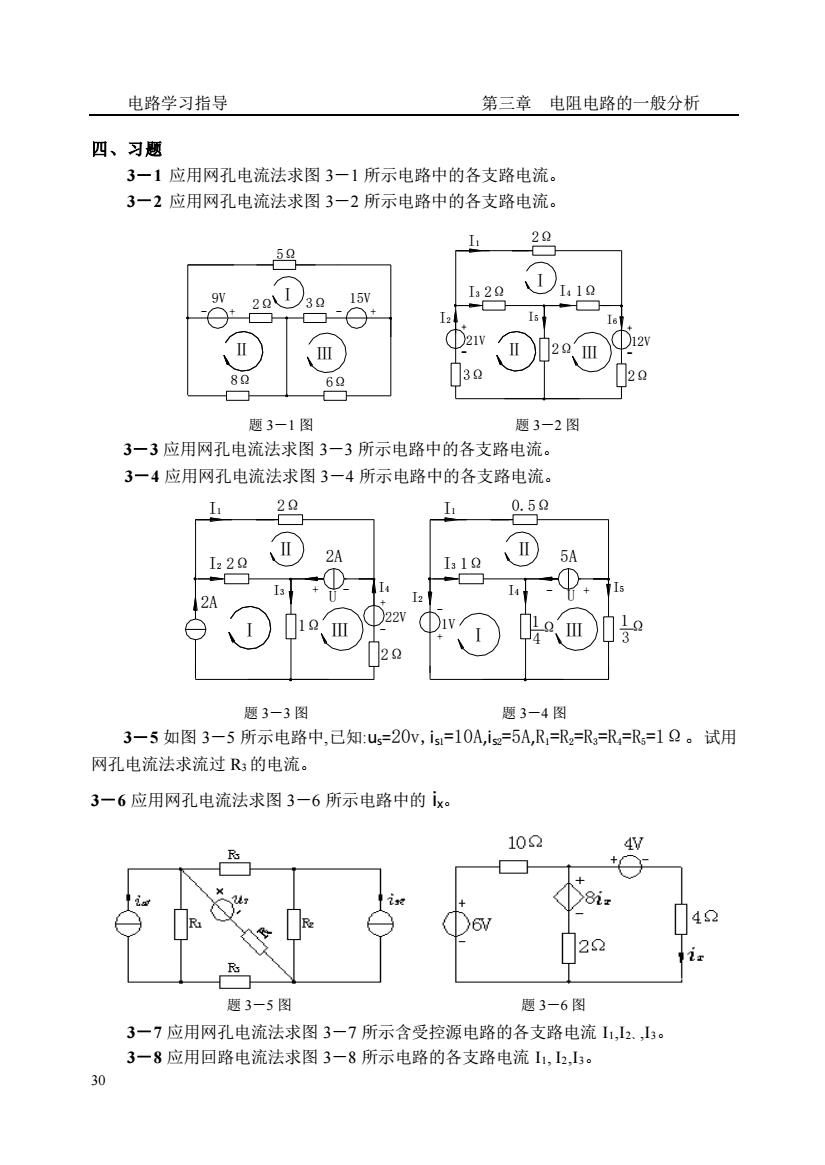
电路学习指导 第三章电阻电路的一般分析 四、习题 3一1应用网孔电流法求图3一1所示电路中的各支路电流 3一2应用网孔电流法求图3一2所示电路中的各支路电流。 5 RO 60 J30 2 题3-1图 题3-2图 3一3应用网孔电流法求图3一3所示电路中的各支路电流。 3一4应用网孔电流法求图3一4所示电路中的各支路电流。 20 0.50 2A 2 题3一3图 题3一4图 3-5如图3-5所示电路中,已知:u=20v,1s=10A,i=5A,R=R,=R=R=R=1Q。试用 网孔电流法求流过R3的电流。 3一6应用网孔电流法求图3一6所示电路中的x。 10 题3-5图 题3-6图 3一7应用网孔电流法求图3一7所示含受控源电路的各支路电流11,2.,山3: 3一8应用回路电流法求图3一8所示电路的各支路电流1,2,5。 30
电路学习指导 第三章 电阻电路的一般分析 30 四、习题 3-1 应用网孔电流法求图 3-1 所示电路中的各支路电流。 3-2 应用网孔电流法求图 3-2 所示电路中的各支路电流。 题 3-1 图 题 3-2 图 3-3 应用网孔电流法求图 3-3 所示电路中的各支路电流。 3-4 应用网孔电流法求图 3-4 所示电路中的各支路电流。 题 3-3 图 题 3-4 图 3-5 如图 3-5 所示电路中,已知:us=20v,is1=10A,is2=5A,R1=R2=R3=R4=R5=1Ω。试用 网孔电流法求流过 R3 的电流。 3-6 应用网孔电流法求图 3-6 所示电路中的 ix。 题 3-5 图 题 3-6 图 3-7 应用网孔电流法求图 3-7 所示含受控源电路的各支路电流 I1,I2、,I3。 3-8 应用回路电流法求图 3-8 所示电路的各支路电流 I1, I2,I3。 Ⅲ Ⅱ 6Ω Ⅰ Ⅱ 8Ω 9V - + 2Ω 3Ω 5Ω I3 2Ω - + 15V 3Ω + - I2 21V I1 Ⅰ I4 1Ω 2Ω I5 Ⅲ 2Ω 12V + - I6 2Ω Ⅰ Ω I2 2Ω 2A I1 1V I3 I1 2A 1Ω I3 Ⅲ + - U 2Ω 22V + - I4 - + I2 Ⅱ 2Ω 1Ω 5A Ⅰ 1Ω4 I4 Ⅲ U - + 3 1 I5 0.5Ω Ⅱ