
第九章统计热力学初步 1.按照能量均分定律,每摩尔气体分子在各平动自由度上的平均动能为RT2。 现有1molC0气体于0℃、101.325kPa条件下置于立方容器中,试求: (1)每个C0分子的平动能8; (2)能量与此云相当的c0分子的平动量子数平方和(优+店+) 解:(1)c0分子有三个自由度,因此, E=3=3x8314x2735=5657x1024J 2L2×6.022×1023 (2)由三维势箱中粒子的能级公式 2 6=8ma++) 6-g =8×28.0104×5657x1021x8314×273.15)9 {6.6261x104×6.022×106101.325×103 =3.811×1020 2.2.某平动能级的+心+m)=45,使球该能级的统计权重。 解:根据计算可知,”、”,和”:只有分别取2,4,5时上式成立。因此,该能 级的统计权重为g=3引=6,对应于状态24s少254少42s少24sΨ42"s。 3.气体C0分子的转动惯量/=1.45×106kgm,试求转动量子数J为4与3 两能级的能量差△c,并求T=300K时的△ckT 解:假设该分子可用刚性转子描述,其能级公式为 6.626×10-4 8,=JJ+1)。h,△s=20-128×元2×145×106=3.077x10-2”J
第九章 统计热力学初步 1.按照能量均分定律,每摩尔气体分子在各平动自由度上的平均动能为 RT 2。 现有 1 mol CO 气体于 0 ºC、101.325 kPa 条件下置于立方容器中,试求: (1)每个 CO 分子的平动能 ; (2)能量与此 相当的 CO 分子的平动量子数平方和 ( ) 222 x y y nnn + + 解:(1)CO 分子有三个自由度,因此, 21 23 3 3 8.314 273.15 5.657 10 J 2 2 6.022 10 RT L − = = = (2)由三维势箱中粒子的能级公式 ( ) ( ) 2 222 2 2 3 2 2 3 222 2 2 2 2 3 21 2 3 34 26 20 8 8 8 8 8 28.0104 5.657 10 1 8.314 273.15 101.325 10 6.6261 10 6.022 10 3.811 10 x y z x y z h nnn ma ma mV m nRT nnn h h h p − = + + + + = = = = = 2. 2.某平动能级的 ( ) 45 2 2 2 nx + ny + nz = ,使球该能级的统计权重。 解:根据计算可知, x n 、 y n 和 z n 只有分别取 2,4,5 时上式成立。因此,该能 级的统计权重为 g = 3! = 6,对应于状态 245 254 425 245 452 , , , , 542 。 3.气体 CO 分子的转动惯量 46 2 =1.4510 kg m − I ,试求转动量子数 J 为 4 与 3 两能级的能量差 ,并求 T = 300 K 时的 kT 。 解:假设该分子可用刚性转子描述,其能级公式为 ( ) ( ) 3.077 10 J 8 1.45 10 6.626 10 , 20 12 8 1 2 2 2 4 6 3 4 2 2 − − − = = + = − I h J J J

3.077×10-22 k730x13807×1023=7.429x10 4.三维道振子的能级公式为6)-+》 ,式中s为量子数,即 5=,+,+,=0,12,3….试证明能级(6)的统计权重6)为 g同)=)6+2%+1) 解:方法1,该问题相当于将s个无区别的球放在x,:三个不同盒子中,每个盒 子容纳的球数不受限制的放置方式数。 ×盒中放置球数0,y,z中的放置数s+1 x盒中放置球数1,y,z中的放置数s ×盒中放置球数s,y,z中的放置数1 86)-=2=6+6+2) 方法二,用“,和:构成一三维空间,+,+=5为该空间的一个 平面,其与三个轴均相交于。该平面上”,,和:为整数的点的总数即 为所求问题的解。这些点为平面 g,=%,,=,=%,%,川,%=01,2,…在平面,++=5上的交 点: 由图可知, gs)=1+2+…+s+1 26+26+0
2 22 7.429 10 300 1.3807 1023 3.077 10 − − = = kT 4.三维谐振子的能级公式为 (s) s h = + 2 3 ,式中 s 为量子数,即 s = v x + v y + v z = 0,1, 2, 3, 。试证明能级 (s) 的统计权重 g(s) 为 ( ) ( 2)( 1) 2 1 g s = s + s + 解:方法 1,该问题相当于将 s 个无区别的球放在 x,y,z 三个不同盒子中,每个盒 子容纳的球数不受限制的放置方式数。 x 盒中放置球数 0,y, z 中的放置数 s + 1 x 盒中放置球数 1,y, z 中的放置数 s ………………………………………. x 盒中放置球数 s,y, z 中的放置数 1 ( ) ( 1)( 2) 2 1 1 1 = = + + + = g s j s s s j 方法二,用 z v ,v 和v x y 构成一三维空间, s v x + v y + v z = 为该空间的一个 平面,其与三个轴均相交于 s。该平面上 z v ,v 和v x y 为整数的点的总数即 为所求问题的解。这些点为平面 v x = n2 , v y = n2 , v z = n3 , n1 ,n1 ,n1 = 0,1, 2, 在平面 s v x + v y + v z = 上的交 点: 由图可知, ( ) ( 2)( 1) 2 1 1 2 1 + + = + + + + s s g s s

6.计算上题中各种能级分布拥有的微态数及系统的总微态数。 解:对应于分布”血%,上}的微态数,上述各分布的微态数分别为 1 I IV Total 3 6 3 3 15 10在体积为/的立方形容器中有极大数目的三维平动子其:/8m/p=0.1kT 式计算该系统在平衡情况下,:+,+)14的平动能级上粒子的分布数刀 与基态能级的分布数”之比。 解:根据Boltzmann分布 只-是epe-6ry号p1Ixo1灯n 80 =0.33298 基态的统计权重8。=1,能级:+川+)=14的统计权重8=6(量子 数1,2,3),因此 元-0329x6=197 11.若将双原子分子看作一维谐振子,则气体HC1分子与12分子的振动能级间 隔分别是5.94×10-0J和0.426×10-0J。试分别计算上述两种分子在相邻振 动能级上分布数之比。 解:谐振子的能级为非简并的,且为等间隔分布的 5.409x10-2 for HC L=eXp(△E/kT)= 0.3553forl2
6.计算上题中各种能级分布拥有的微态数及系统的总微态数。 解:对应于分布 n n n { 1, 2 ,L } 的微态数,上述各分布的微态数分别为 I II III IV Total 3 6 3 3 15 10.在体积为 V 的立方形容器中有极大数目的三维平动子,其 h 8mV 0.1kT 2 3 2 = , 式计算该系统在平衡情况下, ( ) 14 2 2 2 nx + ny + nz = 的平动能级上粒子的分布数 n 与基态能级的分布数 0 n 之比。 解:根据 Boltzmann 分布 ( ) 0 0 0 0 0 0.3329 exp exp 11 0.1 g g k T k T g g k T g g n n = = − − = − 基态的统计权重 g0 = 1 ,能级 ( ) 14 2 2 2 nx + ny + nz = 的统计权重 g = 6 (量子 数 1,2,3),因此 0.3329 6 1.997 0 = = n n 11.若将双原子分子看作一维谐振子,则气体 HCl 分子与 I2 分子的振动能级间 隔分别是 5.94 10 J −20 和 0.426 10 J −20 。试分别计算上述两种分子在相邻振 动能级上分布数之比。 解:谐振子的能级为非简并的,且为等间隔分布的 ( ) = − = − + 2 7 1 0.3553 for I 5.409 10 for HCl exp k T n n j j
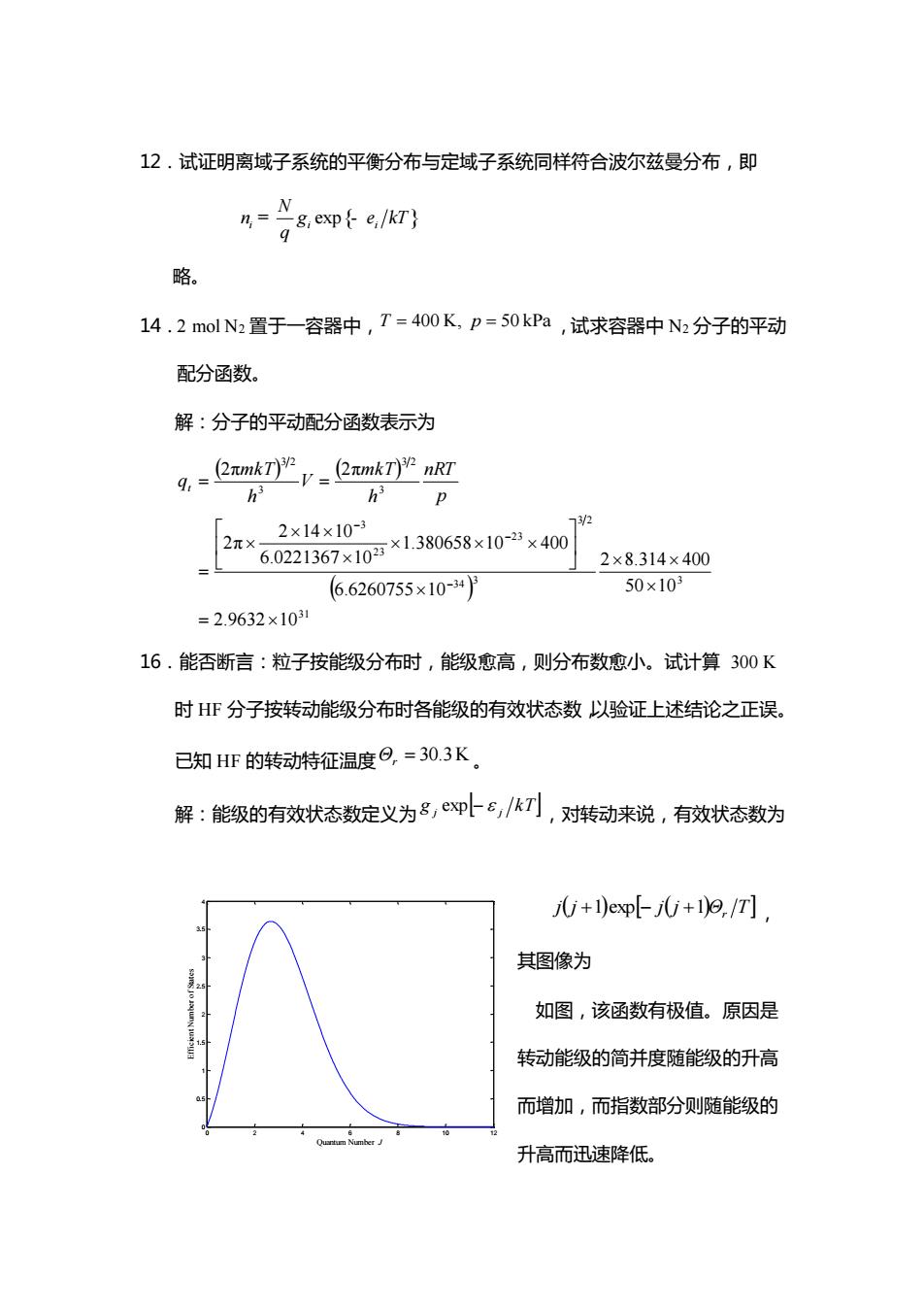
12.试证明离域子系统的平衡分布与定域子系统同样符合波尔兹曼分布,即 g8 expe,/ 略。 14.2molN2置于-容器中,T=400K,p=50kPa,试求容器中N2分子的平动 配分函数。 解:分子的平动配分函数表示为 2×14×10-3 V2 2×6021367X10=×1380658x10-×40 2×8.314×400 (6.6260755×10-4P 50×10 =2.9632×1031 16.能否断言:粒子按能级分布时,能级愈高,则分布数愈小。试计算300K 时HF分子按转动能级分布时各能级的有效状态数以验证上述结论之正误。 已知HF的转动特征温度⊙,=30.3K 解:能级的有效状态数定义为8,冲6,/k7,对转动来说,有效状态数为 j0+)ep[j0+9./T, 其图像为 如图,该函数有极值。原因是 转动能级的简并度随能级的升高 而增加,而指数部分则随能级的 升高而迅速降低
12.试证明离域子系统的平衡分布与定域子系统同样符合波尔兹曼分布,即 i i i exp{ } N n g T q = - e k 略。 14.2 mol N2 置于一容器中, T = 400 K, p = 50 kPa ,试求容器中 N2 分子的平动 配分函数。 解:分子的平动配分函数表示为 ( ) ( ) ( ) 3 1 3 3 3 4 3 2 2 3 2 3 3 3 3 2 3 3 2 2.9632 10 50 10 2 8.314 400 6.6260755 10 1.380658 10 400 6.0221367 10 2 14 10 2π 2π 2π = = = = − − − p nRT h mkT V h mkT qt 16.能否断言:粒子按能级分布时,能级愈高,则分布数愈小。试计算 300 K 时 HF 分子按转动能级分布时各能级的有效状态数,以验证上述结论之正误。 已知 HF 的转动特征温度 Θr = 30.3K 。 解:能级的有效状态数定义为 g kT j j exp − ,对转动来说,有效状态数为 j(j ) j(j )Θ T 1 r +1 exp − + , 其图像为 如图,该函数有极值。原因是 转动能级的简并度随能级的升高 而增加,而指数部分则随能级的 升高而迅速降低。 0 2 4 6 8 10 12 0 0.5 1 1.5 2 2.5 3 3.5 4 Quantum Number J Efficient Number of States

18.已知气体12相邻振动能级的能量差△5=0.426×102J,试求300K时h分 子的8,、9,、9及 架:分行的动特温度力如-加8架兰=05水 分子的振动配分函数为 1 1 ,“ea-e厅ew-e照 =0.9307 9=ep(e,/2T9.=0.9307ep(308.5/2×300) =1.557 f=g-1.557 19.设有N个振动频率为y的一维谐振子组成的系统,试证明其中能量不低于 的离子总数为Ncp人hkT)),其中v为振动量子数。 解:根据Boltzmann分布 n,=Nexp-cv)T) 9 ep-d/VAT)-ope) q j=v -exp(-h/2kT)N exp(-vhv/kT) g 1-exp(-hv/kT) Nexp(-vhv/kT) 23.N2与C0的相对分子质量非常接近,转动惯量的差别也极小,在25℃时振 动与电子运动均处于基态。但是N2的标准熵为191.6J·mol~.K-,而C0 的为197.6Jmo1K1,试分析其原因。 解:显然N2与C0标准熵的差别主要是由分子的对称性引起的:
18.已知气体 I2 相邻振动能级的能量差 0.426 10 J −23 = ,试求 300 K 时 I2 分 子的 Θv 、 v q 、 0 v q 及 0 v f 。 解:分子的振动特征温度为 , = 308.5 K = = = k k h h Θv 分子的振动配分函数为 0.9307 1 e e 1 2 2 308.5 2 300 308.5 2 300 = − = − = − − e e qv Θv T Θv T ( ) ( ) 1.557 exp 2 0.9307exp 308.5 2 300 0 = qv = Θr T qv = 1.557 0 0 f v = qv = 19.设有 N 个振动频率为 的一维谐振子组成的系统,试证明其中能量不低于 ( ) 的离子总数为 N exp(−vh kT) ,其中 v 为振动量子数。 解:根据 Boltzmann 分布 ( ( ) ) ( ( ) ) ( ) ( ) ( ) ( ) ( ) N ( h k T) h k T h k T q N h k T hj k T q N j k T h k T q N n q N k T n j v j j j j v v v v = − − − − = − = − = − − − = = = = exp 1 exp exp exp 2 exp exp 2 exp exp 23.N2 与 CO 的相对分子质量非常接近,转动惯量的差别也极小,在 25ºC 时振 动与电子运动均处于基态。但是 N2 的标准熵为 1 1 191.6 J mol K − − ,而 CO 的为 1 1 197.6 J mol K − − ,试分析其原因。 解:显然 N2 与 CO 标准熵的差别主要是由分子的对称性引起的:

AS=RIn 2=5.763J.mol-1.K-1 25.试由、6,-P导出理想气体服从p=N7 解:正则系综特征函数4=-kTnQ0N,V,),对理想气体 4--Qw..)T-MTha+krh N =-NkTIn g:-NkTIn(g,q,q.q)+kIn N! 只有平动配分函数与体积有关,且与体积的一次方程正比,因此: pV NkT 兰州交通大学物理化学教研组
1 1 ln 2 5.763 J mol K − − S = R = 25.试由 p V A T = − 导出理想气体服从 pV = NkT 解:正则系综特征函数 A = −kTln Q(N,V,T) ,对理想气体 ( ) ln ln( ) ln ! ln ln ! ! ln , , ln NkT q NkT q q q q k N NkT q k T N N q A k T Q N V T k T t r v e n N = − − + = − = − = − + 只有平动配分函数与体积有关,且与体积的一次方程正比,因此: pV NkT V NkT V q NkT V A T t T = = − = − ln 兰州交通大学 物理化学教研组