第二章热力学第一定律 2.5始态为25℃,200kPa的5mol某理想气体,经途径a,b两不同途径到达 相同的末态。途经a先经绝热膨胀到-28.47℃,100kPa,步骤的功 W=-557:再恒容加热到压力200kPa的末态,步骤的热么=25,42灯.途 径b为恒压加热过程。求途径b的成及A。 解:先确定系统的始、末 态 5 mol n=5 mol 1#5m01 1-298.15K 3=244.58K 1-200e =100 kPa 对于途径b,其功为 (PaP1J R=-5×8314×200×102×24458-29825) (10x1020×10=7.940d 根据热力学第一定律 四+只=网+Q, Q=M+2-=-5.57+25.42-(-7.940)=27.79k 2.64m01的某理想气体,温度升高20℃,求△H-△U的值
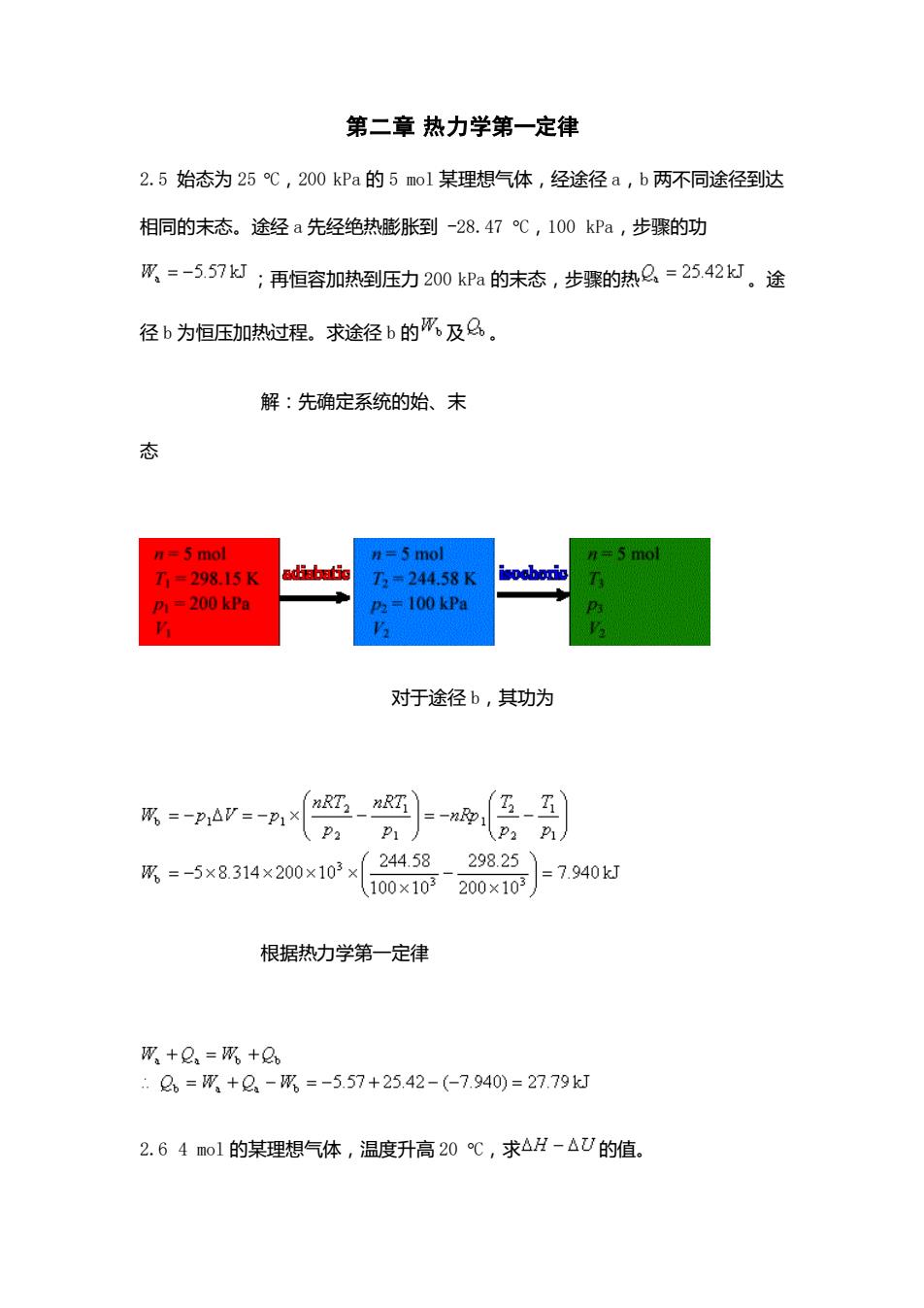
第二章 热力学第一定律 2.5 始态为 25 C,200 kPa 的 5 mol 某理想气体,经途径 a,b 两不同途径到达 相同的末态。途经 a 先经绝热膨胀到 -28.47 C,100 kPa,步骤的功 ;再恒容加热到压力 200 kPa 的末态,步骤的热 。途 径 b 为恒压加热过程。求途径 b 的 及 。 解:先确定系统的始、末 态 对于途径 b,其功为 根据热力学第一定律 2.6 4 mol 的某理想气体,温度升高 20 C,求 的值

解:根据焓的定义 H=U+pV :△H-△U=△(D) 而对理想气体pV=RT :△H-△U=△(nRT)=nR△T=4×8.314×20=665.12J 2.102m1某理想气体,C,a=7R2.由始态100kPa,50dm,先恒容加热 使压力体积增大到150dm,再恒压冷却使体积缩小至25d血2。求整个过程的 W,2,△U,△H 解:过程图示如下 n=2 mol n=2 mol P:=100 kPa P2200kP 1-0dm3 =50dm3 由于P巧=P乃巧,则3=Z,对有理想气体△H和 △U只是温度的函数 △H=△U=0 该途径只涉及恒容和恒压过程,因此计算功是方 便的
解:根据焓的定义 2.10 2 mol 某理想气体, 。由始态 100 kPa,50 dm3,先恒容加热 使压力体积增大到 150 dm3,再恒压冷却使体积缩小至 25 dm3。求整个过程的 。 解:过程图示如下 由于 ,则 ,对有理想气体 和 只是温度的函数 该途径只涉及恒容和恒压过程,因此计算功是方 便的

W=-P△/=-P3△/=-200×103×25×103-50×10-3) =5.00kJ 根据热力学第一定律 =A0-W=0-5.00=-5.00k 2.14容积为27m的绝热容器中有一小加热器件,器壁上有一小孔与100kP 的大气相通,以维持容器内空气的压力恒定。今利用加热器件使器内的空气由0 ℃加热至20℃,问需供给容器内的空气多少热量。已知空气的 Cv.m =20.4J.mol-1.R-1 假设空气为理想气体,加热过程中容器内空气的温度均匀。 解:在该问题中,容器内的空气的压力恒定,但物质量随温度 而改变 e=cur-器c.r e-r-6男 _100×103×2x204+8314xh29315 8.314 “27915=659d 注:在上述问题中不能应用C。,虽然容器的体 积恒定。这是因为,从 小孔中排出去的空气要对环境作功。所作功计算如下:
根据热力学第一定律 2.14 容积为 27 m3的绝热容器中有一小加热器件,器壁上有一小孔与 100 kPa 的大气相通,以维持容器内空气的压力恒定。今利用加热器件使器内的空气由 0 C 加热至 20 C,问需供给容器内的空气多少热量。已知空气的 。 假设空气为理想气体,加热过程中容器内空气的温度均匀。 解:在该问题中,容器内的空气的压力恒定,但物质量随温度 而改变 注:在上述问题中不能应用 ,虽然容器的体 积恒定。这是因为,从 小孔中排出去的空气要对环境作功。所作功计算如下:

在温度T时,升高系统温度dT, 排出容器的空气的物质量为 体积增量为d_灯dn=只d7 Po 所作功 wv=p小如9=号 这正等于用Ca和Cvm所计算 热量之差 2.15容积为0.1m的恒容密闭容器中有一绝热隔板,其两侧分别为0℃,4mo1 的Ar(g)及150℃,2mol的Cu(s)。现将隔板撤掉,整个系统达到热平衡,求 未态温度t及过程的△H。已知:Ar(g)和Cu(s)的摩尔定压热容C,m分别为 20,786Jm11K-1及24.435Jmo11,K1,且假设均不随温度而变。 解:图示如下 Ar(g Cu(s) Ar( 4mol o
在温度 T 时,升高系统温度 dT, 排出容器的空气的物质量为 所作功 这正等于用 和 所计算 热量之差。 2.15 容积为 0.1 m3的恒容密闭容器中有一绝热隔板,其两侧分别为 0 C,4 mol 的 Ar(g)及 150 C,2 mol 的 Cu(s)。现将隔板撤掉,整个系统达到热平衡,求 末态温度 t 及过程的 。已知:Ar(g)和 Cu(s)的摩尔定压热容 分别为 及 ,且假设均不随温度而变。 解:图示如下

假设:绝热壁与铜块紧密接触,且铜块的体积随 温度的变化可忽略不计 则该过程可看作恒容过程,因 (Ar.g)Cv.(Ar.g-t(Ar.g)]=n(Cu.s)Cv.(Cu.s)t(Cu.s)-t] n(Cu.s)Cy.(Cu,s)(Cu,s) n(Ar.gCv(Ar.g)+n(Cu.s)Cv.m (Cu.s) 2×24.435×150 -4×20786-8314+2×24557423C 假设气体可看作理想气体 Cra(Cu,s)Ca(Cu,,则 AH=n(Ar,g)C.A+n(Cu.sv.At' =4×20.784×(74.23-0)+2×24.435×150-74.23) =2.47k 2.18单原子理想气体A于双原子理想气体B的混合物共5mol,摩尔分数 为=04,始态温度了=40K,压力1=200Pa.今该混合气体绝热反抗恒外 压P=100Pa膨胀到平衡态。求末态温度3及过程的,△U,△H. 解:过程图示如下 A+B 3n albedlo n=3 mol =20 h=2m0 1-400 ntpu:=100 kPs A=2001P 100P
假设:绝热壁与铜块紧密接触,且铜块的体积随 温度的变化可忽略不计 则该过程可看作恒容过程,因 此 假设气体可看作理想气体, ,则 2.18 单原子理想气体 A 于双原子理想气体 B 的混合物共 5 mol,摩尔分数 ,始态温度 ,压力 。今该混合气体绝热反抗恒外 压 膨胀到平衡态。求末态温度 及过程的 。 解:过程图示如下

分析:因为是绝热过程,过程热力学能的变化等 于系统与环境间以功的形势所交换的能量。因此, △U=-Pp△V=CmA)+C,.Bh7 单子分子-0,双子分子8 资]眼小-动 g-+号6-剂 由于对理想气体/和H均只是温度的函数,所 华 △7-2a7-号×8314×63103-40)-548u △H=n,Ca)+m,C,a色T=2963103-40)=-8315过 2=0,W=△U=5.448k灯 2.19在一带活塞的绝热容器中有一绝热隔板,隔板的两侧分别为2mol,0℃ 的单原子理想气体A及5mo1,100℃的双原子理想气体B,两气体的压力均为 100kPa。活塞外的压力维持在100kPa不变。今将容器内的隔板撤去,使两种 气体混合达到平衡态。求末态的温度了及过程的?,△刀
分析:因为是绝热过程,过程热力学能的变化等 于系统与环境间以功的形势所交换的能量。因此, 单原子分子 ,双原子分子 由于对理想气体 U 和 H 均只是温度的函数,所 以 2.19 在一带活塞的绝热容器中有一绝热隔板,隔板的两侧分别为 2 mol,0 C 的单原子理想气体 A 及 5 mol,100 C 的双原子理想气体 B,两气体的压力均为 100 kPa。活塞外的压力维持在 100 kPa 不变。今将容器内的隔板撤去,使两种 气体混合达到平衡态。求末态的温度 T 及过程的
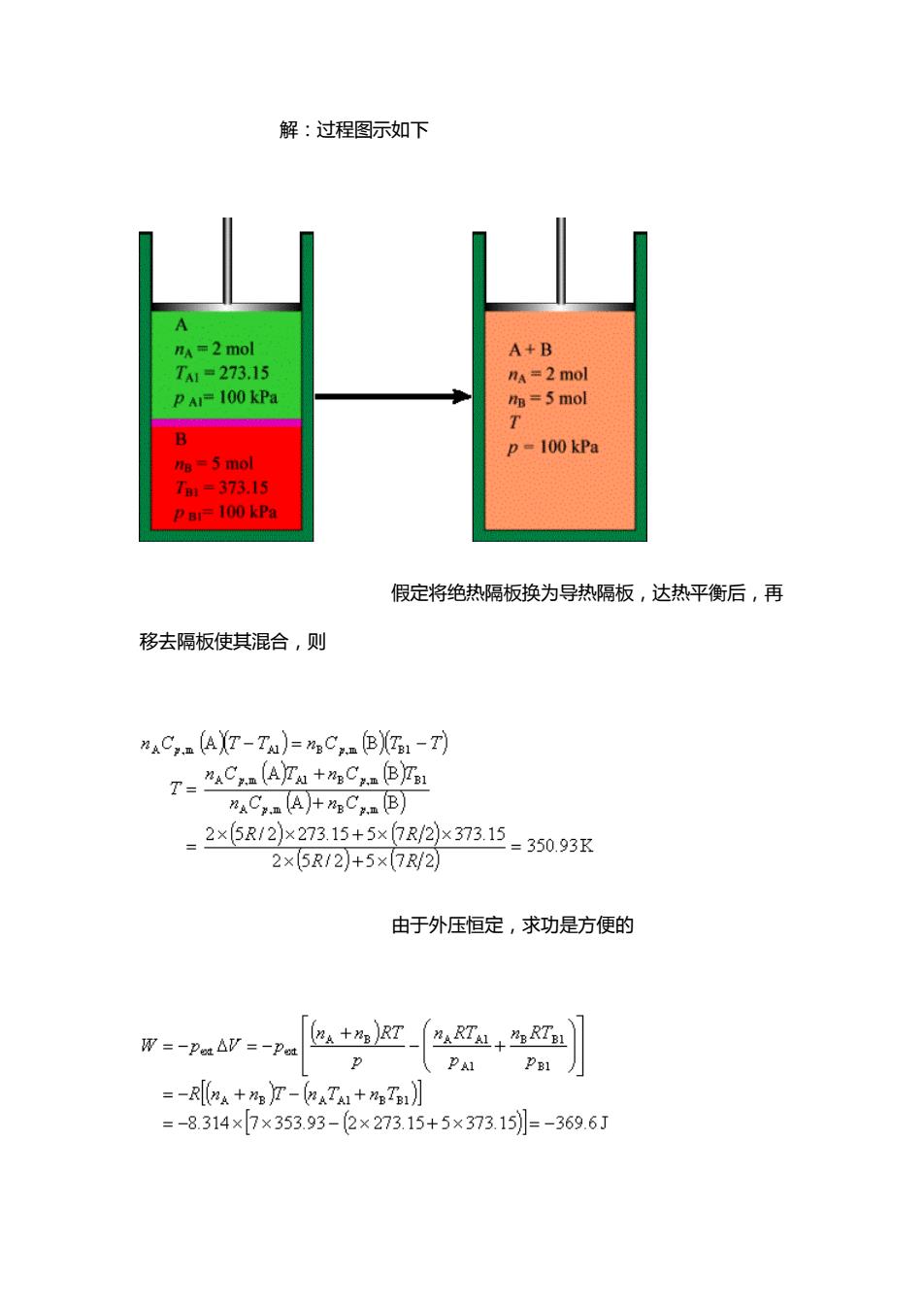
解:过程图示如下 m=2 mol A+B T=273.15 nA =2 mol pAl100kPa m=5 mol p-100 kPa a=5 mol 1.-373.15 Pai=100 kPa 假定将绝热隔板换为导热隔板,达热平衡后,再 移去隔板使其混合,则 nAC(AXT-TA)=mgC,(BXTI-T) T=aCaA2u+Ca®jr ”C.aA+C.aB) _2x5R/2x273.15+5xR2x373.15-350.93r 2×5R12)+5×7R2 由于外压恒定,求功是方便的 W=-PubV=-Pa 色+T-7丛+℃ PA1P1月 =-R[A+eT-(aTa1+TB1】 =-8.314×7×353.93-2×273.15+5×373.15]=-369.6J
解:过程图示如下 假定将绝热隔板换为导热隔板,达热平衡后,再 移去隔板使其混合,则 由于外压恒定,求功是方便的
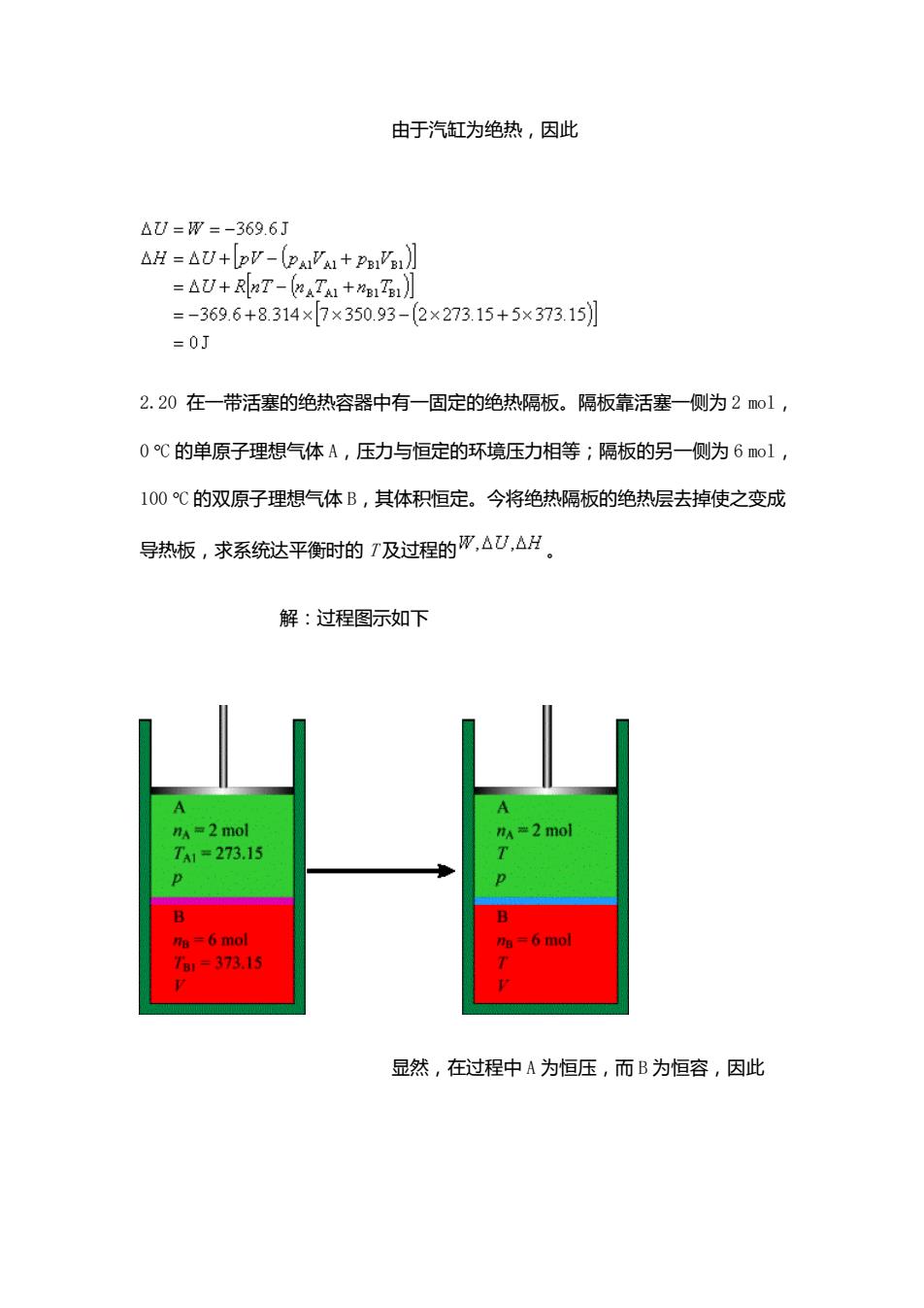
由于汽缸为绝热,因此 △U=W=-369.6J △H=AW+by-2u+P】 =△U+RnT-kTA1+1T1J =-369.6+8.314×7×350.93-(2×273.15+5×373.15] =0J 2.20在一带活塞的绝热容器中有一固定的绝热隔板。隔板靠活塞一侧为2m©l, 0℃的单原子理想气体A,压力与恒定的环境压力相等;隔板的另一侧为6l, 100℃的双原子理想气体B,其体积恒定。今将绝热隔板的绝热层去掉使之变成 导热板,求系统达平衡时的T及过程的,△,△H 解:过程图示如下 A=2m0 1273.11 1-37315 显然,在过程中A为恒压,而B为恒容,因此
由于汽缸为绝热,因此 2.20 在一带活塞的绝热容器中有一固定的绝热隔板。隔板靠活塞一侧为 2 mol, 0 C 的单原子理想气体 A,压力与恒定的环境压力相等;隔板的另一侧为 6 mol, 100 C 的双原子理想气体 B,其体积恒定。今将绝热隔板的绝热层去掉使之变成 导热板,求系统达平衡时的 T 及过程的 。 解:过程图示如下 显然,在过程中 A 为恒压,而 B 为恒容,因此

nC,.(A)T-TAI)=npCym (B)TB1-T) TCAumCr (B AC,.A)+CY.B) -2x5R/2x27315+6x5R237315-34815K 2×5R/2+6×5R/2 同上题,先求功 W=-Pabv--Pa P PA MART ARTAL =-%R7-7u=-2×8.314×48.15-273.15)=-1247k灯 同样,由于汽缸绝热,根据热力学第一定律 △U=W=-1.247k灯 △H=C,aA-TA)+C,aBT-Ti) =2×5R/2×348.15-273.15)+6×(7R/2)x348.15-373.14) =-1247kT 2.235mol双原子气体从始态300K,200kPa,先恒温可逆膨胀到压力为50kPa, 在绝热可逆压缩到末态压力200kPa。求末态温度T及整个过程的Q,W,△及 △H. 解:过程图示如下 5 mol 月=5m0 n=5 mol 73=300K =200kP Ps=50 kPa -200kp
同上题,先求功 同样,由于汽缸绝热,根据热力学第一定律 2.23 5 mol 双原子气体从始态 300 K,200 kPa,先恒温可逆膨胀到压力为 50 kPa, 在绝热可逆压缩到末态压力 200 kPa。求末态温度 T 及整个过程的 及 。 解:过程图示如下

要确定了,只需对第二步应用绝热状态方程 ,对双原子气体 因此 w =445.80 由于理想气体的/和H只是温度的函数, △U=mC,.G-T)=5×5R/2水445.8-30)=15.,15d △H=nC,mG-T)=5×(7R/2×445.8-300)=21.21J 整个过程由于第二步为绝热,计算热是方便的。 而第一步为恒温可逆 △1=0 :e=8=g=h2-知a会 -5834×30h-n29划 W=△U-Q=15.15-17.29=-2.14k 2.25一水平放置的绝热恒容的圆筒中装有无摩擦的绝热理想活塞,活塞左、右 两侧分别为50dm的单原子理想气体A和50dm'的双原子理想气体B。两气体均
要确定 ,只需对第二步应用绝热状态方程 ,对双原子气体 因此 由于理想气体的 U 和 H 只是温度的函数, 整个过程由于第二步为绝热,计算热是方便的。 而第一步为恒温可逆 2.25 一水平放置的绝热恒容的圆筒中装有无摩擦的绝热理想活塞,活塞左、右 两侧分别为 50 dm3的单原子理想气体 A 和 50 dm3的双原子理想气体 B。两气体均