
·第五章习题
◼第五章习题
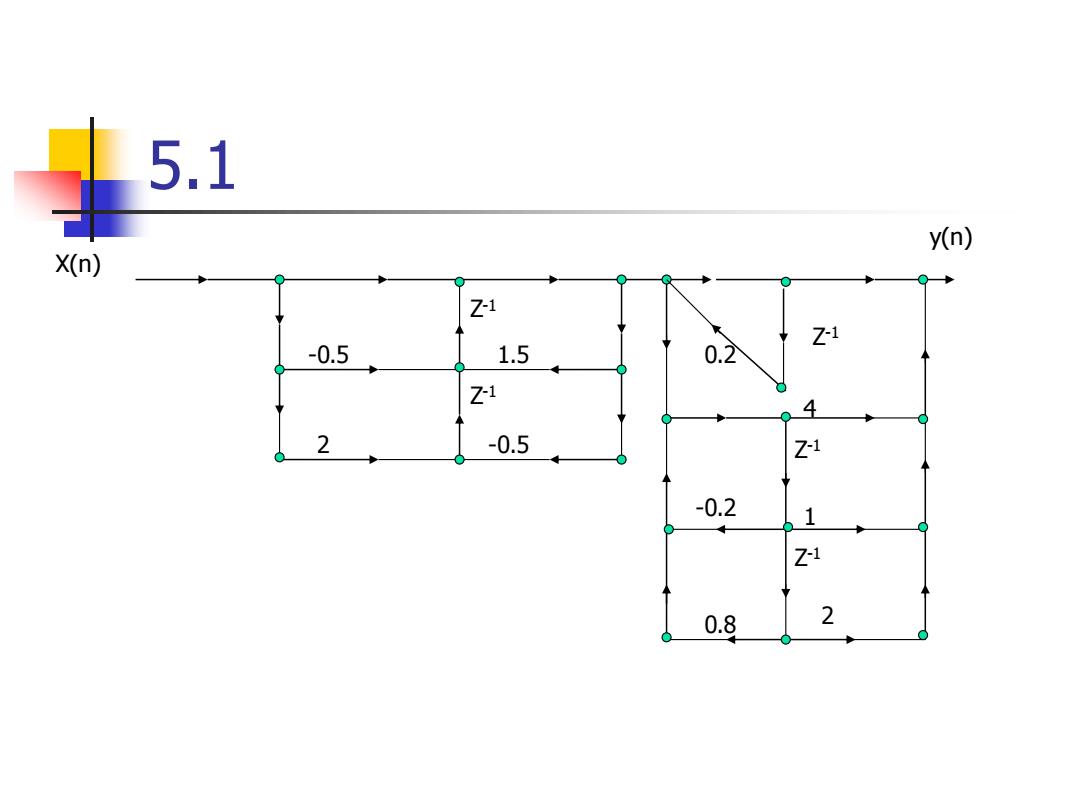
5.1 y(n) X(n) Z-1 Z-i -0.5 1.5 0.2 Z1 4 2 -0.5 Z-1 -0.2 1 Z-1 0.8 2
5.1 X(n) y(n) 1.5 -0.5 -0.5 2 41 2 -0.2 0.8 0.2 Z - 1 Z - 1 Z - 1 Z - 1 Z - 1

系统函数为 H( 1+0.5z1+2z2「 2 4+z1+2z 2 1-1.5e1-0.5e7×1+0.2z+ -0.2z1+0.8z2 6+4.4z1+16.5z2+5.1z3+7.8z4+0.8z5 1-1.5z+0.26z2-0.98z-3-0.62z4-0.08z5 由此得到相应的差分方程为 y(n)=6x(n)+4.4x(n-1)+16.5x(n-2) +5.1x(n-3)+7.8x(n-4)+0.8x(n-5) +1.5y(n-1)-0.26y(n-2)+0.98y(n-3) +0.62y(n-4)+0.08y(n-5)
0.62 ( 4) 0.08 ( 5) 1.5 ( 1) 0.26 ( 2) 0.98 ( 3) 5.1 ( 3) 7.8 ( 4) 0.8 ( 5) ( ) 6 ( ) 4.4 ( 1) 16.5 ( 2) 1 1.5 0.26 0.98 0.62 0.08 6 4.4 16.5 5.1 7.8 0.8 1 0.2 0.8 4 2 1 0.2 2 1 1.5 0.5 1 0.5 2 ( ) 1 2 3 4 5 1 2 3 4 5 1 2 1 2 1 2 1 1 2 + − + − + − − − + − + − + − + − = + − + − − + − − − + + + + + = − + + + + + − − + + = − − − − − − − − − − − − − − − − − − − y n y n y n y n y n x n x n x n y n x n x n x n z z z z z z z z z z z z z z z z z z z H z 由此得到相应的差分方程为 系统函数为

5.2 Z1 Z-i X(n) a b C Y(n)
5.2 X(n) Y(n) a b c Z - 1 Z - 1

证明:利用梅逊公式 e=∑r4 k 共有三条通路: T=cz2,T2 bz,T3 =a △=1 △1=1,△2=1,△2=1, H(z)=a+bz+cz-2
证明:利用梅逊公式 1 2 1 2 2 3 1 2 2 1 ( ) 1, 1, 1, 1 , , 1 ( ) − − − − = + + = = = = = = = = H z a bz cz T cz T bz T a H z T k k k 共有三条通路:
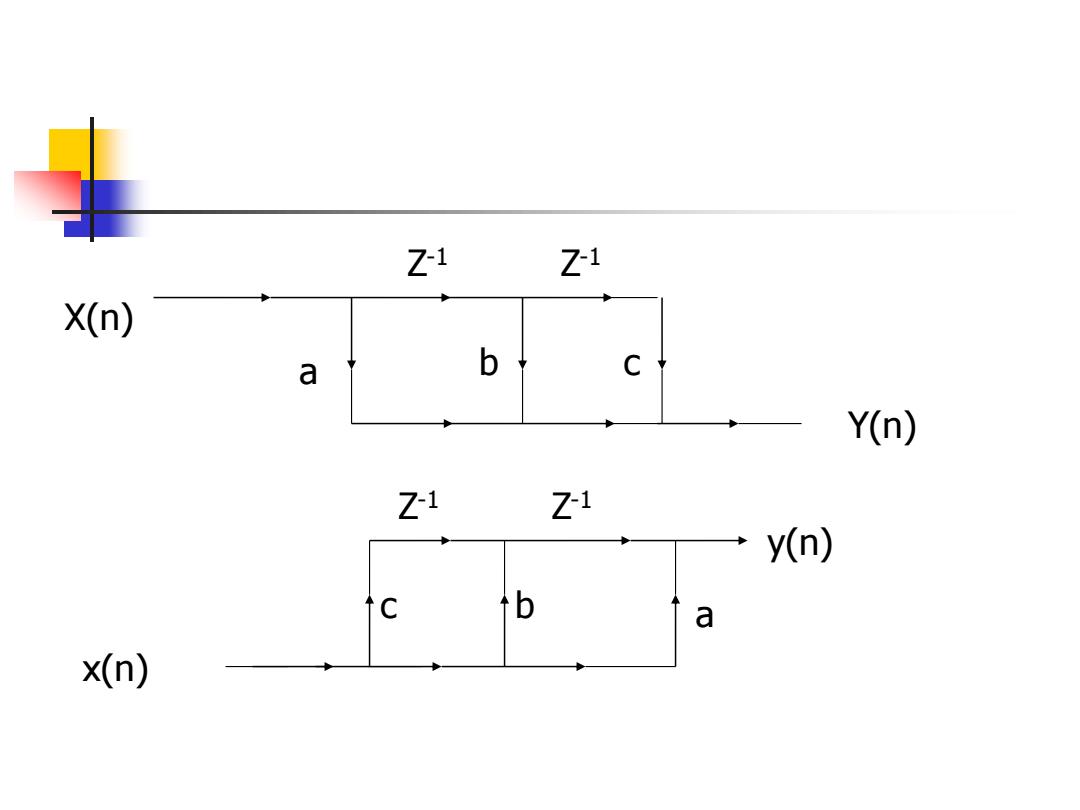
Z1 Z-i X(n) a b C Y(n) Z-i Z-i y(n) C b a x(n)
X(n) Y(n) a b c Z - 1 Z - 1 y(n) x(n) c b a Z - 1 Z - 1
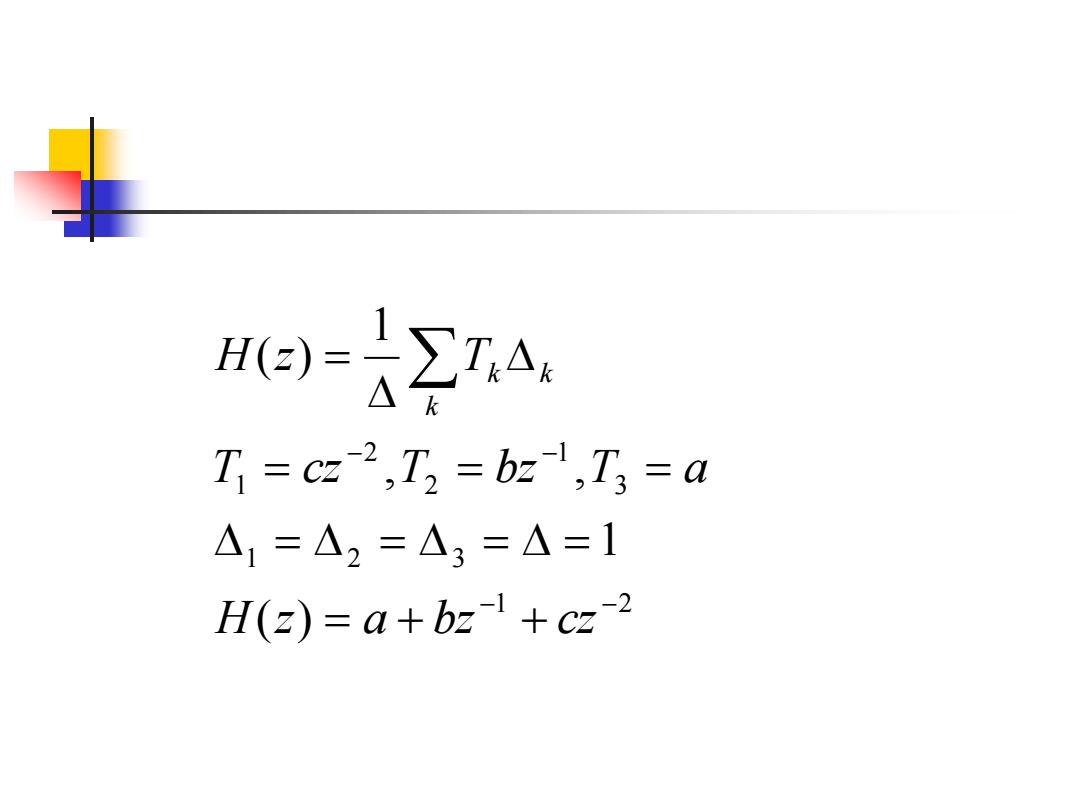
I3- k T=cz-2,T2 bz-,T3 a A1=△2=△3=△=1 H(z)=a+bz+cz-2
1 2 1 2 3 3 1 2 2 1 ( ) 1 , , 1 ( ) − − − − = + + = = = = = = = = H z a bz cz T cz T bz T a H z T k k k

5.5 差分方程 0=x00+0m-+30w-)+a-2 1+z H(z)= 122 直接1型: Y(n) X(n) Zi 2/3 Z-1 Z1 1/4
5.5 1 2 1 4 1 3 2 1 1 ( ) ( 2) 4 1 ( 1) 3 2 ( ) ( ) ( 1) − − − − − + = = + − + − + − z z z H z y n x n x n y n y n 差分方程 直接1型: Z -1 Z -1 Z -1 2/3 1/4 X(n) Y(n)
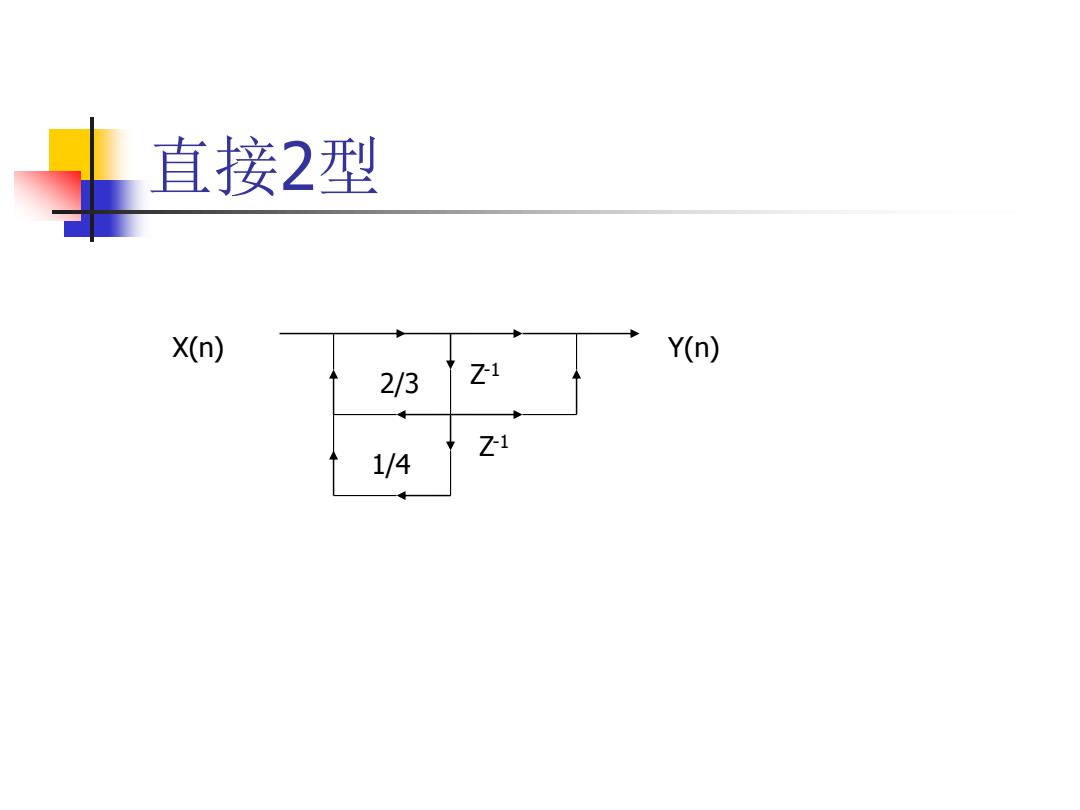
直接2型 X(n) Y(n) 2/3 Zi Zi 1/4
直接2型 Z -1 Z -1 2/3 1/4 X(n) Y(n)

全一阶节 系统函数 1+z H(z)= 1+z可 1- -4 2 (1-az)1-bz1) 3 2+6 2-13 a= 6 6 全一阶:H(e)= (1+z) 1 0-2+0-2 6 6 1 或H(z)= (1+z1) 2+80-2-9 6 6
全一阶节 ) 6 2 13 (1 (1 ) ) 6 2 13 (1 1 ( ) ) 6 2 13 (1 1 ) 6 2 13 (1 (1 ) ( ) 6 2 13 , 6 2 13 (1 )(1 ) 1 4 1 3 2 1 1 ( ) 1 1 1 1 1 1 1 1 1 1 2 1 − − − − − − − − − − − − − − + + − = − − + − + = − = + = − − + = − − + = z z z H z z z z H z a b az bz z z z z H z 或 全一阶: 系统函数