广东海洋大学：《数字信号处理 Digital Signal Processing》课程教学资源（作业习题）第二章 离散傅立叶变换与快速算法（习题及答案）

2.1 如果x()是一个周期为N的周期序列， 则它也是周期为2N的周期序列。 DFS(周期为N) DFS(周期为2N) x(n) → X (k),x(n) → X2(k) 根据题意： X()-空xm形，-是ne员 n=0 n=0

2.1   − = − − = = =   1 0 2 1 ~ 0 ~ ~ 1 ~ 2 ~ ~ DFS 2N) 1 ~ DFS N ) ~ X ( ) ( ) ( ) ( ) X ( ) ( ) X ( ) 2N ( ) N N n k N j N n n k N k x n W x n e x n k x n k x n  根据题意： ， 则它也是周期为 的周期序列。 如果 是一个周期为 的周期序列， （周期为 （周期为

2W-1 2W-1 X,(k)=∑x(n)W2N=∑x(n)wxk2 n=0 n=0 mm,s”+nw, 2W-1 = n=0 n=N W-1 2W-1 m)w2+∑(n)Wx2nn-N n=0 n=N mw,+觉n+Ng.: n=0 n=0 W ∑xn)wwk2+e∑xn)wwk2 -I n=0 n=0 =I+e)x,(吃 所以 2X.为偶数 0,k为奇数

     = + = + = + + + = + = = − − = − − = − = + − = = − − = − = − = − = − = − =           ， 为奇数 为偶数 ＝ 所以 ＝ 0 k ), 2 2X ( X ( ) ) 2 (1 )X ( ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) X ( ) ( ) ( ) ~ 1 ~ 2 ~ 1 1 0 / 2 1 ~ 0 / 2 ~ 1 0 ' ( ) / 2 1 ~ 0 / 2 ~ 2 1 / 2 1 ~ 0 / 2 ~ 2 1 / 2 1 ~ 0 / 2 ~ 2 1 0 / 2 2 1 ~ 0 2 ~ ~ 2 ' ' ' k k k k e x n W e x n W x n W x n N W x n W x n W x n W x n W k x n W x n W j k N n n k N j k N n n k N N n n N k N N n n k N n n N N n N n k N N n n k N N n N n k N N n n k N N n n k N N n n k N  

2.2 X(n) X(n-2) 0123 n 01234567n X(n) 0123 n

2.2 0 1 2 3 X(n) n X(n-2) n 0 1 2 3 4 5 6 7 X(n) n 0 1 2 3 ~

2.4 11110000 11110000 11110000 11111111 11111111 11111111 f(n) y(-m) 11111111 11111111 11111111 4 y(1-m) 11111111 11111111 11111111 4 2-m) 11111111 11111111 11111111 4 y3-m) 11111111 11111111 11111111 4 4-m) 11111111 11111111 11111111 4 y(5-m) 11111111 11111111 11111111 4 (6-m) 11111111 11111111 11111111 4 y(7-m) 11111111 11111111 11111111 4

2.4 x(m) 11110000 11110000 11110000 y(m) 11111111 11111111 11111111 f(n) y(-m) 11111111 11111111 11111111 4 y(1-m) 11111111 11111111 11111111 4 y(2-m) 11111111 11111111 11111111 4 y(3-m) 11111111 11111111 11111111 4 y(4-m) 11111111 11111111 11111111 4 y(5-m) 11111111 11111111 11111111 4 y(6-m) 11111111 11111111 11111111 4 y(7-m) 11111111 11111111 11111111 4 ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

v f(n) ●

~ f(n)

)=冕fow=42e受，k=012N-l V- 一j 1a0 n=0 2元Nk 1-e 4N,k=0,m为任意整数 =4× =41-ev 1-e 1-e停0，其它 rk+mN2/mggw=是/aw N-I n=0 n=0 所以，时域上周期序列的离散傅里叶级数在 频域上仍是周期序列 4N,k=mN,m整数 Fk)=0, 其它

   = = + =    = = − − = − − =  = = = −     − = − = − − − − − = − − = ，其它 整数 频域上仍是周期序列 所以，时域上周期序列的离散傅里叶级数在 ＝ 其它 ， 为任意整数 ， （ ＋ 0 4 , , ( ) ( ) ( ) ( ) 0, 4 , 0 1 1 4 1 1 4 ( ) ( ) 4 0,1,2.... 1 ~ 1 0 1 0 N ) 2 2 2 2 1 0 1 2 0 N k m N m F k F k m N f n W f n W N k m e e e e F k f n W e k N N n n k N N n n k m N k N j j k k N j Nk N j N n n k N j N n n k N     

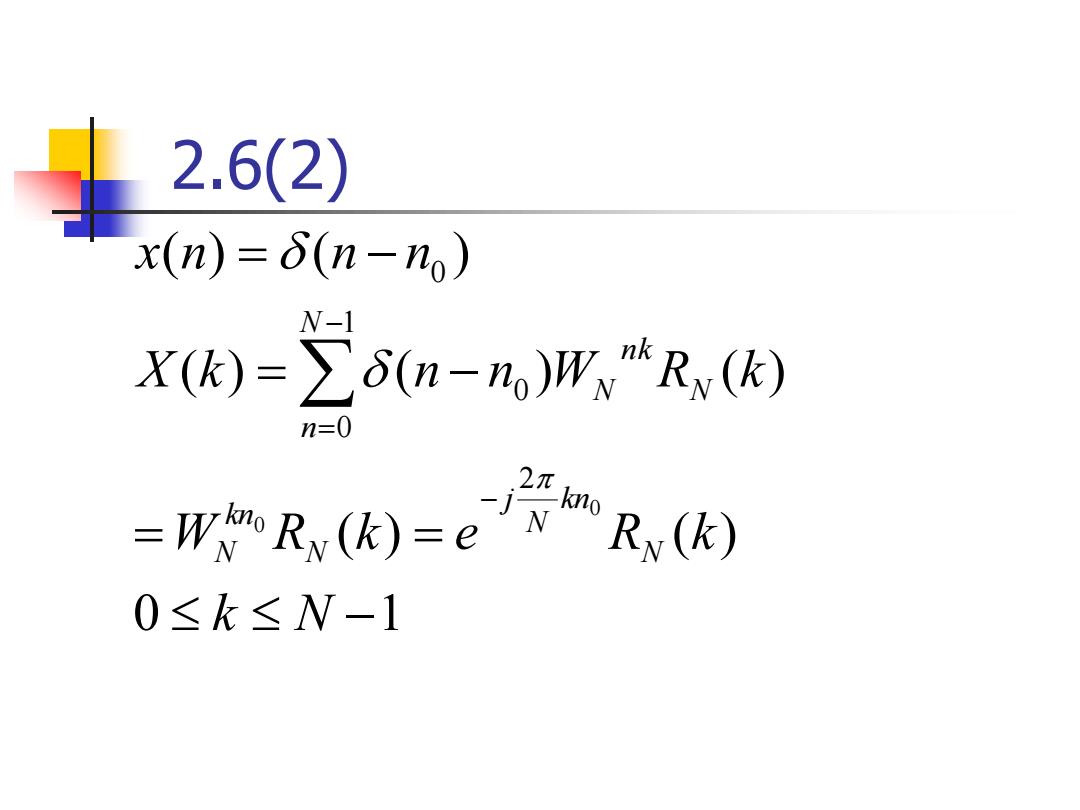
2.6(2) x(n)=δ(n-n) N-1 X(k)=∑δ(n-n)W,Rx(k) n=0 =Wino Rx(k)=e 、"R因) 0≤k≤W-1

2.6(2) 0 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 0 2 1 0 0 0   − = = = − = − − − =  k N W R k e R k X k n n W R k x n n n N kn N j N kn N N N n n k N   

2.9 y(-mily(a(o)(n(5(6(010lom)m) X(m) 苏型--00 f(0)=1 f(7)=-1 f(n) f(1)=2 f(8)=-3 f2)-3 65-43-20BA店6五89 f3)=4 0=4 f(4)=5 111 f(11)=-3 f(5)=3 f(12)=-2 f(6)=1 f13)=-1

2.9 0 1 2 3 4 5 6 7 8 9 X(m) 0 1 2 3 4 5 6 7 8 9 y(m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(-m) f(0)=1 9 -8-7 -6 -5 -4-3 -2- 1 0 y(-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(1-m) f(1)=2 f(2)=3 f(3)=4 f(4)=5 f(5)=3 f(6)=1 f(7)=-1 f(8)=-3 f(9)=-5 f(10)=-4 f(11)=-3 f(12)=-2 f(13)=-1 9 -8-7 -6 -5 -4-3 -2- 1 0 y(2-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(3-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(4-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(5-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(6-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(7-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(8-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(9-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(10-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(11-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(12-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(13-m) 9 -8-7 -6 -5 -4-3 -2- 1 0 y(14-m) f(n)

2.10 =*a=2ma-am-艺ex2mjsn（2u-m m=0 2m -j π 2(n-m) N"te N"e n 2(n-m) - -e N 47 2π 2 。(m-2m）N(m-2m） te -e Ne N-e 2π 一j n -2(m-2m） 2元(n-2m) te 3x π -e π j )- e N-1 2死2m e N-1 2π2m e e Aj m=0 Aj m=0 2π 2π 2π -iN"1-e 2元2N 22N - e e 1-e -e 4i e 2 2π2 1-eN Aj 1-e N N 2π 2 - -n 2π e -e 41 42s 4 N 2π sin( 2

) 2 sin( 2 )) 2 (2 sin( 4 ( ) 4 1 1 4 1 1 4 ( ) 4 4 4 ( ) 4 1 ( ) 4 1 ( ) 4 1 ( )( ) 4 1 ( ) 2 )sin 2 ( ) ( ) ( ) ( ) ( ) cos( 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 0 2 2 2 1 0 2 2 2 1 0 2 2 ( 2 ) 1 2 0 ( 2 ) 2 2 2 2 ( 2 ) 1 2 0 ( 2 ) 2 2 ( ) 2 ( ) 1 2 2 0 2 1 0 1 0 n N N n N j j N e e j N e e j e e e j e e e j N e j e e j e e e j e e e e j e e e e j e e e e j n m N m N f n x n y n x m y n m n N n j N j N j N N n j N j N j N N n j N j n N n j N j N m m N j n N j N m m N j n N j N m n N n j N j n m N j N m n m N n j N n j N j n N n m j N j N m n m N n j N j n m N n m j N m j N j N m m N j N m N m                                 = = − = − − + − − = − − = − − + = − − + = − + − = + −       =  = − = − − − − − − − = − − = − − = − − − = − − − − − − = − − − − − − − = − = − =         2.10

()x(cos 2元 -j n)e n=0 n=0 - 2nk N 1 2π 2 -+e) 2 2πN(1-k) 1 1-e 1-e 2rN(1+k) 2 1-e 1-e 2元(1+k) N,k三y N,k=N-1 2 0,其它

         = − = =           − − + − − = = + = + = = − + − + − − − = − − + − = − − − = − − =     0,其它 , 1 2 1 , 1, 2 1 1 1 1 1 2 1 ( ) 2 1 ( ) 2 1 ) 2 ( ) ( ) cos( (1 ) 2 (1 ) 2 (1 ) 2 (1 ) 2 1 0 (1 ) 2 (1 ) 2 1 0 2 2 2 1 0 1 2 0 N k N N k e e e e e e e e e n e N X k x n W k N j N k N j k N j N k N j N n n k N n k j N j N n n k N n j N n j N j N n n k N j N n n k N           