
第6章 信息论基础 6.5信道模型和信道容量
第 6 章 信息论基础 6.5 信道模型和信道容量

信道容量和信道编码 回顾 M元调制产生的信号波形 ●用M=2k个信号波形,每个波形传递k比特信息。 ●M→oo时,只要≥-1.6dB ,可借助正交的信号波形使 差错概率任意小。 ●带宽W=Mf随k增加而指数增加。信道带宽利用率太低! 编码波形 (由二进制或非二进制序列产生的信号波形) ·W仅随k的增加而线性增加。更具有潜力获得较高带宽效率。 ·在功率受限系统(R/WK1)和带宽受限系统(R/W>1)中都 具有优越性能。 2
2 ⚫ W仅随 k 的增加而线性增加。更具有潜力获得较高带宽效率。 ⚫用 M=2k 个信号波形,每个波形传递 k 比特信息。 ⚫ ,可借助正交的信号波形使 差错概率任意小。 M dB → − 1.6 时,只要 b 回顾 ⚫带宽 W=Mf 随k 增加而指数增加。信道带宽利用率太低! 编码波形 (由二进制或非二进制序列产生的信号波形) ⚫在功率受限系统( R/W1 )中都 具有优越性能。 M元调制产生的信号波形 信道容量和信道编码
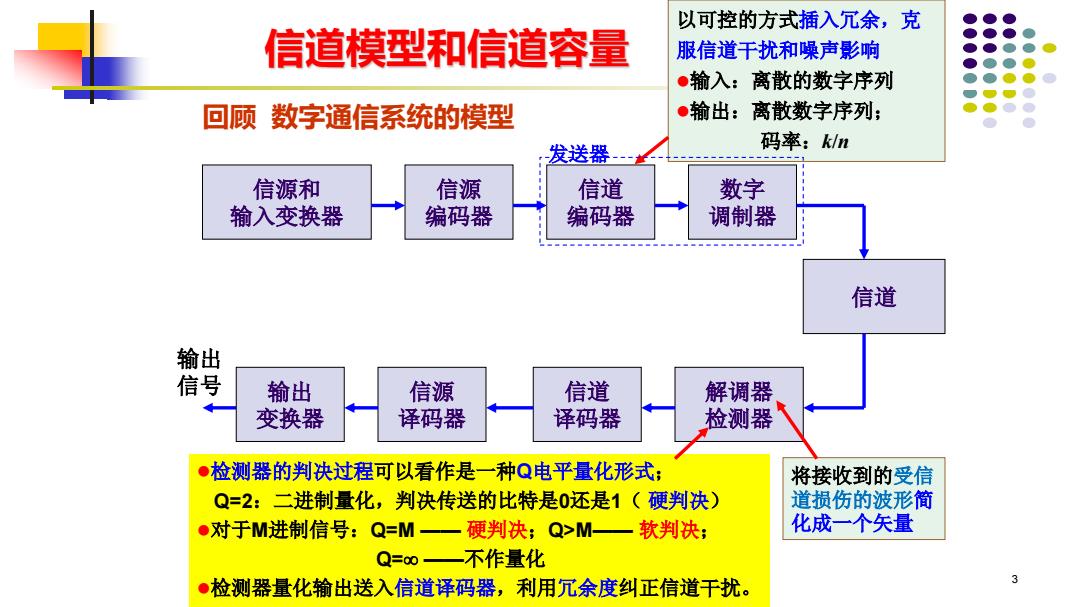
以可控的方式插入冗余,克 信道模型和信道容量 服信道干扰和噪声影响 ●输入:离散的数字序列 回顾数字通信系统的模型 ●输出:离散数字序列; 发送器 码率:kn 信源和 信源 信道 数字 输入变换器 编码器 编码器 调制器 信道 输出 信号 输出 信源 信道 解调器 变换器 译码器 译码器 检测器 ●检测器的判决过程可以看作是一种Q电平量化形式; 将接收到的受信 Q=2:二进制量化,判决传送的比特是0还是1(硬判决) 道损伤的波形简 ●对于M进制信号:Q=M—一硬判决;Q>M一软判决; 化成一个矢量 Q=0一不作量化 ●检测器量化输出送入信道译码器,利用冗余度纠正信道干扰。 3
3 信源和 输入变换器 信源 编码器 信道 信源 译码器 数字 调制器 信道 编码器 解调器 检测器 信道 译码器 输出 信号 输出 变换器 以可控的方式插入冗余,克 服信道干扰和噪声影响 ⚫输入:离散的数字序列 ⚫输出:离散数字序列; 码率:k/n 将接收到的受信 道损伤的波形简 化成一个矢量 ⚫检测器的判决过程可以看作是一种Q电平量化形式; Q=2:二进制量化,判决传送的比特是0还是1( 硬判决) ⚫对于M进制信号:Q=M —— 硬判决;Q>M—— 软判决; Q= ——不作量化 ⚫检测器量化输出送入信道译码器,利用冗余度纠正信道干扰。 回顾 数字通信系统的模型 信道模型和信道容量 发送器

6.5信道模型和信道容量 4
4 6.5 信道模型和信道容量

信道模型和信道容量 编码设计时常用的信道模型 可用以下三个参数来描述通信信道: ●信道的输入信号集(输入符号集)X ●信道的输出信号集(输出符号集)Y ●输入、输出序列(任意长度)关系的条件概率:P(,y2,Lynx,x2,Lxn) 如果对于所有: Pylx)=ΠPOy,Ix) i=l 则称信道是无记忆的。(i时刻的输出仅取决于i时刻的输入)
5 1 ( | ) ( | ) n i i i P y x P y x = = 编码设计时常用的信道模型 可用以下三个参数来描述通信信道: 信道模型和信道容量 1 2 1 2 ( , , | , , ) ⚫输入、输出序列(任意长度n)关系的条件概率 P y y y x x x L L n n : ⚫信道的输入信号集 (输入符号集)X ⚫信道的输出信号集 (输出符号集)Y 如果对于所有n: 则称信道是无记忆的。(i 时刻的输出仅取决于i 时刻的输入)
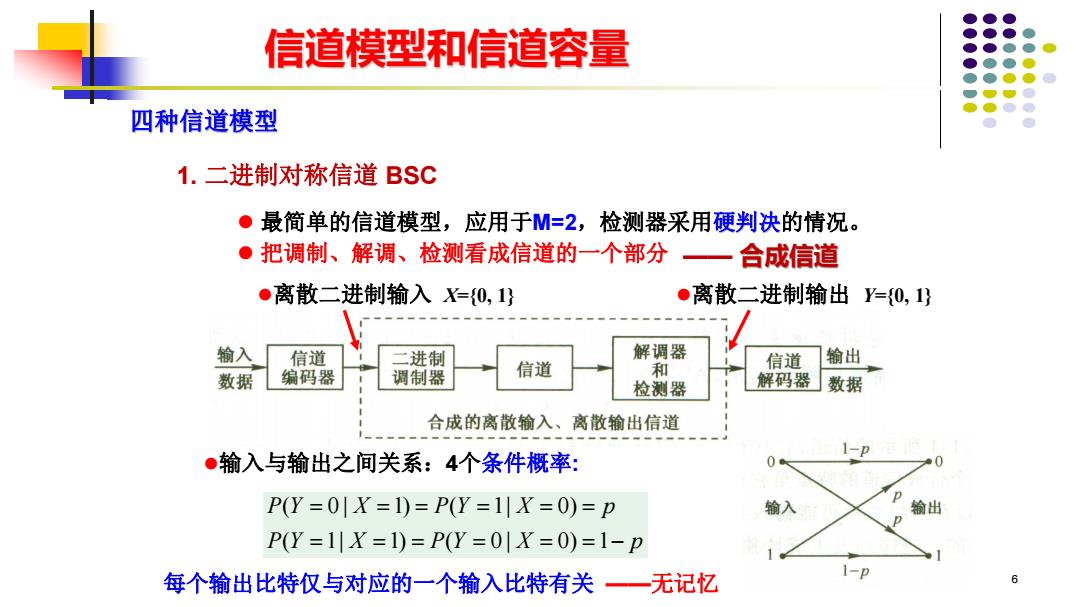
信道模型和信道容量 四种信道模型 1.二进制对称信道BSC ·最简单的信道模型,应用于M=2,检测器采用硬判决的情况。 。把调制、解调、检测看成信道的一个部分一 合成信道 ●离散二进制输入X={0,1} ●离散二进制输出Y={0,1} 输入 信道 二进制 解调器 信道 和 信道 输出 数据 编码器 调制器 检测器 解码器 数据 合成的离散输入、离散输出信道 ●输入与输出之间关系:4个条件概率: PY=0|X=1)=P(Y=1|X=O)=p 输H P(Y=1X=1)=P(Y=01X=0)=1-p 每个输出比特仅与对应的一个输入比特有关一无记忆 6
6 ⚫ 最简单的信道模型,应用于M=2,检测器采用硬判决的情况。 ⚫ 把调制、解调、检测看成信道的一个部分 ( 0 | 1) ( 1| 0) ( 1| 1) ( 0 | 0) 1 = = = = = = = = = = = = − P Y X P Y X p P Y X P Y X p 四种信道模型 1. 二进制对称信道 BSC —— 合成信道 ⚫输入与输出之间关系:4个条件概率: 信道模型和信道容量 ⚫离散二进制输入 X={0, 1} ⚫离散二进制输出 Y={0, 1} 每个输出比特仅与对应的一个输入比特有关 ——无记忆

信道模型和信道容量 2.离散无记忆信道DMC BSC推广一广义的离散输入、离散输出信道 图7-1-3离散g进制输人、Q进制输出信道 ●离散输入M元符号 ●Q电平离散输出 Q≥M=29 输入 信道 M元 解调器 信道 输出 和 数据 编码器 调制 信道 检测器 解码器」数据 检测器软判快 合成的离散输入、离散输出信道 ●合成信道的输入输出特性(信道和调制是无记忆时),用MQ个条件概率描述: P(Y=X=x)=P(ylx,) i=0,1,.2-1 j=0,1,.M-1 输入序列X、输出序列Y的联合概率: P(Y=V:Y =VL Y=VIX=u,X2 =4L X,=u)=IIP(Y =VIX=ug) 无记忆条件 k=l 条件概率P心U)可以表示成矩阵形式P=P,称为信道的转移概率矩阵
7 ( | ) ( | ) i j i j P Y = y X = x = P y x 2. 离散无记忆信道 DMC 输入序列X 、输出序列Y 的 联合概率: 1 1 2 2 1 1 2 2 1 ( , | , ) ( | ) = = = = = = = = = = n n n n n k k k k k P Y v Y v Y v X u X u X u P Y v X u L L i = 0, 1, … Q-1 j = 0, 1, … M-1 无记忆条件 条件概率P(yi |xj )可以表示成矩阵形式 P =[pij],称为信道的转移概率矩阵。 信道模型和信道容量 q ⚫离散输入M元符号 ⚫Q电平离散输出 Q M = 2 BSC推广——广义的离散输入、离散输出信道 ⚫合成信道的输入输出特性(信道和调制是无记忆时),用MQ个条件概率描述: 检测器软判决 M元 调制

信道模型和信道容量 3.离散输入、连续输出信道 调制器输入信号为离散字符,检测器的输出未经量化。 ·离散输入X ●连续输出Y 输入 信道 二进制 解调器 信道 输出 数据 编码器 调制器 信道 和 检测器 解码器 数据 合成的离散输入、离散输出信道 ●一组条件概率密度函数:P(y|X=x) x∈X,y∈R 例:AWGN信道: Y=X+N N:零均值,方差为σ2的高斯随机变量 P(y川X=x)= e-0-x212o2 √2πo ■对于任意给定的输入序列X,相应的输出序列y=X+N: i=1,2,..n 信道为无记忆的条件为: P(y,y2L yx,x2L x)=IP(y;lx,) 8 i=l
8 3. 离散输入、连续输出信道 调制器输入信号为离散字符,检测器的输出未经量化。 ⚫一组条件概率密度函数:P( y | X = x ) 例:AWGN信道: Y X N = + 2 2 1 ( ) / 2 ( | ) 2 − − = = y x P y X x e 1 2 1 2 1 ( , | , ) ( | ) = L L = n n n i i i 信道为无记忆的条件为: P y y y x x x P y x 信道模型和信道容量 ⚫离散输入 X ⚫连续输出Y N:零均值,方差为 2 的高斯随机变量 ◼对于任意给定的输入序列 Xi,相应的输出序列 Yi =Xi +Ni i=1,2,…n x X y R
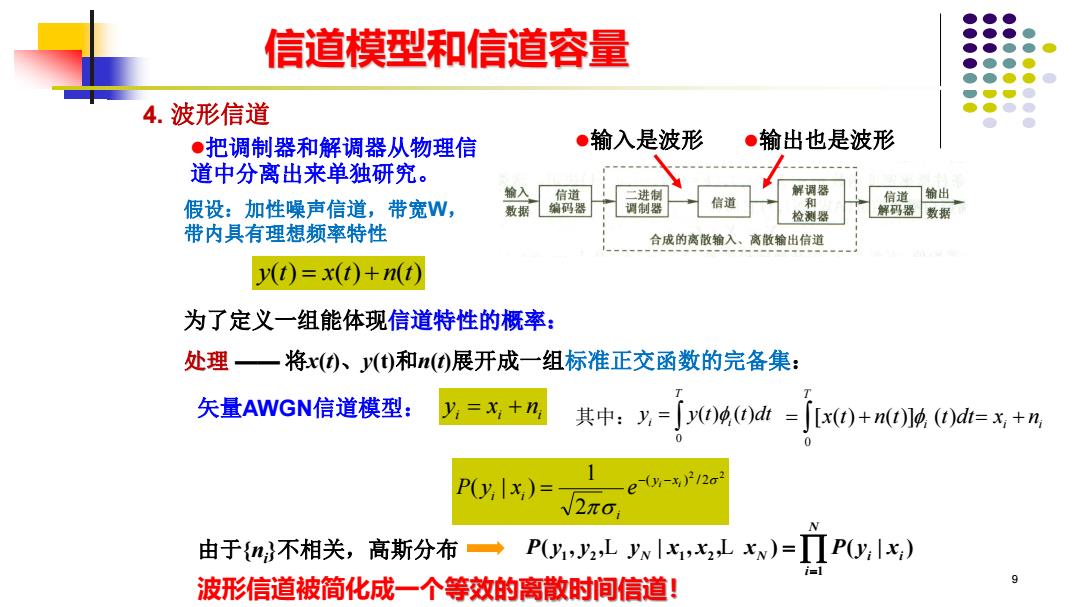
信道模型和信道容量 4.波形信道 ·把调制器和解调器从物理信 ●输入是波形 ●输出也是波形 道中分离出来单独研究。 输入 信道 二进 解调器 信道 信道 输出 假设:加性噪声信道,带宽W, 数据 编码器 调制器 检测器 解码器」数据 带内具有理想频率特性 合成的离散输入、离散输出信道 y(t)=x(t)+n(t) 为了定义一组能体现信道特性的概率: 处理一将x(、y()和n()展开成一组标准正交函数的完备集: 矢量AWGN信道模型: y=x+n 其中:y=∫0)()d=jx0)+nA)d=x+n P(yx)= e(0y-x)212a N2π, 由于{}不相关,高斯分布◆ PLw)-iPo1x) 波形信道被简化成一个等效的离散时间信道! 9
假设:加性噪声信道,带宽W, 带内具有理想频率特性 9 y t x t n t ( ) ( ) ( ) = + 4. 波形信道 ⚫把调制器和解调器从物理信 道中分离出来单独研究。 将x(t)、y(t)和n(t)展开成一组标准正交函数的完备集: 0 ( ) ( ) T i i y y t t dt = i i ni y = x + 1 2 1 2 1 ( , , | , , ) ( | ) N N N i i i P y y y x x x P y x = L L = 2 2 ( ) / 2 2 1 ( | ) i i y x i i i P y x e − − = 波形信道被简化成一个等效的离散时间信道! 处理 —— 矢量AWGN信道模型: 信道模型和信道容量 ⚫输入是波形 ⚫输出也是波形 0 [ ( ) ( )] ( ) T i i i = + = + x t n t t dt x n 其中: 由于{ni }不相关,高斯分布 为了定义一组能体现信道特性的概率:

信道模型和信道容量 由维度定理:带宽为W、时长为T的信号空间维数:N=2WT T/2 考虑到信道输入通常受功率限制: lim x2(t)di≤p T→0T -T/2 2WT 即 -T/2 正交性 =lim元2wTE[X2]=2wE[X2]sP→ T→0T E[x']s 大数定 结论: 波形AWGN信道 等效的离散时间AWGN信道 带宽W限制; 等效于 每秒使用2W次; 功率P限制 噪声方差:σ2=NJ2 输入功率受限于: |r]品 10
10 带宽为W、时长为T的信号空间维数:N=2WT / 2 2 / 2 1 lim ( ) → − T T T x t dt P T 2 2 P E X W 由维度定理: 考虑到信道输入通常受功率限制: 信道模型和信道容量 即: 结论: 波形AWGN信道 带宽W限制; 功率P限制 等效的离散时间AWGN信道 每秒使用2W次; 噪声方差:2=N0 /2 输入功率受限于: 2 2 P E X W 等效于 / 2 2 2 2 / 2 1 1 1 lim ( ) lim T WT j T T T j x t dt x → → T T − = = 1 2 2 lim 2 2 T WTE X WE X P → T = = 正交性 大数定理