
Chapter 4 AWGN信道的最佳接收机 ●信号经发送端调制后进入信道,在信道中要受到噪声干扰和各种 信道损伤,最后被接收机接收。 ●研究噪声对第3章的调制系统可靠性的影响 ●研究AWGN信道最佳接收机的设计和性能特征
Chapter 4 AWGN信道的最佳接收机 ⚫研究噪声对第3章的调制系统可靠性的影响 ⚫研究AWGN信道最佳接收机的设计和性能特征 ⚫信号经发送端调制后进入信道,在信道中要受到噪声干扰和各种 信道损伤,最后被接收机接收

4.2波形与矢量AWGN信道 ●信道的特征决定了信号受到那些损伤,决定了信道性能中的关键 因素。 ●先从最简单的AWDN信道着手。 2
2 4.2 波形与矢量AWGN信道 ⚫信道的特征决定了信号受到那些损伤,决定了信道性能中的关键 因素。 ⚫先从最简单的AWDN信道着手

波形与矢量AWGN信道 波形与矢量AWGN信道 s(t) r(t) m r(t)=s,(t)+n(t) n(t) 任务: 将这样一个波形信道模型用一个失量模型来表示!
波形与矢量AWGN信道 sm(t) n( t ) r( t )=sm(t) + n(t) 波形与矢量 r( t ) AWGN信道 m m ˆ 将这样一个波形信道模型用一个矢量模型来表示! 任务:
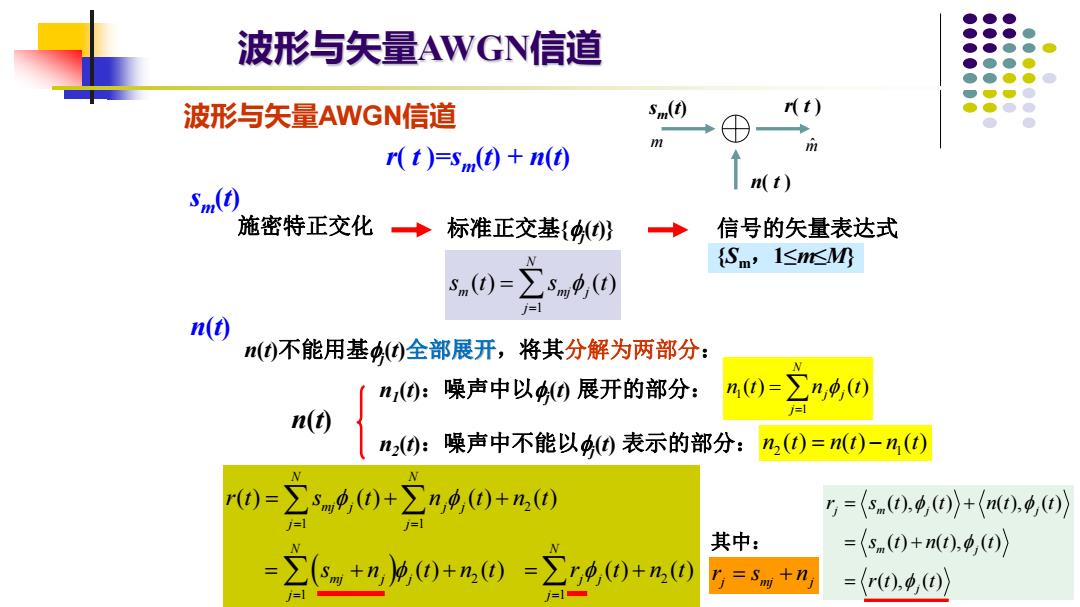
波形与矢量AWGN信道 波形与矢量AWGN信道 sm(t) r(t) m r(t)=Sm()+n() (t) Sm(t) 施密特正交化◆ 标准正交基{} 信号的矢量表达式 {Sm,1≤KM0 50=∑,0 i= n() ()不能用基(①全部展开,将其分解为两部分: n():噪声中以0展开的部分: m0=∑n@ n() n2①):噪声中不能以0表示的部分:n()=n(t)-n() r0=∑s,0+∑n,,0+n) =(sn(),()》+(0),(0〉 其中 =〈sn())+n),,()》 =∑(s,+0+%0=立0+%0 =Smi +n =〈r(0,9(@》
波形与矢量AWGN信道 sm(t) n( t ) r( t )=sm(t) + n(t) 波形与矢量 r( t ) AWGN信道 施密特正交化 标准正交基{j (t)} 信号的矢量表达式 {Sm,1≤m≤M} n(t)不能用基j (t)全部展开,将其分解为两部分: 1 ( ) ( ) N m mj j j s t s t = = n1 (t):噪声中以j (t) 展开的部分: n2 (t):噪声中不能以j (t) 表示的部分: n(t) n(t) sm(t) 1 1 ( ) ( ) N j j j n t n t = = 2 1 n t n t n t ( ) ( ) ( ) = − ( ) 2 1 1 2 2 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) N N mj j j j j j N N mj j j j j j j r t s t n t n t s n t n t r t n t = = = = = + + = + + = + j mj j r s n = + 其中: m m ˆ ( ), ( ) ( ), ( ) ( ) ( ), ( ) ( ), ( ) = + = + = j m j j m j j r s t t n t t s t n t t r t t

波形与矢量AWGN信道 r0=∑j40+n,0) 其中: r=Sm +n 思考 1.n是否还具有与n()完全一样的性质? 2.2()的舍弃,会不会丢弃了某些有用的信息, 影响最终判决?
波形与矢量AWGN信道 2 1 ( ) ( ) ( ) N j j j r t r t n t = = + j mj j 其中: r s n = + 1. nj是否还具有与n(t)完全一样的性质? 2. n2 (t)的舍弃,会不会丢弃了某些有用的信息, 影响最终判决? 思考
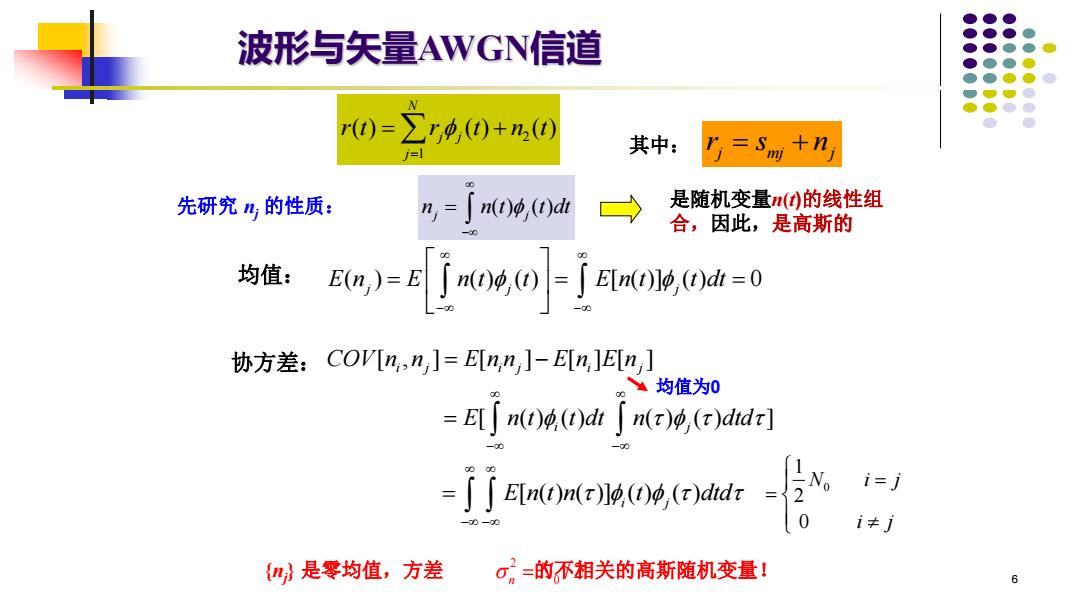
波形与矢量AWGN信道 r0=∑y4(0+n,(0 其中: =Smi+n 先研究n,的性质: 是随机变量()的线性组 合,因此,是高斯的 均值:u)=Ea0o0-了m00d=0 协方差:COV[n,n]=E[n,n]-ELn,]ELn,] 均值为0 =Ejmo)40d∫mr4(r)dd -EIn(((dd i=j 0 i≠j {n}是零均值,方差 σ=的不相关的高斯随机变量! 6
6 波形与矢量AWGN信道 ( ) ( ) ( ) [ ( )] ( ) 0 E n E n t t E n t t dt j j j − − = = = 0 1 2 0 N i j i j = = [ , ] [ ] [ ] [ ] [ ( ) ( ) ( ) ( ) ] i j i j i j i j COV n n E n n E n E n E n t t dt n dtd − − = − = 均值: 协方差: {nj } 是零均值,方差 2 的不相关的高斯随机变量! 0 / 2 n = N 先研究 nj 的性质: 2 1 ( ) ( ) ( ) N j j j r t r t n t = = + j mj j r s n = + ( ) ( ) j j n n t t dt − = 其中: 是随机变量n(t)的线性组 合,因此,是高斯的 [ ( ) ( )] ( ) ( ) E n t n t dtd i j − − = 均值为0

波形与矢量AWGN信道 再研究2的性质: n2(t)=nt)-n(0) 40=之40 (t)=n(t)-n,(t) = ◆n,是联合高斯随机变量n1是高斯过程n,是也是高斯过程; ◆n2(0与{r}是不相关的。 考察: E[n,()r],=[n,sm+E[n,()n,】=En,()n,] 均值为0 r=Sw+n =n-立oj小 40=n0)-立nAe i=1 n,=n()o()dr ∫E[n)n(r),(r)dr-∑E[nn,l4() -1N,j6l-rM,(r)dr-N.4,(0) =号Np,0-)N9,0=0 7
7 2 2 [ ( )] [ ( ) ] = + E n t s E n t n mj j 波形与矢量AWGN信道 再研究 n2 的性质: 2 1 n t n t n t ( ) ( ) ( ) = − ◆nj是联合高斯随机变量 → n1 (t)是高斯过程 → n2 (t)是也是高斯过程; ◆n2 (t)与{rj }是不相关的。 1 1 ( ) ( ) N j j j n t n t = = 2 1 n t n t n t ( ) ( ) ( ) = − 考察: 1 ( ) ( ) N i i j i E n t n t n = = − 0 0 0 0 1 1 ( ) ( ) ( ) 2 2 1 1 ( ) ( ) 0 2 2 j j j j N t d N t N t N t − = − − = − = 2 [ ( ) ] E n t rj 0 1 [ ( ) ( )] ( ) [ ] ( ) T N j i j i i E n t n d E n n t = = − 2 [ ( ) ] = E n t nj j mj j r s n = + 0 ( ) ( ) T j j n n d = 均值为0 2 1 ( ) ( ) ( ) N i i i n t n t n t = = −

加性高斯白噪声信道的最佳接收机 结论: n2(0独立于{r。 因为{r}是携带发送信号的唯一分量,所以,,(0不包含与 发送信号有关的任何信息,即,()对信号的最终检测是无关 的信息。可以忽略而不影响检测器的最佳性。 AWGN波形信道 等效于 N维矢量信道 r(t)=s,(t)+n(t) =Sm+n 8
8 结论: n2 (t) 独立于{rj }。 因为{rj } 是携带发送信号的唯一分量,所以, n2 (t)不包含与 发送信号有关的任何信息,即n2 (t)对信号的最终检测是无关 的信息。可以忽略而不影响检测器的最佳性。 加性高斯白噪声信道的最佳接收机 AWGN波形信道 N维矢量信道 m r t s t n t ( ) ( ) ( ) = + m r s n = + 等效于

4.2.2 ,AWGN信道的最佳接收机 ●讨论在发送信号受到加性高斯噪声影响下,各种调制方法的 最佳接收机如何设计?性能如何?
9 4.2.2 AWGN信道的最佳接收机 ⚫讨论在发送信号受到加性高斯噪声影响下,各种调制方法的 最佳接收机如何设计?性能如何?
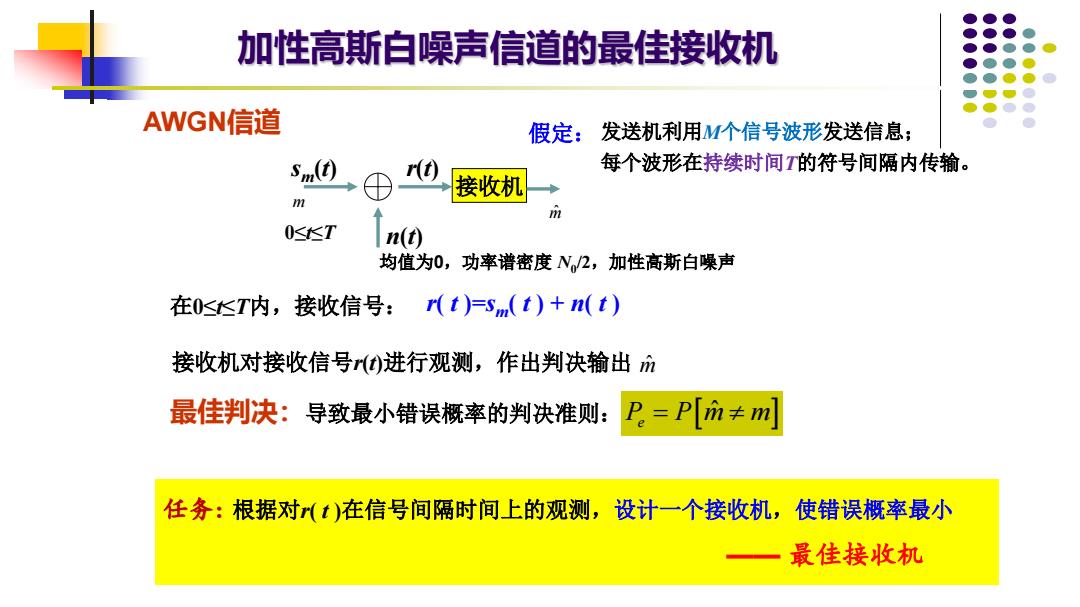
加性高斯白噪声信道的最佳接收机 AWGN信道 假定:发送机利用M个信号波形发送信息; Sm(t) (t) 每个波形在持续时间的符号间隔内传输。 接收机 m (<KT n(t) 均值为0,功率谱密度N2,加性高斯白噪声 在0<T内,接收信号:r(t)=Sm(t)+n(t) 接收机对接收信号)进行观测,作出判决输出m 最佳判决:导致最小错误概率的判决准则: P=P[m≠m] 任务:根据对(t)在信号间隔时间上的观测,设计一个接收机,使错误概率最小 最佳接收机
加性高斯白噪声信道的最佳接收机 任务: 根据对r( t )在信号间隔时间上的观测,设计一个接收机,使错误概率最小 —— 最佳接收机 sm(t) n(t) r( t )=sm( t ) + n( t ) r(t) 接收机 m ˆ m AWGN信道 发送机利用M个信号波形发送信息; 每个波形在持续时间T的符号间隔内传输。 最佳判决:导致最小错误概率的判决准则: P P m m e = ˆ 0≤t≤T 假定: 在0≤t≤T内,接收信号: 均值为0,功率谱密度 N0 /2,加性高斯白噪声 接收机对接收信号r(t)进行观测,作出判决输出 m ˆ