
第2章确定与随机信号分析 ·介绍后续各章所需的背景知识 ●自己复习相关的基础知识:傅里叶变换及 其性质;随机过程,等等
第2章 确定与随机信号分析 ⚫介绍后续各章所需的背景知识 ⚫自己复习相关的基础知识:傅里叶变换及 其性质;随机过程,等等

2.1带通与低通信号的表示 带通信号 (系统) 是一种实窄带高频信号,其频谱集中在某个频率(土)附近, 且频谱宽度远小于∫的信号(系统) ◆双边带调制DSB: 传输信号的信道带宽限制在以载 波为中心的一个频段上。 (a)Magnicode Spectrum of Modulation Discrete carrier term hgb=二A ◆单边带调制SSB: 传输信号的信道带宽限制在邻近 载波的频段上。 (b)Magnitude Spectnim of AM Signa Figure 4-2 Spectrum of AM signal 本节目的: 希望将所有带通信号与系统简化为等效低通信号,这样可以 大大简化带通信号的处理。 2
2 2.1 带通与低通信号的表示 带通信号(系统) ◆双边带调制DSB: 传输信号的信道带宽限制在以载 波为中心的一个频段上。 ◆单边带调制SSB: 传输信号的信道带宽限制在邻近 载波的频段上。 本节目的: 希望将所有带通信号与系统简化为等效低通信号,这样可以 大大简化带通信号的处理。 是一种实窄带高频信号,其频谱集中在某个频率(±f0)附近, 且频谱宽度远小于f0的信号(系统)

2.1带通与低通信号的表示 理论依据: 实信号x()的傅里叶变换特性: (Hermitian对称性) X(-f)=X(f) 幅度偶对称 X(-f)=X'(f) X(f)=-∠X(f) 相位奇对称 结论: x(0的全部信息都包含在正(或负)频域中,由X(f)(f>0)可以 完整地重构x() 事实上: X(f)=X(f)+X_(f) =X(f)+X(-f) 表明X(f)对重构X(f)是充分的! x()的带宽定义为最小的正频率范围,当|f引超出该范围时,X(f)=0
3 2.1 带通与低通信号的表示 理论依据: 实信号x(t)的傅里叶变换特性: * X f X f ( ) ( ) − = X f X f ( ) ( ) − = * = − X f X f ( ) ( ) 结论: x(t)的全部信息都包含在正(或负)频域中,由X( f )(f >0)可以 完整地重构 x(t) 事实上: * ( ) ( ) ( ) ( ) ( ) X f X f X f X f X f + − + + = + = + − 表明X+ ( f )对重构X( f ) 是充分的! 幅度偶对称 相位奇对称 (Hermitian对称性) x(t)的带宽定义为最小的正频率范围,当| f |超出该范围时,X( f )=0

2.1带通与低通信号的表示 定义 x()的解析信号一x()傅里叶变换中正频率的部分X(f) 设带通信号x(t)频谱:X(f) 1X01 则: x.(f)=x(Au(f U(f):单位阶跃函数 fo fo 时域表达式: x(t)=F-[x(f)] =F-[X(f)]*F-[w(f)】 =0[380+j2)0+0】 0=0: 等价于一个滤波器在x()激励下的输出。 4
4 定义 x(t)的解析信号 ——x(t)傅里叶变换中正频率的部分X+ ( f ) 设带通信号x( t )频谱:X( f ) 时域表达式: 1 X f X f u f ( ) ( ) ( ) + − = 1 ( ) ( ) ˆ 2 = + x t jx t 1 1 1 F X f F u f [ ( )] [ ( )] − − = − 1 x t F x f ( ) [ ( )] − + + = 1 1 ( ) ( ) 2 2 x t t j t = + U-1 ( f ):单位阶跃函数 1 1 ( ) ˆ( ) ( ) x x t x t d t t − = = − 等价于一个滤波器在x(t)激励下的输出。 2.1 带通与低通信号的表示 则: f0 -f0 | X(f) |
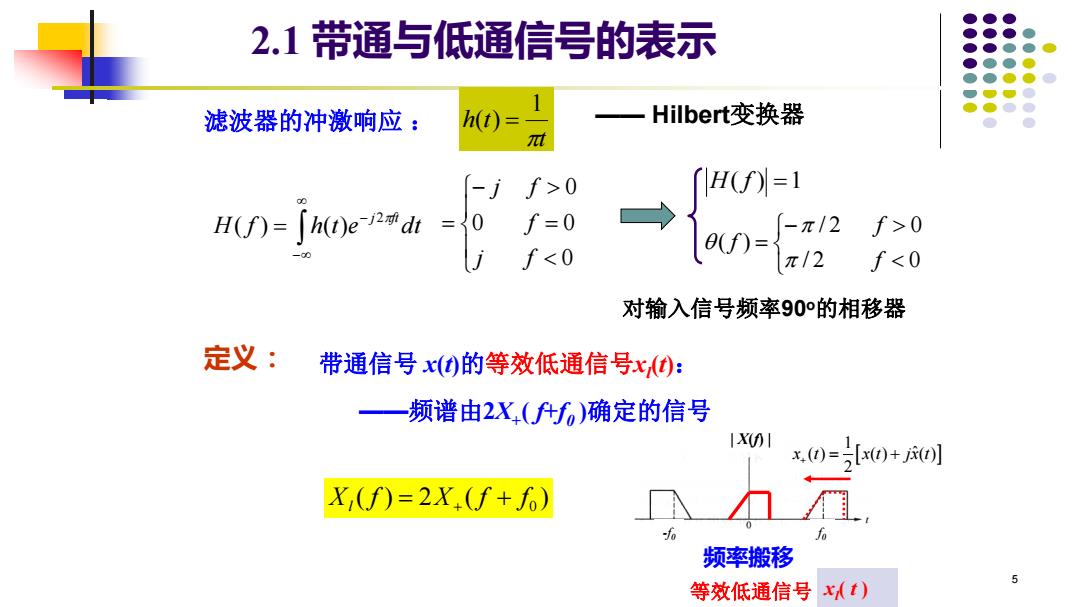
2.1带通与低通信号的表示 滤波器的冲激响应: h(t)= 一Hilbert变换器 -jf>0 H(f=1 f=0 a-2 f>0 f<0 π/2 f<0 对输入信号频率90°的相移器 定义:带通信号x()的等效低通信号x: 频谱由2X(什f)确定的信号 IXI x()=[x)+)] X(f)=2X(f+f0) 频率搬移 5 等效低通信号()
5 对输入信号频率90o的相移器 滤波器的冲激响应 : − − H f = h t e dt j2ft ( ) ( ) − = / 2 0 / 2 0 ( ) f f f H( f ) =1 = − = 0 0 0 0 j f f j f t h t 1 ( ) = —— Hilbert变换器 2.1 带通与低通信号的表示 定义 : 带通信号 x(t)的等效低通信号xl (t): 0 ( ) 2 ( ) X f X f f l = + + ——频谱由2X+ ( f+f0 )确定的信号 频率搬移 f0 -f0 | X(f) | 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + xl 等效低通信号 ( t )

2.1带通与低通信号的表示 归纳3个名词的含义及关系 带通信号: x(f) 解析信号: X.(f)=x(Au(f) x,0=0+ x)=[x0+)】 等效低通信号:X,(f)=2X(f+f)
2.1 带通与低通信号的表示 0 ( ) 2 ( ) X f X f f l = + + f0 -f0 | X(f) | 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + 归纳 3个名词的含义及关系 带通信号: 解析信号: 等效低通信号: X f ( ) 1 X f X f u f ( ) ( ) ( ) + − = f0 -f0 | X+ (f) | f0 | X (f) | 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + -f0

2.1带通与低通信号的表示 X,(f)=2X,(f+f0) 时域: x()=F-[X,(f)] x0=,[x0+)] =2x(t)e-j2xh =三[x(0+u)]e2x =[x(t)cos2πft+x(t)sin2πft]+ +j(t)cos2πjft-x(t)sin2πft] x(t)=Refx,(t)e2 等效低通表达式 任何一个带通信号 都可以用其等效低 xU)=[x,-)+X-f-] 通信号来表示! x以t)一般是复低通信号: x,(t)=x,(t)+jx,(t) 同相分量 正交分量 7
7 0 1 2 ( ) ( ) 2 ( ) − − + = = l l j f t x t F X f x t e 时域: ( ) ( ) ( ) l i q xl ( t )一般是复低通信号: x t x t jx t = + 0 0 0 0 [ ( )cos 2 ( )sin 2 ] ˆ [ ( )cos 2 ( )sin 2 ] ˆ x t f t x t f t j x t f t x t f t = + + + − 2.1 带通与低通信号的表示 0 ( ) 2 ( ) X f X f f l = + + 任何一个带通信号 都可以用其等效低 通信号来表示! * 0 0 1 ( ) ( ) ( ) 2 X f X f f X f f l l = − + − − 0 2 ( ) Re ( ) j f t l x t x t e = 同相分量 正交分量 等效低通表达式 1 ( ) ( ) ( ) ˆ 2 x t x t jx t + = + 0 2 ( ) ( ) ˆ − = + j f t x t jx t e

2.1带通与低通信号的表示 x(t)=x,()+jx,(t) x,(t)=[x(t)cos2πfot+x(t)sin2πf] x,(t)=[(t)cos2πf6t-x(t)sin2πft] 任何一个带通信号都可 x(t)=x,(t)cos2πft-x,(t)sin2πft 以用两个低通信号来表 示!(同相分量,正交 正交表达式 分量) 极坐标形式 由:x,)=x,(0+jx,() x,(t)=r(te8四 其中: r()=Vx()+x0 代入x0=Re{5)e2e,o} 80)=tan,@ x,(t) x(t)=r(t)cos[2zft+e(t)] 极坐标表达式 8
8 ( ) ( ) ( ) l i q 由: x t x t jx t = + 0 0 ( ) [ ( )cos 2 ( )sin 2 ] ˆ q x t x t f t x t f t = − 2.1 带通与低通信号的表示 任何一个带通信号都可 以用两个低通信号来表 示!(同相分量,正交 分量) 极坐标形式 ( ) ( ) ( ) l i q x t x t jx t = + 0 0 ( ) [ ( ) cos 2 ( )sin 2 ] ˆ i x t x t f t x t f t = + 0 0 ( ) ( )cos 2 ( )sin 2 i q x t x t f t x t f t = − ( ) ( ) ( ) x j t l x x t r t e = 1 ( ) ( ) tan ( ) q i x t t x t − = 2 2 ( ) ( ) ( ) x i q r t x t x t = + 0 ( ) ( ) cos[2 ( )] x x x t r t f t t = + 其中: 代入 0 2 ( ) ( ) Re ( ) x j f t t x x t r t e + = 极坐标表达式 正交表达式
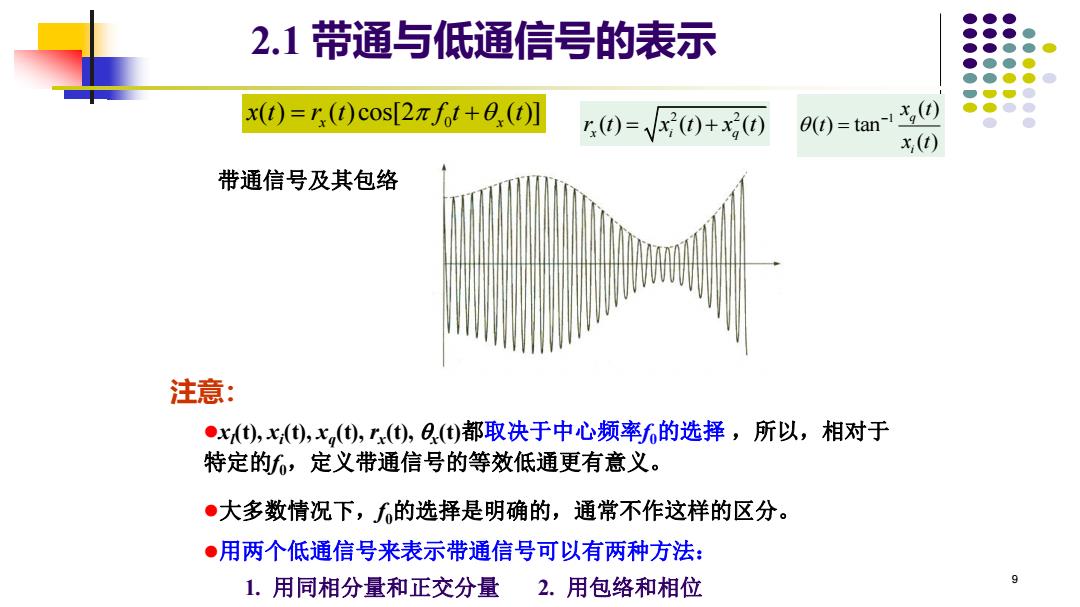
2.1带通与低通信号的表示 x(t)=r,(t)cos[2ft+e(t)] r0=√(0+x回 80=tan1@ x,(t) 带通信号及其包络 注意: ●x),x(),x,(),r(),()都取决于中心频率的选择,所以,相对于 特定的f,定义带通信号的等效低通更有意义。 ●大多数情况下,f的选择是明确的,通常不作这样的区分。 ●用两个低通信号来表示带通信号可以有两种方法: 1.用同相分量和正交分量2.用包络和相位 9
9 1 ( ) ( ) tan ( ) q i x t t x t − = 2 2 ( ) ( ) ( ) x i q 0 r t x t x t = + ( ) ( ) cos[2 ( )] x x x t r t f t t = + 2.1 带通与低通信号的表示 注意: ⚫xl (t), xi (t), xq (t), rx (t), x (t)都取决于中心频率f0的选择 ,所以,相对于 特定的f0,定义带通信号的等效低通更有意义。 ⚫大多数情况下,f0的选择是明确的,通常不作这样的区分。 带通信号及其包络 ⚫用两个低通信号来表示带通信号可以有两种方法: 1. 用同相分量和正交分量 2. 用包络和相位

2.1带通与低通信号的表示 归纳 带通信号的3种表达式(含义,关系,应用) 等效低通表达式: x(t)=Re{x(t)e 分析,计算频谱,功率,带宽. 正交表达式: x(t)=x,(t)cos2nft-x (t)sin2fot 实现,可两路,也可仅一路 极坐标表达式: x(t)=r(t)cos[2zfot+e(t] 直观理解,传输信息承载在高 频信号的包络和相位上
0 ( ) ( ) cos[2 ( )] x x x t r t f t t = + 2.1 带通与低通信号的表示 归纳 带通信号的3种表达式 (含义,关系,应用) 等效低通表达式: 正交表达式: 极坐标表达式: 0 2 ( ) Re ( ) j f t l x t x t e = 0 0 ( ) ( )cos 2 ( )sin 2 i q x t x t f t x t f t = − 分析,计算频谱,功率,带宽… 实现,可两路,也可仅一路 直观理解,传输信息承载在高 频信号的包络和相位上