
5.2.5 ,非面向判决环 1
1 5.2.5 非面向判决环

下面研究信号s(,)携带信息序列{I}时的相位估计 问题:在求A()时: AMo)=Cexpl-∫r0su,pai 0 T A,0=是」r0u,a o T 如何处理信息序列{L}? 两种方法: ●将{I}作为已知项来处理。一面向判决环 假定观测区间上信息序列已估计出来,并且不存在解调差错为=1; 即:△(倒中,即除了中 以外,s(6是确知的 ●将{I}作为随机序列,并在其统计上求平均一非面向判决环
下面研究信号s(t, ) 携带信息序列 { In }时的相位估计 ⚫将 { In } 作为已知项来处理。—— 面向判决环 两种方法: ⚫将 { In } 作为随机序列,并在其统计上求平均 —— 非面向判决环 问题: ( ) ( , ) ] 2 ( ) exp[ 0 0 r t s t dt N C T = r t s t dt N T L = 0 ( ) ( , ) 2 ( ) 0 如何处理信息序列 {In } ? 在求 ( ) 时: 假定观测区间上信息序列已估计出来,并且不存在解调差错 I I % n n = ; 即:L ()中,即除了 以外,s(t, ) 是确知的

非面向判决环 5.2.5非面向判决环 思想:将数据序列{I}处理为随机变量,并在最大化前将△(对 这些随机变量求平均。 求平均需要用到数据的概率分布,如何得到? ●当已知数据的实际概率分布时,直接利用它; ●当不知道数据的实际概率分布时,可以作合理的近似。 例1:二进制已调信号: s(t)=Acos2πf61 0≤t≤T (在一个信号间隔内) A=±1且等概,A的PDF: P(4=26(4-)+26(4+1) (倒-0 x=0 others 3
3 ( ) 2 0 c s t Acos f t t T = ( ) ( ) ( ) ( ) 1 1 1 0 1 1 2 2 0 x P A A A x others = = − + + = 5.2.5 非面向判决环 思想:将数据序列{ In }处理为随机变量,并在最大化前将 () 对 这些随机变量求平均。 例1:二进制已调信号: A=±1且等概,A的PDF: 求平均需要用到数据的概率分布,如何得到? ⚫当已知数据的实际概率分布时,直接利用它; ⚫当不知道数据的实际概率分布时,可以作合理的近似。 非面向判决环 (在一个信号间隔内)

非面向判决环 将似然函数人(中)在A的这两个值上求平均: )=」(P(4d-ien是r0cos(ex+jh ex+e x coshx= +2n是r0os(2rfr+)h 2 =cosh 是r0)cos2rfn+)h 对数似然函数:人z(=Incosh 天jr02x+a 令 dΛ(p) ≥0 ·非面向判决的ML估计 d中 x 当互相关比较小时, 为了简化,可以采用近似: In coshx≈ 对数似然函数包含有 x x>1 一个平方项。 4 般情况下,可假定符号是零均值高斯变量,然后再求平均似然函数
4 cosh 2 x x e e x − + = 将似然函数 ( ) 在A的这两个值上求平均: ( ) ( ) 0 0 2 cosh 2 = + T c r t cos f t dt N ( ) ( ) ( ) ( ) 0 0 0 0 1 2 exp 2 2 1 2 exp 2 2 = + + − + T c T c r t cos f t dt N r t cos f t dt N ( ) ( )P A dA ( ) − = 对数似然函数: 0 0 2 ( ) lncosh ( )cos(2 ) T L c r t f t dt N = + 0 ( ) = d d L 令 非面向判决的ML估计 为了简化,可以采用近似: 1 2 | | 1 ln cosh 2 | | | | 1 x x x x x 一般情况下,可假定符号是零均值高斯变量,然后再求平均似然函数 非面向判决环 当互相关比较小时, 对数似然函数包含有 一个平方项

非面向判决环 例2:在上例中,假设信号幅度八是零均值高斯随机变量,具有单位方差, P(A)= e √2π 在A的PDF上对A(求平均,可得平均似然函数: )=Cexp [&irnae+5a 相应的对数似然函数: 令 dAi() 0 即可得中的ML估计值 说明: d中 In coshx= 2 |xk<1 ●在高斯假设情况下,对数似然函数具有平方项; 2 ●在前面例子中,当(①与s(,)的互相关值比较小时,也是近似平方的; ●所以,如果互相关值比较小,对信息符号的分布作高斯假设就可以得到 对数似然函数较好的近似。 5
5 例2: 在上例中,假设信号幅度A是零均值高斯随机变量,具有单位方差, / 2 2 2 1 ( ) A P A e − = = + 2 0 0 ( ) cos(2 ) 2 ( ) exp T c r t f t dt N C 2 0 0 ( ) cos(2 ) 2 ( ) = + T c L r t f t dt N 在A的PDF上对Λ() 求平均,可得平均似然函数: 相应的对数似然函数: 0 ( ) = d d L 令 即可得 的ML估计值 ⚫在高斯假设情况下,对数似然函数具有平方项; ⚫在前面例子中,当r(t)与s(t,)的互相关值比较小时,也是近似平方的; ⚫所以,如果互相关值比较小,对信息符号的分布作高斯假设就可以得到 对数似然函数较好的近似。 说明: 非面向判决环 1 2 ln cosh | | 1 2 x x x =
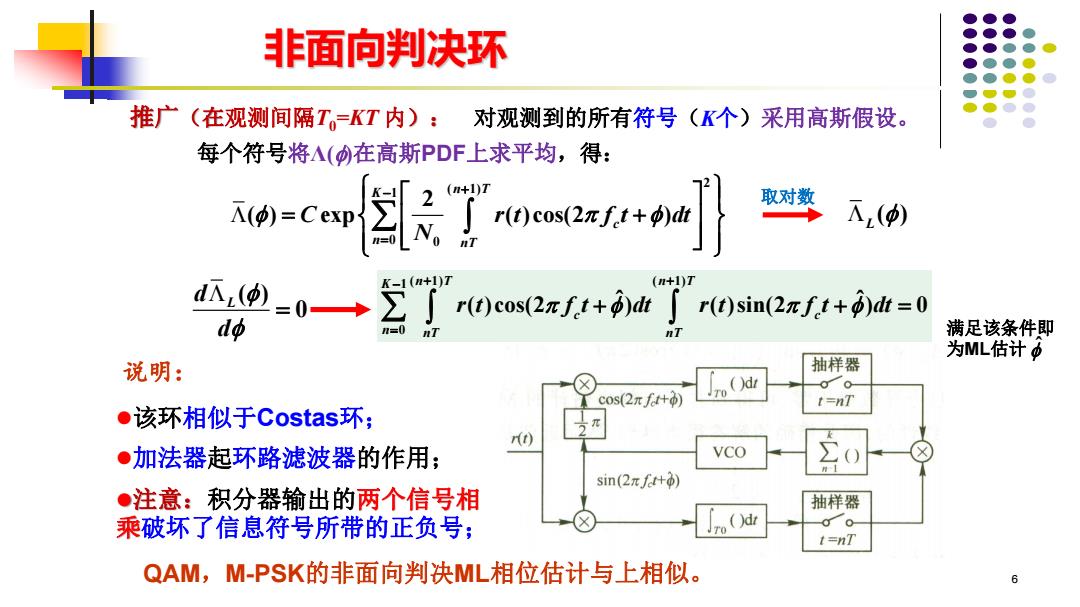
非面向判决环 推广(在观测间隔T。=KT内):对观测到的所有符号(K个)采用高斯假设。 每个符号将A()在高斯PDF上求平均,得: (n+1)7 取对数 人(φ) 4,@-0→了r0co2mf+hJ k-1(+1)7 +1)7 r(t)sin(2πft+p)dt=0 dφ 满足该条件即 为ML估计P 说明: 抽样器 ()d 00 cos(2πf+p) t=nT ●该环相似于Costas环; rt) ●加法器起环路滤波器的作用; sin(2πf+) ·注意:积分器输出的两个信号相 抽样器 乘破坏了信息符号所带的正负号; ()d t=nT QAM,M-PSK的非面向判决ML相位估计与上相似。 6
ˆ 满足该条件即 为ML估计 6 推广(在观测间隔T0=KT 内): 2 ( 1) 1 0 0 2 ( ) exp ( )cos(2 ) K n T c n nT C r t f t dt N + − = = + ⚫该环相似于Costas环; ⚫加法器起环路滤波器的作用; ⚫注意:积分器输出的两个信号相 乘破坏了信息符号所带的正负号; ( ) 0 L d d = ( 1) ( 1) 1 0 ˆ ˆ ( )cos(2 ) ( )sin(2 ) 0 K n T n T c c n nT nT r t f t dt r t f t dt + + − = + + = 说明: QAM,M-PSK的非面向判决ML相位估计与上相似。 每个符号将Λ()在高斯PDF上求平均,得: 对观测到的所有符号(K个)采用高斯假设。 非面向判决环 ( ) L 取对数
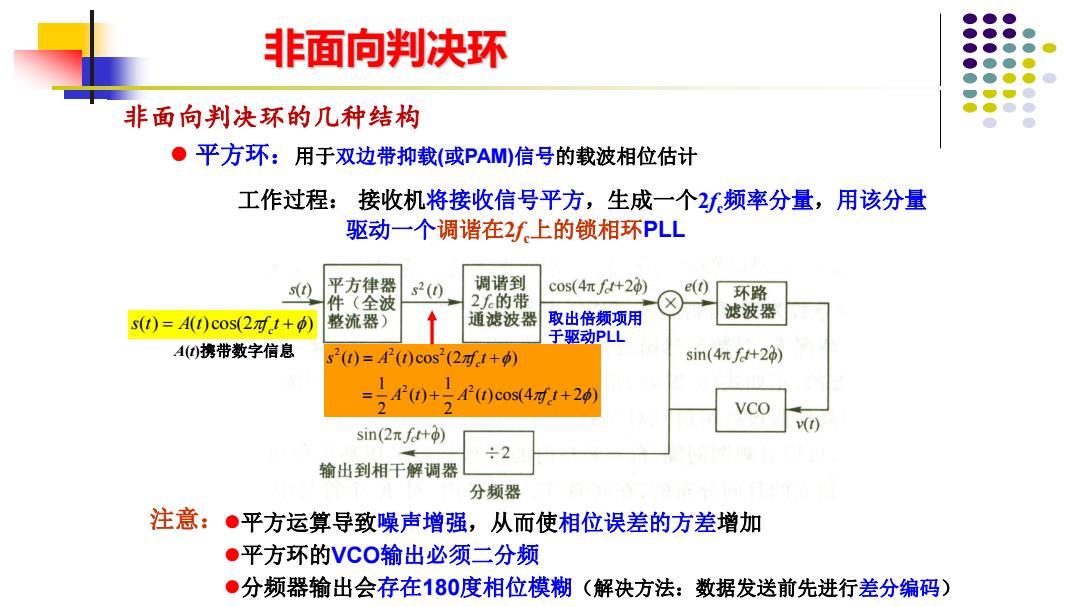
非面向判决环 非面向判决环的几种结构 ●平方环:用于双边带抑载(或PAM信号的载波相位估计 工作过程: 接收机将接收信号平方,生成一个2f频率分量,用该分量 驱动一个调谐在2f上的锁相环PLL 平方律器 s2(0 调谐到 cos(4πf+20 e(t) 件(全波 2f6的带 环路 s(1)=A(1)c0s(2可1+) 整流器) 通滤波器 取出倍频项用 滤波器 于驱动PLL A()携带数字信息 s2(t)=A2(t)cos(21+φ) sin(4nft+20) =4r0+40cos41+2 sin(2πf+) ÷2 输出到相干解调器 分频器 注意:●平方运算导致噪声增强,从而使相位误差的方差增加 ●平方环的VCO输出必须二分频 ●分频器输出会存在180度相位模糊(解决方法:数据发送前先进行差分编码)
7 非面向判决环的几种结构 ⚫ 平方环:用于双边带抑载(或PAM)信号的载波相位估计 接收机将接收信号平方,生成一个2fc频率分量,用该分量 驱动一个调谐在2fc上的锁相环PLL s(t) = A(t) cos(2f t +) c ( ) cos(4 2 ) 2 1 ( ) 2 1 ( ) ( ) cos (2 ) 2 2 2 2 2 = + + = + A t A t f t s t A t f t c c ⚫平方运算导致噪声增强,从而使相位误差的方差增加 ⚫平方环的VCO输出必须二分频 ⚫分频器输出会存在180度相位模糊(解决方法:数据发送前先进行差分编码) 注意: 取出倍频项用 于驱动PLL 非面向判决环 工作过程: A(t)携带数字信息
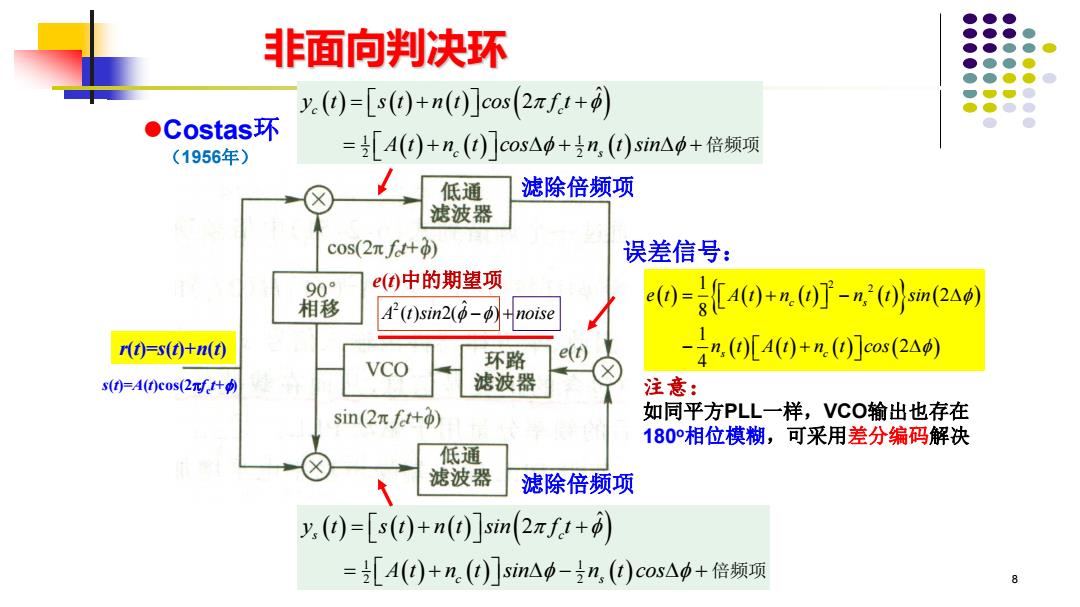
非面向判决环 y.())=[s(0)+n()]cos2πft+p) ●Costas环 (1956年) =[A()+n.()]cos△p+号n,()sin△+倍频项 低通 滤除倍频项 滤波器 cos(2πf+) 误差信号: 90° e()中的期望项 相移 A2(0sin2(p-p) e)=8A)+(O]-m,2)sn(2△) noise t)=s(t0)+(t) 环路 e(t) -4n,(O)[AO+n.()]cos(2△) VCo s0=A(0c0s(2f什 滤波器 注意: sin(2πfe+p) 如同平方PLL一样,VCO输出也存在 180°相位模糊,可采用差分编码解决 低通 滤波器 滤除倍频项 y,()=[s(@+n()]sin(2πf+) =[A()+n.()]simA-n,()cos△0+倍频项 8
双边带PAM信号载波相位估计的另一种方案 8 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 2 ˆ 2 s c c s y t s t n t sin f t A t n t sin n t cos = + + = + − + 倍频项 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 2 2 8 1 2 4 = + − − + c s s c e t A t n t n t sin n t A t n t cos ⚫Costas环 误差信号: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 2 ˆ 2 c c c s y t s t n t cos f t A t n t cos n t sin = + + = + + + 倍频项 滤除倍频项 2 ˆ A t sin noise ( ) 2( ) − + r(t)=s(t)+n(t) 滤除倍频项 注意: 如同平方PLL一样,VCO输出也存在 180o相位模糊,可采用差分编码解决 非面向判决环 e(t)中的期望项 s(t)=A(t)cos(2fc t+) (1956年)

非面向判决环 多相位信号的载波估计M-PSK M相信号:s(t)=Acos 2πft+中+ 2z(m-0 m=1,2,.M ◆方法一:平方环推广 载波相位中携带的信息分量 载波恢复的实质:去除信息分量,从而 ◆方法二:基于Costas环的推广 得到未调载波 cos(2πMf1+M) 平方环推广◆方律器件 接收信号 M方 调诸到 MfE的带 环路 ●带通滤波器选择谐波 s(t) 律器件 滤波器 通滤波器 sin(2 rMft-+M⊙) cos(2πMf.t+Mφ) ●将接收信号进 行M次方运算 VCO 来驱动PLL,由于M次谐波中: M2zm-1)=2πm-1)=0 分频器 M ÷M 因此,信息被除去; 输出 ●VCO输出: sin(2πMf.t+M) ●VCO的输出被M分频 后,产生sin(2付t+φ) 9
平方环推广 M方律器件 9 ● 带通滤波器选择谐波 来驱动PLL,由于M次谐波中: 多相位信号的载波估计 M-PSK M相信号: 2 ( ) cos 2 ( 1) c s t A f t m M = + + − cos(2 ) Mf t M c + m = 1, 2, … M ) ˆ sin(2Mfc t + M 因此,信息被除去; 2 M m m ( 1) 2 ( 1) 0 M − = − = ◆方法一:平方环推广 ◆方法二:基于Costas环的推广 ⚫VCO的输出被M分频 后,产生 非面向判决环 sin(2f t +) c 载波相位中携带的信息分量 ⚫将接收信号进 行M次方运算 ● VCO输出: ) ˆ sin(2Mfc t + M 载波恢复的实质:去除信息分量,从而 得到未调载波 cos(2 ) Mf t M c + st( )

非面向判决环 多相位信号的载波估计M-PSK 方法二:基于Costas环的推广 (实现较为复杂,实际中一般不采用)
方法二:基于Costas环的推广 非面向判决环 (实现较为复杂,实际中一般不采用) 多相位信号的载波估计 M-PSK