
4.3 带限信号传输的最佳检测 和错误概率 信号类型:ASK,PSK,QAM 主要特征:低带宽需求,传输方式具有低维度,且与发 送信号的数目无关,功率效率随消息数的增加而减小。 1
1 4.3 带限信号传输的最佳检测 和错误概率 信号类型:ASK,PSK,QAM 主要特征:低带宽需求,传输方式具有低维度,且与发 送信号的数目无关,功率效率随消息数的增加而减小

4.3.1ASK或PAM信号 传输的最佳检测和错误概率 2
2 4.3.1 ASK或PAM信号 传输的最佳检测和错误概率

带限信号传输的最佳检测和错误概率 ASK信号(M个一维信号点) 两相邻信号点 之间的距离: m+】 m=1,2,..,M nin Am=(2m-1-M0 12l0g2 M 任意相邻两点之间的最小距离: dmin M2-1 E bavg 最大相关度量判决规则 选择离最近的幅度电平为判决输出 思考 如果发生差错?会在哪些情形下出现差错? 差错概率怎样计算?
选择离r最近的幅度电平为判决输出 带限信号传输的最佳检测和错误概率 ASK信号(M个一维信号点) m g Am s 2 1 = 任意相邻两点之间的最小距离: m =1, 2, …,M (2 1 ) A m M m = − − 2 min 2 12log 1 bavg M d M = − 最大相关度量判决规则 sm sm+1 sm-1 两相邻信号点 之间的距离: min d 如果发生差错?会在哪些情形下出现差错? 差错概率怎样计算? 思考

带限信号传输的最佳检测和错误概率 ASK信号(M个一维信号点) 两相邻信号点 之间的距离: -】 Sm+l m=1,2,..,M in Am=(2m-1-M0 1210g2 M 任意相邻两点之间的最小距离: M2-1 C bavg 最大相关度量判决规则 选择离最近的幅度电平为判决输出 ASK星座图中两种类型的点: 假设第m个信号点sm被发送 r=Sm+n M-2个内点一内点被发送时,当-5=川>2 时,发生错误 Ir-sm=nl =2]0急 2个外点一一外点的错误是内点错误概率的一半,因为噪声仅在一个方向上引起错误 2No
——内点被发送时,当 时,发生错误 4 选择离r最近的幅度电平为判决输出 带限信号传输的最佳检测和错误概率 ASK信号(M个一维信号点) m g Am s 2 1 = 任意相邻两点之间的最小距离: m =1, 2, …,M (2 1 ) A m M m = − − 2 min 2 12log 1 bavg M d M = − 最大相关度量判决规则 sm sm+1 sm-1 两相邻信号点 之间的距离: min d ASK星座图中两种类型的点: 2个外点 min min 0 2 2 2 ei d d P P n Q N = = M-2个内点 min 0 1 2 2 eo ei d P P Q N = = m r s n = + | | | | m r s n − = ——外点的错误是内点错误概率的一半,因为噪声仅在一个方向上引起错误 min 2 m d r s − min 2 − = m d r s n 假设第m个信号点sm被发送

带限信号传输的最佳检测和错误概率 符号的平均错误概率 P(crrori m sent) M M m=1 w-r】 代入dmin: 2- 610g2 M Ebanvg ≈20 610g2 M Ebavg M2-1N M2-1 No 5
5 符号的平均错误概率 1 min min 0 0 1 ( | ) 1 ( 2) 2 2 2 2 M e m P P error m sent M d d M Q Q M N N = = = − + 代入 dmin : 2 2 2 2 0 0 1 6log 6log 2(1 ) 2 1 1 bavg bavg e M M P Q Q M M N M N = − − − min 0 2( 1) 2 M d Q M N − = 带限信号传输的最佳检测和错误概率
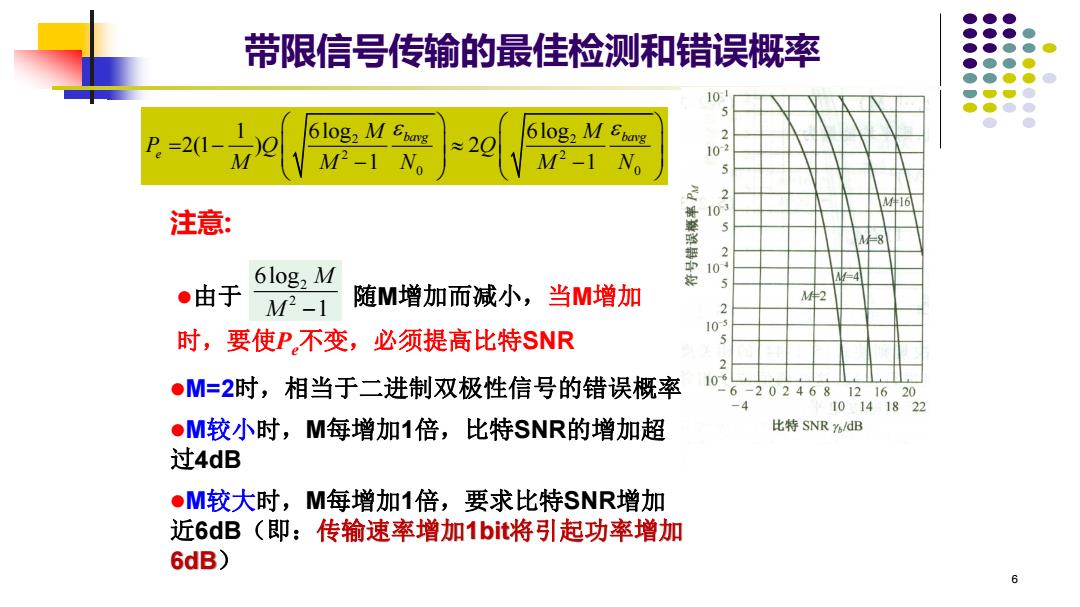
带限信号传输的最佳检测和错误概率 10 =-21-79 610g2 M Ebavg 2 MP-1N。 ≈2Q 610g2 M Ebavg M2-1N。 102 5 2 注意: 10 2 610g,M 10 4-4 ●由于 M2-1 随M增加而减小,当M增加 M件2 2 10 时,要使P不变,必须提高比特SNR ●M=2时,相当于二进制双极性信号的错误概率 109 6-202468 121620 10141822 ●M较小时,M每增加1倍,比特SNR的增加超 比特SNRa/dB 过4dB ●M较大时,M每增加1倍,要求比特SNR增加 近6dB(即:传输速率增加1bit将引起功率增加 6dB) 6
6 注意: ⚫由于 随M增加而减小,当M增加 时,要使Pe不变,必须提高比特SNR 带限信号传输的最佳检测和错误概率 2 2 6log 1 M M − 2 2 2 2 0 0 1 6log 6log 2(1 ) 2 1 1 bavg bavg e M M P Q Q M M N M N = − − − ⚫M=2时,相当于二进制双极性信号的错误概率 ⚫M较小时,M每增加1倍,比特SNR的增加超 过4dB ⚫M较大时,M每增加1倍,要求比特SNR增加 近6dB(即:传输速率增加1bit将引起功率增加 6dB)

4.3.2 PSK信号传输的最佳检测 和错误概率 7
7 4.3.2 PSK信号传输的最佳检测 和错误概率

带限信号传输的最佳检测和错误概率 PSK信号 信号波形 s.0=g0c0s21+2zm-月 1≤sM, 0≤K7 M 向量表达式 Sm= cos m-.sma- M 其中: 8= 28 一每个波形的能量 g(t)一发送信号的脉冲波形 将接收矢量r投影到M 最大相关度量判决准则 C(r,Sm) =r…Sm m=(1,2,.M) 个可能发送的信号矢 (等能量) 量上,再根据最大投 影分量判决发送信号 等价为 r的相位: 相关检测器 相位检测器 .tan- 计算接收信号r=(r1,r2)的相位,选择相位最接近的信号向量sm
计算接收信号 r=( r1 , r2 ) 的相位,选择相位最接近r的信号向量sm 8 向量表达式 ( 1)] 2 ( ) = ( ) cos[2 + m − M s t g t f t m c 信号波形 2 2 cos ( 1) , sin ( 1) m s m m M M = − − m m C(r,s ) = rs 1 1 2 tan r r r − = 1≤m≤M, 0≤t≤T 最大相关度量判决准则 m =(1,2,…M) 相关检测器 相位检测器 等价为 1 2 g 其中: = — 每个波形的能量 g( t ) — 发送信号的脉冲波形 (等能量) r 的相位: PSK信号 带限信号传输的最佳检测和错误概率 将接收矢量r投影到M 个可能发送的信号矢 量上,再根据最大投 影分量判决发送信号

带限信号传输的最佳检测和错误概率 问题 如何得到相位日,=tan12 的概率分布PDF? 再由此计算错误概率 等价为 r的相位: 相关检测器 相位检测器 =tanl 0 计算接收信号r=(r1,r2)的相位,选择相位最接近的信号向量sm
计算接收信号 r=( r1 , r2 ) 的相位,选择相位最接近r的信号向量sm 9 1 1 2 tan r r r − = 相关检测器 相位检测器 等价为 r 的相位: 带限信号传输的最佳检测和错误概率 如何得到相位 的概率分布PDF? 再由此计算错误概率 问题 1 1 2 tan r r r − =

带限信号传输的最佳检测和错误概率 相当于 假设:发送信号相位0=0 发送信号S1) 发送信号向量 s=[VE,0] 判决域为D: π 接收信号向量 r=3+n=[VE+%]=[55] 由于:n,n2一联合高斯随机变量→1 ,2也是联合高斯随机变量 E(r)=√E E(5)=0 联合PDF an=a=No/2=a2 P(,)= G-V2+ exp 问题:接收信号r 2πo 20; 的相位的PDF? 10
10 假设:发送信号相位 发送信号向量 = 0 r 1 s =[ , 0] : M M − 判决域为D1: 相当于 发送信号 s1 (t) 1 1 2 = + = + 接收信号向量 : r s n n n 1 E r( ) = ( ) 0 E r2 = 2 0 2 2 / 2 1 2 r = r = N = r 由于: n1 , n2 — 联合高斯随机变量 r1 , r2 也是联合高斯随机变量 联合PDF 2 2 1 2 1 2 2 2 1 ( ) ( , ) exp 2 2 r r r r r P r r − + = − 带限信号传输的最佳检测和错误概率 问题:接收信号r 的相位的PDF? = r r 1 2