
4.9 CPM信号的最佳接收机 ●CPM信号的最佳解调和检测 ●CPM信号的性能 1
1 4.9 CPM信号的最佳接收机 ⚫CPM信号的最佳解调和检测 ⚫CPM信号的性能

CPM信号的最佳接收机 CPM发送信号 s(t)= cos[2对t+(t,I)] 有记忆调制; 记忆来自相位连续性 接收信号 r(t)=s(t)+n(t) n(t)=n (t)cos2nft-n,(t)sin2nfi CPM信号的最佳接收机: 相关器 最大似然序列检测器 ●通过状态网格搜索最小欧氏距离的路径 ●采用Viterbi搜索算法 下面的工作: 1.建立CPM的状态网格结构 2.确定Viterbi)度量的计算 2
2 cos[2 ( , )] 2 ( ) f t t I T s t c = + CPM信号的最佳接收机 r(t) = s(t) + n(t) n t n t f t n t f t c c s 2 c ( ) = ( ) cos2 − ( )sin CPM发送信号 接收信号 CPM信号的最佳接收机: 相关器 最大似然序列检测器 ⚫通过状态网格搜索最小欧氏距离的路径 ⚫采用Viterbi搜索算法 下面的工作: 1. 建立CPM的状态网格结构 2. 确定Viterbi度量的计算 有记忆调制; 记忆来自相位连续性

CPM信号的最佳接收机 CPM的状态网格 CPM的状态一 每个信号间隔终了时载波相位的取值 CPM信号的载波相位(具有固定调制指数h时) t,)=2h∑Iqt-kT nT≤t≤(n+1)T k=- -L =πh∑1+2πh∑lqt-kT) k=-0 k=-L+1 =0n+0(t,) 式中: ()=g()d LT:信号脉冲g()的宽度 t1一一部分响应CPM 3
3 CPM的状态网格 0 ( ) ( ) 0 ( ) 0 1 ( ) 2 t q t g d t q t t LT q t = = = , , CPM信号的载波相位(具有固定调制指数h时) 式中: (t,I) 2 h I q(t kT) n k = k − =− LT:信号脉冲g(t)的宽度 L=1 —— 全响应CPM L>1 —— 部分响应CPM 1 2 ( ) n L n k k k k n L h I h I q t kT − =− = − + = + − ( , ) n = + t I CPM信号的最佳接收机 nT t n T + ( 1) t t LT g t = 0 ( ) 0 和 : CPM的状态 —— 每个信号间隔终了时载波相位的取值

CPM信号的最佳接收机 当h为有理数,h=m(m、p是互素的正整数) =00 ●m为偶数,有p个相位状态 ●m为奇数,有2p个相位状态 -cm 这时,仅由I决定下一个 ●L=1全响应CPM时,这些取值是网格图中唯一的状态; 状态迁移到何处 ●L>1部分响应时,还存在有附加的状态: t,I)=0n+0(t,) 部分响应附加的 相位状态: 0t,)=2h >Ig(t-kT)+2zhl,q(t-nT) k=n-L+l 0,0=2xh1t-kT) k=-L+1 相关状态向量 当前符号1的相位贡献 取决于信息符号{Un-1,n-2…LnL+} 表示相应于未达到最终值的 信号脉冲的相位项
4 2 ( 1) 0 s m m p m p p p − = , , ,K (2 1) 0 s m p m p p − = , ,K ( 2 ( ) 2 ( ) 1 1 t I h I q t k T h In q t n T n k n L = k − + − − = − + , ) 当 h为有理数,h=m/p (m、p是互素的正整数) ⚫m为偶数,有p个相位状态 ⚫m为奇数,有2p个相位状态 部分响应附加的 相位状态: ⚫L=1全响应CPM时,这些取值是网格图中唯一的状态; 相关状态向量 当前符号In的相位贡献 取决于信息符号{In-1 , In-2 , … In-L+1} 1 ( , ) 2 ( ) n k k n L t I h I q t kT = − + = − (t,I) (t,I) = n + CPM信号的最佳接收机 − =− = n L k n k h I ⚫L>1部分响应时,还存在有附加的状态: 表示相应于未达到最终值的 信号脉冲的相位项 这时,仅由In决定下一个 状态迁移到何处

CPM信号的最佳接收机 部分响应L>1时:CPM信号在=T时刻的状态可以表示为相位 状态和相关状态的组合。 S.=(0 I-1.In2.K I1) L-1个符号,有ML-1种组合 CPM总的状态数: PML- (偶数m) 当h=mp时: N.= 2PM- (奇数m) 假设仁nT时状态为Sn,则在t=(+l)T时,由于新符号的影响, 状态变为: S=(e.InIn1.K In-12) ,D=h21:+2xh立1,qt+k 其中: k=-0 k=刀-L十1 5
5 1 ( , ) 2 ( ) n L n k k k k n L t I h I h I q t kT − =− = − + = + + 1 2 1 ( ) S I I I n n n n n L = , − − − + , , K 1 1 1 2 ( ) S I I I n n n n n L + + − − + = , , , K n+1 = n +hIn−L+1 部分响应 L>1 时: CPM信号在t=nT 时刻的状态可以表示为相位 状态和相关状态的组合。 假设 t=nT 时状态为Sn,则在 t =(n+1)T 时,由于新符号的影响, 状态变为: 其中: 当 h=m/p 时: = − − 2 ( ) ( ) 1 1 PM m PM m N L L s 奇数 偶数 CPM总的状态数: L-1个符号,有ML-1种组合 n CPM信号的最佳接收机

CPM信号的最佳接收机 例:调制指数为h=3/4,L=2的部分响应脉冲的CPM =3 h=m )4 有28个相位状态日=+好++ 其中每个相位对应于两个相关状态(针对信号为1或-1) 总的状态数:N=16,即(0,1),(0,-1),(π,1)(π,-1) a,-,(-1 比如:相位状态8=一平且=-1,那么: 0n+1=On+πhln- π3π =一元 44 6
6 , 1) 4 3 , 1) ( 4 3 , 1) ( 2 1 , 1) ( 2 1 ( , 1) 4 1 , 1) ( 4 1 , 1) ( 4 3 , 1), ( 4 3 ( , 1) 2 1 , 1) ( 2 1 , 1) ( 4 1 , 1) ( 4 1 ( (0 1) (0 1) ( 1) ( , 1) − − − − − − − − − − − − − − , , , , , , , , , , 总的状态数:N=16,即 , , , , , , , 例:调制指数为h=3/4,L=2的部分响应脉冲的 CPM = , , , , 4 3 2 1 4 1 有 2p=8 个相位状态: s 0 比如:相位状态 且 ,那么: 7 ( ) 4 n = 1 1 = − n− I 1 1 3 4 4 + − = + = − − = − n n n hI 其中每个相位对应于两个相关状态(针对信号为1或 -1) CPM信号的最佳接收机 3 4 m h p = = 4 n = −
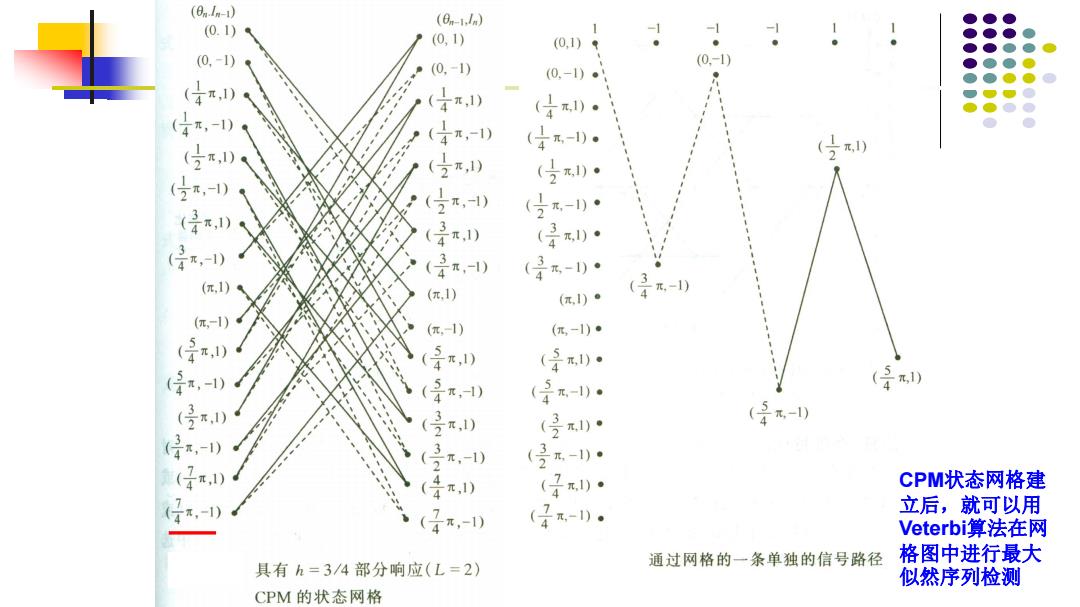
(0n.1n-) (6n-1.1n) (0.1) (0,1) (0,1) (0,-1) (0.-1) (0,-1) (0.-1)。 (,) /(, ()· (分, (,-0 (元-0。 (2π,1) (, (… ’(2,-10 (,1 (3元-)· 3 (年π,1) (是)· 3 ”(,-10 (-0… (π,1) (π1) (π1)● (π,-1) (π,1) (元,-1)· 5 (子π,) (2元)… 5 (元-… (元 八(子元,-) 、 3 (π,1) (2)· (5元-1) 4 3 元,- (2x-)… 4 (4π,1) (子)… CPM状态网格建 立后,就可以用 (4元,-1) Veterbi算法在网 格图中进行最大 具有h=3/4部分响应(L=2) 通过网格的一条单独的信号路径 似然序列检测 CPM的状态网格
7 CPM状态网格建 立后,就可以用 Veterbi算法在网 格图中进行最大 似然序列检测

CPM信号的最佳接收机 Viterbi算法中的度量计算 容易证明: 在特定发送符号序列I的条件下,观测信号(t)的对数概率与下列互 相关度量成正比: nTst≤(+1)T CM,(1)= "r(t)cos[ot+(,1]di (t,I)=0n+0(t,I) +1)7 CM(1)+ r(t)cos [@t+0+0(1,1)di CM(1)=[r(t)cos+]dt 直到nT时刻 在nT飞(n+1)T时间内的信号引起 幸存序列的度量 的度量的附加增量一V(I,On) 由于:{O}有P(或2P)个可能的相位状态, I=(LmLn,.InL+i,有M业个可能的符号序列 L个 所以:在每个信号间隔算出的V,(I,日n)有PM业(或2PM)个
8 CM I r t t t I dt n T n c + − = + ( 1) ( ) ( ) cos ( , ) Viterbi算法中的度量计算 在特定发送符号序列 I 的条件下,观测信号 r( t ) 的对数概率与下列互 相关度量成正比: 直到nT时刻 幸存序列的度量 在 nT≤t≤(n+1)T 时间内的信号引起 的度量的附加增量— Vn ( I, n ) 所以:在每个信号间隔算出的Vn ( I, θn ) 有 PML(或2PML)个。 ( 1) 1 ( ) ( ) cos ( , ) n T n c n nT CM I r t t t I dt + = + + + − 由于:{n } 有P(或2P)个可能的相位状态, I=(In , In-1 , … In-L+1), 有ML 个可能的符号序列 L个 (t,I) (t,I) = n + CM I r t t t I dt nT n c − − ( ) = ( ) cos + ( , ) 1 CPM信号的最佳接收机 容易证明: nT≤ t ≤(n+1)T

CPM信号的最佳接收机 Viterbi算法 ●对每一个状态,幸存序列数目是PM1(或2PML1)个 ●对每个幸存序列,有M个新的度量增量y,(I,O),它们附加 到现有度量上,产生PML(或2PM)个序列 ●在每个节点上,在汇合的M个序列中选取最有可能的序列, 舍弃其它M-1个序列,最终幸存序列的数目又回到PM1(或 2PML-1)个 9
9 Viterbi算法 ⚫对每一个状态,幸存序列数目是PML-1(或2PML-1)个 ⚫对每个幸存序列,有M个新的度量增量 vn ( I, n ),它们附加 到现有度量上,产生PML(或2PML)个序列 ⚫在每个节点上,在汇合的M个序列中选取最有可能的序列, 舍弃其它M-1个序列,最终幸存序列的数目又回到PML-1(或 2PML-1)个 CPM信号的最佳接收机

CPM信号的最佳接收机 CPM信号的性能 分析方法:在通过网格最小欧氏距离的路径基础上进行 假设:●相应两条相位轨迹的(:,I)和(1,I,)的两个信号为S和,S0 ●序列L和1的第一个符号不同 :0时刻分离,在后面 两条路径之间的距离与相应的信号有关: 某一时刻又重新汇合 在长度为T的间隔上,两条信号路径之间的欧氏距离定义为: dg=j兆(0-s,oFh 28 s(t) cos[ot+t,I)】 =20+s,2o)di-2s0s,0at -2Ns-2 coscosdr -2N-2"cos.1,),dr 2=1-eos6c,)-e,1}h 欧氏距离和相位差有关! 10
⚫相应两条相位轨迹的 和 的两个信号为Si (t) , Sj (t) ⚫序列 Ii 和 Ij 的第一个符号不同 t I t I dt 10 T NT = − i − j 0 1 cos ( , ) ( , ) 2 CPM信号的性能 分析方法:在通过网格最小欧氏距离的路径基础上进行 ( , ) i t I ( , ) j 假设: t I 在长度为 NT 的间隔上,两条信号路径之间的欧氏距离定义为: = − NT ij i j d s t s t dt 0 2 2 ( ) ( ) t I t I dt T N NT = − i − j 0 cos ( , ) ( , ) 2 2 t t I t t I dt T N c j NT c i cos ( , ) cos ( , ) 2 2 2 0 = − + + = + − NT i j NT j NT si t dt s t dt s t s t dt 0 0 2 0 2 ( ) ( ) 2 ( ) ( ) 欧氏距离和相位差有关! cos[ ( , )] 2 ( ) t t I T s t c = + CPM信号的最佳接收机 t=0时刻分离,在后面 某一时刻又重新汇合 两条路径之间的距离与相应的信号有关: